Участник:ArtyomKhakimov/Алгоритм Ланцоша для арифметики с плавающей точкой с выборочной ортогонализацией: различия между версиями
ASA (обсуждение | вклад) |
|||
| (не показана 21 промежуточная версия 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Assignment|ASA}} | ||
| + | |||
Авторы: Хакимов А. С. | Авторы: Хакимов А. С. | ||
| Строка 34: | Строка 36: | ||
== Математическое описание алгоритма == | == Математическое описание алгоритма == | ||
| − | <math> | + | На вход алгоритму поступает симметричная матрица math>A</math> и начальный вектор <math>b</math>. |
| − | + | ||
| − | + | Алгоритм вычисляет собственные вектора матрицы <math>T_k</math>, которые являются столбцами матрицы <math>Q_k V</math>. Матрица собственных значений <math>\Lambda</math>, где <math>V, \Lambda</math> из спектрального разложения <math>T_k = V\Lambda V^T</math>. При первой итерации вектор начального приближения <math>q_1 = \frac{b}{\|b\|_2}</math> нормируется. Затем задаются константы <math>\beta_0 = 0,\; q_0 = 0 </math>. | |
| − | + | ||
| − | + | Затем начинаются итерации алгоритма. Всего итераций не более <math>k</math>. В ходе итераций постепенно формируется матрица <math>T_k</math> из <math>\alpha_i</math>-x и <math>\beta_i</math>-х. | |
| − | + | ||
| − | + | Вычисления на <math>i</math>-й итерации таковы: | |
| − | + | Сначала вычисляется произведение матрицы на вектор <math>z = Aq_i</math>. Затем считается скалярное произведение <math>\alpha_i = q^T_i z</math> и значение сохраняется как элемент формируемой матрицы. После этого подизводится вычисление линейной комбинации векторов <math>z = z - \alpha_i q_i - \beta_{i-1}q_{i-1}</math>. Пусть норма полученного вектора - это элемент матрицы: <math>\beta_i = \|z\|_2</math>. Если <math>\beta_i</math> оказалась равной нулю, то итерации заканчиваются. Далее будет следовать этап вычисления собственных значений и собственных векторов. Иначе, в конце итерации считают <math>q_{i+1} = \frac{z}{\beta_i}</math> и переходят к следующей итерации. | |
| − | + | ||
| − | + | После всех итераций необходимо вычислить собственные значения и собственные вектора матрицы <math>T_k</math>.<ref>Деммель Д. Вычислительная линейная алгебра</ref> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Вычислительное ядро алгоритма == | == Вычислительное ядро алгоритма == | ||
| Строка 58: | Строка 55: | ||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| − | + | Алгоритма Ланцоша представляется в виде совокупности метода Ланцоша, построения крыловского подпространства и процедуры Рэлея-Ритца. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Каждая итерация первого этапа может быть разложена на следующие макроединицы: | |
| + | * Умножение матрицы на вектор | ||
| + | * Вычисление скалярного произведения векторов | ||
| + | * Умножение векторов на числа и вычитание векторов | ||
| + | * При выполнении условия необходимости переортогонализации – перемножение и вычитание векторов | ||
| + | * Вычисление нормы вектора | ||
| + | * Умножение вектора на число | ||
| − | + | Второй этап, процедура Рэлея-Ритца, заключается в нахождении собственных значений и собственных векторов матрицы и интерпретации их как приближенных значений собственных чисел и собственных векторов исходной матрицы, он может быть выполнен любым способом, например, QR-итерацией. | |
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| Строка 142: | Строка 131: | ||
<math>\mathsf{F}</math> — операция <math>z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i</math>, | <math>\mathsf{F}</math> — операция <math>z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i</math>, | ||
<math>\mathsf{f}</math> — вычисление линейной комбинации векторов | <math>\mathsf{f}</math> — вычисление линейной комбинации векторов | ||
| + | |||
| + | Информационный граф был построен на основе исходного кода программы, на нём указаны основные пути передачи информации между макроблоками алгоритма и между основными матричными и векторными операциями. | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| Строка 167: | Строка 158: | ||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| + | |||
| + | * Алгоритм устойчив, так как операция переортогонализации как раз направлена на исключение проблемы округления вычисляемых значений | ||
| + | * Вычислительная мощность алгоритма - отношение числа операций к суммарному объему входных и выходных данных - примерно равно <math>2k</math> | ||
| + | * При реализации классического алгоритма Ланцоша возникает большая погрешность при округлении. Вариант с полной переортогонализацией позволяет избегать больших погрешностей, однако является более ресурсоемким. Вариант с частичной переортогонализацией является промежуточным. | ||
| + | * Соотношение последовательной и параллельной сложности алгоритма равно <math>n</math>, что говорит о том, что параллельная реализация теоретически должна давать ощутимый выигрыш | ||
= Программная реализация = | = Программная реализация = | ||
| Строка 183: | Строка 179: | ||
*Число процессоров от 16 до 128. | *Число процессоров от 16 до 128. | ||
*Размерность матрицы от 5000 до 50000 с шагом 5000. | *Размерность матрицы от 5000 до 50000 с шагом 5000. | ||
| + | |||
| + | Использовался компилятор mpicxx в режиме openmpi/1.5.5-gcc. | ||
| + | Компиляция осуществлялась с параметрами по-умолчанию. | ||
| + | Запуск вычислений производился на узле regular4. | ||
{| class="wikitable" style="border: none; background: none;" | {| class="wikitable" style="border: none; background: none;" | ||
| Строка 223: | Строка 223: | ||
|} | |} | ||
| − | [[File: | + | По наклону графика при максимальной загрузке можно заметить, что на производительность алгоритма количество вычислительных процессов влияет сильнее, чем размерность входной матрицы. Наблюдается также ускорение при количестве параллельных процессоров 32 и размерности матрицы около 40 000 из чего можно сделать вывод, что такое сочетание является оптимальным для алгоритма Ланцоша. |
| + | |||
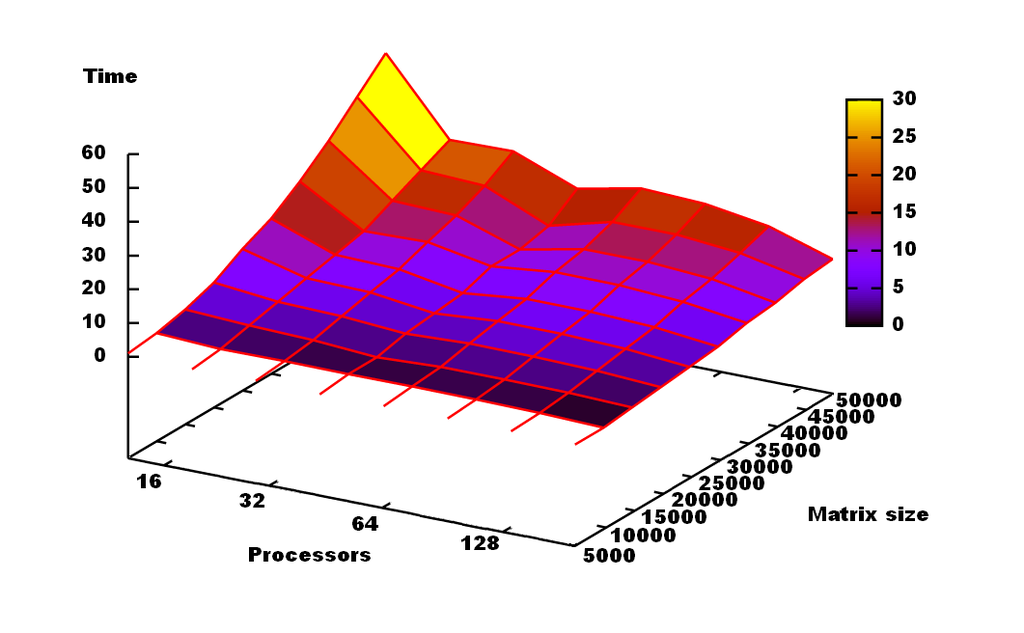
| + | [[File:Grph.PNG|1024px|center|рис. 2: Время работы алгоритма]] | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
Текущая версия на 14:10, 7 февраля 2017
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 07.02.2017 Данная работа соответствует формальным критериям. Проверено ASA. |
Авторы: Хакимов А. С.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм Ланцоша служит для нахождения собственных значений и собственных векторов для больших разреженных матриц, к которым нельзя применить прямые методы из-за больших требований к памяти и времени. Он был опубликован Корнелием Ланцошем в 1950 году. Его эффективность обусловлена экономией памяти для хранения матриц и экономией вычислительных ресурсов. Алгоритм итерационный и использует степенной метод для поиска наибольших собственных значений и векторов матриц. Основной недостаток алгоритма заключается в накоплении ошибок округления, для решения которых появились методы поддержания ортогонализации т.н. векторов Ланцоша. Здесь мы рассмотрим выборочный метод поддержания ортогонализации, который существенно экономит процессорное время.
На вход алгоритма подаётся [math]A = A^T[/math],
- [math] A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1\ n-1} & a_{1\ n} \\ a_{12} & a_{22} & a_{23} & \cdots & a_{2\ n-1} & a_{2\ n} \\ a_{13} & a_{23} & a_{33} & \cdots & a_{3\ n-1} & a_{3\ n} \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ a_{1\ n-1} & \cdots & \cdots & a_{n-2\ n-1} & a_{n-1\ n-1} & a_{n-1\ n} \\ a_{1\ n} & \cdots & \cdots & a_{n-2\ n} & a_{n-1\ n} & a_{n\ n} \\ \end{pmatrix} [/math] [math] ,\, \;[/math]
случайный вектор [math]b[/math], как первое приближение собственного вектора матрицы и [math]k [/math] - количество собственных значений и собственных векторов, которые требуется найти.
Матрица [math]Q_j = [q_1, q_2, \dots, q_j][/math] размерности [math]n \times j[/math] строится на каждой итерации и состоит из ортонормированных векторов Ланцоша. А в качестве приближенных собственных значений берутся числа Ритца [math]\theta_i [/math], - собственные значения симметричной трехдиагональной матрицы [math]T_j = Q^T_j A Q_j[/math] размерности [math]j \times j[/math].
- [math] T_j = \begin{pmatrix} \alpha_1 & \beta_1 \\ \beta_1 & \alpha_2 & \beta_2 \\ & \beta_2 & \ddots & \ddots \\ & & \ddots & \ddots & \beta_{j-1} \\ & & & \beta_{j-1} & \alpha_j \end{pmatrix}\; (2). [/math]
Однако, векторы [math]q_j [/math] теряют ортогональность вследствие приобретения больших компонент в направлениях векторов Ритца [math]y_{i,j} = Q_j v_i [/math], отвечающих сошедшимся числам Ритца [math] \theta_i [/math]. Поэтому чтобы построить [math]q_j [/math], предлагается на каждом шаге следить за оценками погрешностей [math]\beta_{t}|v_i(t)|, i = 1 \dots t, t = j - 1 [/math], где [math]v_i(t) [/math] - [math]t[/math]-я компонента собственного вектора [math]v_i [/math]. И когда какая-то оценка становится слишком малой, проводить ортогонализацию вектора Ланцоша [math]z [/math]. Величина [math]\beta_{t}|v_i(t)| [/math] считается малой, если она меньше, чем [math]\sqrt{\varepsilon}||T_{t}|| [/math], где [math]\varepsilon[/math] - доступная машинная точность чисел.
После следует вычисление собственных значений [math] \theta_j [/math] и собственных векторов [math]v_j [/math] полученной трехдиагональной матрицы [math]T_j[/math], например, с помощью метода "разделяй и властвуй"[1]
1.2 Математическое описание алгоритма
На вход алгоритму поступает симметричная матрица math>A</math> и начальный вектор [math]b[/math].
Алгоритм вычисляет собственные вектора матрицы [math]T_k[/math], которые являются столбцами матрицы [math]Q_k V[/math]. Матрица собственных значений [math]\Lambda[/math], где [math]V, \Lambda[/math] из спектрального разложения [math]T_k = V\Lambda V^T[/math]. При первой итерации вектор начального приближения [math]q_1 = \frac{b}{\|b\|_2}[/math] нормируется. Затем задаются константы [math]\beta_0 = 0,\; q_0 = 0 [/math].
Затем начинаются итерации алгоритма. Всего итераций не более [math]k[/math]. В ходе итераций постепенно формируется матрица [math]T_k[/math] из [math]\alpha_i[/math]-x и [math]\beta_i[/math]-х.
Вычисления на [math]i[/math]-й итерации таковы: Сначала вычисляется произведение матрицы на вектор [math]z = Aq_i[/math]. Затем считается скалярное произведение [math]\alpha_i = q^T_i z[/math] и значение сохраняется как элемент формируемой матрицы. После этого подизводится вычисление линейной комбинации векторов [math]z = z - \alpha_i q_i - \beta_{i-1}q_{i-1}[/math]. Пусть норма полученного вектора - это элемент матрицы: [math]\beta_i = \|z\|_2[/math]. Если [math]\beta_i[/math] оказалась равной нулю, то итерации заканчиваются. Далее будет следовать этап вычисления собственных значений и собственных векторов. Иначе, в конце итерации считают [math]q_{i+1} = \frac{z}{\beta_i}[/math] и переходят к следующей итерации.
После всех итераций необходимо вычислить собственные значения и собственные вектора матрицы [math]T_k[/math].[2]
1.3 Вычислительное ядро алгоритма
- Умножение матрицы на вектор, [math]z=Aq_j, [/math].
- Ортогонализация по отношению к сошедшимся векторам [math]z = z-(y^T_{i,k},z)y_{i,k} [/math] для [math]i = 1 \dots t[/math]
1.4 Макроструктура алгоритма
Алгоритма Ланцоша представляется в виде совокупности метода Ланцоша, построения крыловского подпространства и процедуры Рэлея-Ритца.
Каждая итерация первого этапа может быть разложена на следующие макроединицы:
- Умножение матрицы на вектор
- Вычисление скалярного произведения векторов
- Умножение векторов на числа и вычитание векторов
- При выполнении условия необходимости переортогонализации – перемножение и вычитание векторов
- Вычисление нормы вектора
- Умножение вектора на число
Второй этап, процедура Рэлея-Ритца, заключается в нахождении собственных значений и собственных векторов матрицы и интерпретации их как приближенных значений собственных чисел и собственных векторов исходной матрицы, он может быть выполнен любым способом, например, QR-итерацией.
1.5 Схема реализации последовательного алгоритма
Алгоритм выполняется в следующей последовательности:
[math]1.\, \, \beta_0 = 0,\; q_0 = 0[/math] #Инициализируем векторы [math]2.\, \, \|b\|_2 = \sqrt{\sum\limits_{j=1}^{n} b_j^2}[/math] #Вычисляем норму вектора начального приближения. [math]3.\, \, q_{1_{j}} = \frac{b_{j}}{\|b\|_2}, \; j = 1,\, \dots\,, n[/math] #Нормализуем вектор начального приближения. [math]4.\, \,[/math] Начинается цикл, в котором не более чем [math]k[/math]. На [math]i[/math]-й итерации производятся следующие вычисления: [math]4.1.\, \, z_j = \sum\limits_{m=1}^{n} a_{jm} q_{i_m}, \; j = 1,\,\dots\,, n[/math] #Считаем результат применения линейного оператора [math]A[/math] к вектору [math]q_i[/math]. [math]4.2.\, \, \alpha_i = \sum\limits_{j=1}^{n}q_{i_j} z_j[/math] #Получаем результат скалярного произведения векторов [math]q_i[/math] и [math]z[/math]. [math]4.3.\, \, z_j = z_j - \alpha_i q_{i_j} - \beta_{i-1}q_{i-1_j}, \, j = 1,\,\dots\,, n[/math] #Вычисляем линейную комбинацию векторов. [math]4.4.\, \,[/math] Начинается цикл, в котором производится выборочная ортогонализация векторов Ланцоша [math]4.4.1.\, \,[/math] Вычисляется вектор Ритца [math]y_{i,k_d} = \sum\limits_{x=1}^{k} q_{x_d} v_{i_x}, \; d = 1,\,\dots\,, n,[/math], где [math]y_{i,k_d}[/math] - [math]d[/math]-я компонента вектора Ритца [math]y,[/math] [math]4.4.2.\, \,[/math] Производится скалярное умножение [math]y_{i,k}^T[/math] и [math] z: \; \; \gamma = \sum\limits_{d=1}^{n}y_{i,k_d} z_d,[/math] [math]4.4.3.\, \,[/math] Ищется новое собственное значение [math] \theta_j [/math] и собственный вектор [math] v_j [/math] для полученной матрицы [math] T_j,[/math] [math]4.5.\, \, \beta_i = \|z\|_2 = \sqrt{\sum\limits_{j=1}^{n} z_j^2}[/math] #Считаем норму вектора [math]z[/math]. [math]4.6.[/math] Проверка равенства [math]\beta_i == 0[/math] # Если норма оказалась равной нулю, то завершаем итерации и переходим к вычислению собственных векторов и собственных значений полученной матрицы. В обратном случае, продолжаем выполнения итераций. [math]4.7.\, \, q_{i+1_j} = \frac{z_j}{\beta_i}, \; j = 1,\, \dots \,, n[/math] #Нормируем вектор [math]z[/math]. [math]4.8.\,[/math] Если выполнили [math]k[/math] итераций, то завершаем выполнение итераций, переходим к следующему шагу. Иначе начинаем последующую итерацию цикла. [math]5.[/math] Вычисляем собственные значения и собственные вектора полученной матрицы [math]T_k[/math].
1.6 Последовательная сложность алгоритма
- Вычисление вектора [math]z[/math] - [math]n^2[/math] операций умножения и [math]n(n-1)[/math] операций сложения
- Вычисление скалярного произведения векторов - [math]n[/math] операций умножения и [math](n-1)[/math] сложений
- Вычисление вектора [math]z[/math] - [math]2n[/math] умножений и [math]2n[/math] сложений
- Оценка погрешностей - [math]kn[/math] операций умножения
- Выборочная переортогонализация - [math]O(2nj)[/math] умножений и [math]O(2j(n-1) + n)[/math] сложений
- Вычисление нормы вектора - [math]n[/math] операций умножения и [math](n-1)[/math] сложений
- Вычисление нового столбца матрицы [math]Q[/math] - [math]n[/math] операций умножения
Итого на каждой итерации:
- Умножений: [math]n^2 + n + 2n + kn + O(2nj) + n + n = n^2 + 5n + kn + O(2nj)[/math]
- Сложений: [math]n(n-1) + n-1 + 2n + O(2j(n-1) + n) + n-1 = n^2 + 3n + O(2j(n-1) + n) -2[/math]
Итого за все время выполнения алгоритма:
- Умножений: [math]kn^2 + 5kn + k^2n + O(k^2n + kn)[/math]
- Сложений: [math]kn^2 + 3kn + O((k^2+k)(n-1)+kn) = kn^2 + 3kn + O(k^2(n-1)+2kn-k)[/math]
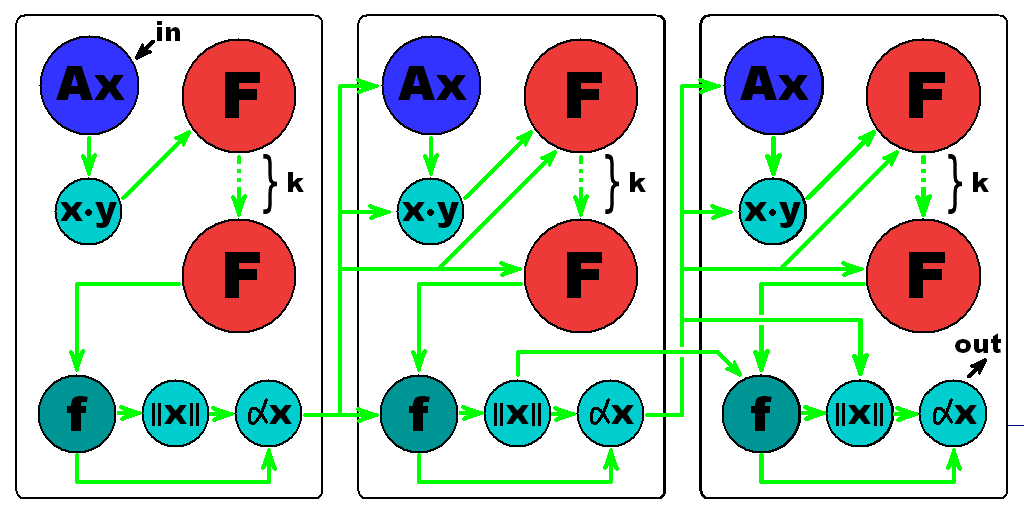
1.7 Информационный граф
Здесь: [math]Ax[/math] — перемножение матрицы и вектора, [math]\|x\|[/math] — макрооперация взятия нормы, [math]\alpha x[/math] — умножение скаляра на вектор, [math]\cdot [/math] — операция скалярного умножения векторов, [math]\mathsf{F}[/math] — операция [math]z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i[/math], [math]\mathsf{f}[/math] — вычисление линейной комбинации векторов
Информационный граф был построен на основе исходного кода программы, на нём указаны основные пути передачи информации между макроблоками алгоритма и между основными матричными и векторными операциями.
1.8 Ресурс параллелизма алгоритма
На каждой из итераций алгоритма можно получить выигрыш за счет распараллеливания следующих шагов:
- Вычисление вектора [math]z[/math] - умножение матрицы размера [math]n \times n[/math] на вектор длины [math]n[/math] - [math]n[/math] ярусов сложений, [math]n[/math] операций умножений в каждом
- Вычисление коэффициента [math]\alpha_j[/math] - скалярное произведение векторов - [math]n[/math] ярусов сложений, 1 операция умножения в каждом
- Вычисление нового значения вектора [math]z[/math]: 2 яруса умножений длины [math]n[/math] (умножение вектора на число), 2 яруса вычитаний длины [math]n[/math]
- Выборочная переортогонализация: последовательно для всех [math]i \le k[/math] выполняется [math]j[/math] ярусов сложений, [math]n[/math] операций умножений в каждом, [math]n[/math] ярусов сложений, [math]j[/math] операций умножений в каждом, один ярус вычитаний размера [math]n[/math]
- Вычисление [math]\beta_j[/math] - скалярное произведение векторов - [math]n[/math] ярусов сложений, 1 операция умножения в каждом
- Вычисление [math]q_j[/math] - деление вектора на число - один ярус делений размера [math]n[/math]
Сложность алгоритма по ширине ЯПФ - [math]O(n)[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: вещественная матрица [math]A[/math] размера [math]n \times n[/math], вектор [math]b[/math] длины [math]n[/math], число [math]k[/math]
Объем входных данных: [math]n^2 + n + 1[/math]
Выходные данные: матрица [math]Q[/math] размера [math]n \times k[/math]
Объем выходных данных: [math]nk[/math]
1.10 Свойства алгоритма
- Алгоритм устойчив, так как операция переортогонализации как раз направлена на исключение проблемы округления вычисляемых значений
- Вычислительная мощность алгоритма - отношение числа операций к суммарному объему входных и выходных данных - примерно равно [math]2k[/math]
- При реализации классического алгоритма Ланцоша возникает большая погрешность при округлении. Вариант с полной переортогонализацией позволяет избегать больших погрешностей, однако является более ресурсоемким. Вариант с частичной переортогонализацией является промежуточным.
- Соотношение последовательной и параллельной сложности алгоритма равно [math]n[/math], что говорит о том, что параллельная реализация теоретически должна давать ощутимый выигрыш
2 Программная реализация
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование алгоритма на масштабируемость производилось на суперкомпьютере "Ломоносов" с использованием технологии MPI. Для тестирования была выбрана вот эта реализация алгоритма.
Набор параметров, которые изменялись при тестировании:
- Число процессоров от 16 до 128.
- Размерность матрицы от 5000 до 50000 с шагом 5000.
Использовался компилятор mpicxx в режиме openmpi/1.5.5-gcc. Компиляция осуществлялась с параметрами по-умолчанию. Запуск вычислений производился на узле regular4.
| Число процессоров | |||||
|---|---|---|---|---|---|
| 16 | 32 | 64 | 128 | ||
| Размер матрицы | 5000 | 1,07 | 0,71 | 0,62 | 0,54 |
| 10000 | 2,39 | 1,94 | 1,17 | 0,79 | |
| 15000 | 4,35 | 3,38 | 1,89 | 1,59 | |
| 20000 | 7,63 | 5,19 | 3,78 | 2,35 | |
| 15000 | 12,41 | 7,33 | 4,32 | 3,44 | |
| 30000 | 16,68 | 9,36 | 5,02 | 4,68 | |
| 35000 | 22,58 | 11,92 | 8,04 | 6,20 | |
| 40000 | 29,31 | 15,90 | 8,47 | 7,43 | |
| 45000 | 37,04 | 19,42 | 10,55 | 9,04 | |
| 50000 | 45,64 | 23,39 | 16,09 | 10,25 | |
По наклону графика при максимальной загрузке можно заметить, что на производительность алгоритма количество вычислительных процессов влияет сильнее, чем размерность входной матрицы. Наблюдается также ускорение при количестве параллельных процессоров 32 и размерности матрицы около 40 000 из чего можно сделать вывод, что такое сочетание является оптимальным для алгоритма Ланцоша.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации
Реализация в проекте Vienna VL[3]
Реализация в проекте IETL[4]
Реализация в проекте ARPACK [5]
Lanczos Plus Plus [6]
ED Lanczos [7]
Paralleles Rechnen 2 [8]
Cuda-Arnoldi [9]
3 Литература
- ↑ Дж. Деммель «Вычислительная линейная алгебра», c. 232, алгоритм 5.2
- ↑ Деммель Д. Вычислительная линейная алгебра
- ↑ https://github.com/viennacl/viennacl-dev
- ↑ http://www.comp-phys.org/software/ietl/lanczos.html
- ↑ http://www.caam.rice.edu/software/ARPACK/
- ↑ https://github.com/g1257/LanczosPlusPlus
- ↑ https://github.com/henhans/ED_lanczos
- ↑ https://github.com/soneyworld/ParallelesRechnen2
- ↑ https://github.com/trantalaiho/Cuda-Arnoldi/