Участник:Антонина Егорова/Алгоритм кластеризации категориальных данных CLOPE: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
 
(не показано 6 промежуточных версий этого же участника)
Строка 5: Строка 5:
  
 
=== Математическое описание алгоритма ===
 
=== Математическое описание алгоритма ===
 +
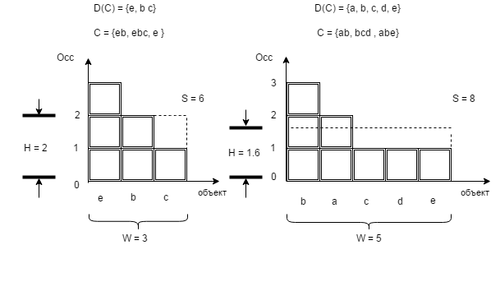
[[Файл:clope.png|500px|thumb|right|Разбиение набора транзакций на два кластера.]]
 +
 
Пусть имеется база транзакций <math>D</math>, которая состоит из множества транзакций <math>\{t_1,t_2,...,t_n\}</math>. При этом каждая транзакция - набор объектов <math>\{i_1,...,i_m\} </math>.  
 
Пусть имеется база транзакций <math>D</math>, которая состоит из множества транзакций <math>\{t_1,t_2,...,t_n\}</math>. При этом каждая транзакция - набор объектов <math>\{i_1,...,i_m\} </math>.  
  
Строка 33: Строка 35:
  
 
Таким образом задача кластеризации алгоритмом CLOPE состоит в том, чтобы для заданных множества <math>D</math> и коэффициента отталкивания <math>r</math> найти такое разбиение <math>C</math>, для которого значение функции цены максимально.
 
Таким образом задача кластеризации алгоритмом CLOPE состоит в том, чтобы для заданных множества <math>D</math> и коэффициента отталкивания <math>r</math> найти такое разбиение <math>C</math>, для которого значение функции цены максимально.
−
 
−
 
 
Постановка задачи кластеризации алгоритмом CLOPE выглядит следующим образом:  
 
Постановка задачи кластеризации алгоритмом CLOPE выглядит следующим образом:  
  
 
для заданных <math>D</math> и <math>r</math> найти разбиение <math>C</math> такое, что:  
 
для заданных <math>D</math> и <math>r</math> найти разбиение <math>C</math> такое, что:  
−
<math>Profit(C) \longrightarrow max </math>.
+
<math>Profit(C) \longrightarrow max </math>.<ref>
 +
Yang, Y., Guan, H., You. J. CLOPE: A fast and Effective Clustering Algorithm for Transactional Data In Proc. of SIGKDD’02, July 23-26, 2002, Edmonton, Alberta, Canada.</ref>
  
 
=== Вычислительное ядро алгоритма ===
 
=== Вычислительное ядро алгоритма ===
Строка 47: Строка 48:
 
*<math>W_{new}(C_i)=\mid D(C_i \cup t_n)|</math>
 
*<math>W_{new}(C_i)=\mid D(C_i \cup t_n)|</math>
  
−
*вычисление стоимости <math>\frac{S_{new}(C_i)(\mid C_i \mid \pm 1)}{W_{new}(C_i)^r} - \frac{S(C_i) \mid C_i \mid }{W(C_i)^r}</math>
+
*вычисление стоимости добавления(удаления)<math>\frac{S_{new}(C_i)(\mid C_i \mid \pm 1)}{W_{new}(C_i)^r} - \frac{S(C_i) \mid C_i \mid }{W(C_i)^r}</math>
  
 
=== Макроструктура алгоритма ===
 
=== Макроструктура алгоритма ===
Строка 54: Строка 55:
 
=== Схема реализации последовательного алгоритма ===
 
=== Схема реализации последовательного алгоритма ===
  
 +
<ol>
 +
<li>Инициализация. Последовательно для каждой транзакции считается цена добавления ко всем существующим или новому пустому кластерам. В результате, транзакция занимает место в том кластере, для которого цена добавления максимальна(если это пустой кластер, то необходимо его создать). В конечном итоге все транзакции будут находиться в кластерах.</li>
 +
<li>Итерации. Этот этап нужен для возможного улучшения результата, полученного на первом шаге. При этом для каждой транзакции вычисляется стоимость удаления из кластера, в котором она находится, и цена добавления в каждый существующий или пустой кластер. Необходимо посчитать и найти максимальную суммарную стоимость удаления и добавления транзакции к каждому кластеру. Если максимальная стоимость положительная, то данная транзакция перемещается в этот кластер. Это выполняется для каждой транзакции.
 +
Итерация повторяется до тех пор, пока результат улучшается. Как только за итерацию ничего не меняется, алгоритм заканчивает работу. </li>
 +
</ol>
  
 
==== Описание реализации алгоритма на псевдокоде ====
 
==== Описание реализации алгоритма на псевдокоде ====
 +
Вход:
 +
    <math>t</math> - транзакции,
 +
    <math>r</math> - коэффициент отталкивания
 +
 +
Выход:
 +
    <math>C</math> - множество кластеров
 +
 +
'''инициализация:'''
 +
  '''while ''' не конец '''do'''
 +
      '''read''' следующую транзакцию <math>t</math>
 +
      определить существующий кластер или пустой <math>C_j</math>, который дает максимум функции стоимости <math>Profit</math>
 +
      '''write''' транзакцию в кластер <math>C_j</math>
 +
  '''end while'''
 +
 +
'''итерация''':
 +
    '''repeat'''
 +
        в начало таблицы транзакций
 +
        change = false
 +
        '''while''' не конец таблицы '''do'''
 +
          '''read''' следующую транзакцию <math>t_i</math> из таблицы
 +
          sum_max = 0
 +
          '''for''' для каждого кластера <math>C_j</math>
 +
              вычислить сумму <math>Sum</math> стоимости удаления из кластера <math>C_i</math> и добавления транзакции к <math>C_j</math>(j<>i)
 +
              '''if'''  Sum > sum_max '''then'''
 +
                    sum_max = Sum
 +
                    запомнить номер кластера <math>l</math>
 +
              '''end if'''
 +
          '''end for'''
 +
          '''if''' sum_max>0 
 +
              change = true
 +
              '''write''' транзакцию <math>t_i</math> в кластер <math>C_l</math>, который максимизирует функцию цены
 +
          '''end if'''
 +
        '''end while'''
 +
    '''until''' not change
 +
    '''delete''' все пустые кластеры
  
 
=== Последовательная сложность алгоритма ===
 
=== Последовательная сложность алгоритма ===
 +
Пусть <math>n</math> - количество транзакций, <math>m</math> - максимальное количество объектов транзакции, <math>k</math> - количество кластеров.
 +
 +
На каждой итерации для одной транзакции основные вычисления выполняются в функции добавления и удаления транзакции из кластера : производится 1 сложение, не более <math>m</math> сложений/вычитаний, 2 умножения, 2 деления, 2 возведения в степень и 1 сложение - итого <math>m + 8</math> операций.
 +
 +
Операции выполняются для всех транзакций (<math>n</math> штук) и для всех кластеров (<math>k</math> штук). Итого выполняется <math>n*k*(m+8)</math> операций.
 +
 +
Помимо этого при удалении транзакции к кластеру производится пересчет его характеристик: <math>m+2</math> операции.
  
 +
Сложность алгоритма равна <math>O(n*k*m)</math>.
 
=== Информационный граф ===
 
=== Информационный граф ===
 +
 +
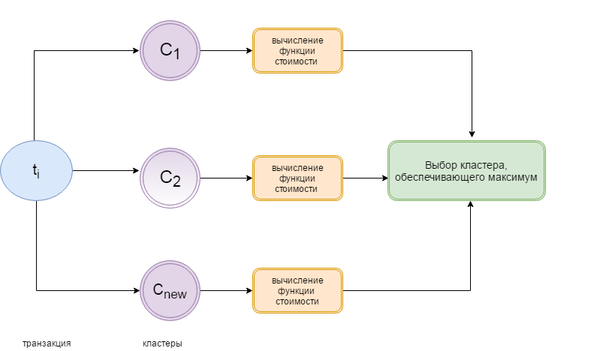
На этапе итерации для любой транзакции функции стоимости удаления и добавления могут работать параллельно для каждого кластера.
 +
[[Файл:iter.png ‎|600px|center|Итерации]]
 +
  
 
=== Ресурс параллелизма алгоритма ===
 
=== Ресурс параллелизма алгоритма ===
 +
 +
Вычисления стоимости добавления и удаления транзакции выполняются независимо для всех кластеров. Именно поэтому все такие вычисления  для одной транзакции можно производить параллельно. Таким образом, сложность алгоритма с <math>O(n*k*m)</math> понижается до <math>O(n*m)</math>, где <math>k</math> - количество кластеров.
  
 
=== Входные и выходные данные алгоритма ===
 
=== Входные и выходные данные алгоритма ===
 +
'''Входные данные:'''
 +
 +
<math>n</math> транзакций максимальной длины <math>m</math> и коэффициент отталкивания <math>r</math>.
 +
 +
'''Выходные данные:'''
 +
 +
Распределение транзакции по кластерам в соответствии с кластеризацией(числовая последовательность длины <math>n</math>).
  
 
=== Свойства алгоритма ===
 
=== Свойства алгоритма ===
  
 +
* Алгоритм не устойчив, так как результат его работы зависит от порядка считывания транзакций и текущего набора кластеров.
 +
* Алгоритм не детерминирован , так как результат алгоритма зависит от порядка считывания транзакций.
 +
Если множество транзакций представить в виде пронумерованного списка, то результат будет однозначным.
 +
* Количество кластеров определяет отношение последовательной и параллельной сложности алгоритма : <math>\dfrac{O(n*m*k)}{O(n*m)} = k</math>
 +
* Быстро работает для большого количества категориальных данных, так как в оперативной памяти необходимо хранить небольшое количество информации по каждому кластеру и требуется минимальное число сканирований набора транзакций. <ref>Н. Паклин. «Кластеризация категорийных данных: масштабируемый алгоритм CLOPE». Электронное издание. http://www.basegroup.ru/clusterization/clope.htm </ref>
 +
*Вычислительная мощность операций алгоритма: <math>\frac{O(N*k*A)}{N*A + N + 1} = O(k)</math>.
 
== Программная реализация алгоритма ==
 
== Программная реализация алгоритма ==
  
Строка 82: Строка 150:
  
 
=== Существующие реализации алгоритма ===
 
=== Существующие реализации алгоритма ===
 +
Первое описание данного алгоритма появилось совсем недавно, этим можно объяснить небольшое количество его реализаций.
 +
* http://weka.sourceforge.net/doc.stable/weka/clusterers/CLOPE.html - реализация в open source библиотеке для анализа данных WEKA(Waikato Environment for Knowledge Analysis) на языке Java
 +
Помимо этого существуют пользовательские реализации алгоритма:
 +
* https://github.com/infozor/php_mysql_clustering_clope - реализация алгоритма на PHP
 +
* https://github.com/Tolsi/scala-clope - реализация алгоритма Scala
 +
  
 
== Литература ==
 
== Литература ==
−
 
 
<references \>
 
<references \>

Текущая версия на 11:37, 6 февраля 2017

Содержание

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм CLOPE (Clustering with sLOPE) предназначен для кластеризации огромных наборов категориальных данных. В основе данного алгоритма лежит идея максимизации глобальной функции стоимости, повышающей близость транзакций в кластерах при помощи увеличения параметра кластерной гистограммы. Во время работы этого алгоритма в оперативной памяти хранится только текущая транзакция и немного информации по каждому кластеру.

1.2 Математическое описание алгоритма

Разбиение набора транзакций на два кластера.

Пусть имеется база транзакций [math]D[/math], которая состоит из множества транзакций [math]\{t_1,t_2,...,t_n\}[/math]. При этом каждая транзакция - набор объектов [math]\{i_1,...,i_m\} [/math].

Множество кластеров [math]\{C_1,...,C_k\} [/math] - это разбиение множества транзакций [math]\{t_1,...t_n\} [/math], при котором

  1. [math]C_1 \cup \ldots \cup C_k = \{t_1,...,t_n\}[/math]
  2. [math]C_i[/math] [math]\ne[/math] [math]\empty[/math] [math]\land[/math] [math]C_i[/math] [math]\cap[/math] [math]C_j= \empty[/math], для [math]1[/math] [math]\le[/math] [math]i[/math], [math] j[/math] [math] \le[/math] [math] k[/math].

Для каждого кластера [math]C[/math] определяются следующие характеристики :

[math]D(C)[/math] — множество уникальных объектов в данном кластере [math] C[/math],
[math]Occ(i,C) [/math] — количество вхождений объекта [math] i[/math] в кластер [math] C[/math] ,
[math]S(C) = \sum_{i \in D(C)} Occ(i,C) = \sum _{t_i \in C} \mid t_i \mid [/math]; — количество всех объектов в кластере [math] C[/math],
[math]W(C) [/math]  =  [math] \mid[/math] [math]D(C)[/math] [math]\mid[/math] — ширина кластера,
[math]H(C)[/math]  =  [math] \frac{S(C)}{W(C)}[/math] — высота кластера.

Функция стоимости:

[math] Profit(C) = \frac{\sum^{k}_{i=1} \frac{S(C_i)}{W(C_i)^r} \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid } [/math],

где [math]\mid C_i \mid[/math] - количество объектов в [math]i[/math]-ом кластере, [math]k[/math] – общее количество кластеров. Коэффициент отталкивания [math]r[/math] регулирует уровень похожести среди транзакций одного кластера. Чем больше [math]r[/math], тем ниже уровень сходства и тем больше кластеров будет сгенерировано.

Таким образом задача кластеризации алгоритмом CLOPE состоит в том, чтобы для заданных множества [math]D[/math] и коэффициента отталкивания [math]r[/math] найти такое разбиение [math]C[/math], для которого значение функции цены максимально. Постановка задачи кластеризации алгоритмом CLOPE выглядит следующим образом:

для заданных [math]D[/math] и [math]r[/math] найти разбиение [math]C[/math] такое, что: [math]Profit(C) \longrightarrow max [/math].[1]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма заключается в том, чтобы вычислять цену добавления и цену удаления транзакции из кластера на каждом шаге. Для этого необходимо найти результат следующих операций:

  • [math]S_{new}(C_i)=S(C_i) \pm \mid(t_n)\mid [/math],
  • [math]W_{new}(C_i)=\mid D(C_i \cup t_n)|[/math]
  • вычисление стоимости добавления(удаления)[math]\frac{S_{new}(C_i)(\mid C_i \mid \pm 1)}{W_{new}(C_i)^r} - \frac{S(C_i) \mid C_i \mid }{W(C_i)^r}[/math]

1.4 Макроструктура алгоритма

Алгоритм состоит из двух этапов - инициализации и итерации. На первом этапе создается исходное разбиение - считываются все транзакции, которые помещаются в определенные кластеры, определяющиеся максимизацией функции стоимости. Второй этап может повторяться несколько раз до тех пор, пока перемещение транзакции в другой кластер не увеличивает функцию стоимости.

1.5 Схема реализации последовательного алгоритма

  1. Инициализация. Последовательно для каждой транзакции считается цена добавления ко всем существующим или новому пустому кластерам. В результате, транзакция занимает место в том кластере, для которого цена добавления максимальна(если это пустой кластер, то необходимо его создать). В конечном итоге все транзакции будут находиться в кластерах.
  2. Итерации. Этот этап нужен для возможного улучшения результата, полученного на первом шаге. При этом для каждой транзакции вычисляется стоимость удаления из кластера, в котором она находится, и цена добавления в каждый существующий или пустой кластер. Необходимо посчитать и найти максимальную суммарную стоимость удаления и добавления транзакции к каждому кластеру. Если максимальная стоимость положительная, то данная транзакция перемещается в этот кластер. Это выполняется для каждой транзакции. Итерация повторяется до тех пор, пока результат улучшается. Как только за итерацию ничего не меняется, алгоритм заканчивает работу.

1.5.1 Описание реализации алгоритма на псевдокоде

Вход: 

    [math]t[/math] - транзакции,
    [math]r[/math] - коэффициент отталкивания

Выход: 

    [math]C[/math] - множество кластеров

инициализация: 

  while  не конец do
      read следующую транзакцию [math]t[/math]
      определить существующий кластер или пустой [math]C_j[/math], который дает максимум функции стоимости [math]Profit[/math]
      write транзакцию в кластер [math]C_j[/math]
  end while

итерация: 

    repeat
       в начало таблицы транзакций
       change = false
       while не конец таблицы do
          read следующую транзакцию [math]t_i[/math] из таблицы
          sum_max = 0
          for для каждого кластера [math]C_j[/math]
             вычислить сумму [math]Sum[/math] стоимости удаления из кластера [math]C_i[/math] и добавления транзакции к [math]C_j[/math](j<>i)
             if  Sum > sum_max then
                   sum_max = Sum 
                   запомнить номер кластера [math]l[/math] 
             end if
          end for
          if sum_max>0  
             change = true
             write транзакцию [math]t_i[/math] в кластер [math]C_l[/math], который максимизирует функцию цены
          end if
       end while
    until not change
    delete все пустые кластеры

1.6 Последовательная сложность алгоритма

Пусть [math]n[/math] - количество транзакций, [math]m[/math] - максимальное количество объектов транзакции, [math]k[/math] - количество кластеров.

На каждой итерации для одной транзакции основные вычисления выполняются в функции добавления и удаления транзакции из кластера : производится 1 сложение, не более [math]m[/math] сложений/вычитаний, 2 умножения, 2 деления, 2 возведения в степень и 1 сложение - итого [math]m + 8[/math] операций.

Операции выполняются для всех транзакций ([math]n[/math] штук) и для всех кластеров ([math]k[/math] штук). Итого выполняется [math]n*k*(m+8)[/math] операций.

Помимо этого при удалении транзакции к кластеру производится пересчет его характеристик: [math]m+2[/math] операции.

Сложность алгоритма равна [math]O(n*k*m)[/math].

1.7 Информационный граф

На этапе итерации для любой транзакции функции стоимости удаления и добавления могут работать параллельно для каждого кластера.

Итерации


1.8 Ресурс параллелизма алгоритма

Вычисления стоимости добавления и удаления транзакции выполняются независимо для всех кластеров. Именно поэтому все такие вычисления для одной транзакции можно производить параллельно. Таким образом, сложность алгоритма с [math]O(n*k*m)[/math] понижается до [math]O(n*m)[/math], где [math]k[/math] - количество кластеров.

1.9 Входные и выходные данные алгоритма

Входные данные:

[math]n[/math] транзакций максимальной длины [math]m[/math] и коэффициент отталкивания [math]r[/math].

Выходные данные:

Распределение транзакции по кластерам в соответствии с кластеризацией(числовая последовательность длины [math]n[/math]).

1.10 Свойства алгоритма

  • Алгоритм не устойчив, так как результат его работы зависит от порядка считывания транзакций и текущего набора кластеров.
  • Алгоритм не детерминирован , так как результат алгоритма зависит от порядка считывания транзакций.

Если множество транзакций представить в виде пронумерованного списка, то результат будет однозначным.

  • Количество кластеров определяет отношение последовательной и параллельной сложности алгоритма : [math]\dfrac{O(n*m*k)}{O(n*m)} = k[/math]
  • Быстро работает для большого количества категориальных данных, так как в оперативной памяти необходимо хранить небольшое количество информации по каждому кластеру и требуется минимальное число сканирований набора транзакций. [2]
  • Вычислительная мощность операций алгоритма: [math]\frac{O(N*k*A)}{N*A + N + 1} = O(k)[/math].

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Первое описание данного алгоритма появилось совсем недавно, этим можно объяснить небольшое количество его реализаций.

Помимо этого существуют пользовательские реализации алгоритма:


3 Литература

<references \>

  1. ↑ Yang, Y., Guan, H., You. J. CLOPE: A fast and Effective Clustering Algorithm for Transactional Data In Proc. of SIGKDD’02, July 23-26, 2002, Edmonton, Alberta, Canada.
  2. ↑ Н. Паклин. «Кластеризация категорийных данных: масштабируемый алгоритм CLOPE». Электронное издание. http://www.basegroup.ru/clusterization/clope.htm
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Антонина_Егорова/Алгоритм_кластеризации_категориальных_данных_CLOPE&oldid=22165