Алгоритм продольно-поперечной прогонки: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Ateina (обсуждение | вклад) |
Ateina (обсуждение | вклад) |
||
| (не показано 9 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | {{algorithm | ||
| + | | name = Алгоритм продольно-поперечной прогонки<br /> | ||
| + | | input_data = <math>(N_{x} + 1)(N_{y} + 1)</math> | ||
| + | | output_data = <math>(N_{x} + 1)(N_{y} + 1)</math> | ||
| + | }} | ||
| + | |||
| + | Основные авторы описания: [[Участник:Ateina|Дружкина А.И.]], [[Участник:Likhoded|Лиходед Н.А.]] | ||
| + | |||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
===Общее описание алгоритма=== | ===Общее описание алгоритма=== | ||
Продольно–поперечная схема, которая также носит название метода переменных направлений (ADI – alternate directions implicit method), получила широкое применение для решения многомерных задач, приводящих к уравнениям в частных производных параболического типа (уравнение диффузии, уравнение теплопроводности). Эта схема была предложена в 1955 году Писменом и Рэкфордом. | Продольно–поперечная схема, которая также носит название метода переменных направлений (ADI – alternate directions implicit method), получила широкое применение для решения многомерных задач, приводящих к уравнениям в частных производных параболического типа (уравнение диффузии, уравнение теплопроводности). Эта схема была предложена в 1955 году Писменом и Рэкфордом. | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| + | Рассмотрим в области | ||
| + | |||
| + | <math>\begin{align} D_{T}=G\times [0\leq t\leq T], \\ | ||
| + | G=[0\leq x\leq l_{x}]\times[0\leq y\leq l_{y}]\end{align}</math> | ||
| + | |||
| + | двумерное нелинейное уравнение теплопроводности | ||
| + | |||
| + | <math>\frac{\partial u}{\partial t} = \frac{\partial }{\partial x_{1}}\left ( k_{1}(x_{1}, x_{2}, t)\frac{\partial }{\partial x_{1}} \right ) + \frac{\partial }{\partial x_{2}}\left ( k_{1}(x_{1}, x_{2}, t)\frac{\partial }{\partial x_{2}} \right ) + f\left ( x_{1}, x_{2}, t \right ) | ||
| + | </math> | ||
| + | |||
| + | с начальными | ||
| + | |||
| + | <math>T(x,y,0) = T_{0}(x,y), (x,y)\in G,</math> | ||
| + | |||
| + | и граничными условиями | ||
| + | |||
| + | <math>T(x,y,t)|_{S_{T}} = \mu (x,y,t), (x,y,t)\in S_{T}\equiv \partial D_{T}</math> | ||
| + | |||
| + | Введем в области <math>G</math> сетку узлов <math>\bar{\omega_{h}} = \left \{ x^{i}=i\cdot h_{x}, i=0,1,...,N_{x}, N_{x}\cdot h_{x}=l_{x},y^{j}=j\cdot h_{y}, j=0,1,...,N_{y}, N_{y}\cdot h_{y}=l_{y} \right \} | ||
| + | </math>, а на отрезке <math>[0\leq t\leq T]</math> сетку узлов <math>\omega_{\tau } = \left \{ t_{j}=n\tau, n=0,1,...,k, k\tau=T \right \}. | ||
| + | </math>. Запишем разностную схему для заданной задачи (<math>k_{1} = k_{2} = \lambda | ||
| + | </math>): | ||
| + | |||
| + | <math>\left\{\begin{matrix} | ||
| + | \frac{y_{i,j}^{n+\frac{1}{2}} - y_{i,j}^{n}}{\tau} = \frac{1}{2}\left ( \frac{\lambda_{i+\frac{1}{2}, j}(y_{i+1,j}^{n+\frac{1}{2}} - y_{i,j}^{n+\frac{1}{2}}) - \lambda_{i-\frac{1}{2}, j}(y_{i,j}^{n+\frac{1}{2}} - y_{i-1,j}^{n+\frac{1}{2}})}{h_{x}^{2}} \right ) | ||
| + | + | ||
| + | \frac{1}{2}\left ( \frac{\lambda_{i, j+\frac{1}{2}}(y_{i,j+1}^{n} - y_{i,j}^{n}) - \lambda_{i, j-\frac{1}{2}}(y_{i,j}^{n} - y_{i,j-1}^{n})}{h_{y}^{2}} \right ), | ||
| + | \\ \frac{y_{i,j}^{n+1} - y_{i,j}^{n+\frac{1}{2}}}{\tau} = \frac{1}{2}\left ( \frac{\lambda_{i+\frac{1}{2}, j}(y_{i+1,j}^{n+\frac{1}{2}} - y_{i,j}^{n+\frac{1}{2}}) - \lambda_{i-\frac{1}{2}, j}(y_{i,j}^{n+\frac{1}{2}} - y_{i-1,j}^{n+\frac{1}{2}})}{h_{x}^{2}} \right ) | ||
| + | + | ||
| + | \frac{1}{2}\left ( \frac{\lambda_{i, j+\frac{1}{2}}(y_{i,j+1}^{n+1} - y_{i,j}^{n+1}) - \lambda_{i, j-\frac{1}{2}}(y_{i,j}^{n+1} - y_{i,j-1}^{n+1})}{h_{y}^{2}} \right ) | ||
| + | \end{matrix}\right.</math> | ||
| + | |||
| + | где | ||
| + | <math>\lambda _{i\pm \frac{1}{2}, j} = \frac{\lambda _{i\pm 1, j} + \lambda _{i, j}}{2}, | ||
| + | </math> | ||
| + | <math>\lambda _{i, j\pm \frac{1}{2}} = \frac{\lambda _{i, j\pm 1} + \lambda _{i, j}}{2}. | ||
| + | </math> | ||
| + | |||
| + | Зафиксировав в первом из уравнений системы <math>j</math>, получим систему уравнений относительно значений <math>y_{i,j}^{n+\frac{1}{2}}</math>, где <math>j = 1,...,N_{x}-1</math>, состоящую из (<math>N_{x}-1</math>) линейного уравнения, которую можно решить методом прогонки. | ||
| + | В целом систему на каждом половинном временном слое можно представить как (<math>N_{x}-1</math>) независимую задачу (для каждого фиксированного <math>j</math>), решаемую методом прогонки. | ||
| + | Аналогично решение второго из уравнений системы на каждом слое <math>t_{n+1}</math> представляет собой решение (<math>N_{x}-1</math>) независимой задачи при фиксированном <math>i</math>. Каждая из указанных задач является системой линейных уравнений относительно значений сеточной функции по неявному направлению и решается методом прогонки. | ||
| + | Сеточная функция , является приближенным решением задачи. | ||
| + | По каждому из неявных направлений разностная схема является линейной и может быть записана в следующем виде: | ||
| + | |||
| + | <math>A_{i,j}y_{i-1,j}^{n+\frac{1}{2}} + C_{i,j}y_{i,j}^{n+\frac{1}{2}} + B_{i,j}y_{i+1,j}^{n+\frac{1}{2}} = F_{i,j}^{n}</math> | ||
| + | |||
| + | <math>A_{i,j} = \frac{\lambda_{i-\frac{1}{2},j}}{-2h_{y}^{2}}, | ||
| + | |||
| + | B_{i,j} = \frac{\lambda_{i+\frac{1}{2},j}}{-2h_{y}^{2}}, | ||
| + | |||
| + | C_{i,j} = \frac{1}{\tau} - A_{i,j} - B_{i,j},</math> | ||
| + | |||
| + | <math>F_{i,j}^{n+\frac{1}{2}} = \frac{y_{i,j}^{n+\frac{1}{2}}}{\tau} + \frac{\lambda _{i+\frac{1}{2}, j}(y_{i+1, j}^{n+\frac{1}{2}} - y_{i, j}^{n+\frac{1}{2}}) - \lambda _{i-\frac{1}{2}, j}(y_{i,j}^{n+\frac{1}{2}} - y_{i-1, j}^{n+\frac{1}{2}})}{h_{y}^{2}}</math> | ||
| + | |||
| + | и соответственно | ||
| + | |||
| + | <math>A_{i,j}y_{i,j-1}^{n+1} + C_{i,j}y_{i,j}^{n+1} + B_{i,j}y_{i,j+1}^{n+1} = F_{i,j}^{n+\frac{1}{2}}. | ||
| + | </math> | ||
| + | |||
| + | Для решения уравнений воспользуемся формулами прогонки. Значения прогоночных коэффициентов находятся по рекуррентным формулам: | ||
| + | |||
| + | где <math>k</math> – индекс неявного направления. | ||
| + | Из граничных условий при <math>k=0</math> и <math>k=N</math> определяются значения прогоночных коэффициентов. При этом <math>\alpha _{0}</math> и <math>\alpha _{N}</math> равны нулю, а значения <math>\beta _{0}</math> и <math>\beta _{N}</math> определяются из соответствующих краевых условий. | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| Строка 12: | Строка 83: | ||
===Схема реализации последовательного алгоритма=== | ===Схема реализации последовательного алгоритма=== | ||
Последовательность исполнения метода следующая: | Последовательность исполнения метода следующая: | ||
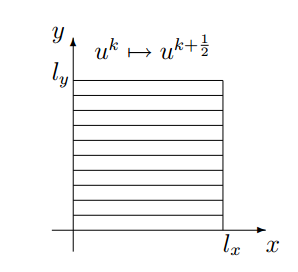
| − | Осуществляется прогонка вдоль строк, как это изображено на рисунке | + | Осуществляется прогонка вдоль строк, как это изображено на рисунке: |
| − | + | ||
| − | + | [[Файл:Adi method 1.png|300px|thumb|center|Прогонка вдоль строк]] | |
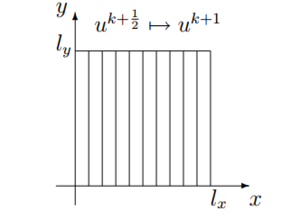
| − | Затем осуществляется прогонка вдоль столбцов, как это представлено на рисунке | + | Затем осуществляется прогонка вдоль столбцов, как это представлено на рисунке: |
| − | + | [[Файл:Adi_method_2.png|300px|thumb|center|Прогонка вдоль столбцов]] | |
===Последовательная сложность алгоритма=== | ===Последовательная сложность алгоритма=== | ||
| Строка 43: | Строка 114: | ||
Продольно–поперечная схема равномерно и безусловно устойчива по начальным данным, так как при переходе с одного целого слоя на следующий целый слой ошибки начальных данных не нарастают. | Продольно–поперечная схема равномерно и безусловно устойчива по начальным данным, так как при переходе с одного целого слоя на следующий целый слой ошибки начальных данных не нарастают. | ||
При переходе с целого слоя на целый погрешность локальной аппроксимации на равномерных сетках есть <math>O(\tau^{2} + h_{x}^{2} + h_{y}^{2})</math> т.е. продольно–поперечная схема имеет второй порядок аппроксимации по всем переменным. | При переходе с целого слоя на целый погрешность локальной аппроксимации на равномерных сетках есть <math>O(\tau^{2} + h_{x}^{2} + h_{y}^{2})</math> т.е. продольно–поперечная схема имеет второй порядок аппроксимации по всем переменным. | ||
| + | |||
| + | == Программная реализация алгоритма== | ||
| + | ===Особенности реализации последовательного алгоритма=== | ||
| + | Вычислительные процессы реализаций, основанных на естественном параллелизме, могут на каждом временном слое выполняться независимо. | ||
| + | |||
| + | ===Локальность данных и вычислений=== | ||
| + | |||
| + | ===Возможные способы и особенности параллельной реализации алгоритма=== | ||
| + | Вычислительные процессы реализаций, основанных на естественном параллелизме, на каждом временном слое могут выполняться независимо, но при переходе к новому слою требуют групповых коммуникаций “каждый с каждым”. С ростом числа используемых процессов это приводит к большим накладным расходам. | ||
| + | Локальность алгоритма – это вычислительное свойство, отражающее степень использования при реализации алгоритма памяти с быстрым доступом. При многопроцессорной обработке памятью с быстрым доступом считается локальная память процессора. В этой работе вместо части естественного параллелизма предлагается использовать конвейерный параллелизм. Такой параллелизм приводит к разгону и торможению вычислительного конвейера на каждом временном слое, но позволяет построить параллельный алгоритм с улучшенной локальностью (с существенно меньшим объемом коммуникационных операций). | ||
| + | |||
| + | ====Вычислительный алгоритм продольно-поперечной прогонки==== | ||
| + | Основную вычислительную часть алгоритма, реализующего двухшаговую разностную схему продольно–поперечной прогонки, т.е. метода переменных направлений, можно представить в виде следующего псевдокода (циклы, итерации которых заведомо можно выполнять независимо, запишем как dopar): | ||
| + | <source> | ||
| + | do j =1, j0 | ||
| + | dopar i2= 1, N2 –1 | ||
| + | do i1= 1, N1 –1 | ||
| + | S1: | ||
| + | S2: | ||
| + | enddo | ||
| + | do i1= 1, N1 –1 | ||
| + | S3: | ||
| + | enddo | ||
| + | enddopar | ||
| + | dopar i1= 1, N1 –1 | ||
| + | do i2= 1, N2 –1 | ||
| + | S4: | ||
| + | S5: | ||
| + | enddo | ||
| + | do i2= 1, N2 –1 | ||
| + | S6: | ||
| + | enddo | ||
| + | enddopar | ||
| + | enddo(j) | ||
| + | </source> | ||
| + | Здесь (i) и (i) – коэффициенты прогонки, возникающие при решении промежуточных систем линейных алгебраических уравнений. Конечные значения являются приближенным решением задачи. | ||
| + | Алгоритм метода переменных направлений обладает естественным параллелизмом: можно организовать независимые вычислительные процессы на каждом временном слое. Так как число вычислительных ядер обычно гораздо меньше N1 и N2, то при реализации на параллельных компьютерах с распределенной памятью итерации циклов, отмеченных как dopar, следует сгруппировать и получить макрооперации, называемые зернами вычислений или тайлами. Процесс получения макроопераций–тайлов называется тайлингом. | ||
| + | |||
| + | ====Параллельный алгоритм с улучшенной локальностью==== | ||
| + | Коммуникационные операции алгоритма порождаются информационными зависимостями между вычислительными операциями. Зависимости Sα(I)→Sβ(J) между операциями (I, J – итерации алгоритма) будем характеризовать векторами зависимостей dα,β=J–I. Вектор dα,β позволяет для операции Sβ(J) найти операцию Sα(I), от которой Sβ(J) зависит. Зависимости представленного алгоритма переменных направлений определяются векторами d1,1=d1,2=d2,2=d3,3=(0,0,1), d1,3=d2,3=(0,0,2i1–N1), d6,2=(1,i1–i2+φ,i1+i2–N2), где φ равно 0, 1, –1, d4,4=d4,5=d5,5=d6,6=(0,0,1), d4,6=d5,6=(0,0,2i2–N2), d3,5=(0, i2–i1+φ,i1+i2–N1), где φ равно 0, 1, –1. | ||
| + | При получении параллельного алгоритма, основанном на естественном параллелизме, распределение всех операций алгоритма между процессами определяется параллельными циклами уровня вложенности 2. Коммуникационные операции порождаются только векторами d6,2 и d3,5; у остальных векторов вторая координата нулевая, поэтому они не порождают обменов данными. На каждом новом временном слое вычисления требуют групповых коммуникационных операций: происходят обращения каждого процесса к локальной памяти всех других процессов. | ||
| + | Рассмотрим альтернативный вариант: распределение между процессами операций, порождаемых операторами S4, S5, S6, по–прежнему определяется параллельными циклами уровня вложенности 2, а распределение операций, порождаемых операторами S1, S2, S3, определяется параллельными циклами уровня вложенности 3. Можно показать, что коммуникационные операции порождаются векторами d1,1, d1,2, d2,2, d3,3, d6,2, но суммарный объем коммуникационных операций значительно уменьшается и обмен происходит только между процессами, номера которых отличаются на 1. | ||
| + | Таким образом, в альтернативном (новом) параллельном алгоритме для операций, порождаемых операторами S1, S2, S3, требуется организовать вычислительные конвейеры, но операции и данные перераспределены между процессами таким образом, что значительная часть данных приватизирована процессами и не требует коммуникационных операций. | ||
| + | Пусть P – число процессов, предназначенных для реализации алгоритма, числа Q2 и r2 связаны соотношением r2= . Будем предполагать, что r1=(N1–1)/P является целым числом. Структуру кода выполнения алгоритма для каждого процесса p, 0 p P–1, можно представить в следующем виде: | ||
| + | |||
| + | <syntaxhighlight line start="1"> | ||
| + | do j =1, j0 | ||
| + | do q2= 0, Q2 –1 | ||
| + | dopar i2= 1 + q2 r2, min((q2 +1)r2, N2 –1) // Начало тайла 0-го типа | ||
| + | do i1= 1 + p r1, (p +1)r1 | ||
| + | S1: | ||
| + | S2: | ||
| + | enddo | ||
| + | enddopar // Конец тайла 0-го типа. Обмен данными | ||
| + | enddo(q2) | ||
| + | do q2= 0, Q2 –1 | ||
| + | dopar i2= 1 + q2 r2, min((q2 +1)r2, N2 –1) // Начало тайла 1-го типа | ||
| + | do i1= 1 + (P–p–1) r1, (P–p)r1 | ||
| + | S3: | ||
| + | enddo | ||
| + | enddopar // Конец тайла 1-го типа. Обмен «граничными» данными | ||
| + | enddo(q2) | ||
| + | dopar i1= 1 + p r1, (p +1)r1 // Начало тайла 2-го типа | ||
| + | do i2= 1, N2 –1 | ||
| + | S4: | ||
| + | S5: | ||
| + | enddo | ||
| + | do i2= 1, N2 –1 | ||
| + | S6: | ||
| + | enddo | ||
| + | enddopar(i1) // Конец тайла 2-го типа. Обмен данными не требуется | ||
| + | enddo(j) | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | ====Параллельный алгоритм, основанный на судоку-распределении операций между процессами==== | ||
| + | Приведем еще параллельный алгоритм, основанный на так называемом судоку-распределении операций между процессами. Использование судоку-распределения позволяет уменьшить объём коммуникационных операций, избежать групповых коммуникаций “каждый с каждым”. | ||
| + | Структуру кода выполнения алгоритма для каждого процессора p, 0≤p≤P, можно представить в следующем виде: | ||
| + | |||
| + | <syntaxhighlight> | ||
| + | do n = 0, k | ||
| + | do igl = 0, P – 1 | ||
| + | do jgl = 0, P – 1 | ||
| + | if (p == (P – igl + jgl) mod P) | ||
| + | dopar j = 1 + jgl r2, min(( jgl + 1)r2, Ny - 1) // Начало тайла 1-го типа | ||
| + | do i = 1 + igl r1, min((igl + 1)r1, Nx - 1) | ||
| + | |||
| + | |||
| + | enddo(i) | ||
| + | enddopar(j) // Конец тайла 1-го типа, обмен граничными данными | ||
| + | endif | ||
| + | enddo(jgl) | ||
| + | enddo(igl) | ||
| + | do igl = P – 1, 0 | ||
| + | do jgl = 0, P – 1 | ||
| + | if (p == (P – igl + jgl)) mod P) | ||
| + | dopar j = 1 + jgl r2, min(( jgl + 1)r2, Ny - 1) // Начало тайла 2-го типа | ||
| + | do i = min((igl + 1)r1, Nx - 1), 1 + igl r1 | ||
| + | |||
| + | enddo(i) | ||
| + | enddopar(j) // Конец тайла 2-го типа, обмен граничными данными | ||
| + | endif | ||
| + | enddo(jgl) | ||
| + | enddo(igl) | ||
| + | do jgl = 0, P – 1 | ||
| + | do igl = 0, P – 1 | ||
| + | if (p == (P – igl + jgl) mod P) | ||
| + | dopar i = 1 + igl r1, min((igl + 1)r1, Nx – 1) // Начало тайла 3-го типа | ||
| + | do j = 1 + jgl r2, min(( jgl + 1)r2, Ny - 1) | ||
| + | |||
| + | |||
| + | enddo(j) | ||
| + | enddopar(i) // Конец тайла 3-го типа, обмен граничными данными | ||
| + | endif | ||
| + | enddo(igl) | ||
| + | enddo(jgl) | ||
| + | do jgl = P – 1, 0 | ||
| + | do igl = 0, P – 1 | ||
| + | if (p == (P – igl + jgl) mod P) | ||
| + | dopar i = 1 + igl r1, min(( igl + 1)r1, Nx - 1) // Начало тайла 4-го типа | ||
| + | do j = min((jgl + 1)r2, Ny - 1), 1 + jgl r2 | ||
| + | |||
| + | enddo(j) | ||
| + | enddopar(i) // Конец тайла 4-го типа, обмен граничными данными | ||
| + | endif | ||
| + | enddo(igl) | ||
| + | enddo(jgl) | ||
| + | enddo(n) | ||
| + | </syntaxhighlight> | ||
| + | ===Масштабируемость алгоритма и его реализации=== | ||
| + | |||
| + | ===Динамические характеристики и эффективность реализации алгоритма=== | ||
| + | |||
| + | ===Выводы для классов архитектур=== | ||
| + | |||
| + | ===Существующие реализации алгоритма=== | ||
| + | В языке Matlab существует реализация алгоритма продольно-поперечной прогонки. | ||
| + | Также метод продольно–поперечной прогонки реализован в библиотеке для решения дифференциальных уравнений языка Python. | ||
Текущая версия на 01:19, 13 июня 2017
| Алгоритм продольно-поперечной прогонки | |
| Последовательный алгоритм | |
| Объём входных данных | [math](N_{x} + 1)(N_{y} + 1)[/math] |
| Объём выходных данных | [math](N_{x} + 1)(N_{y} + 1)[/math] |
Основные авторы описания: Дружкина А.И., Лиходед Н.А.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Продольно–поперечная схема, которая также носит название метода переменных направлений (ADI – alternate directions implicit method), получила широкое применение для решения многомерных задач, приводящих к уравнениям в частных производных параболического типа (уравнение диффузии, уравнение теплопроводности). Эта схема была предложена в 1955 году Писменом и Рэкфордом.
1.2 Математическое описание алгоритма
Рассмотрим в области
[math]\begin{align} D_{T}=G\times [0\leq t\leq T], \\ G=[0\leq x\leq l_{x}]\times[0\leq y\leq l_{y}]\end{align}[/math]
двумерное нелинейное уравнение теплопроводности
[math]\frac{\partial u}{\partial t} = \frac{\partial }{\partial x_{1}}\left ( k_{1}(x_{1}, x_{2}, t)\frac{\partial }{\partial x_{1}} \right ) + \frac{\partial }{\partial x_{2}}\left ( k_{1}(x_{1}, x_{2}, t)\frac{\partial }{\partial x_{2}} \right ) + f\left ( x_{1}, x_{2}, t \right ) [/math]
с начальными
[math]T(x,y,0) = T_{0}(x,y), (x,y)\in G,[/math]
и граничными условиями
[math]T(x,y,t)|_{S_{T}} = \mu (x,y,t), (x,y,t)\in S_{T}\equiv \partial D_{T}[/math]
Введем в области [math]G[/math] сетку узлов [math]\bar{\omega_{h}} = \left \{ x^{i}=i\cdot h_{x}, i=0,1,...,N_{x}, N_{x}\cdot h_{x}=l_{x},y^{j}=j\cdot h_{y}, j=0,1,...,N_{y}, N_{y}\cdot h_{y}=l_{y} \right \} [/math], а на отрезке [math][0\leq t\leq T][/math] сетку узлов [math]\omega_{\tau } = \left \{ t_{j}=n\tau, n=0,1,...,k, k\tau=T \right \}. [/math]. Запишем разностную схему для заданной задачи ([math]k_{1} = k_{2} = \lambda [/math]):
[math]\left\{\begin{matrix} \frac{y_{i,j}^{n+\frac{1}{2}} - y_{i,j}^{n}}{\tau} = \frac{1}{2}\left ( \frac{\lambda_{i+\frac{1}{2}, j}(y_{i+1,j}^{n+\frac{1}{2}} - y_{i,j}^{n+\frac{1}{2}}) - \lambda_{i-\frac{1}{2}, j}(y_{i,j}^{n+\frac{1}{2}} - y_{i-1,j}^{n+\frac{1}{2}})}{h_{x}^{2}} \right ) + \frac{1}{2}\left ( \frac{\lambda_{i, j+\frac{1}{2}}(y_{i,j+1}^{n} - y_{i,j}^{n}) - \lambda_{i, j-\frac{1}{2}}(y_{i,j}^{n} - y_{i,j-1}^{n})}{h_{y}^{2}} \right ), \\ \frac{y_{i,j}^{n+1} - y_{i,j}^{n+\frac{1}{2}}}{\tau} = \frac{1}{2}\left ( \frac{\lambda_{i+\frac{1}{2}, j}(y_{i+1,j}^{n+\frac{1}{2}} - y_{i,j}^{n+\frac{1}{2}}) - \lambda_{i-\frac{1}{2}, j}(y_{i,j}^{n+\frac{1}{2}} - y_{i-1,j}^{n+\frac{1}{2}})}{h_{x}^{2}} \right ) + \frac{1}{2}\left ( \frac{\lambda_{i, j+\frac{1}{2}}(y_{i,j+1}^{n+1} - y_{i,j}^{n+1}) - \lambda_{i, j-\frac{1}{2}}(y_{i,j}^{n+1} - y_{i,j-1}^{n+1})}{h_{y}^{2}} \right ) \end{matrix}\right.[/math]
где [math]\lambda _{i\pm \frac{1}{2}, j} = \frac{\lambda _{i\pm 1, j} + \lambda _{i, j}}{2}, [/math] [math]\lambda _{i, j\pm \frac{1}{2}} = \frac{\lambda _{i, j\pm 1} + \lambda _{i, j}}{2}. [/math]
Зафиксировав в первом из уравнений системы [math]j[/math], получим систему уравнений относительно значений [math]y_{i,j}^{n+\frac{1}{2}}[/math], где [math]j = 1,...,N_{x}-1[/math], состоящую из ([math]N_{x}-1[/math]) линейного уравнения, которую можно решить методом прогонки. В целом систему на каждом половинном временном слое можно представить как ([math]N_{x}-1[/math]) независимую задачу (для каждого фиксированного [math]j[/math]), решаемую методом прогонки. Аналогично решение второго из уравнений системы на каждом слое [math]t_{n+1}[/math] представляет собой решение ([math]N_{x}-1[/math]) независимой задачи при фиксированном [math]i[/math]. Каждая из указанных задач является системой линейных уравнений относительно значений сеточной функции по неявному направлению и решается методом прогонки. Сеточная функция , является приближенным решением задачи. По каждому из неявных направлений разностная схема является линейной и может быть записана в следующем виде:
[math]A_{i,j}y_{i-1,j}^{n+\frac{1}{2}} + C_{i,j}y_{i,j}^{n+\frac{1}{2}} + B_{i,j}y_{i+1,j}^{n+\frac{1}{2}} = F_{i,j}^{n}[/math]
[math]A_{i,j} = \frac{\lambda_{i-\frac{1}{2},j}}{-2h_{y}^{2}}, B_{i,j} = \frac{\lambda_{i+\frac{1}{2},j}}{-2h_{y}^{2}}, C_{i,j} = \frac{1}{\tau} - A_{i,j} - B_{i,j},[/math]
[math]F_{i,j}^{n+\frac{1}{2}} = \frac{y_{i,j}^{n+\frac{1}{2}}}{\tau} + \frac{\lambda _{i+\frac{1}{2}, j}(y_{i+1, j}^{n+\frac{1}{2}} - y_{i, j}^{n+\frac{1}{2}}) - \lambda _{i-\frac{1}{2}, j}(y_{i,j}^{n+\frac{1}{2}} - y_{i-1, j}^{n+\frac{1}{2}})}{h_{y}^{2}}[/math]
и соответственно
[math]A_{i,j}y_{i,j-1}^{n+1} + C_{i,j}y_{i,j}^{n+1} + B_{i,j}y_{i,j+1}^{n+1} = F_{i,j}^{n+\frac{1}{2}}. [/math]
Для решения уравнений воспользуемся формулами прогонки. Значения прогоночных коэффициентов находятся по рекуррентным формулам:
где [math]k[/math] – индекс неявного направления. Из граничных условий при [math]k=0[/math] и [math]k=N[/math] определяются значения прогоночных коэффициентов. При этом [math]\alpha _{0}[/math] и [math]\alpha _{N}[/math] равны нулю, а значения [math]\beta _{0}[/math] и [math]\beta _{N}[/math] определяются из соответствующих краевых условий.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма можно считать состоящим из двух частей – продольной прогонки и поперечной прогонки. В свою очередь, каждая из этих прогонок состоит из прямого и обратного хода. В прямом ходе вычислительное ядро составляют последовательности операций деления, умножения и сложения/вычитания. В обратном ходе в вычислительном ядре остаются только последовательности умножения и сложения.
1.4 Макроструктура алгоритма
Алгоритм представляет собой совокупность продольной и поперечной прогонки, а также прямого и обратного хода.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая: Осуществляется прогонка вдоль строк, как это изображено на рисунке:
Затем осуществляется прогонка вдоль столбцов, как это представлено на рисунке:
1.6 Последовательная сложность алгоритма
Таким образом, при классификации по последовательной сложности продольно–поперечная прогонка относится к алгоритмам с линейной сложностью. При переходе от слоя [math]j[/math] к слою [math]j+1[/math] требуется [math]O(\frac{1}{h^{2}})[/math] арифметических действий. Чтобы найти [math]y^{j_{0}}[/math] при [math]t_{0} = j_{0}\tau[/math] по начальным данным требуется, очевидно, [math]O(\frac{1}{h^{2}})j_{0} = O(\frac{1}{\tau h^{2}})[/math] операций, то есть число операций пропорционально числу используемых узлов пространственно–временной сетки [math]w_{h\tau}[/math]. Наряду с основными значениями [math]u_{ij}^{k}[/math] и [math]u_{i,j}^{k+1}[/math] вводится значение на промежуточном слое – [math]u_{ij}^{k+\frac{1}{2}}[/math], что фактически является значением [math]u[/math] при [math]t = t_{k+\frac{1}{2}}=t+\frac{\tau}{2}[/math]. Благодаря этому, переход на следующий слой осуществляется в два шага.
1.7 Информационный граф
1.8 Описание ресурса параллелизма алгоритма
Алгоритм метода переменных направлений обладает естественным параллелизмом: можно организовать независимые вычислительные процессы на каждом временном слое.
1.9 Входные и выходные данные алгоритма
Входные данные: матрица [math]y[/math] (элементы [math]y_{i,j}^{1}, i = 0,...,N_{x}, j = 0,...,N_{y}[/math]).
Конечные значения [math]y_{(2)}(i_{1}, i_{2})[/math] являются приближенным решением задачи
Выходные данные: обновленная матрица [math]y[/math] (элементы [math]y_{i,j}^{n+1}, i = 0,...,N_{x}, j = 0,...,N_{y}[/math]).
Объём выходных данных: [math](N_{x} + 1) * (N_{y} + 1)[/math]
1.10 Свойства алгоритма
Продольно–поперечная схема является одной из первых экономичных схем. Она сочетает в себе лучшее качество явной схемы – экономичность и неявной – устойчивость. Основной идеей экономичных разностных схем является сведение многомерной задачи к цепочке одномерных задач. Продольно–поперечная схема равномерно и безусловно устойчива по начальным данным, так как при переходе с одного целого слоя на следующий целый слой ошибки начальных данных не нарастают. При переходе с целого слоя на целый погрешность локальной аппроксимации на равномерных сетках есть [math]O(\tau^{2} + h_{x}^{2} + h_{y}^{2})[/math] т.е. продольно–поперечная схема имеет второй порядок аппроксимации по всем переменным.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Вычислительные процессы реализаций, основанных на естественном параллелизме, могут на каждом временном слое выполняться независимо.
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
Вычислительные процессы реализаций, основанных на естественном параллелизме, на каждом временном слое могут выполняться независимо, но при переходе к новому слою требуют групповых коммуникаций “каждый с каждым”. С ростом числа используемых процессов это приводит к большим накладным расходам. Локальность алгоритма – это вычислительное свойство, отражающее степень использования при реализации алгоритма памяти с быстрым доступом. При многопроцессорной обработке памятью с быстрым доступом считается локальная память процессора. В этой работе вместо части естественного параллелизма предлагается использовать конвейерный параллелизм. Такой параллелизм приводит к разгону и торможению вычислительного конвейера на каждом временном слое, но позволяет построить параллельный алгоритм с улучшенной локальностью (с существенно меньшим объемом коммуникационных операций).
2.3.1 Вычислительный алгоритм продольно-поперечной прогонки
Основную вычислительную часть алгоритма, реализующего двухшаговую разностную схему продольно–поперечной прогонки, т.е. метода переменных направлений, можно представить в виде следующего псевдокода (циклы, итерации которых заведомо можно выполнять независимо, запишем как dopar):
do j =1, j0
dopar i2= 1, N2 –1
do i1= 1, N1 –1
S1:
S2:
enddo
do i1= 1, N1 –1
S3:
enddo
enddopar
dopar i1= 1, N1 –1
do i2= 1, N2 –1
S4:
S5:
enddo
do i2= 1, N2 –1
S6:
enddo
enddopar
enddo(j)Здесь (i) и (i) – коэффициенты прогонки, возникающие при решении промежуточных систем линейных алгебраических уравнений. Конечные значения являются приближенным решением задачи. Алгоритм метода переменных направлений обладает естественным параллелизмом: можно организовать независимые вычислительные процессы на каждом временном слое. Так как число вычислительных ядер обычно гораздо меньше N1 и N2, то при реализации на параллельных компьютерах с распределенной памятью итерации циклов, отмеченных как dopar, следует сгруппировать и получить макрооперации, называемые зернами вычислений или тайлами. Процесс получения макроопераций–тайлов называется тайлингом.
2.3.2 Параллельный алгоритм с улучшенной локальностью
Коммуникационные операции алгоритма порождаются информационными зависимостями между вычислительными операциями. Зависимости Sα(I)→Sβ(J) между операциями (I, J – итерации алгоритма) будем характеризовать векторами зависимостей dα,β=J–I. Вектор dα,β позволяет для операции Sβ(J) найти операцию Sα(I), от которой Sβ(J) зависит. Зависимости представленного алгоритма переменных направлений определяются векторами d1,1=d1,2=d2,2=d3,3=(0,0,1), d1,3=d2,3=(0,0,2i1–N1), d6,2=(1,i1–i2+φ,i1+i2–N2), где φ равно 0, 1, –1, d4,4=d4,5=d5,5=d6,6=(0,0,1), d4,6=d5,6=(0,0,2i2–N2), d3,5=(0, i2–i1+φ,i1+i2–N1), где φ равно 0, 1, –1. При получении параллельного алгоритма, основанном на естественном параллелизме, распределение всех операций алгоритма между процессами определяется параллельными циклами уровня вложенности 2. Коммуникационные операции порождаются только векторами d6,2 и d3,5; у остальных векторов вторая координата нулевая, поэтому они не порождают обменов данными. На каждом новом временном слое вычисления требуют групповых коммуникационных операций: происходят обращения каждого процесса к локальной памяти всех других процессов. Рассмотрим альтернативный вариант: распределение между процессами операций, порождаемых операторами S4, S5, S6, по–прежнему определяется параллельными циклами уровня вложенности 2, а распределение операций, порождаемых операторами S1, S2, S3, определяется параллельными циклами уровня вложенности 3. Можно показать, что коммуникационные операции порождаются векторами d1,1, d1,2, d2,2, d3,3, d6,2, но суммарный объем коммуникационных операций значительно уменьшается и обмен происходит только между процессами, номера которых отличаются на 1. Таким образом, в альтернативном (новом) параллельном алгоритме для операций, порождаемых операторами S1, S2, S3, требуется организовать вычислительные конвейеры, но операции и данные перераспределены между процессами таким образом, что значительная часть данных приватизирована процессами и не требует коммуникационных операций. Пусть P – число процессов, предназначенных для реализации алгоритма, числа Q2 и r2 связаны соотношением r2= . Будем предполагать, что r1=(N1–1)/P является целым числом. Структуру кода выполнения алгоритма для каждого процесса p, 0 p P–1, можно представить в следующем виде:
do j =1, j0
do q2= 0, Q2 –1
dopar i2= 1 + q2 r2, min((q2 +1)r2, N2 –1) // Начало тайла 0-го типа
do i1= 1 + p r1, (p +1)r1
S1:
S2:
enddo
enddopar // Конец тайла 0-го типа. Обмен данными
enddo(q2)
do q2= 0, Q2 –1
dopar i2= 1 + q2 r2, min((q2 +1)r2, N2 –1) // Начало тайла 1-го типа
do i1= 1 + (P–p–1) r1, (P–p)r1
S3:
enddo
enddopar // Конец тайла 1-го типа. Обмен «граничными» данными
enddo(q2)
dopar i1= 1 + p r1, (p +1)r1 // Начало тайла 2-го типа
do i2= 1, N2 –1
S4:
S5:
enddo
do i2= 1, N2 –1
S6:
enddo
enddopar(i1) // Конец тайла 2-го типа. Обмен данными не требуется
enddo(j)2.3.3 Параллельный алгоритм, основанный на судоку-распределении операций между процессами
Приведем еще параллельный алгоритм, основанный на так называемом судоку-распределении операций между процессами. Использование судоку-распределения позволяет уменьшить объём коммуникационных операций, избежать групповых коммуникаций “каждый с каждым”. Структуру кода выполнения алгоритма для каждого процессора p, 0≤p≤P, можно представить в следующем виде:
do n = 0, k
do igl = 0, P – 1
do jgl = 0, P – 1
if (p == (P – igl + jgl) mod P)
dopar j = 1 + jgl r2, min(( jgl + 1)r2, Ny - 1) // Начало тайла 1-го типа
do i = 1 + igl r1, min((igl + 1)r1, Nx - 1)
enddo(i)
enddopar(j) // Конец тайла 1-го типа, обмен граничными данными
endif
enddo(jgl)
enddo(igl)
do igl = P – 1, 0
do jgl = 0, P – 1
if (p == (P – igl + jgl)) mod P)
dopar j = 1 + jgl r2, min(( jgl + 1)r2, Ny - 1) // Начало тайла 2-го типа
do i = min((igl + 1)r1, Nx - 1), 1 + igl r1
enddo(i)
enddopar(j) // Конец тайла 2-го типа, обмен граничными данными
endif
enddo(jgl)
enddo(igl)
do jgl = 0, P – 1
do igl = 0, P – 1
if (p == (P – igl + jgl) mod P)
dopar i = 1 + igl r1, min((igl + 1)r1, Nx – 1) // Начало тайла 3-го типа
do j = 1 + jgl r2, min(( jgl + 1)r2, Ny - 1)
enddo(j)
enddopar(i) // Конец тайла 3-го типа, обмен граничными данными
endif
enddo(igl)
enddo(jgl)
do jgl = P – 1, 0
do igl = 0, P – 1
if (p == (P – igl + jgl) mod P)
dopar i = 1 + igl r1, min(( igl + 1)r1, Nx - 1) // Начало тайла 4-го типа
do j = min((jgl + 1)r2, Ny - 1), 1 + jgl r2
enddo(j)
enddopar(i) // Конец тайла 4-го типа, обмен граничными данными
endif
enddo(igl)
enddo(jgl)
enddo(n)2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В языке Matlab существует реализация алгоритма продольно-поперечной прогонки. Также метод продольно–поперечной прогонки реализован в библиотеке для решения дифференциальных уравнений языка Python.