Алгоритм Форда-Фалкерсона: различия между версиями
| [непроверенная версия] | [досмотренная версия] |
ASA (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показаны 3 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{level-a}} | ||
| + | |||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| Строка 48: | Строка 50: | ||
=== Информационный граф === | === Информационный граф === | ||
| + | |||
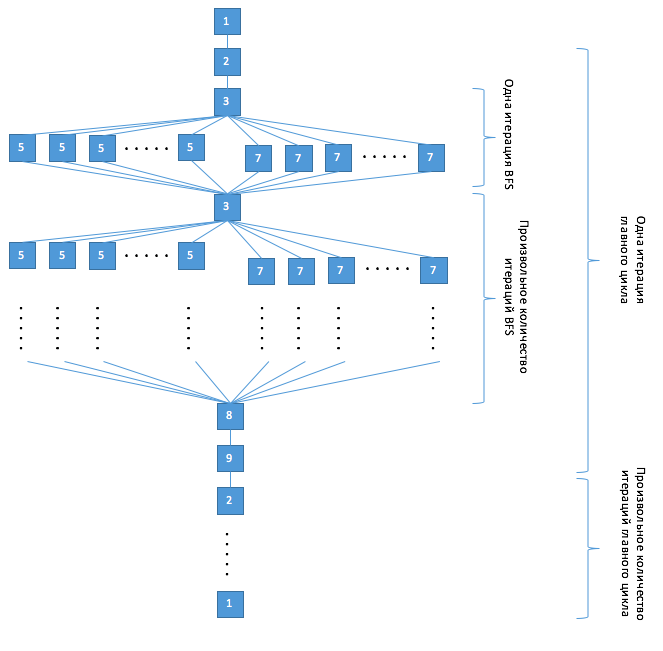
| + | Далее представлен информационный граф алгоритма, демонстрирующий описанные уровни параллелизма. Информационный граф алгоритма — ориентированный граф, состоящий из вершин, соответствующих операциям алгоритма, и направленных дуг, соответствующих передаче данных (результаты одних операций передаются в качестве аргументов другим операциям) между ними. | ||
| + | |||
| + | [[file:Max flow.png|thumb|center|1000px|Рисунок 1 – Информационный граф алгоритма Форда-Фалкерсона]] | ||
| + | |||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
Основной объём вычислений в алгоритме Форда-Фалкерсона приходится на поиск путей от источника к стоку. С этой целью может применяться [[Поиск в ширину (BFS)|поиск в ширину]], который хорошо распараллеливается. Наилучших результатов можно достичь, если распределить вершины между узлами по слоям примерно одинаковой толщины, так что в каждом слое вершины были бы примерно на одинаковом удалении от источника (такое расслоение также можно найти поиском в ширину). | Основной объём вычислений в алгоритме Форда-Фалкерсона приходится на поиск путей от источника к стоку. С этой целью может применяться [[Поиск в ширину (BFS)|поиск в ширину]], который хорошо распараллеливается. Наилучших результатов можно достичь, если распределить вершины между узлами по слоям примерно одинаковой толщины, так что в каждом слое вершины были бы примерно на одинаковом удалении от источника (такое расслоение также можно найти поиском в ширину). | ||
| Строка 56: | Строка 63: | ||
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | |||
| − | |||
| − | |||
| − | |||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| − | === | + | === Результаты прогонов === |
| − | |||
| − | |||
| − | |||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Литература == | == Литература == | ||
| Строка 77: | Строка 72: | ||
[[Категория:Начатые статьи]] | [[Категория:Начатые статьи]] | ||
| + | |||
| + | [[en:Ford–Fulkerson algorithm]] | ||
Текущая версия на 09:31, 7 июля 2022
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм Форда-Фалкерсона[1][2] (с последующими усовершенствованиями Эдмондса-Карпа[3] и Е. А. Диница[4]) предназначен для решения задачи о максимальном потоке в транспортной сети. Время работы алгоритма [math]O(n^2m)[/math] (для алгоритма Диница). В случае целых пропускных способностей, не превосходящих [math]K[/math], сложность [math]O(Km)[/math] (для алгоритма Эдмондса–Карпа).
Алгоритм последовательно улучшает допустимый поток, находя так называемый дополняющий путь и увеличивая поток вдоль этого пути. Варианты алгоритма отличаются способом нахождения дополняющего пути.
- В исходном алгоритме Форда–Фалкерсона способ выбора дополняющего пути не уточнялся.
- В алгоритме Эдмондса-Карпа выбирается кратчайший дополняющий путь, для чего используется поиск в ширину на каждой итерации;
- В алгоритме Диница для выбора кратчайшего пути поддерживается «расслоение» графа, так что поиск в ширину выполняется значительно реже.
1.2 Математическое описание алгоритма
Математическая постановка задачи приведена в статье «Поиск максимального потока в транспортной сети», там же введены используемые обозначения.
Пусть задан некоторый допустимый поток [math]f[/math]. Дополняющим путём называется последовательность рёбер [math]e_0 = (s, v_1), e_1 = (v_1, v_2), \ldots, e_k = (v_k, t)[/math], каждое из которых обладает положительной остаточной пропускной способностью [math]c_f(e_i) = c(e_i) - f(e_i) \gt 0[/math].
Поток останется допустимым, если увеличить его вдоль дополняющего пути на число [math]\delta = \min \{ c(e_i) - f(e_i) \} \gt 0[/math], при этом величина потока возрастёт на то же число [math]\delta[/math]. Для сохранения антисимметричности увеличение потока производится присваиваниями
- [math] f(e_i) \leftarrow f(e_i) + \delta, \quad f(e_i^R) \leftarrow f(e_i^R) - \delta, \quad i = \overline{0, k}. [/math]
Если дополняющего пути не существует, то поток [math]f[/math] является максимальным.
1.3 Вычислительное ядро алгоритма
Вычислительными ядрами, на которые приходится наибольший объём вычислений, являются:
- поиск в ширину;
- увеличение потока вдоль дополняющего пути.
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
1.6 Последовательная сложность алгоритма
В статье Эдмондса–Карпа[3] (теорема 1) доказано, что количество последовательно построенных кратчайших дополнительных путей не превосходит [math]m(n + 1)/2 = O(mn)[/math]. Основными операциями алгоритма являются поиск в ширину сложностью [math]O(m)[/math] и обновление потока вдоль дополняющего пути сложностью [math]O(n)[/math].
В алгоритме Эдмондса–Карпа выполняются следующие операции:
- поиск в ширину и определение кратчайшего пути на каждой итерации, сложность [math]O(m + n)[/math], общая сложность [math]O(m^2n)[/math];
- обновление потока вдоль дополняющего пути, сложность [math]O(n)[/math], общая сложность [math]O(n^2 m)[/math].
Таким образом, общая сложность составляет [math]O(m^2n)[/math].
В алгоритме Диница выполняются следующие операции:
- поиск кратчайшего пути и обновление потока вдоль дополняющего пути на каждой итерации, сложность [math]O(n)[/math], общая сложность [math]O(mn^2)[/math];
- обновление расслоения на каждой итерации, сложность [math]O(1)[/math], общая сложность [math]O(mn)[/math];
- поиск в ширину для построения нового расслоения, сложность [math]O(m)[/math], число построений не более [math]n[/math], общая сложность [math]O(mn)[/math].
Таким образом, общая сложность составляет [math]O(mn^2)[/math].
1.7 Информационный граф
Далее представлен информационный граф алгоритма, демонстрирующий описанные уровни параллелизма. Информационный граф алгоритма — ориентированный граф, состоящий из вершин, соответствующих операциям алгоритма, и направленных дуг, соответствующих передаче данных (результаты одних операций передаются в качестве аргументов другим операциям) между ними.
1.8 Ресурс параллелизма алгоритма
Основной объём вычислений в алгоритме Форда-Фалкерсона приходится на поиск путей от источника к стоку. С этой целью может применяться поиск в ширину, который хорошо распараллеливается. Наилучших результатов можно достичь, если распределить вершины между узлами по слоям примерно одинаковой толщины, так что в каждом слое вершины были бы примерно на одинаковом удалении от источника (такое расслоение также можно найти поиском в ширину).
1.9 Входные и выходные данные алгоритма
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Возможные способы и особенности параллельной реализации алгоритма
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
3 Литература
- ↑ Ford, L R, Jr., and D R Fulkerson. “Maximal Flow Through a Network.” Canadian Journal of Mathematics 8 (1956): 399–404. doi:10.4153/CJM-1956-045-5.
- ↑ Ford, L R, Jr., and D R Fulkerson. “A Simple Algorithm for Finding Maximal Network Flows and an Application to the Hitchcock Problem.” Canadian Journal of Mathematics 9 (1957): 210–18.
- ↑ 3,0 3,1 Edmonds, Jack, and Richard M Karp. “Theoretical Improvements in Algorithmic Efficiency for Network Flow Problems.” Journal of the ACM 19, no. 2 (April 1972): 248–64. doi:10.1145/321694.321699.
- ↑ Диниц, Е. А. “Алгоритм решения задачи о максимальном потоке в сети со степенной оценкой.” Доклады АН СССР 194, no. 4 (1970): 754–57.