|
|
| (не показано 79 промежуточных версий этого же участника) |
| Строка 1: |
Строка 1: |
| − | {{algorithm
| |
| − | | name = QR-факторизация
| |
| − | | serial_complexity = <math>O(n^3)</math>
| |
| − | | pf_height = <math>O(n)</math>
| |
| − | | pf_width = <math>O(n^2)</math>
| |
| − | | input_data = <math>n^2</math>
| |
| − | | output_data = <math>2\cdot n^2</math>
| |
| − | }}
| |
| − |
| |
| | Автор: [[Участник:Grinch96|Г. А. Балыбердин]] | | Автор: [[Участник:Grinch96|Г. А. Балыбердин]] |
| | | | |
| Строка 16: |
Строка 7: |
| | Пусть <math>A = (a_1, ..., a_n)</math> - вещественная матрица <math>n × n</math>, определитель которой не равен <math>0</math>. Во многих приложениях требуется решать линейную систему <math>Ax=b</math> c плохо-обусловленной матрицей <math>A</math>. При решении данной задачи, чтобы не увеличивать число обусловленности матрицы <math>A</math>, ее можно представить в виде <math>A=QR</math>, где матрица <math>Q \in \mathbb{R}^{n×n}</math> состоит из ортонормированных строк, а матрица <math> R \in \mathbb{R}^{n×n}</math> является верхнетреугольной. В итоге мы получаем так называемую <math>QR</math>-факторизацию. | | Пусть <math>A = (a_1, ..., a_n)</math> - вещественная матрица <math>n × n</math>, определитель которой не равен <math>0</math>. Во многих приложениях требуется решать линейную систему <math>Ax=b</math> c плохо-обусловленной матрицей <math>A</math>. При решении данной задачи, чтобы не увеличивать число обусловленности матрицы <math>A</math>, ее можно представить в виде <math>A=QR</math>, где матрица <math>Q \in \mathbb{R}^{n×n}</math> состоит из ортонормированных строк, а матрица <math> R \in \mathbb{R}^{n×n}</math> является верхнетреугольной. В итоге мы получаем так называемую <math>QR</math>-факторизацию. |
| | | | |
| − | Чтобы построить <math>QR</math>-факторизацию можно воспользоваться процессом [https://algowiki-project.org/ru/Участник:KibAndrey/Ортогонализация_Грама-Шмидта ортогонализации Грама-Шмидта], однако в условиях машинной арифметики, матрица <math>Q</math> может получиться далекой от ортогональной.Чтобы этого избежать, на определенных итерациях нужно проводить процесс реортогонализации. | + | Чтобы построить <math>QR</math>-факторизацию можно воспользоваться процессом [https://algowiki-project.org/ru/Участник:KibAndrey/Ортогонализация_Грама-Шмидта ортогонализации Грама-Шмидта]<ref> Тыртышников Е.Е. Методы численного анализа // М.: 2006. 83 с.</ref>, однако в условиях машинной арифметики, матрица <math>Q</math> может получиться далекой от ортогональной.Чтобы этого избежать, на определенных итерациях нужно проводить процесс реортогонализации <ref>Luc Giraud, Julien Langou, Miroslav Rozložník, Jasper van den Eshof. Rounding error analysis of the classical Gram-Schmidt orthogonalization process // Springer-Verlag, 2005.</ref>. |
| | | | |
| | === Математическое описание алгоритма === | | === Математическое описание алгоритма === |
| Строка 29: |
Строка 20: |
| | \begin{align} | | \begin{align} |
| | & p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\ | | & p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\ |
| − | & q_{j} = p_{j} / ||p_{j}||_{2}, \quad j = 1, \ldots , n\\ | + | & q_{j} = p_{j} / ||p_{j}||_{2}, \\ |
| − | & r_{ij} = q_{i}^{T} a_{j}. | + | & r_{ij} = q_{i}^{T} a_{j},\quad i = 1, \ldots , j - 1.\\ |
| | \end{align} | | \end{align} |
| | </math> | | </math> |
| Строка 36: |
Строка 27: |
| | Здесь <math>q_{i}, \, a_{i} </math> столбцы матриц <math> Q, \, A </math> соответственно. | | Здесь <math>q_{i}, \, a_{i} </math> столбцы матриц <math> Q, \, A </math> соответственно. |
| | | | |
| − | На <math>m</math>-ом шаге получаем <math>\tilde{Q}_{m} \in \mathbb{R}^{n × m}</math>. Если <math>||\tilde{Q}_{m}^{T} \tilde{Q}_{m} - I|| > k</math>, запускается процесс реортогонализации. <math>k</math> произвольная и задает точность ортогональности матрицы <math>Q</math>. В [A ROBUST ..... REORTHOGONALIZATION] <math>k</math> рекомендуется брать равным корню из машинной точности. | + | На <math>m</math>-ом шаге получаем <math>p_{m} \in \mathbb{R}^{n}</math>. Если <math>||a_{m}||_{2}/||p_{m}||_{2} > k</math>, запускается процесс реортогонализации. <math>k</math> произвольная и задает точность ортогональности матрицы <math>Q</math>. В посвященной методу реортогонализации статье <ref>Luc Giraud and Jilien Langou. A robust criterion for the modified Gram–Schmidt algorithm with selective reorthogonalization // Society for Industrial and Applied Mathematic, 2003.</ref> <math>k</math> рекомендуется брать равным <math>10</math>, однако приводятся примеры алгоритмов, где <math>k=\sqrt{2}</math> или <math>k=\sqrt{5}</math>. Мы исследуем <math>k=10</math>. |
| | | | |
| − | Суть процесса реортогонализации - это процесс ортогонализации Грама-Шмидта, примененный к матрице <math>\tilde{Q}_{m}</math> на <math>m</math>-оm шаге алгоритма. Более формально: | + | Суть процесса реортогонализации - это процесс ортогонализации Грама-Шмидта, примененный повторно к вектору <math>p_{m}</math> на <math>m</math>-оm шаге алгоритма. Более формально: |
| | | | |
| | <math> | | <math> |
| | \begin{align} | | \begin{align} |
| − | & \tilde{p}_{j} = \tilde{q}_{j} - \sum_{i=1}^{j-1} \tilde{q}_{i} (\tilde{q}_{i}^{T} \tilde{q}_{j}), \\ | + | & \tilde{p}_{m} = p_{m} - \sum_{i=1}^{m-1} q_{i} (q_{i}^{T} p_{m}), \\ |
| − | & q_{j} = \tilde{p}_{j} / ||\tilde{p}_{j}||_{2}, \quad j = 1, \ldots , m \\ | + | & q_{m} = \tilde{p}_{m} / ||\tilde{p}_{m}||_{2}, \\ |
| − | & \tilde{r}_{ij} = \tilde{q}_{i}^{T} \tilde{q}_{j}. \\ | + | & \tilde{r}_{mj} = q_{j}^{T} p_{m}, \quad j = 1, \ldots , m - 1, \\ |
| − | & r_{ij} = \tilde{r}_{ij} + r_{ij}^{0} | + | & r_{mj} = \tilde{r}_{mj} + r_{mj}^{0}, \quad j = 1, \ldots , m - 1, \\ |
| | + | & r_{mm} = ||\tilde{p}_{m}||_{2}. |
| | \end{align} | | \end{align} |
| | </math> | | </math> |
| | | | |
| − | Здесь <math>\tilde{q}_{i}</math> столбцы матриц <math> \tilde{Q}_{m}</math>, <math>r_{ij}^{0}</math> - элемент матриц <math>R</math>, вычисленный до реортогонализации. | + | Здесь <math>\tilde{q}_{i}</math> столбцы матриц <math> \tilde{Q}_{m}</math>, <math>r_{mj}^{0}</math> - элементы матрицы <math>R</math>, вычисленные до реортогонализации. |
| | | | |
| | === Вычислительное ядро алгоритма === | | === Вычислительное ядро алгоритма === |
| | | | |
| − | Вычислительное ядро алгоритма состоит из вычисления: | + | Вычислительное ядро алгоритма, если не требуется реортогонализация, состоит из вычисления: |
| | | | |
| − | *<math>\dfrac{k(k+1)}{2}</math> скалярных произведений векторов, включая вычисление длины вектора; | + | *<math>\dfrac{n(n+1)}{2}</math> скалярных произведений векторов, включая вычисление длины вектора; |
| | | | |
| − | *<math>\dfrac{(k-1)k}{2}</math> умножений векторов на число. | + | *<math>\dfrac{(n-1)n}{2}</math> умножений векторов на число. |
| | + | |
| | + | На каждом шаге реортогонализации добавляется <math> j-1 </math> вычислений скалярных произведений векторов на число и столько же умножений вектора на число. Здесь реортогонализация производится на <math>j</math>-ом шаге. Однако сколько раз алгоритм будет реортогонализовывать вектора зависит от свойств матрицы. |
| | | | |
| | === Макроструктура алгоритма === | | === Макроструктура алгоритма === |
| | | | |
| − | Как записано и в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть метода составляют множественные (всего <math>\frac{n (n - 1)}{2}</math>) вычисления сумм | + | Как записано и в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть процесса составляют скалярные произведения векторов и умножения вектора на число: |
| | | | |
| − | :<math>a_{ji}-\sum_{p=1}^{i-1}l_{ip} l_{jp}</math>
| + | <math> |
| | + | \begin{align} |
| | + | & p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\ |
| | + | & q_{j} = p_{j} / ||p_{j}||_{2}. |
| | + | \end{align} |
| | + | </math> |
| | | | |
| − | в режиме накопления или без него.
| + | как если алгоритм реортогонализует повторно вектора, так и без реортогонализаций. |
| | | | |
| | === Схема реализации последовательного алгоритма === | | === Схема реализации последовательного алгоритма === |
| | | | |
| − | Последовательность исполнения метода следующая: | + | Последовательность исполнения процесса следующая: |
| − | | |
| − | 1. <math>l_{11}= \sqrt{a_{11}}</math>
| |
| | | | |
| − | 2. <math>l_{j1}= \frac{a_{j1}}{l_{11}}</math> (при <math>j</math> от <math>2</math> до <math>n</math>).
| + | 1. <math> q_1 = \frac{a_1}{||a_1||_2} </math> |
| | | | |
| − | Далее для всех <math>i</math> от <math>2</math> до <math>n</math> по нарастанию выполняются | + | Далее для всех <math> i = 2, n </math>: |
| | | | |
| − | 3. <math>l_{ii} = \sqrt{a_{ii} - \sum_{p = 1}^{i - 1} l_{ip}^2}</math> и
| + | 2. <math> r_{ij} = q_{j}^{T} a_{i},\quad j = 1, \ldots , i - 1 </math> |
| | | | |
| − | 4. (кроме <math>i = n</math>): <nowiki/><math>l_{ji} = \left (a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp} \right ) / l_{ii}</math> (для всех <math>j</math> от <math>i + 1</math> до <math>n</math>).
| + | 3. <math> p_{i} = a_{i} - \sum_{j=1}^{i-1} q_{j} r_{ij}</math> |
| | | | |
| − | После этого (если <math>i < n</math>) происходит переход к шагу 3 с бо́льшим <math>i</math>.
| + | Если <math>||a_{i}||_{2}/||p_{i}||_{2} > k</math>, выполнить 4, 5, 6. Иначе перейти сразу к 7: |
| | | | |
| − | Особо отметим, что вычисления сумм вида <math>a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math> в обеих формулах производят в режиме накопления вычитанием из <math>a_{ji}</math> произведений <math>l_{ip} l_{jp}</math> для <math>p</math> от <math>1</math> до <math>i - 1</math>, c нарастанием <math>p</math>.
| + | 4. <math> r_{ij}^{0} = q_{j}^{T} p_{i},\quad j = 1, \ldots , i - 1 </math> |
| | | | |
| − | === Последовательная сложность алгоритма === | + | 5. <math> p_{i} = p_{i} - \sum_{j=1}^{i-1} q_{j} r_{ij}^{0}, \quad j = 1, \ldots , i - 1 </math> |
| | | | |
| − | Для разложения матрицы порядка n методом Холецкого в последовательном (наиболее быстром) варианте требуется:
| + | 6. <math> r_{ij} = r_{ij}^{0} + r_{ij},\quad j = 1, \ldots , i - 1 </math> |
| − |
| |
| − | * <math>n</math> вычислений квадратного корня,
| |
| − | * <math>\frac{n(n-1)}{2}</math> делений,
| |
| − | * <math>\frac{n^3-n}{6}</math> сложений (вычитаний),
| |
| − | * <math>\frac{n^3-n}{6}</math> умножений.
| |
| | | | |
| − | Умножения и сложения (вычитания) составляют ''основную часть алгоритма''.
| + | 7. <math> r_{ii} = ||p_{i}||_{2} </math> |
| − |
| |
| − | При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает долю умножений и сложений/вычитаний во времени, требуемом для выполнения метода Холецкого.
| |
| | | | |
| − | При классификации по последовательной сложности, таким образом, метод Холецкого относится к алгоритмам ''с кубической сложностью''.
| + | 8. <math> q_{i} = p_{i} / r_{ii} </math> |
| | | | |
| − | === Информационный граф ===
| + | Здесь (как и везде) под второй нормой подразумевается: |
| | | | |
| − | Опишем [[глоссарий#Граф алгоритма|граф алгоритма]]<ref>Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.</ref><ref>Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.</ref><ref>Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.</ref> как аналитически, так и в виде рисунка.
| + | <math> ||x||_2 = \sqrt{x_1^2 + x_2^{2} + \ldots + x_n^2} </math> |
| | | | |
| − | Граф алгоритма состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности.
| + | === Последовательная сложность алгоритма === |
| | | | |
| − | '''Первая''' группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию SQRT.
| + | Для факторизации матрицы порядка n процессом Грама-Шмидта в последовательном варианте без реортогонализации требуется: |
| − | Единственная координата каждой из вершин <math>i</math> меняется в диапазоне от <math>1</math> до <math>n</math>, принимая все целочисленные значения.
| |
| | | | |
| − | Аргумент этой функции
| + | * <math>n</math> извлечений квадратного корня, |
| − |
| + | * <math>n</math> делений, |
| − | * при <math>i = 1</math> — элемент ''входных данных'', а именно <math>a_{11}</math>; | + | * <math>(n-1)(n^2+2n-1)</math> сложений (вычитаний), |
| − | * при <math>i > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i - 1</math>, <math>i</math>, <math>i - 1</math>. | + | * <math>n(n^2+2n-2)</math> умножений. |
| − | Результат срабатывания операции является ''выходным данным'' <math>l_{ii}</math>.
| |
| | | | |
| − | '''Вторая''' группа вершин расположена в двумерной области, соответствующая ей операция <math>a / b</math>.
| + | Если реортогонализация работает на каждом шаге (чего никогда не случается, однако предположим худший случай), то количество всех операций удвоится. Таким образом, умножения и сложения (вычитания) составляют основную часть алгоритма. |
| − | Естественно введённые координаты области таковы:
| |
| − | * <math>i</math> — меняется в диапазоне от <math>1</math> до <math>n-1</math>, принимая все целочисленные значения;
| |
| − | * <math>j</math> — меняется в диапазоне от <math>i+1</math> до <math>n</math>, принимая все целочисленные значения.
| |
| | | | |
| − | Аргументы операции следующие:
| + | При классификации по последовательной сложности, процесс ортогонализации Грама-Шмидта с реортогонализацией относится к алгоритмам с кубической сложностью. |
| − | *<math>a</math>:
| |
| − | ** при <math>i = 1</math> — элементы ''входных данных'', а именно <math>a_{j1}</math>;
| |
| − | ** при <math>i > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i - 1, j, i - 1</math>;
| |
| − | * <math>b</math> — результат срабатывания операции, соответствующей вершине из первой группы, с координатой <math>i</math>.
| |
| | | | |
| − | Результат срабатывания операции является ''выходным данным'' <math>l_{ji}</math>.
| + | === Информационный граф === |
| | | | |
| − | '''Третья''' группа вершин расположена в трёхмерной области, соответствующая ей операция <math>a - b * c</math>.
| + | Опишем вершины информационного графа. |
| − | Естественно введённые координаты области таковы:
| |
| − | * <math>i</math> — меняется в диапазоне от <math>2</math> до <math>n</math>, принимая все целочисленные значения;
| |
| − | * <math>j</math> — меняется в диапазоне от <math>i</math> до <math>n</math>, принимая все целочисленные значения;
| |
| − | * <math>p</math> — меняется в диапазоне от <math>1</math> до <math>i - 1</math>, принимая все целочисленные значения.
| |
| | | | |
| − | Аргументы операции следующие:
| + | 1. <math> a_i, \; i = 1 \ldots n </math> — столбцы исходной матрицы <math> A </math>; подаются на вход программе. |
| − | *<math>a</math>:
| |
| − | ** при <math>p = 1</math> элемент входных данных <math>a_{ji}</math>;
| |
| − | ** при <math>p > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i, j, p - 1</math>;
| |
| − | *<math>b</math> — результат срабатывания операции, соответствующей вершине из второй группы, с координатами <math>p, i</math>;
| |
| − | *<math>c</math> — результат срабатывания операции, соответствующей вершине из второй группы, с координатами <math>p, j</math>;
| |
| | | | |
| − | Результат срабатывания операции является ''промежуточным данным'' алгоритма.
| + | 2. <math> N </math> — операция взятия нормы вектора. |
| | | | |
| − | Описанный граф можно посмотреть на рис.1 и рис.2, выполненных для случая <math>n = 4</math>. Здесь вершины первой группы обозначены жёлтым цветом и буквосочетанием sq, вершины второй — зелёным цветом и знаком деления, третьей — красным цветом и буквой f. Вершины, соответствующие операциям, производящим выходные данные алгоритма, выполнены более крупно. Дублирующие друг друга дуги даны как одна. На рис.1 показан граф алгоритма согласно классическому определению , на рис.2 к графу алгоритма добавлены вершины , соответствующие входным (обозначены синим цветом) и выходным (обозначены розовым цветом) данным.
| + | 3. <math> div </math> — операция деления вектора на число. |
| | | | |
| − | [[file:Cholesky full.png|thumb|center|1400px|Рисунок 1. Граф алгоритма без отображения входных и выходных данных. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление.]]
| + | 4. <math> Sc </math> — операция взятия скалярного произведения двух векторов. |
| − | [[file:Cholesky full_in_out.png|thumb|center|1400px|Рисунок 2. Граф алгоритма с отображением входных и выходных данных. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление, In - входные данные, Out - результаты.]]
| |
| | | | |
| − | <center> | + | 5. <math> F </math> — операция вычитания из вектора произведение числа на вектор. |
| − | {{#widget:Algoviewer
| |
| − | |url=cholesky/Algo_view_cholesky4.html
| |
| − | |width=1300
| |
| − | |height=800
| |
| − | |border=1
| |
| − | }}
| |
| − | <br/> | |
| − | Интерактивное изображение графа алгоритма без входных и выходных данных для n = 4.
| |
| − | </center>
| |
| | | | |
| − | === Ресурс параллелизма алгоритма ===
| + | 6. <math> + </math> — операция суммирования двух чисел. |
| | | | |
| − | Для разложения матрицы порядка <math>n</math> методом Холецкого в параллельном варианте требуется последовательно выполнить следующие ярусы:
| + | 7. <math> r_{ij} </math>, <math> q_i, \; i = 1 \ldots n, \; j = 1 \ldots n </math> — элементы матрицы <math> R </math> и столбцы матрицы <math> Q </math> соответственно; выходные данные программы. |
| − | * <math>n</math> ярусов с вычислением квадратного корня (единичные вычисления в каждом из ярусов),
| |
| − | * <math>n - 1</math> ярус делений (в каждом из ярусов линейное количество делений, в зависимости от яруса — от <math>1</math> до <math>n - 1</math>),
| |
| − | * по <math>n - 1</math> ярусов умножений и сложений/вычитаний (в каждом из ярусов — квадратичное количество операций, от <math>1</math> до <math>\frac{n^2 - n}{2}</math>.
| |
| − |
| |
| − | Таким образом, в параллельном варианте, в отличие от последовательного, вычисления квадратных корней и делений будут определять довольно значительную долю требуемого времени. При реализации на конкретных архитектурах наличие в отдельных ярусах [[глоссарий#Ярусно-параллельная форма графа алгоритма|ЯПФ]] отдельных вычислений квадратных корней может породить и другие проблемы. Например, при реализации на ПЛИСах остальные вычисления (деления и тем более умножения и сложения/вычитания) могут быть конвейеризованы, что даёт экономию и по ресурсам на программируемых платах; вычисления же квадратных корней из-за их изолированности приведут к занятию ресурсов на платах, которые будут простаивать большую часть времени. Таким образом, общая экономия в 2 раза, из-за которой метод Холецкого предпочитают в случае симметричных задач тому же методу Гаусса, в параллельном случае уже имеет место вовсе не по всем ресурсам, и главное - не по требуемому времени.
| |
| | | | |
| − | При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения метода Холецкого в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает увеличение требуемой памяти почти в 2 раза.
| + | Информационный граф построен для матрицы размерности <math> 3 </math> при выполнении реортогонализации для третьего вектора. |
| | | | |
| − | При классификации по высоте ЯПФ, таким образом, метод Холецкого относится к алгоритмам со сложностью <math>O(n)</math>. При классификации по ширине ЯПФ его сложность будет <math>O(n^2)</math>.
| + | [[File:Grinch-graph.PNG]] |
| | | | |
| − | === Входные и выходные данные алгоритма ===
| + | Если объединить вершины N и div, Sc и F (вершины будут означать суперпозиции соответствующих операций), то получится следующий, чуть более простой для понимания, граф: |
| | | | |
| − | '''Входные данные''': плотная матрица <math>A</math> (элементы <math>a_{ij}</math>).
| + | [[File:Grinch graph 2.png]] |
| − | Дополнительные ограничения:
| |
| − | * <math>A</math> – симметрическая матрица, т. е. <math>a_{ij}= a_{ji}, i, j = 1, \ldots, n</math>.
| |
| − | * <math>A</math> – положительно определённая матрица, т. е. для любых ненулевых векторов <math>\vec{x}</math> выполняется <math>\vec{x}^T A \vec{x} > 0</math>.
| |
| | | | |
| − | '''Объём входных данных''': <math>\frac{n (n + 1)}{2}</math> (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. Например, в библиотеке, реализованной в НИВЦ МГУ, матрица A хранилась в одномерном массиве длины <math>\frac{n (n + 1)}{2}</math> по строкам своего нижнего треугольника.
| + | === Ресурс параллелизма алгоритма === |
| | | | |
| − | '''Выходные данные''': нижняя треугольная матрица <math>L</math> (элементы <math>l_{ij}</math>).
| + | В последовательной версии алгоритма двумя самыми трудоемкими операциями являются подсчет скалярных произведений и вычисление вектора, ортогонального предыдущим. Мы хотим добиться, чтобы каждый процессор считал "кусок" этих операций, однако также для ускорения работы программы нужно минимизировать число пересылок между процессорами. Пусть <math> k </math> - количество процессоров. Предлагается разбить исходную матрицу <math> A </math> на <math> k </math> блоков по <math> \frac{n}{k} </math> столбцов в каждом (<math> n </math> - размерность задачи), тогда каждый процессор будет решать задачу на "своем подпространстве". Таким образом мы добьемся количества пересылок порядка <math> O(kn) </math>, и параллельная сложность алгоритма составит <math> O( \frac{n^3}{k} ) </math>. |
| | | | |
| − | '''Объём выходных данных''': <math>\frac{n (n + 1)}{2}</math> (в силу треугольности достаточно хранить только ненулевые элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. Например, в той же библиотеке, созданной в НИВЦ МГУ, матрица <math>L</math> хранилась в одномерном массиве длины <math>\frac{n (n + 1)}{2}</math> по строкам своей нижней части.
| + | === Входные и выходные данные алгоритма === |
| | | | |
| − | === Свойства алгоритма ===
| + | '''Входные данные''': невырожденная матрица <math>A</math> (элементы <math>a_{ij}</math>). |
| | | | |
| − | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является ''квадратичным'' (отношение кубической к линейной).
| + | '''Объём входных данных''': <math>n^2</math>. |
| | | | |
| − | При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь ''линейна''.
| + | '''Выходные данные''': верхняя треугольная матрица <math>R</math> (элементы <math>r_{ij}</math>), унитарная матрица <math>Q</math> (элементы <math>q_{ij}</math>). |
| | | | |
| − | При этом алгоритм почти полностью детерминирован, это гарантируется теоремой о единственности разложения. Использование другого порядка выполнения ассоциативных операций может привести к накоплению ошибок округления, однако это влияние в используемых вариантах алгоритма не так велико, как, скажем, отказ от использования режима накопления.
| + | '''Объём выходных данных''': <math>\frac{n (n + 1)}{2} + n^2</math> (в силу треугольности матрицы <math>R</math> достаточно хранить только ее ненулевые элементы). |
| | | | |
| − | Дуги информационного графа, исходящие из вершин, соответствующих операциям квадратного корня и деления, образуют пучки т. н. рассылок линейной мощности (то есть степень исхода этих вершин и мощность работы с этими данными — линейная функция от порядка матрицы и координат этих вершин). При этом естественно наличие в этих пучках «длинных» дуг. Остальные дуги локальны.
| + | === Свойства алгоритма === |
| − | | |
| − | Наиболее известной является компактная укладка графа — его проекция на треугольник матрицы, который перевычисляется укладываемыми операциями. При этом «длинные» дуги можно убрать, заменив более дальнюю пересылку комбинацией нескольких ближних (к соседям).
| |
| − | | |
| − | [[Глоссарий#Эквивалентное возмущение|Эквивалентное возмущение]] <math>M</math> у метода Холецкого всего вдвое больше, чем возмущение <math>\delta A</math>, вносимое в матрицу при вводе чисел в компьютер:
| |
| − | <math>
| |
| − | ||M||_{E} \leq 2||\delta A||_{E}
| |
| − | </math>
| |
| − | | |
| − | Это явление обусловлено положительной определённостью матрицы. Среди всех используемых разложений матриц это наименьшее из эквивалентных возмущений.
| |
| | | | |
| | == Программная реализация алгоритма == | | == Программная реализация алгоритма == |
| | | | |
| | === Особенности реализации последовательного алгоритма === | | === Особенности реализации последовательного алгоритма === |
| − |
| |
| − | В простейшем (без перестановок суммирования) варианте метод Холецкого на Фортране можно записать так:
| |
| − | <source lang="fortran">
| |
| − | DO I = 1, N
| |
| − | S = A(I,I)
| |
| − | DO IP=1, I-1
| |
| − | S = S - DPROD(A(I,IP), A(I,IP))
| |
| − | END DO
| |
| − | A(I,I) = SQRT (S)
| |
| − | DO J = I+1, N
| |
| − | S = A(J,I)
| |
| − | DO IP=1, I-1
| |
| − | S = S - DPROD(A(I,IP), A(J,IP))
| |
| − | END DO
| |
| − | A(J,I) = S/A(I,I)
| |
| − | END DO
| |
| − | END DO
| |
| − | </source>
| |
| − | При этом для реализации режима накопления переменная <math>S</math> должна быть двойной точности.
| |
| − |
| |
| − | Отдельно следует обратить внимание на используемую в такой реализации функцию DPROD. Её появление как раз связано с тем, как математики могли использовать режим накопления вычислений. Дело в том, что, как правило, при выполнении умножения двух чисел с плавающей запятой сначала результат получается с удвоенными длинами мантиссы и порядка, и только при выполнении присваивания переменной одинарной точности результат округляется. Эта возможность даёт выполнять умножение действительных чисел с двойной точностью без предварительного приведения их к типу двойной точности. На ранних этапах развития вычислительных библиотек снятие результата без округление реализовали вставками специального кода в фортран-программы, но уже в 70-х гг. XX века в ряде трансляторов Фортрана появилась функция DPROD, реализующая это без обращения программиста к машинным кодам. Она была закреплена среди стандартных функций в стандарте Фортран 77, и реализована во всех современных трансляторах Фортрана.
| |
| − |
| |
| − | Для метода Холецкого существует блочная версия, которая отличается от точечной не тем, что операции над числами заменены на аналоги этих операций над блоками; её построение основано на том, что практически все циклы точечной версии имеют тип SchedDo в терминах методологии, основанной на исследовании информационного графа и, следовательно, могут быть развёрнуты. Тем не менее, обычно блочную версию метода Холецкого записывают не в виде программы с развёрнутыми и переставленными циклами, а в виде программы, подобной реализации точечного метода, в которой вместо соответствующих скалярных операций присутствуют операции над блоками.
| |
| − |
| |
| − | Особенностью размещения массивов в Фортране является хранение их "по столбцам" (быстрее всего меняется первый индекс). Поэтому для обеспечения локальности работы с памятью представляется более эффективной такая схема метода Холецкого (полностью эквивалентная описанной), когда исходная матрица и её разложение хранятся не в нижнем, а в верхнем треугольнике. Тогда при вычислениях скалярных произведений программа будет "идти" по последовательным ячейкам памяти компьютера.
| |
| − |
| |
| − | Есть и другой вариант точечной схемы: использовать вычисляемые элементы матрицы <math>L</math> в качестве аргументов непосредственно «сразу после» их вычисления. Такая программа будет выглядеть так:
| |
| − | <source lang="fortran">
| |
| − | DO I = 1, N
| |
| − | A(I,I) = SQRT (A(I, I))
| |
| − | DO J = I+1, N
| |
| − | A(J,I) = A(J,I)/A(I,I)
| |
| − | END DO
| |
| − | DO K=I+1,N
| |
| − | DO J = K, N
| |
| − | A(J,K) = A(J,K) - A(J,I)*A(K,I)
| |
| − | END DO
| |
| − | END DO
| |
| − | END DO
| |
| − | </source>
| |
| − | Как видно, в этом варианте для реализации режима накопления одинарной точности мы должны будем объявить двойную точность для массива, хранящего исходные данные и результат. Подчеркнём, что [[глоссарий#Граф алгоритма|граф алгоритма]] обеих схем - один и тот же (из п.1.7), если не считать изменением замену умножения на функцию DPROD!
| |
| | | | |
| | === Локальность данных и вычислений === | | === Локальность данных и вычислений === |
| − |
| |
| − | ==== Локальность реализации алгоритма ====
| |
| − |
| |
| − | ===== Структура обращений в память и качественная оценка локальности =====
| |
| − |
| |
| − | [[file:Cholesky_locality1.jpg|thumb|center|700px|Рисунок 3. Реализация метода Холецкого. Общий профиль обращений в память]]
| |
| − |
| |
| − | На рис.3 представлен профиль обращений в память<ref>Воеводин Вад. В. Визуализация и анализ профиля обращений в память // Вестник Южно-Уральского государственного университета. Серия Математическое моделирование и про-граммирование. — 2011. — Т. 17, № 234. — С. 76–84.</ref><ref>Воеводин Вл. В., Воеводин Вад. В. Спасительная локальность суперкомпьютеров // Открытые системы. — 2013. — № 9. — С. 12–15.</ref> для реализации метода Холецкого. В программе задействован только 1 массив, поэтому в данном случае обращения в профиле происходят только к элементам этого массива. Программа состоит из одного основного этапа, который, в свою очередь, состоит из последовательности подобных итераций. Пример одной итерации выделен зеленым цветом.
| |
| − |
| |
| − | Видно, что на каждой <math>i</math>-й итерации используются все адреса, начиная с некоторого, при этом адрес первого обрабатываемого элемента увеличивается. Также можно заметить, что число обращений в память на каждой итерации растет примерно до середины работы программы, после чего уменьшается вплоть до завершения работы. Это позволяет говорить о том, что данные в программе используются неравномерно, при этом многие итерации, особенно в начале выполнения программы, задействуют большой объем данных, что приводит к ухудшению локальности.
| |
| − |
| |
| − | Однако в данном случае основным фактором, влияющим на локальность работы с памятью, является строение итерации. Рассмотрим фрагмент профиля, соответствующий нескольким первым итерациям.
| |
| − |
| |
| − | [[file:Cholesky_locality2.jpg|thumb|center|700px|Рисунок 4. Реализация метода Холецкого. Фрагмент профиля (несколько первых итераций)]]
| |
| − |
| |
| − | Исходя из рис.4 видно, что каждая итерация состоит из двух различных фрагментов. Фрагмент 1 – последовательный перебор (с некоторым шагом) всех адресов, начиная с некоторого начального. При этом к каждому адресу происходит мало обращений. Такой фрагмент обладает достаточно неплохой пространственной локальностью, так как шаг по памяти между соседними обращениями невелик, но плохой временно́й локальностью, поскольку данные редко используются повторно.
| |
| − |
| |
| − | Фрагмент 2 устроен гораздо лучше с точки зрения локальности. В рамках этого фрагмента выполняется большое число обращений подряд к одним и тем же данным, что обеспечивает гораздо более высокую степень как пространственной, так и временно́й локальности по сравнению с фрагментом 1.
| |
| − |
| |
| − | После рассмотрения фрагмента профиля на рис.4 можно оценить общую локальность двух фрагментов на каждой итерации. Однако стоит рассмотреть более подробно, как устроен каждый из фрагментов.
| |
| − |
| |
| − | [[file:Cholesky_locality3.jpg|thumb|center|700px|Рисунок 5. Реализация метода Холецкого. Фрагмент профиля (часть одной итерации)]]
| |
| − |
| |
| − | Рис.5, на котором представлена часть одной итерации общего профиля (см. рис.3), позволяет отметить достаточно интересный факт: строение каждого из фрагментов на самом деле заметно сложнее, чем это выглядит на рис.4. В частности, каждый шаг фрагмента 1 состоит из нескольких обращений к соседним адресам, причем выполняется не последовательный перебор. Также можно увидеть, что фрагмент 2 на самом деле в свою очередь состоит из повторяющихся итераций, при этом видно, что каждый шаг фрагмента 1 соответствует одной итерации фрагмента 2 (выделено зеленым на рис.5). Это лишний раз говорит о том, что для точного понимания локальной структуры профиля необходимо его рассмотреть на уровне отдельных обращений.
| |
| − |
| |
| − | Стоит отметить, что выводы на основе рис.5 просто дополняют общее представлении о строении профиля обращений; сделанные на основе рис.4 выводы относительно общей локальности двух фрагментов остаются верны.
| |
| − |
| |
| − | ===== Количественная оценка локальности =====
| |
| − |
| |
| − | Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен [http://git.algowiki-project.org/Voevodin/locality/blob/master/benchmarks/holecky/holecky.h здесь] (функция Kernel). Условия запуска описаны [http://git.algowiki-project.org/Voevodin/locality/blob/master/README.md здесь].
| |
| − |
| |
| − | Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
| |
| − |
| |
| − | [[file:Cholesky_locality4.jpg|thumb|center|700px|Рисунок 6. Сравнение значений оценки daps]]
| |
| − |
| |
| − | На рис.6 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что реализация метода Холецкого характеризуется достаточно высокой скоростью взаимодействия с памятью, однако ниже, чем, например, у теста Линпак или реализации метода Якоби.
| |
| − |
| |
| − | Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
| |
| − |
| |
| − | [[file:Cholesky_locality5.jpg|thumb|center|700px|Рисунок 7. Сравнение значений оценки cvg]]
| |
| − |
| |
| − | На рис.7 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, реализация метода Холецкого оказалась ниже в списке по сравнению с оценкой daps.
| |
| | | | |
| | === Возможные способы и особенности параллельной реализации алгоритма === | | === Возможные способы и особенности параллельной реализации алгоритма === |
| − |
| |
| − | Как нетрудно видеть по структуре графа алгоритма, вариантов распараллеливания алгоритма довольно много. Например, во втором варианте (см. раздел «[[#Особенности реализации последовательного алгоритма|Особенности реализации последовательного алгоритма]]») все внутренние циклы параллельны, в первом — параллелен цикл по <math>J</math>. Тем не менее, простое распараллеливание таким способом «в лоб» вызовет такое количество пересылок между процессорами с каждым шагом по внешнему циклу, которое почти сопоставимо с количеством арифметических операций. Поэтому перед размещением операций и данных между процессорами вычислительной системы предпочтительно разбиение всего пространства вычислений на блоки, с сопутствующим разбиением обрабатываемого массива.
| |
| − |
| |
| − | Многое зависит от конкретного типа вычислительной системы. Присутствие конвейеров на узлах многопроцессорной системы делает рентабельным параллельное вычисление нескольких скалярных произведений сразу. Подобная возможность есть и на программировании ПЛИСов, но там быстродействие будет ограничено медленным последовательным выполнением операции извлечения квадратного корня.
| |
| − |
| |
| − | В принципе, возможно и использование т. н. «скошенного» параллелизма. Однако его на практике никто не использует, из-за усложнения управляющей структуры программы.
| |
| | | | |
| | === Масштабируемость алгоритма и его реализации === | | === Масштабируемость алгоритма и его реализации === |
| | | | |
| − | ==== Масштабируемость алгоритма ====
| + | Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. |
| | | | |
| − | ==== Масштабируемость реализации алгоритма ====
| + | Набор и границы значений изменяемых параметров запуска реализации алгоритма: |
| − | Проведём исследование масштабируемости параллельной реализации разложения Холецкого согласно [[Scalability methodology|методике]]. Исследование проводилось на суперкомпьютере "Ломоносов"<ref name="Lom">Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.</ref> [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета].
| |
| | | | |
| − | Набор и границы значений изменяемых [[Глоссарий#Параметры запуска|параметров запуска]] реализации алгоритма:
| + | число процессоров <math>2^k</math>, где k пробегает от 0 до 7; |
| | | | |
| − | * число процессоров [4 : 256] с шагом 4;
| + | размер матрицы <math>n^p</math>, где p пробегает от 8 до 12. |
| − | * размер матрицы [1024 : 5120].
| |
| | | | |
| − | В результате проведённых экспериментов был получен следующий диапазон [[Глоссарий#Эффективность реализации|эффективности реализации]] алгоритма:
| + | На следующем рисунке приведен график времени работы алгоритма (t) в зависимости от количества процессов (p) и размерности задачи (d): |
| | | | |
| − | * минимальная эффективность реализации 0,11%;
| + | [[File:Scale_1.jpg]] |
| − | * максимальная эффективность реализации 2,65%.
| |
| | | | |
| − | На следующих рисунках приведены графики [[Глоссарий#Производительность|производительности]] и эффективности выбранной реализации разложения Холецкого в зависимости от изменяемых параметров запуска.
| + | При увеличении количества процессов для задач разных (фиксированных) размерностей наблюдается общая закономерность: сначала время решения стремительно падает, потом не изменяется и далее начинает увеличиваться. Это связано с тем, что когда время работы программы падает, время пересылок много меньше времени работы процессов. При увеличении количества процессов увеличивается количество пересылок (и, следовательно, затраченное на них время) и в какой-то момент становится больше времени работы процессов. |
| − | | |
| − | [[file:Масштабируемость Параллельной реализации метода Холецкого Производительность3.png|thumb|center|700px|Рисунок 8. Параллельная реализация метода Холецкого. Изменение производительности в зависимости от числа процессоров и размера матрицы.]]
| |
| − | [[file:Холецкий масштабируемость эффективность2.png|thumb|center|700px|Рисунок 9. Параллельная реализация метода Холецкого. Изменение эффективности в зависимости от числа процессоров и размера матрицы.]]
| |
| − | | |
| − | Построим оценки масштабируемости выбранной реализации разложения Холецкого:
| |
| − | * По числу процессов: -0,000593. При увеличении числа процессов эффективность на рассмотренной области изменений параметров запуска уменьшается, однако в целом уменьшение не очень быстрое. Малая интенсивность изменения объясняется крайне низкой общей эффективностью работы приложения с максимумом в 2,65%, и значение эффективности на рассмотренной области значений быстро доходит до десятых долей процента. Это свидетельствует о том, что на большей части области значений нет интенсивного снижения эффективности. Это объясняется также тем, что с ростом [[Глоссарий#Вычислительная сложность|вычислительной сложности]] падение эффективности становится не таким быстрым. Уменьшение эффективности на рассмотренной области работы параллельной программы объясняется быстрым ростом накладных расходов на организацию параллельного выполнения. С ростом вычислительной сложности задачи эффективность снижается так же быстро, но при больших значениях числа процессов. Это подтверждает предположение о том, что накладные расходы начинают сильно превалировать над вычислениями.
| |
| − | * По размеру задачи: 0,06017. При увеличении размера задачи эффективность возрастает. Эффективность возрастает тем быстрее, чем большее число процессов используется для выполнения. Это подтверждает предположение о том, что размер задачи сильно влияет на эффективность выполнения приложения. Оценка показывает, что с ростом размера задачи эффективность на рассмотренной области значений параметров запуска сильно увеличивается. Также, учитывая разницу максимальной и минимальной эффективности в 2,5%, можно сделать вывод, что рост эффективности при увеличении размера задачи наблюдается на большей части рассмотренной области значений.
| |
| − | * По двум направлениям: 0,000403. При рассмотрении увеличения как вычислительной сложности, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности небольшая. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров небольшая, эффективность с увеличением масштабов возрастает, но медленно и с небольшими перепадами.
| |
| − | | |
| − | [http://git.algowiki-project.org/Teplov/Scalability/tree/master/cholesky-decomposition-master Исследованная параллельная реализация на языке C]
| |
| | | | |
| | === Динамические характеристики и эффективность реализации алгоритма === | | === Динамические характеристики и эффективность реализации алгоритма === |
| − |
| |
| − | Для проведения экспериментов использовалась реализация разложения Холецкого, представленная в пакете SCALAPACK библиотеки Intel MKL (метод pdpotrf). Все результаты получены на суперкомпьютере «Ломоносов»<ref name="Lom" />. Использовались процессоры Intel Xeon X5570 с пиковой производительностью в 94 Гфлопс, а также компилятор Intel с опцией –O2.
| |
| − | На рисунках показана эффективность реализации разложения Холецкого (случай использования нижних треугольников матриц) для размерности матрицы 80000, запуск проводился на 256 процессах.
| |
| − |
| |
| − | [[file:Cholesky CPU.png|thumb|center|700px|Рисунок 10. График загрузки CPU при выполнении разложения Холецкого]]
| |
| − |
| |
| − | На графике загрузки процессора видно, что почти все время работы программы уровень загрузки составляет около 50%. Это хорошая картина для программ, запущенных без использования технологии Hyper Threading.
| |
| − |
| |
| − | [[file:Cholesky FLOPS.png|thumb|center|700px|Рисунок 11. График операций с плавающей точкой в секунду при выполнении разложения Холецкого]]
| |
| − |
| |
| − | На Рисунке 11 показан график количества операций с плавающей точкой в секунду. Видно, что к концу каждой итерации число операций возрастает.
| |
| − | [[file:Cholesky L1.png|thumb|center|700px|Рисунок 12. График кэш-промахов L1 в секунду при работе разложения Холецкого]]
| |
| − |
| |
| − | На графике кэш-промахов первого уровня видно, что число промахов достаточно большое и находится на уровне 25 млн/сек в среднем по всем узлам.
| |
| − | [[file:Cholesky L3.png|thumb|center|700px|Рисунок 13. График кэш-промахов L3 в секунду при работе разложения Холецкого]]
| |
| − |
| |
| − | На графике кэш-промахов третьего уровня видно, что число промахов все еще достаточно большое и находится на уровне 1,5 млн/сек в среднем по всем узлам. Это указывает на то, что задача достаточно большая, и данные плохо укладываются в кэш-память.
| |
| − | [[file:Cholesky MemRead.png|thumb|center|700px|Рисунок 14. График количества чтений из оперативной памяти при работе разложения Холецкого]]
| |
| − |
| |
| − | На графике чтений из памяти на протяжении всего времени работы программы наблюдается достаточно интенсивная и не сильно изменяющаяся работа с памятью.
| |
| − | [[file:Cholesky MemWrite.png|thumb|center|700px|Рисунок 15. График количества записей в оперативную память при работе разложения Холецкого]]
| |
| − |
| |
| − | На графике записей в память видна периодичность: на каждой итерации к концу выполнения число записей в память достаточно сильно падает. Это коррелирует с возрастанием числа операций с плавающей точкой и может объясняться тем, что при меньшем числе записей в память программа уменьшает накладные расходы и увеличивает эффективность.
| |
| − | [[file:Cholesky Inf Bps.png|thumb|center|700px|Рисунок 16. График скорости передачи по сети Infiniband в байт/сек при работе разложения Холецкого]]
| |
| − |
| |
| − | На графике скорости передачи данных по сети Infiniband наблюдается достаточно интенсивное использование коммуникационной сети на каждой итерации. Причем к концу каждой итерации интенсивность передачи данных сильно возрастает. Это указывает на большую необходимость в обмене данными между процессами к концу итерации.
| |
| − | [[file:Cholesky Inf Pps.png|thumb|center|700px|Рисунок 17. График скорости передачи по сети Infiniband в пакетах/сек при работе разложения Холецкого]]
| |
| − |
| |
| − | На графике скорости передачи данных в пакетах в секунду наблюдается большая «кучность» показаний максимального минимального и среднего значений в сравнении с графиком скорости передачи в байт/сек. Это говорит о том, что, вероятно, процессы обмениваются сообщениями различной длины, что указывает на неравномерное распределение данных. Также наблюдается рост интенсивности использования сети к концу каждой итерации.
| |
| − | [[file:Cholesky LoadAVG.png|thumb|center|700px|Рисунок 18. График числа процессов, ожидающих вхождения в стадию счета (Loadavg), при работе разложения Холецкого]]
| |
| − | На графике числа процессов, ожидающих вхождения в стадию счета (Loadavg), видно, что на протяжении всей работы программы значение этого параметра постоянно и приблизительно равняется 8. Это свидетельствует о стабильной работе программы с восьмью процессами на каждом узле. Это указывает на рациональную и статичную загрузку аппаратных ресурсов процессами.
| |
| − | В целом, по данным системного мониторинга работы программы можно сделать вывод о том, что программа работала достаточно эффективно и стабильно. Использование памяти и коммуникационной среды достаточно интенсивное, что может стать фактором снижения эффективности при существенном росте размера задачи или же числа процессоров.
| |
| − | Для существующих параллельных реализаций характерно отнесение всего ресурса параллелизма на блочный уровень. Относительно низкая эффективность работы связана с проблемами внутри одного узла, следующим фактором является неоптимальное соотношение между «арифметикой» и обменами. Видно, что при некотором (довольно большом) оптимальном размере блока обмены влияют не так уж сильно.
| |
| | | | |
| | === Выводы для классов архитектур === | | === Выводы для классов архитектур === |
| − |
| |
| − | Как видно по показателям SCALAPACK на суперкомпьютерах, обмены при большом n хоть и уменьшают эффективность расчётов, но слабее, чем неоптимальность организации расчётов внутри одного узла. Поэтому, видимо, следует сначала оптимизировать не блочный алгоритм, а подпрограммы, используемые на отдельных процессорах: точечный метод Холецкого, перемножения матриц и др. подпрограммы. [[#Существующие реализации алгоритма|Ниже]] содержится информация о возможном направлении такой оптимизации.
| |
| − |
| |
| − | Вообще эффективность метода Холецкого для параллельных архитектур не может быть высокой. Это связано со следующим свойством информационной структуры алгоритма: если операции деления или вычисления выражений <math>a - bc</math> являются не только массовыми, но и параллельными, и потому их вычисления сравнительно легко выстраивать в конвейеры или распределять по устройствам, то операции извлечения квадратных корней являются узким местом алгоритма. Поэтому для эффективной реализации алгоритмов, столь же хороших по вычислительным характеристикам, как и метод квадратного корня, следует использовать не метод Холецкого, а его давно известную модификацию без извлечения квадратных корней — [[%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%A5%D0%BE%D0%BB%D0%B5%D1%86%D0%BA%D0%BE%D0%B3%D0%BE_(%D0%BD%D0%B0%D1%85%D0%BE%D0%B6%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%BD%D0%BE%D0%B3%D0%BE_%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D1%80%D0%B0%D0%B7%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F)#.5C.28LDL.5ET.5C.29_.D1.80.D0.B0.D0.B7.D0.BB.D0.BE.D0.B6.D0.B5.D0.BD.D0.B8.D0.B5|разложение матрицы в произведение <math>L D L^T</math>]]<ref>Krishnamoorthy A., Menon D. Matrix Inversion Using Cholesky Decomposition. 2013. eprint arXiv:1111.4144</ref>.
| |
| | | | |
| | === Существующие реализации алгоритма === | | === Существующие реализации алгоритма === |
| | | | |
| − | Точечный метод Холецкого реализован как в основных библиотеках программ отечественных организаций, так и в западных пакетах LINPACK, LAPACK, SCALAPACK и др.
| + | Существует масса реализаций метода Грама-Шмидта без реортогонализации, о которых говорится, например, [https://algowiki-project.org/ru/Участник:KibAndrey/Ортогонализация_Грама-Шмидта здесь]. Про реализации с реортогонализацией информации нет. |
| − |
| |
| − | При этом в отечественных реализациях, как правило, выполнены стандартные требования к методу с точки зрения ошибок округления, то есть, реализован режим накопления, и обычно нет лишних операций. Ряд старых отечественных реализаций использует для экономии памяти упаковку матриц <math>A</math> и <math>L</math> в одномерный массив.
| |
| − |
| |
| − | Реализация точечного метода Холецкого в современных западных пакетах обычно происходит из одной и той же реализации метода в LINPACK, а та использует пакет BLAS. В BLAS скалярное произведение реализовано без режима накопления, но это легко исправляется при желании.
| |
| − | | |
| − | Интересно, что в крупнейших библиотеках алгоритмов до сих пор предлагается именно разложение Холецкого, а более быстрый алгоритм LU-разложения без извлечения квадратных корней используется только в особых случаях (например, для трёхдиагональных матриц), в которых количество диагональных элементов уже сравнимо с количеством внедиагональных.
| |
| | | | |
| | == Литература == | | == Литература == |
| Строка 385: |
Строка 185: |
| | <references \> | | <references \> |
| | | | |
| − | [[en:Cholesky decomposition]]
| + | [[Категория:]] |
| − | | + | [[Категория:]] |
| − | [[Категория:Законченные статьи]] | |
| − | [[Категория:Разложения матриц]] | |
Автор: Г. А. Балыбердин
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Пусть [math]A = (a_1, ..., a_n)[/math] - вещественная матрица [math]n × n[/math], определитель которой не равен [math]0[/math]. Во многих приложениях требуется решать линейную систему [math]Ax=b[/math] c плохо-обусловленной матрицей [math]A[/math]. При решении данной задачи, чтобы не увеличивать число обусловленности матрицы [math]A[/math], ее можно представить в виде [math]A=QR[/math], где матрица [math]Q \in \mathbb{R}^{n×n}[/math] состоит из ортонормированных строк, а матрица [math] R \in \mathbb{R}^{n×n}[/math] является верхнетреугольной. В итоге мы получаем так называемую [math]QR[/math]-факторизацию.
Чтобы построить [math]QR[/math]-факторизацию можно воспользоваться процессом ортогонализации Грама-Шмидта[1], однако в условиях машинной арифметики, матрица [math]Q[/math] может получиться далекой от ортогональной.Чтобы этого избежать, на определенных итерациях нужно проводить процесс реортогонализации [2].
1.2 Математическое описание алгоритма
Исходные данные: квадратная матрица [math]A[/math] порядка [math]n[/math] (элементы [math]a_{ij}[/math]), определитель которой не равен [math]0[/math].
Вычисляемые данные: верхнетреугольная матрица [math]R[/math] порядка [math]n[/math] (элементы [math]r_{ij}[/math]), унитарная матрица [math]Q[/math] порядка [math]n[/math] (элементы [math]q_{ij}[/math]); выполняется соотношение [math]QR=A[/math].
Формулы процесса ортогонализации:
[math]
\begin{align}
& p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\
& q_{j} = p_{j} / ||p_{j}||_{2}, \\
& r_{ij} = q_{i}^{T} a_{j},\quad i = 1, \ldots , j - 1.\\
\end{align}
[/math]
Здесь [math]q_{i}, \, a_{i} [/math] столбцы матриц [math] Q, \, A [/math] соответственно.
На [math]m[/math]-ом шаге получаем [math]p_{m} \in \mathbb{R}^{n}[/math]. Если [math]||a_{m}||_{2}/||p_{m}||_{2} \gt k[/math], запускается процесс реортогонализации. [math]k[/math] произвольная и задает точность ортогональности матрицы [math]Q[/math]. В посвященной методу реортогонализации статье [3] [math]k[/math] рекомендуется брать равным [math]10[/math], однако приводятся примеры алгоритмов, где [math]k=\sqrt{2}[/math] или [math]k=\sqrt{5}[/math]. Мы исследуем [math]k=10[/math].
Суть процесса реортогонализации - это процесс ортогонализации Грама-Шмидта, примененный повторно к вектору [math]p_{m}[/math] на [math]m[/math]-оm шаге алгоритма. Более формально:
[math]
\begin{align}
& \tilde{p}_{m} = p_{m} - \sum_{i=1}^{m-1} q_{i} (q_{i}^{T} p_{m}), \\
& q_{m} = \tilde{p}_{m} / ||\tilde{p}_{m}||_{2}, \\
& \tilde{r}_{mj} = q_{j}^{T} p_{m}, \quad j = 1, \ldots , m - 1, \\
& r_{mj} = \tilde{r}_{mj} + r_{mj}^{0}, \quad j = 1, \ldots , m - 1, \\
& r_{mm} = ||\tilde{p}_{m}||_{2}.
\end{align}
[/math]
Здесь [math]\tilde{q}_{i}[/math] столбцы матриц [math] \tilde{Q}_{m}[/math], [math]r_{mj}^{0}[/math] - элементы матрицы [math]R[/math], вычисленные до реортогонализации.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма, если не требуется реортогонализация, состоит из вычисления:
- [math]\dfrac{n(n+1)}{2}[/math] скалярных произведений векторов, включая вычисление длины вектора;
- [math]\dfrac{(n-1)n}{2}[/math] умножений векторов на число.
На каждом шаге реортогонализации добавляется [math] j-1 [/math] вычислений скалярных произведений векторов на число и столько же умножений вектора на число. Здесь реортогонализация производится на [math]j[/math]-ом шаге. Однако сколько раз алгоритм будет реортогонализовывать вектора зависит от свойств матрицы.
1.4 Макроструктура алгоритма
Как записано и в описании ядра алгоритма, основную часть процесса составляют скалярные произведения векторов и умножения вектора на число:
[math]
\begin{align}
& p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\
& q_{j} = p_{j} / ||p_{j}||_{2}.
\end{align}
[/math]
как если алгоритм реортогонализует повторно вектора, так и без реортогонализаций.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения процесса следующая:
1. [math] q_1 = \frac{a_1}{||a_1||_2} [/math]
Далее для всех [math] i = 2, n [/math]:
2. [math] r_{ij} = q_{j}^{T} a_{i},\quad j = 1, \ldots , i - 1 [/math]
3. [math] p_{i} = a_{i} - \sum_{j=1}^{i-1} q_{j} r_{ij}[/math]
Если [math]||a_{i}||_{2}/||p_{i}||_{2} \gt k[/math], выполнить 4, 5, 6. Иначе перейти сразу к 7:
4. [math] r_{ij}^{0} = q_{j}^{T} p_{i},\quad j = 1, \ldots , i - 1 [/math]
5. [math] p_{i} = p_{i} - \sum_{j=1}^{i-1} q_{j} r_{ij}^{0}, \quad j = 1, \ldots , i - 1 [/math]
6. [math] r_{ij} = r_{ij}^{0} + r_{ij},\quad j = 1, \ldots , i - 1 [/math]
7. [math] r_{ii} = ||p_{i}||_{2} [/math]
8. [math] q_{i} = p_{i} / r_{ii} [/math]
Здесь (как и везде) под второй нормой подразумевается:
[math] ||x||_2 = \sqrt{x_1^2 + x_2^{2} + \ldots + x_n^2} [/math]
1.6 Последовательная сложность алгоритма
Для факторизации матрицы порядка n процессом Грама-Шмидта в последовательном варианте без реортогонализации требуется:
- [math]n[/math] извлечений квадратного корня,
- [math]n[/math] делений,
- [math](n-1)(n^2+2n-1)[/math] сложений (вычитаний),
- [math]n(n^2+2n-2)[/math] умножений.
Если реортогонализация работает на каждом шаге (чего никогда не случается, однако предположим худший случай), то количество всех операций удвоится. Таким образом, умножения и сложения (вычитания) составляют основную часть алгоритма.
При классификации по последовательной сложности, процесс ортогонализации Грама-Шмидта с реортогонализацией относится к алгоритмам с кубической сложностью.
1.7 Информационный граф
Опишем вершины информационного графа.
1. [math] a_i, \; i = 1 \ldots n [/math] — столбцы исходной матрицы [math] A [/math]; подаются на вход программе.
2. [math] N [/math] — операция взятия нормы вектора.
3. [math] div [/math] — операция деления вектора на число.
4. [math] Sc [/math] — операция взятия скалярного произведения двух векторов.
5. [math] F [/math] — операция вычитания из вектора произведение числа на вектор.
6. [math] + [/math] — операция суммирования двух чисел.
7. [math] r_{ij} [/math], [math] q_i, \; i = 1 \ldots n, \; j = 1 \ldots n [/math] — элементы матрицы [math] R [/math] и столбцы матрицы [math] Q [/math] соответственно; выходные данные программы.
Информационный граф построен для матрицы размерности [math] 3 [/math] при выполнении реортогонализации для третьего вектора.
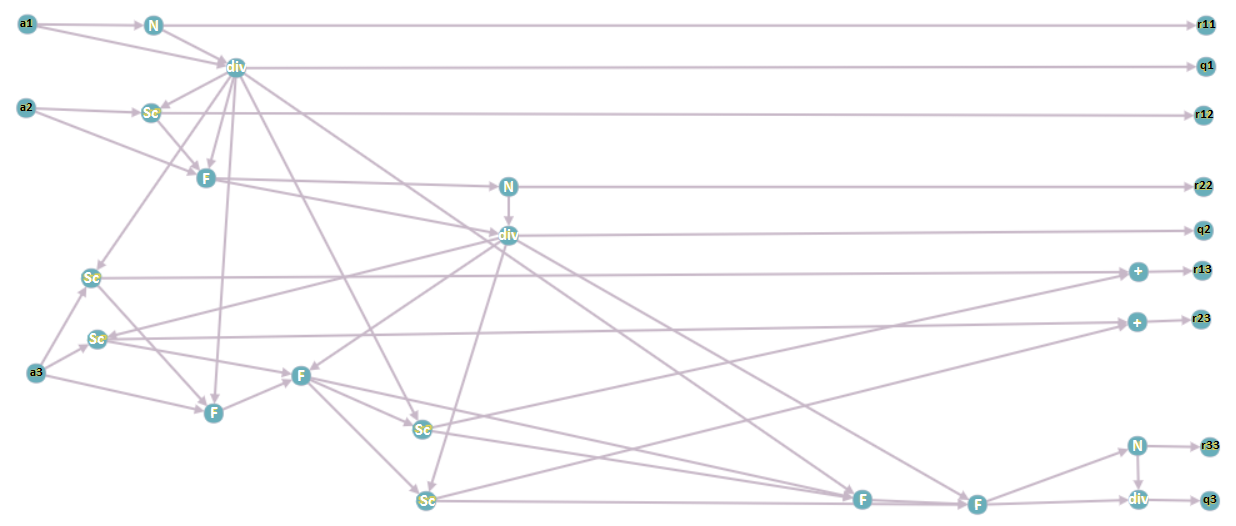
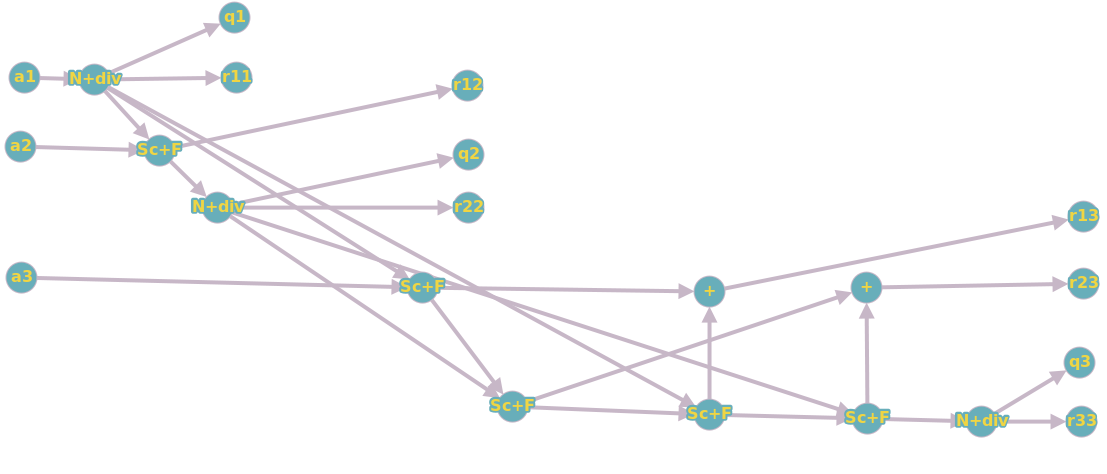
Если объединить вершины N и div, Sc и F (вершины будут означать суперпозиции соответствующих операций), то получится следующий, чуть более простой для понимания, граф:
1.8 Ресурс параллелизма алгоритма
В последовательной версии алгоритма двумя самыми трудоемкими операциями являются подсчет скалярных произведений и вычисление вектора, ортогонального предыдущим. Мы хотим добиться, чтобы каждый процессор считал "кусок" этих операций, однако также для ускорения работы программы нужно минимизировать число пересылок между процессорами. Пусть [math] k [/math] - количество процессоров. Предлагается разбить исходную матрицу [math] A [/math] на [math] k [/math] блоков по [math] \frac{n}{k} [/math] столбцов в каждом ([math] n [/math] - размерность задачи), тогда каждый процессор будет решать задачу на "своем подпространстве". Таким образом мы добьемся количества пересылок порядка [math] O(kn) [/math], и параллельная сложность алгоритма составит [math] O( \frac{n^3}{k} ) [/math].
1.9 Входные и выходные данные алгоритма
Входные данные: невырожденная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).
Объём входных данных: [math]n^2[/math].
Выходные данные: верхняя треугольная матрица [math]R[/math] (элементы [math]r_{ij}[/math]), унитарная матрица [math]Q[/math] (элементы [math]q_{ij}[/math]).
Объём выходных данных: [math]\frac{n (n + 1)}{2} + n^2[/math] (в силу треугольности матрицы [math]R[/math] достаточно хранить только ее ненулевые элементы).
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
число процессоров [math]2^k[/math], где k пробегает от 0 до 7;
размер матрицы [math]n^p[/math], где p пробегает от 8 до 12.
На следующем рисунке приведен график времени работы алгоритма (t) в зависимости от количества процессов (p) и размерности задачи (d):
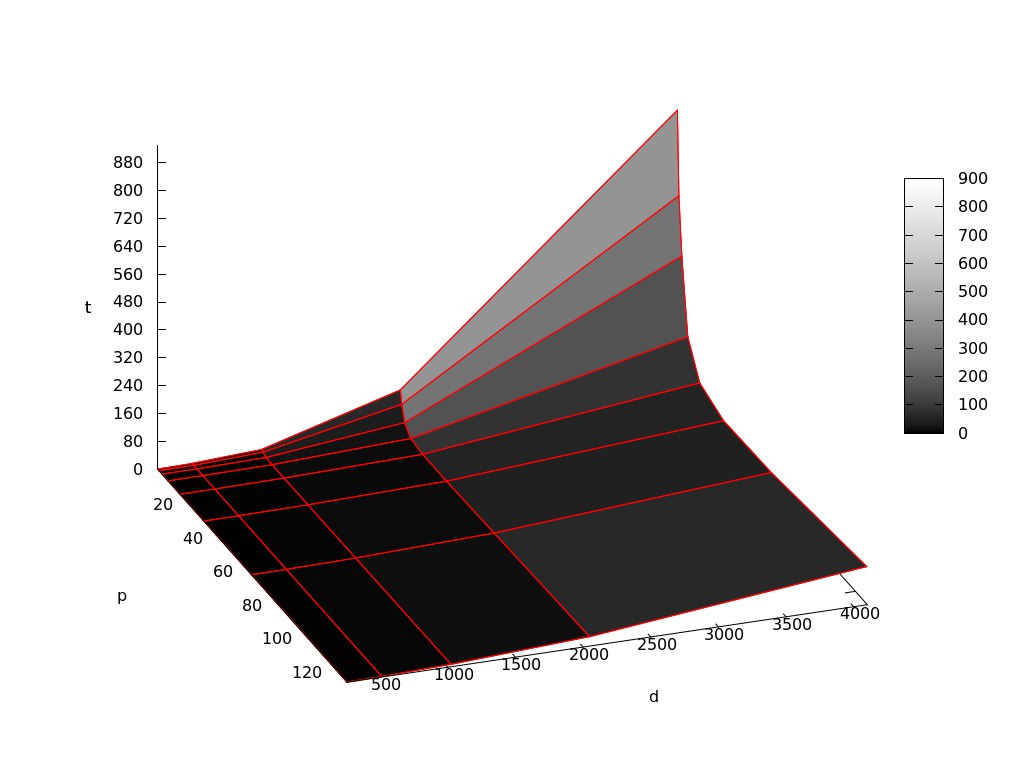
При увеличении количества процессов для задач разных (фиксированных) размерностей наблюдается общая закономерность: сначала время решения стремительно падает, потом не изменяется и далее начинает увеличиваться. Это связано с тем, что когда время работы программы падает, время пересылок много меньше времени работы процессов. При увеличении количества процессов увеличивается количество пересылок (и, следовательно, затраченное на них время) и в какой-то момент становится больше времени работы процессов.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Существует масса реализаций метода Грама-Шмидта без реортогонализации, о которых говорится, например, здесь. Про реализации с реортогонализацией информации нет.
3 Литература
<references \>
[[Категория:]]
[[Категория:]]
- ↑ Тыртышников Е.Е. Методы численного анализа // М.: 2006. 83 с.
- ↑ Luc Giraud, Julien Langou, Miroslav Rozložník, Jasper van den Eshof. Rounding error analysis of the classical Gram-Schmidt orthogonalization process // Springer-Verlag, 2005.
- ↑ Luc Giraud and Jilien Langou. A robust criterion for the modified Gram–Schmidt algorithm with selective reorthogonalization // Society for Industrial and Applied Mathematic, 2003.


