Участник:Kilkavteste 607/Генетический алгоритм: различия между версиями
| (не показано 11 промежуточных версий этого же участника) | |||
| Строка 32: | Строка 32: | ||
== Математическое описание алгоритма == | == Математическое описание алгоритма == | ||
| − | Для того чтобы реализовать генетический алгоритм, | + | Для того чтобы реализовать генетический алгоритм, необходимо решить, как именно у будет представлена начальная популяция, отдельная особь популяции, как будут реализованы процессы эволюции и какая функция подлежит оптимизации (функция приспособленности). |
| Строка 41: | Строка 41: | ||
::::<math> \\ F(x) = sin(x_1)\cdot sin(x_2)\cdot sin(x_3), </math> где <math> x = (x_1, x_2, x_3) </math> | ::::<math> \\ F(x) = sin(x_1)\cdot sin(x_2)\cdot sin(x_3), </math> где <math> x = (x_1, x_2, x_3) </math> | ||
| − | Будем пытаться найти ее минимум с помощью генетического алгоритма. Данная функция выгодна тем, что | + | Будем пытаться найти ее минимум с помощью генетического алгоритма. Данная функция выгодна тем, что заранее известен ее максимум, поэтому будет |
легко оценить, насколько хорошо алгоритм справился со своей задачей. Также она является многомерной, что позволит продемонстрировать плюсы ГА для решения задачи оптимизации многомерных функций. | легко оценить, насколько хорошо алгоритм справился со своей задачей. Также она является многомерной, что позволит продемонстрировать плюсы ГА для решения задачи оптимизации многомерных функций. | ||
2. Особь в популяции | 2. Особь в популяции | ||
| − | За особь в популяции выберем трехмерный вектор вещественных чисел (геномов). Числа будут иметь особенность (ведь их нужно как-то кодировать). Воспользуемся двоичным кодированием следующим образом: выберем интервал допустимых значений аргумента функции, в нашем случае будем рассматривать интервал <math> x_i \in [-\pi; \pi] </math>. Разобьем данный интервал на части, в зависимости от выбранной точности, в нашем случае, на <math> 2^{ | + | За особь в популяции выберем трехмерный вектор вещественных чисел (геномов). Числа будут иметь особенность (ведь их нужно как-то кодировать). Воспользуемся двоичным кодированием следующим образом: выберем интервал допустимых значений аргумента функции, в нашем случае будем рассматривать интервал <math> x_i \in [-\pi; \pi] </math>. Разобьем данный интервал на части, в зависимости от выбранной точности, в нашем случае, на <math> 2^{29} </math>. Таким образом, для кодирования нам потребуется 30 бит. Случайным образом выбирая число от <math> 0 </math> до <math> 2^{29} </math> получим номер интервала. За значение аргумента примем середину этого интервала. Таким образом мы получили представление вещественных чисел с помощью двоичного кода. Алгоритм взят из <ref > [https://basegroup.ru/community/articles/ga-math Генетические алгоритмы — математический аппарат] </ref>. |
3. Популяция | 3. Популяция | ||
| − | Начальная популяция будет состоять из <math> | + | Начальная популяция будет состоять из <math> 2000 </math> особей. Каждая особь представляет собой набор трех геномов, сформированных случайным образом, как указано в п.2. |
4. Скрещивание | 4. Скрещивание | ||
| Строка 59: | Строка 59: | ||
5. Мутация | 5. Мутация | ||
| − | В процессе мутации будут участвовать все особи. Это необходимо для поддержания разнообразия популяции. Случайным образом выбирается число от 0 до 100. Задается процент мутации. Если полученное число меньше или равно числу, равному проценту мутации, то мутация есть. Тогда выбирается еще одно случайное число от <math> 0 </math> до <math> | + | В процессе мутации будут участвовать все особи. Это необходимо для поддержания разнообразия популяции. Случайным образом выбирается число от 0 до 100. Задается процент мутации. Если полученное число меньше или равно числу, равному проценту мутации, то мутация есть. Тогда выбирается еще одно случайное число от <math> 0 </math> до <math> 29 </math>, и выбирается ген для мутации (меняем в побитовом представлении 0 на 1 или 1 на 0). Если полученное число больше числа, равного проценту мутации, то особь не мутирует. В нашем случае зададим процент мутации 20. |
6. Селекция | 6. Селекция | ||
| − | В реализуемом алгоритме потомки заменяют своих родителей. Заметим, что в большинстве реализаций селекция и скрещивание реализованы другим способом, например, в <ref >[https://m.habrahabr.ru/post/128704/ Генетический алгоритм. Просто о сложном] </ref>. Новое поколение тестируется на приспособленность | + | В реализуемом алгоритме потомки заменяют своих родителей. Заметим, что в большинстве реализаций селекция и скрещивание реализованы другим способом, например, в <ref >[https://m.habrahabr.ru/post/128704/ Генетический алгоритм. Просто о сложном] </ref>. Новое поколение тестируется на приспособленность: каждый раз сравнивается значение функции на новом << потомке >> с текущим минимальным и заменяется в случае нахождения меньшего значения. |
7. Критерий останова | 7. Критерий останова | ||
| − | За критерий останова взято ограниченное число поколений | + | За критерий останова взято ограниченное число поколений. |
| − | -- | + | == Вычислительное ядро алгоритма == |
| + | |||
| + | Вычислительное ядро алгоритма состоит из 3 частей: <br> | ||
| + | |||
| + | 1. Скрещивание: выбор двух родителей из массива популяции (выбираются два соседних представителя), генерация двух потомков (генерируется 2 случайных числа - точки разрыва "генома", потомки получаются путем обмена частями, полученными в ходе разрывов двух родительских геномов: первый потомок наследует начало генома первого родителя до точки разрыва и конец генома второго родителя после точки разрыва, второй потомок берет начало генома от второго родителя и конец от первого).<br> | ||
| + | |||
| + | 2. Мутация: оценка шанса мутации для каждого потомка (генерация случайного числа от 0 до 100, если число меньше числа, равного проценту мутации, то мутация есть), и возможная последующая мутация (генерация случайного числа от 0 до B - количества используемых битов в кодировании, затем изменение бита с этим номером в геноме на противоположный ему).<br> | ||
| − | + | 3. Проверка приспособленности: декодирование вещественных чисел (кодировка указана в п.1.1), вычисление значения функции приспособленности для каждого представителя популяции и сравнение полученного значения с сохраненным минимумом. | |
| − | |||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| + | |||
| + | 1. Генерация первого поколения. <br> | ||
| + | 2. Оценка приспособленности первого поколения и нахождение первичного минимума.<br> | ||
| + | 3. Эволюция:<br> | ||
| + | *Скрещивание | ||
| + | *Мутация | ||
| + | *Оценка приспособленности (поиск лучшего решения) | ||
| + | |||
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| + | |||
| + | Входные данные: <br> | ||
| + | * Функция приспособленности <math>F(x)</math> | ||
| + | * Размерность функции приспособленности <math>DIM</math> | ||
| + | * Интервал поиска минимума <math>[a,b]</math> | ||
| + | * Размер популяции <math>P</math> особей | ||
| + | * Количество рассматриваемых поколений <math>G</math> (критерий останова) | ||
| + | * Количество бит, используемых для кодирования вещественных чисел <math>B</math> | ||
| + | Генерация первого поколения: <br> | ||
| + | * Генерация вектора <math>population</math> размера <math>P*DIM</math> случайных целых чисел из интервала <math>[0, B]</math> | ||
| + | * Оценка приспособленности вектора <math>population</math>: нахождение первичного минимума <math>min</math> по всем особям популяции | ||
| + | Начало эволюции. Цикл по поколениям <math>g \in (0; G)</math> | ||
| + | * Цикл по размерности <math>dim \in [1; DIM]</math> | ||
| + | ** Цикл по особям в популяции <math>p \in [1; P]</math> | ||
| + | *** Скрещивание(); | ||
| + | *** Мутация(); | ||
| + | * Проверка приспособленности текущего поколения (поиск лучшего минимума) | ||
| + | Конец эволюции <br> | ||
| + | Выходные данные: <br> | ||
| + | * Минимальное значение функции, найденное алгоритмом <math>min</math> | ||
| + | |||
| + | |||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| + | |||
| + | Самыми частыми операциями в алгоритме являются генерация случайного числа, вычисление синуса, декодирование вещественного числа, обращение к памяти и запись числа в память. Посчитаем количество данных операций при последовательной реализации алгоритма. <br> | ||
| + | Обозначения: <math>P</math> - число особей в поколении, <math>DIM</math> - размерность функции приспособленности <math>F(x)</math>, <math>G</math> - количество поколений эволюции (итераций). | ||
| + | <math></math> <br> | ||
| + | |||
| + | 1. Генерация случайного числа. Для генерации первого поколения необходимо <math>P\cdot DIM</math> операций. Для скрещиваний в каждом поколении нужно <math>P\cdot DIM</math> генераций случайных чисел. Для мутаций в каждом поколении минимум <math>P\cdot DIM</math> генераций, максимум <math>2\cdot P \cdot DIM</math>. Итого по всем поколениям: <math>P + P \cdot DIM \cdot G + 2 \cdot P \cdot DIM \cdot G = O(PG)</math> операций генерации случайных чисел. Генерация случайного числа программно равна <math>3</math> операциям умножения, что не меняет ранее найденный порядок сложности. | ||
| + | |||
| + | 2. Вычисление синуса. На каждой популяции нужно вычислить <math>P \cdot DIM </math>. Итого <math>G \cdot P \cdot DIM = O(PG)</math> операций. <br> | ||
| + | |||
| + | 3. Декодирование. Количество операций декодирования равно количеству вычисления синуса. По сложности операция декодирования сводится к двум операциям умножения. Итого получим <math>2 \cdot G \cdot P \cdot DIM = O(PG)</math> операций умножения. <br> | ||
| + | |||
| + | 4. Обращение в память. Для работы алгоритма нужно <math>2P \cdot DIM</math> операций на начальной популяции. Так же для реализации скрещивания <math>P\cdot DIM </math> операций, для мутации не более <math>P \cdot DIM</math> обращений в память и для проверки приспособленности <math>P \cdot DIM</math> операций. Итого для всех <math>G</math> популяций <math> 2P \cdot DIM + G \cdot P \cdot DIM + G \cdot P \cdot DIM + G \cdot P \cdot DIM = O(PG)</math> операций обращения в память. <br> | ||
| + | |||
| + | 5. Запись числа в память. Для генерации начальной популяции <math>P\cdot DIM</math> операций, для скрещиваний на каждой итерации <math>P \cdot DIM</math> операций, для мутации не более <math>P \cdot DIM</math> операций. Для записи максимума требуется <math>1 + G</math> операций. Итого <math>O((P+1)G)</math> операций записи нового числа в память. | ||
| + | |||
| + | |||
| + | Итого получаем сложность порядка <math>O((P+1)G)</math>. | ||
| + | |||
== Информационный граф == | == Информационный граф == | ||
| + | Приведем информационный граф макроструктуры алгоритма, тем самым простейшие операции не загромоздят рисунок и основная идея будет понятна. Алгоритмы-узлы подробно описаны в пунктах 1.1-1.3, их самостоятельная реализация не составляет труда. | ||
| + | Данный граф приведен для фиксированного набора данных: размерности минимизируемой функции: <math>DIM = 2</math>, количества особей в популяции: <math>P = 3</math> и числа итераций: <math>G = 4</math>. <br> | ||
| + | [[Файл:Graph_genetic.jpg|700px]] | ||
| + | |||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| + | Как можно заметить по информационному графу, приведенному в п.1.7, ресурсом параллелизма может быть количество итераций, при условии, что каждый узел в любой момент времени имеет доступ к входным данным - минимизируемой функции, а также к ее текущему минимальному значению. Также ресурсом параллелизма может являться размер популяции: вектор особей можно разделить между процессами и подвергнуть каждую часть независимому эволюционному процессу. | ||
| + | |||
| + | Для достижения более качественного поиска минмимума можно реализовать периодический обмен (раз в несколько итераций) лучшими особями между процессами по принципу "все со всеми". Также коммуникация между процессами должна осуществлять выбор минимального значения среди всех найденных минимумов на разных процессорах. | ||
| + | |||
| + | Необходимо заметить, что алгоритм поиска минимума, обозначенный на графе в п.1.7 узлом min нежно-зеленого цвета, также представляет собой ресурс параллелизма, однако параллельная реализация данного узла будет слишком трудозатратной из-за необходимости множественного обмена между процессорами по принципу "все со всеми" большое число раз. | ||
| + | |||
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
| + | На вход алгоритму необходимо подать минимизируемую функцию <math>F(x)</math> с указанием ее размерности. На выходе пользователь получает минимальное значение функции. | ||
| + | |||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| Строка 88: | Строка 153: | ||
== Возможные способы и особенности параллельной реализации алгоритма == | == Возможные способы и особенности параллельной реализации алгоритма == | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| + | Проведем исследование масштабируемости реализации алгоритма. Параллелизм проводился по числу итераций. Исследование проводилось на суперкомпьютере "Ломоносов"<ref name="Lom">Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.</ref> [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета]. | ||
| + | |||
| + | Набор и границы значений изменяемых параметров запуска реализации алгоритма:<br> | ||
| + | * число процессоров: <math>2^n</math>, n = 1,...,7 | ||
| + | * число итераций: <math>2^p</math>, p = 7,..., 14 | ||
| + | |||
| + | В результате экспериментов получен диапазон эффективности реализации алгоритма: | ||
| + | |||
| + | * минимальная эффективность реализации: 0.77 | ||
| + | * максимальная эффективность реализации: 0.9996 | ||
| + | |||
| + | На следующих рисунках приведены графики зависимости времени и эффективности от числа процессов и числа итераций.<br> | ||
| + | [[Файл:Time_genetic.jpg|500px]] [[Файл:Efficiency_genetic.jpg|500px]] | ||
| + | |||
| + | На графиках заметно, что при увеличении процессоров до 64 начинает незначительно падать эффективность, засчет увеличения узлов, с которыми происходит обмен данными по принципу "все со всеми". Однако падение эффективности снижается при увеличении числа итераций, так как затраты на коммуникацию становятся значительно меньше, чем на решение самой задачи. Также не лишним будет заметить, что параллельная работа значительно экономит время пользователя, уменьшая его практически в 2 раза при увеличении числа узлов в 2 раза, хоть и не всегда эффективно используя ресурсы. | ||
| + | |||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
== Выводы для классов архитектур == | == Выводы для классов архитектур == | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| + | Генетический алгоритм реализован во многих пакетах программ, например, в библиотеке scipy языка Python, как алгоритм оптимизации. | ||
= Литература = | = Литература = | ||
Текущая версия на 19:52, 30 ноября 2017
Генетический алгоритм
Автор описания: А. С. Горбатова
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Генети́ческий алгори́тм (англ. genetic algorithm) — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, аналогичных естественному отбору в природе. Является разновидностью эволюционных вычислений, с помощью которых решаются оптимизационные задачи с использованием методов естественной эволюции, таких как наследование, мутации, отбор и кроссинговер. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.
Можно выделить следующие этапы генетического алгоритма:
- Задание целевой функции (функции приспособленности) для особей популяции
- Создание начальной популяции
- Цикл (пока не выполнится критерий останова):
- Размножение (скрещивание)
- Мутирование
- [Кросиннговер] - по желанию
- Вычисление значения целевой функции для всех особей, полученных в результате предыдущих этапов цикла
- Формирование нового поколения (селекция)
Критериями останова могут служить:
- нахождение глобального, либо субоптимального решения;
- исчерпание числа поколений, отпущенных на эволюцию;
- исчерпание времени, отпущенного на эволюцию.
Необходимо заметить, что не существует общепринятых стандартов реализации генетического алгоритма, поэтому каждый может самостоятельно решить, как именно он будет реализовывать конкретный этап эволюционного процесса.
1.2 Математическое описание алгоритма
Для того чтобы реализовать генетический алгоритм, необходимо решить, как именно у будет представлена начальная популяция, отдельная особь популяции, как будут реализованы процессы эволюции и какая функция подлежит оптимизации (функция приспособленности).
1. Функция приспособленности
Для учебной задачи выберем простую трехмерную функцию :
- [math] \\ F(x) = sin(x_1)\cdot sin(x_2)\cdot sin(x_3), [/math] где [math] x = (x_1, x_2, x_3) [/math]
Будем пытаться найти ее минимум с помощью генетического алгоритма. Данная функция выгодна тем, что заранее известен ее максимум, поэтому будет легко оценить, насколько хорошо алгоритм справился со своей задачей. Также она является многомерной, что позволит продемонстрировать плюсы ГА для решения задачи оптимизации многомерных функций.
2. Особь в популяции
За особь в популяции выберем трехмерный вектор вещественных чисел (геномов). Числа будут иметь особенность (ведь их нужно как-то кодировать). Воспользуемся двоичным кодированием следующим образом: выберем интервал допустимых значений аргумента функции, в нашем случае будем рассматривать интервал [math] x_i \in [-\pi; \pi] [/math]. Разобьем данный интервал на части, в зависимости от выбранной точности, в нашем случае, на [math] 2^{29} [/math]. Таким образом, для кодирования нам потребуется 30 бит. Случайным образом выбирая число от [math] 0 [/math] до [math] 2^{29} [/math] получим номер интервала. За значение аргумента примем середину этого интервала. Таким образом мы получили представление вещественных чисел с помощью двоичного кода. Алгоритм взят из [1].
3. Популяция
Начальная популяция будет состоять из [math] 2000 [/math] особей. Каждая особь представляет собой набор трех геномов, сформированных случайным образом, как указано в п.2.
4. Скрещивание
Для скрещивания берем 2 родителей - соседних особей по популяции (первый со вторым, третий с четвертым и так далее). После этого случайным образом определяется точка разрыва генома, затем от первого родителя берется первая часть нового генома (до точки разрыва), от второго - вторая. Таким образом получим первого потомка. Получим второго потомка, также определив случайным образом точку разрыва, взяв от второго родителя гены до точки разрыва, от первого - после. Потомки заменят в новой популяции своих родителей. (Очень семейная реализация, придумана лично мной.)
5. Мутация
В процессе мутации будут участвовать все особи. Это необходимо для поддержания разнообразия популяции. Случайным образом выбирается число от 0 до 100. Задается процент мутации. Если полученное число меньше или равно числу, равному проценту мутации, то мутация есть. Тогда выбирается еще одно случайное число от [math] 0 [/math] до [math] 29 [/math], и выбирается ген для мутации (меняем в побитовом представлении 0 на 1 или 1 на 0). Если полученное число больше числа, равного проценту мутации, то особь не мутирует. В нашем случае зададим процент мутации 20.
6. Селекция
В реализуемом алгоритме потомки заменяют своих родителей. Заметим, что в большинстве реализаций селекция и скрещивание реализованы другим способом, например, в [2]. Новое поколение тестируется на приспособленность: каждый раз сравнивается значение функции на новом << потомке >> с текущим минимальным и заменяется в случае нахождения меньшего значения.
7. Критерий останова
За критерий останова взято ограниченное число поколений.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит из 3 частей:
1. Скрещивание: выбор двух родителей из массива популяции (выбираются два соседних представителя), генерация двух потомков (генерируется 2 случайных числа - точки разрыва "генома", потомки получаются путем обмена частями, полученными в ходе разрывов двух родительских геномов: первый потомок наследует начало генома первого родителя до точки разрыва и конец генома второго родителя после точки разрыва, второй потомок берет начало генома от второго родителя и конец от первого).
2. Мутация: оценка шанса мутации для каждого потомка (генерация случайного числа от 0 до 100, если число меньше числа, равного проценту мутации, то мутация есть), и возможная последующая мутация (генерация случайного числа от 0 до B - количества используемых битов в кодировании, затем изменение бита с этим номером в геноме на противоположный ему).
3. Проверка приспособленности: декодирование вещественных чисел (кодировка указана в п.1.1), вычисление значения функции приспособленности для каждого представителя популяции и сравнение полученного значения с сохраненным минимумом.
1.4 Макроструктура алгоритма
1. Генерация первого поколения.
2. Оценка приспособленности первого поколения и нахождение первичного минимума.
3. Эволюция:
- Скрещивание
- Мутация
- Оценка приспособленности (поиск лучшего решения)
1.5 Схема реализации последовательного алгоритма
Входные данные:
- Функция приспособленности [math]F(x)[/math]
- Размерность функции приспособленности [math]DIM[/math]
- Интервал поиска минимума [math][a,b][/math]
- Размер популяции [math]P[/math] особей
- Количество рассматриваемых поколений [math]G[/math] (критерий останова)
- Количество бит, используемых для кодирования вещественных чисел [math]B[/math]
Генерация первого поколения:
- Генерация вектора [math]population[/math] размера [math]P*DIM[/math] случайных целых чисел из интервала [math][0, B][/math]
- Оценка приспособленности вектора [math]population[/math]: нахождение первичного минимума [math]min[/math] по всем особям популяции
Начало эволюции. Цикл по поколениям [math]g \in (0; G)[/math]
- Цикл по размерности [math]dim \in [1; DIM][/math]
- Цикл по особям в популяции [math]p \in [1; P][/math]
- Скрещивание();
- Мутация();
- Цикл по особям в популяции [math]p \in [1; P][/math]
- Проверка приспособленности текущего поколения (поиск лучшего минимума)
Конец эволюции
Выходные данные:
- Минимальное значение функции, найденное алгоритмом [math]min[/math]
1.6 Последовательная сложность алгоритма
Самыми частыми операциями в алгоритме являются генерация случайного числа, вычисление синуса, декодирование вещественного числа, обращение к памяти и запись числа в память. Посчитаем количество данных операций при последовательной реализации алгоритма.
Обозначения: [math]P[/math] - число особей в поколении, [math]DIM[/math] - размерность функции приспособленности [math]F(x)[/math], [math]G[/math] - количество поколений эволюции (итераций).
[math][/math]
1. Генерация случайного числа. Для генерации первого поколения необходимо [math]P\cdot DIM[/math] операций. Для скрещиваний в каждом поколении нужно [math]P\cdot DIM[/math] генераций случайных чисел. Для мутаций в каждом поколении минимум [math]P\cdot DIM[/math] генераций, максимум [math]2\cdot P \cdot DIM[/math]. Итого по всем поколениям: [math]P + P \cdot DIM \cdot G + 2 \cdot P \cdot DIM \cdot G = O(PG)[/math] операций генерации случайных чисел. Генерация случайного числа программно равна [math]3[/math] операциям умножения, что не меняет ранее найденный порядок сложности.
2. Вычисление синуса. На каждой популяции нужно вычислить [math]P \cdot DIM [/math]. Итого [math]G \cdot P \cdot DIM = O(PG)[/math] операций.
3. Декодирование. Количество операций декодирования равно количеству вычисления синуса. По сложности операция декодирования сводится к двум операциям умножения. Итого получим [math]2 \cdot G \cdot P \cdot DIM = O(PG)[/math] операций умножения.
4. Обращение в память. Для работы алгоритма нужно [math]2P \cdot DIM[/math] операций на начальной популяции. Так же для реализации скрещивания [math]P\cdot DIM [/math] операций, для мутации не более [math]P \cdot DIM[/math] обращений в память и для проверки приспособленности [math]P \cdot DIM[/math] операций. Итого для всех [math]G[/math] популяций [math] 2P \cdot DIM + G \cdot P \cdot DIM + G \cdot P \cdot DIM + G \cdot P \cdot DIM = O(PG)[/math] операций обращения в память.
5. Запись числа в память. Для генерации начальной популяции [math]P\cdot DIM[/math] операций, для скрещиваний на каждой итерации [math]P \cdot DIM[/math] операций, для мутации не более [math]P \cdot DIM[/math] операций. Для записи максимума требуется [math]1 + G[/math] операций. Итого [math]O((P+1)G)[/math] операций записи нового числа в память.
Итого получаем сложность порядка [math]O((P+1)G)[/math].
1.7 Информационный граф
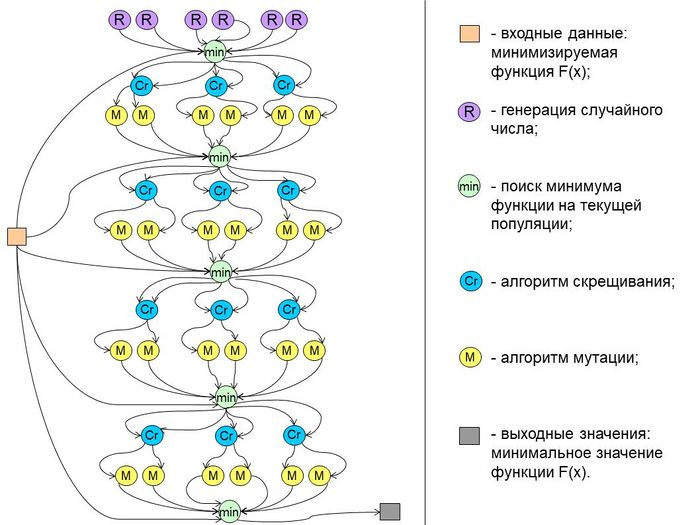
Приведем информационный граф макроструктуры алгоритма, тем самым простейшие операции не загромоздят рисунок и основная идея будет понятна. Алгоритмы-узлы подробно описаны в пунктах 1.1-1.3, их самостоятельная реализация не составляет труда.
Данный граф приведен для фиксированного набора данных: размерности минимизируемой функции: [math]DIM = 2[/math], количества особей в популяции: [math]P = 3[/math] и числа итераций: [math]G = 4[/math].
1.8 Ресурс параллелизма алгоритма
Как можно заметить по информационному графу, приведенному в п.1.7, ресурсом параллелизма может быть количество итераций, при условии, что каждый узел в любой момент времени имеет доступ к входным данным - минимизируемой функции, а также к ее текущему минимальному значению. Также ресурсом параллелизма может являться размер популяции: вектор особей можно разделить между процессами и подвергнуть каждую часть независимому эволюционному процессу.
Для достижения более качественного поиска минмимума можно реализовать периодический обмен (раз в несколько итераций) лучшими особями между процессами по принципу "все со всеми". Также коммуникация между процессами должна осуществлять выбор минимального значения среди всех найденных минимумов на разных процессорах.
Необходимо заметить, что алгоритм поиска минимума, обозначенный на графе в п.1.7 узлом min нежно-зеленого цвета, также представляет собой ресурс параллелизма, однако параллельная реализация данного узла будет слишком трудозатратной из-за необходимости множественного обмена между процессорами по принципу "все со всеми" большое число раз.
1.9 Входные и выходные данные алгоритма
На вход алгоритму необходимо подать минимизируемую функцию [math]F(x)[/math] с указанием ее размерности. На выходе пользователь получает минимальное значение функции.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Проведем исследование масштабируемости реализации алгоритма. Параллелизм проводился по числу итераций. Исследование проводилось на суперкомпьютере "Ломоносов"[3] Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров: [math]2^n[/math], n = 1,...,7
- число итераций: [math]2^p[/math], p = 7,..., 14
В результате экспериментов получен диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации: 0.77
- максимальная эффективность реализации: 0.9996
На следующих рисунках приведены графики зависимости времени и эффективности от числа процессов и числа итераций.
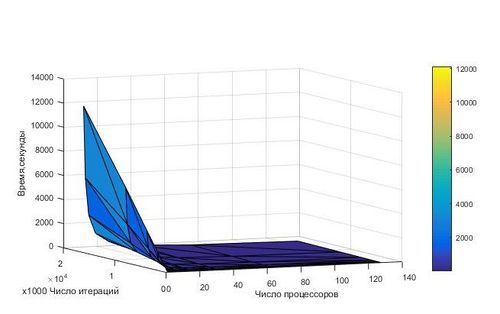
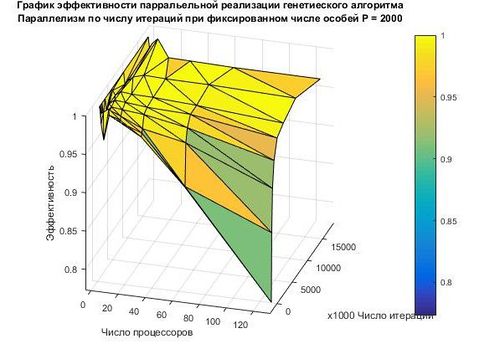
На графиках заметно, что при увеличении процессоров до 64 начинает незначительно падать эффективность, засчет увеличения узлов, с которыми происходит обмен данными по принципу "все со всеми". Однако падение эффективности снижается при увеличении числа итераций, так как затраты на коммуникацию становятся значительно меньше, чем на решение самой задачи. Также не лишним будет заметить, что параллельная работа значительно экономит время пользователя, уменьшая его практически в 2 раза при увеличении числа узлов в 2 раза, хоть и не всегда эффективно используя ресурсы.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Генетический алгоритм реализован во многих пакетах программ, например, в библиотеке scipy языка Python, как алгоритм оптимизации.
3 Литература
- ↑ Генетические алгоритмы — математический аппарат
- ↑ Генетический алгоритм. Просто о сложном
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.