Участник:Rpu6/Алгоритм построения приближённого решения нерегулярно вырождающегося эллиптического дифференциального уравнения: различия между версиями
Rpu6 (обсуждение | вклад) |
Rpu6 (обсуждение | вклад) |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 2: | Строка 2: | ||
| name = Алгоритм построения приближённого решения нерегулярно вырождающегося эллиптического дифференциального уравнения | | name = Алгоритм построения приближённого решения нерегулярно вырождающегося эллиптического дифференциального уравнения | ||
| serial_complexity = <math>O(KN\mathrm{max}(K, N))</math> | | serial_complexity = <math>O(KN\mathrm{max}(K, N))</math> | ||
| − | | pf_height = <math> | + | | pf_height = <math>O(\mathrm{max}(K, N^2))</math> |
| − | | pf_width = <math> | + | | pf_width = <math>O(KN)</math> |
| input_data = <math>KN + 2N</math> | | input_data = <math>KN + 2N</math> | ||
| output_data = <math>KN</math> | | output_data = <math>KN</math> | ||
| Строка 35: | Строка 35: | ||
c(y)=\sum_{n=1}^{N}c_ny^n, | c(y)=\sum_{n=1}^{N}c_ny^n, | ||
f_k(y)=\sum_{n=0}^{N}f_{kn}y^n.</math> | f_k(y)=\sum_{n=0}^{N}f_{kn}y^n.</math> | ||
| − | Разложение можно проводить по аналогии с разложением в ряд Фурье, но с использованием полиномов Лежандра. | + | Разложение можно проводить по аналогии с разложением в ряд Фурье, но с использованием полиномов Лежандра, Чебышёва, или той же тригонометрической системы функций. Можно использовать интерполяционные полиномы. |
3. Введём в рассмотрение числа: | 3. Введём в рассмотрение числа: | ||
| Строка 88: | Строка 88: | ||
Будем оценивать количество операций умножения вещественных чисел. Произведём оценку отдельно для каждого шага алгоритма.<br> | Будем оценивать количество операций умножения вещественных чисел. Произведём оценку отдельно для каждого шага алгоритма.<br> | ||
| − | 1. <math>(K + 1) | + | 1. <math>(K + 1)KN</math> умножение для вычисления всех <math>f_k(y_j)</math> (N возникает в силу необходимости вычислять функцию в каждой точке сетки по y), |
| − | <math>((N + 1)N + 1)K</math> операций для вычисления <math>f_{kn}</math> (считаем, что значения гармоник и полиномов Лежандра известны заранее), | + | <math>((N + 1)N + 1)K</math> операций для вычисления <math>f_{kn}</math> (считаем, что значения гармоник и полиномов Лежандра известны заранее, |
| + | учитываем равенство некоторых скалярных произведений при вычислении), | ||
<math>2((N + 1)N + 1)</math> операций для вычисления <math>a_n, c_n</math>. | <math>2((N + 1)N + 1)</math> операций для вычисления <math>a_n, c_n</math>. | ||
2. Для вычисления n-го коэффициента требуется <math>5 + 3(n-1)</math> операций, для вычисления всех коэффициентов - | 2. Для вычисления n-го коэффициента требуется <math>5 + 3(n-1)</math> операций, для вычисления всех коэффициентов - | ||
| Строка 95: | Строка 96: | ||
коррекция <math>\varphi_k(y_j)</math> требует <math>N + 2</math> операции, построение самих функций - <math>N(2N)=2N^2</math> операций. Это всё нужно проделать <math>K</math> раз.<br> | коррекция <math>\varphi_k(y_j)</math> требует <math>N + 2</math> операции, построение самих функций - <math>N(2N)=2N^2</math> операций. Это всё нужно проделать <math>K</math> раз.<br> | ||
3. Вычисление значения функции в узле сетки стоит <math>3K</math> операций умножения. Это нужно проделать в <math>KN</math> узлах.<br> | 3. Вычисление значения функции в узле сетки стоит <math>3K</math> операций умножения. Это нужно проделать в <math>KN</math> узлах.<br> | ||
| − | Выделим главный член асимптотики по всем шагам: <math>KN^2 + 3,5KN^2 + 3K^2N=O(KN\mathrm{max}(K,N)).</math><br> | + | Выделим главный член асимптотики по всем шагам: <math>K^2N + KN^2 + 3,5KN^2 + 3K^2N=O(KN\mathrm{max}(K,N)).</math><br> |
Если положить <math>K=N</math>, то сложность алгоритма имеет порядок <math>O(N^3)</math>. | Если положить <math>K=N</math>, то сложность алгоритма имеет порядок <math>O(N^3)</math>. | ||
== Информационный граф == | == Информационный граф == | ||
| + | Приведём информационные графы для каждой части алгоритма отдельно (иначе граф чрезмерно громоздкий).<br> | ||
| + | 1. Построение коэффициентов <math>f_{kn}</math> по функции <math>f(x,y)</math> (тут и далее K = N = 3).<br> | ||
| + | [[File:F-T-f.png|500px]]<br> | ||
| + | 2. Построение коэффициентов <math>a_n, c_n</math> осуществляется по общей схеме.<br> | ||
| + | [[File:T-g.png|400px]]<br> | ||
| + | 3. Построение коэффициентов <math>\eta_{kn}, \varphi_{kn}</math> при фиксированном k.<br> | ||
| + | [[File:T-phi-eta.png|500px]]<br> | ||
| + | 4. Построение самих функций <math>\eta_k(y), \varphi_k(y)</math>.<br> | ||
| + | [[File:S-phi-eta.png|400px]]<br> | ||
| + | 5. Построение решения в некоторой точке <math>(x,y)</math>.<br> | ||
| + | [[File:S-u.png|500px]]<br> | ||
| + | Макроструктуру всего алгоритма можно описать следующим графом:<br> | ||
| + | [[File:Regularization-General-Graph.png|600px]] | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| + | Будем оценивать параллельную сложность алгоритма в терминах блоков из пункта 1.7. | ||
| + | Предполагаем для простоты, что любые данные, помеченные промежуточными на общем графе, доступны с любой параллельной ветви | ||
| + | (для обеспечения этого в программе потребуется синхронизация на промежуточных этапах с обменом информацией). | ||
| + | Длинные операции суммирования считаем выполняемыми последовательно (без параллелизма). На практике это имеет смысл в силу малой сложности суммы. | ||
| + | Распараллеливание только замедлит программу за счёт обмена данными.<br> | ||
| + | Итак, в первом блоке операций каждый коэффициент Фурье в каждой точке может быть вычислен независимо от других. Числа <math>f_{kn}</math> также вычисляются независимо при различных K и N. | ||
| + | В этом случае параллельная сложность - <math>O(\mathrm{max}(K,N))</math>. | ||
| + | Допустив суммирование сдваиванием, получим <math>O(\log_2 \mathrm{max}(K,N))</math>. Параллелизм по K и N - массовый, в случае суммирования сдваиванием имеем дополнительно скошенный параллелизм.<br> | ||
| + | Вычисление <math>a_n, c_n</math> не зависит от <math>f_{kn}</math>, его можно выполнить параллельно (конечный параллелизм). Сами же вычисления за счёт массового параллелизма по N упрощаются | ||
| + | до параллельной сложности <math>O(N)</math>.<br> | ||
| + | Третий блок, как видно из общего графа, допускает массовый параллелизм по K. Однако, внутренние вычисления, как видно из третьего графа, весьма запутанные и не допускают координатного параллелизма | ||
| + | (достаточно заметить в формулах, что каждый следующий n+1-й коэффициент требует знания всех предыдущих для вычисления). В этом случае параллельная сложность - <math>O(N^2)</math>. | ||
| + | С использованием скошенного параллелизма можно потенциально сократить параллельную сложность до <math>O(N)</math>, если все коэффициенты будут считаться параллельно. | ||
| + | Но в этом случае после вычисления каждого следующего коэффициента, необходимо передать его в параллельные ветви, вычисляющие другие (со старшими номерами). | ||
| + | Это на практике потребует существенных временных расходов на передачу данных и синхронизацию.<br> | ||
| + | Вычисление же <math>\eta_k(y), \stackrel{\circ}{\varphi}_k(y)</math> независимо в каждой точке y и при каждом индексе k. Массовый параллелизм. Параллельная сложность - <math>O(N)</math>. | ||
| + | Коррекция <math>\stackrel{\circ}{\varphi}_k(y)</math> при этом имеет параллельную сложность <math>O(1)</math>.<br> | ||
| + | И, наконец, вычисление решение можно вести независимо в каждой точке (массовый параллелизм). Параллельная сложность - <math>O(K)</math>, в случае суммирования сдваиванием - <math>O(\log_2 K)</math>.<br> | ||
| + | Итоговая параллельная сложность алгоритма: <math>O(\mathrm{max}(K, N^2))</math>. Использование суммирования сдваиванием и указанного подхода в третьем блоке позволяют уменьшить параллельную сложность до | ||
| + | <math>O(\mathrm{max}(\log_2 K, N))</math>. | ||
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
| + | На вход алгоритм получает заданные на сетке функции <math>f(x,y), a(y), c(y)</math> (<math>(K+2)N</math> вещественных чисел). | ||
| + | На выходе у алгоритма заданное на сетке решение <math>u(x,y)</math> (<math>KN</math> вещественных чисел). Используется сетка, объявленная в пункте 1.5. | ||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| Строка 109: | Строка 145: | ||
== Возможные способы и особенности параллельной реализации алгоритма == | == Возможные способы и особенности параллельной реализации алгоритма == | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| + | [[File:Regularization-Graphic-K=P.PNG|мини|1. График времени работы для слабой масштабируемости]] | ||
| + | [[File:Regularization-Graphic-K=const,T.PNG|мини|2. График времени работы для сильной масштабируемости]] | ||
| + | [[File:Regularization-Graphic-K=const,E.PNG|мини|3. График эффективности распараллеливания для сильной масштабируемости]] | ||
| + | Будем рассматривать масштабируемость реализации алгоритма при некоторых ограничениях. Опираясь на пункт 1.8, заметим, что на шагах алгоритма 1 и 3 характер параллелизма по N имеет тот же характер, что и по K. | ||
| + | Кроме того, на шаге 2, как было замечено, без использования затратных в организации методов распараллеливания, параллельная сложность по N равна <math>O(N^2)</math> и не может быть уменьшена. | ||
| + | Руководствуясь этими аргументами, положим во всех текстах <math>N=const=2048</math> и исследуем ресурс параллелизма по K.<br> | ||
| + | Все результаты запусков были получены на суперкомпьютере «Ломоносов»<ref>https://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%BC%D0%BE%D0%BD%D0%BE%D1%81%D0%BE%D0%B2_(%D1%81%D1%83%D0%BF%D0%B5%D1%80%D0%BA%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80)</ref><ref>http://users.parallel.ru/wiki/pages/22-config</ref> (ссылка на технические характеристики в литературе). | ||
| + | Отметим следующие свойства, которые должны следовать из свойств алгоритма:<br> | ||
| + | 1. При P < K (P - количество процессоров) имеет место сильная масштабируемость. Действительно, не изменяя K, мы можем увеличить количество процессоров P (P < K). | ||
| + | В этом случае производительность должна пропорционально сократиться (см. пункт 1.8).<br> | ||
| + | 2. При P = K имеет место слабая масштабируемость, ибо при P > K не удастся равномерно загрузить все узлы работой и некоторые узлы будут бездействовать, однако, | ||
| + | в случае повышения K, вы вновь сможем увеличить количество процессоров так, что время работы программы на этапах 1 и 2 останется неизменным, | ||
| + | а на этапе 3 увеличится пропорционально первой степени K, но не второй.<br> | ||
| + | 3. Алгоритм требует в некоторые моменты времени производить синхронизацию и обмены данными по принципу «все со всеми». Это вызовет существенную эксплуатацию среды коммуникации, что приведёт к ухудшению | ||
| + | эффективности распараллеливания при большом числе процессоров.<br> | ||
| + | Обозначенные факты подтверждаются результатами запусков. | ||
| + | На первом графике видно, что при равномерном увеличении P и K время работы программы остаётся примерно неизменным на этапах 1 и 2 и линейно растёт на этапе 3. | ||
| + | Но, при P > 128 ситуация резко ухудшается и время работы начинает возрастать (при увеличении количества процессоров с 256 до 1024 время работы на первом этапе возросло в 6 раз, до этого почти не менялось). | ||
| + | Это объясняется возросшими накладными расходами на обеспечение межпроцессорного взаимодействия. | ||
| + | Второй график демонстрирует зависимость времени выполнения от количества процессоров. График характерен для сильной масштабируемости: при P < 256 время убывает по P как гипербола. | ||
| + | Этот же факт нашёл отражение в графике эффективности распараллеливания: при тех же P эффективность распараллеливания в целом не опускается ниже 0,65, в среднем держится на уровне 0,8. | ||
| + | Резкое падение эффективности реализации третьего шага в начале обусловлено появлением обмена данными при переходе от 1 процессора к двум. На долю третьего этапа выпадает существенная доля обмена данными. | ||
| + | При P > 256 эффективность начинает быстро убывать, но стабилизируется на уровне 0,15. Выигрыш по времени по прежнему есть, но уже не такой существенный. | ||
| + | При исследовании сильной масштабируемости параметр K был зафиксирован равным 1024. | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
== Выводы для классов архитектур == | == Выводы для классов архитектур == | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| + | Данный алгоритм основан на методе С. А. Ломова построения точных решений. Не известно о существовании его реализаций. | ||
| + | В целом, дифференциальные уравнения с вырождениями представляют весьма мало изученную область математики. | ||
= Литература = | = Литература = | ||
<references \> | <references \> | ||
Текущая версия на 01:24, 21 ноября 2017
| Алгоритм построения приближённого решения нерегулярно вырождающегося эллиптического дифференциального уравнения | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(KN\mathrm{max}(K, N))[/math] |
| Объём входных данных | [math]KN + 2N[/math] |
| Объём выходных данных | [math]KN[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(\mathrm{max}(K, N^2))[/math] |
| Ширина ярусно-параллельной формы | [math]O(KN)[/math] |
Автор описания: Д. П. Емельянов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм позволяет построить приближения к точному решению эллиптического дифференциального уравнения с нерегулярным вырождением и аналитическими коэффициентами в прямоугольнике. Точные формулы решения уравнения и их строгое обоснование получены с использованием метода спектрального выделения особенностей[1]. Решение строится в виде ряда. Погрешность алгоритма заключается в замене рядов на конечные суммы.
Алгоритм решает следующую задачу:
- [math] \begin{cases} y^2u''_{yy}+u''_{xx}+c(y)u'_y-a(y)u=f(x,y),(x,y)\in(0,1)\times(0,b), \\ u(0,y)=u(1,y)=u(x,b)=0,|u(x,0)|\lt +\infty. \end{cases}[/math]
Функции [math]a(y), c(y)[/math] полагаем аналитическими в круге [math]|y|\lt R[/math], где [math]R\gt b[/math]. Кроме того, [math]c(y), a(y) \ge 0[/math] в [math][0,b][/math], [math]c(0)=0[/math].
1.2 Математическое описание алгоритма
1. Приблизим функцию [math]f(x,y)[/math] конечными суммами ряда Фурье по [math]x[/math]:
- [math]f(x,y)=\sum_{k=1}^{K}f_k(y)\sin \pi kx.[/math]
- [math]f_k(y)=2\int\limits_0^1f(x,y)\sin \pi kx\,dx.[/math]
Для интеграла следует использовать квадратурную формулу.
2. Приблизим функции [math]f_k(y),a(y),c(y)[/math] полиномами:
- [math]a(y)=\sum_{n=0}^{N}a_ny^n, c(y)=\sum_{n=1}^{N}c_ny^n, f_k(y)=\sum_{n=0}^{N}f_{kn}y^n.[/math]
Разложение можно проводить по аналогии с разложением в ряд Фурье, но с использованием полиномов Лежандра, Чебышёва, или той же тригонометрической системы функций. Можно использовать интерполяционные полиномы.
3. Введём в рассмотрение числа:
- [math]\lambda_k=\pi^2k^2+a_0, k = \overline{1,K},[/math]
- [math]r_k=\frac{1-c_1 + \sqrt{(c_1-1)^2+4\lambda_k}}{2}, k = \overline{1,K}.[/math]
4. Построим функции [math]\eta_k(y),\varphi_k(y)[/math], они будут использованы при построении приближения к решению:
- [math]\eta_k(y)=\sum_{n=0}^{N}\eta_{kn}y^n, \stackrel{\circ}{\varphi}_k(y)=\sum_{n=0}^{N}\varphi_{kn}y^n,[/math]
- [math]\begin{matrix} \eta_{kn}=\frac{f_{kn}-\sum_{l=2}^{n+1}c_l(n+1-l)\eta_{k,n+1-l}+ \sum_{l=1}^{n}a_l\eta_{k,n-l}}{n(n-1)+nc_1-\pi^2k^2-a_0},n = \overline{1,N},\\ \varphi_{kn}=\frac{ \sum_{l=1}^na_l\varphi_{k,n-l}- \sum_{l=2}^{n+1}(n-l+1+r_k)c_l\varphi_{k,n-l+1} }{n(n-1)+2nr_k+nc_1} ,n= \overline{1,N},\\ \eta_{k,0}=\frac{f_{k,0}}{-\pi^2k^2-a_0}, \varphi_{k,0}=1, \varphi_k(y)=-\frac{\eta_k(b)}{\stackrel{\circ}{\varphi}_k(b)}\stackrel{\circ}{\varphi}_k(y). \end{matrix}[/math]
5. Построим приближение к решению:
- [math]u(x,y)=\sum_{k=1}^{K}\left(\left(\frac{y}{b}\right)^{r_k}\varphi_k(y)+\eta_k(y)\right)\sin \pi kx.[/math]
За счёт выбора [math]K[/math] и [math]N[/math] можно добиться той или иной точности.
1.3 Вычислительное ядро алгоритма
Алгоритм решения задачи можно разделить на три крупные части примерно одинаковой вычислительной сложности:
1. Разложение заданной функции [math]f(x,y)[/math] в ряд Фурье, разложение её коэффициентов Фурье в ряды Тейлора, разложение заданных функций [math]a(y), c(y)[/math] в ряды Тейлора.
На этом этапе известные сеточные функции скалярно умножаются на тригонометрические функции или полиномы Лежандра. В первом случае коэффициент является скалярным произведением,
во втором - линейной комбинацией соответствующих коэффициентов полиномов Лежандра, помноженных на отвечающие данному полиному скалярные произведения.
2. Построение коэффициентов ряда Тейлора для функций [math]\eta_k(y), \varphi_k(y)[/math] с последующим построением самих функций.
Используются формулы этапа 4 пункта 1.2.
3. По построенным функциям [math]\eta_k(y), \varphi_k(y)[/math] строится решение задачи [math]u(x,y)[/math] (формула этапа 5 пункта 1.2).
1.4 Макроструктура алгоритма
Макроструктура этого алгоритма фактически совпадает с его вычислительным ядром (см. пункт 1.3).
1.5 Схема реализации последовательного алгоритма
Алгоритм принимает на вход сеточные функции [math]f(x_i, y_j), a(y_j), c(y_j); x_i = \frac{i}{K}, y_j = \frac{j}{N}; i = \overline{0,K-1}, j=\overline{0,N-1}[/math].
- [math] f_k(y_j) = \frac{2}{K}\sum_{l=1}^K f(x_l, y_j) sin (\pi kx_l), k=\overline{1,K},\\ f_{kn} = \sum_{m=0}^{N-1} (\mathrm{coeff}_n L_m) \frac{2}{N} \sum_{l=0}^{N-1} f_k(y_l) L_m(y_l), n=\overline{0,N-1},\\ a_{n} = \sum_{m=0}^{N-1} (\mathrm{coeff}_n L_m) \frac{2}{N} \sum_{l=0}^{N-1} a(y_l) L_m(y_l),\\ c_{n} = \sum_{m=0}^{N-1} (\mathrm{coeff}_n L_m) \frac{2}{N} \sum_{l=0}^{N-1} c(y_l) L_m(y_l). [/math]
Тут [math]\mathrm{coeff}_n[/math] - коэффициент при n-й степени y в полиноме-аргументе (подразумевается, что алгоритм их знает), [math]L_m[/math] - нормированный полином Лежандра степени m.
Формулы для вычислений на других шагах алгоритма изложены в пункте 1.2. Достаточно заметить, что при все функции вычисляются в узлах заданной сетки, суммирование можно вести, запоминая [math]y^{n-1}[/math]
с предыдущего шага, вычисляется лишь [math]y^{n-1}y[/math].
1.6 Последовательная сложность алгоритма
Будем оценивать количество операций умножения вещественных чисел. Произведём оценку отдельно для каждого шага алгоритма.
1. [math](K + 1)KN[/math] умножение для вычисления всех [math]f_k(y_j)[/math] (N возникает в силу необходимости вычислять функцию в каждой точке сетки по y),
[math]((N + 1)N + 1)K[/math] операций для вычисления [math]f_{kn}[/math] (считаем, что значения гармоник и полиномов Лежандра известны заранее,
учитываем равенство некоторых скалярных произведений при вычислении),
[math]2((N + 1)N + 1)[/math] операций для вычисления [math]a_n, c_n[/math].
2. Для вычисления n-го коэффициента требуется [math]5 + 3(n-1)[/math] операций, для вычисления всех коэффициентов -
[math]\sum_{n=1}^{N-1} (5 + 3(n-1))=5(N-1) + 3\frac{N-2}{2}(N-1)=(N-1)(5 + 1,5 (N-2))[/math], суммирование [math]\stackrel{\circ}{\varphi}_k(b)[/math] требует [math]2N[/math] операций,
коррекция [math]\varphi_k(y_j)[/math] требует [math]N + 2[/math] операции, построение самих функций - [math]N(2N)=2N^2[/math] операций. Это всё нужно проделать [math]K[/math] раз.
3. Вычисление значения функции в узле сетки стоит [math]3K[/math] операций умножения. Это нужно проделать в [math]KN[/math] узлах.
Выделим главный член асимптотики по всем шагам: [math]K^2N + KN^2 + 3,5KN^2 + 3K^2N=O(KN\mathrm{max}(K,N)).[/math]
Если положить [math]K=N[/math], то сложность алгоритма имеет порядок [math]O(N^3)[/math].
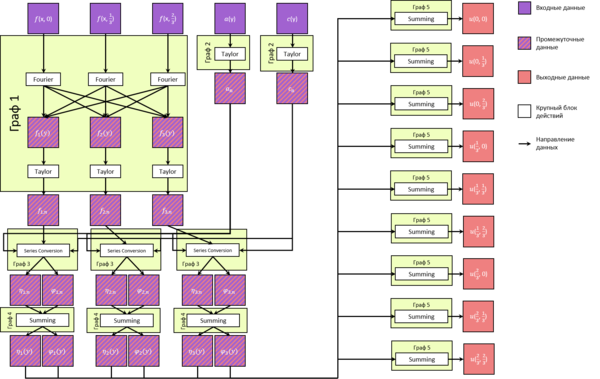
1.7 Информационный граф
Приведём информационные графы для каждой части алгоритма отдельно (иначе граф чрезмерно громоздкий).
1. Построение коэффициентов [math]f_{kn}[/math] по функции [math]f(x,y)[/math] (тут и далее K = N = 3).
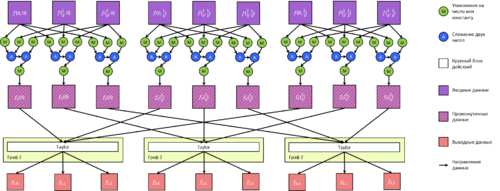
2. Построение коэффициентов [math]a_n, c_n[/math] осуществляется по общей схеме.
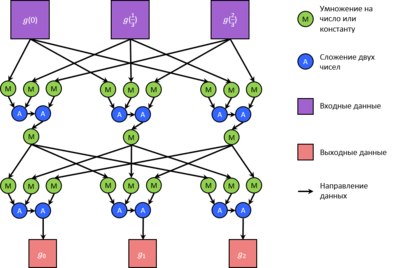
3. Построение коэффициентов [math]\eta_{kn}, \varphi_{kn}[/math] при фиксированном k.
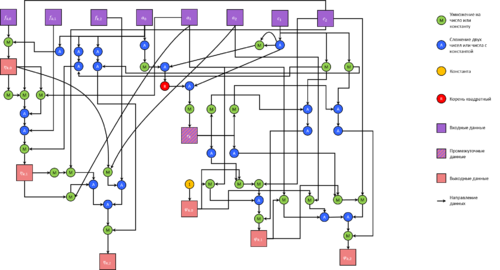
4. Построение самих функций [math]\eta_k(y), \varphi_k(y)[/math].
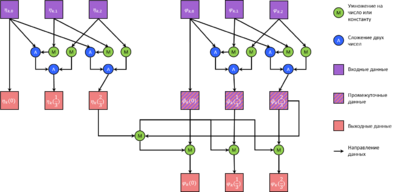
5. Построение решения в некоторой точке [math](x,y)[/math].
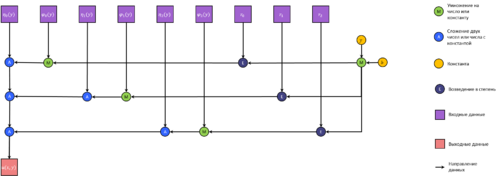
Макроструктуру всего алгоритма можно описать следующим графом:
1.8 Ресурс параллелизма алгоритма
Будем оценивать параллельную сложность алгоритма в терминах блоков из пункта 1.7.
Предполагаем для простоты, что любые данные, помеченные промежуточными на общем графе, доступны с любой параллельной ветви
(для обеспечения этого в программе потребуется синхронизация на промежуточных этапах с обменом информацией).
Длинные операции суммирования считаем выполняемыми последовательно (без параллелизма). На практике это имеет смысл в силу малой сложности суммы.
Распараллеливание только замедлит программу за счёт обмена данными.
Итак, в первом блоке операций каждый коэффициент Фурье в каждой точке может быть вычислен независимо от других. Числа [math]f_{kn}[/math] также вычисляются независимо при различных K и N.
В этом случае параллельная сложность - [math]O(\mathrm{max}(K,N))[/math].
Допустив суммирование сдваиванием, получим [math]O(\log_2 \mathrm{max}(K,N))[/math]. Параллелизм по K и N - массовый, в случае суммирования сдваиванием имеем дополнительно скошенный параллелизм.
Вычисление [math]a_n, c_n[/math] не зависит от [math]f_{kn}[/math], его можно выполнить параллельно (конечный параллелизм). Сами же вычисления за счёт массового параллелизма по N упрощаются
до параллельной сложности [math]O(N)[/math].
Третий блок, как видно из общего графа, допускает массовый параллелизм по K. Однако, внутренние вычисления, как видно из третьего графа, весьма запутанные и не допускают координатного параллелизма
(достаточно заметить в формулах, что каждый следующий n+1-й коэффициент требует знания всех предыдущих для вычисления). В этом случае параллельная сложность - [math]O(N^2)[/math].
С использованием скошенного параллелизма можно потенциально сократить параллельную сложность до [math]O(N)[/math], если все коэффициенты будут считаться параллельно.
Но в этом случае после вычисления каждого следующего коэффициента, необходимо передать его в параллельные ветви, вычисляющие другие (со старшими номерами).
Это на практике потребует существенных временных расходов на передачу данных и синхронизацию.
Вычисление же [math]\eta_k(y), \stackrel{\circ}{\varphi}_k(y)[/math] независимо в каждой точке y и при каждом индексе k. Массовый параллелизм. Параллельная сложность - [math]O(N)[/math].
Коррекция [math]\stackrel{\circ}{\varphi}_k(y)[/math] при этом имеет параллельную сложность [math]O(1)[/math].
И, наконец, вычисление решение можно вести независимо в каждой точке (массовый параллелизм). Параллельная сложность - [math]O(K)[/math], в случае суммирования сдваиванием - [math]O(\log_2 K)[/math].
Итоговая параллельная сложность алгоритма: [math]O(\mathrm{max}(K, N^2))[/math]. Использование суммирования сдваиванием и указанного подхода в третьем блоке позволяют уменьшить параллельную сложность до
[math]O(\mathrm{max}(\log_2 K, N))[/math].
1.9 Входные и выходные данные алгоритма
На вход алгоритм получает заданные на сетке функции [math]f(x,y), a(y), c(y)[/math] ([math](K+2)N[/math] вещественных чисел). На выходе у алгоритма заданное на сетке решение [math]u(x,y)[/math] ([math]KN[/math] вещественных чисел). Используется сетка, объявленная в пункте 1.5.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Будем рассматривать масштабируемость реализации алгоритма при некоторых ограничениях. Опираясь на пункт 1.8, заметим, что на шагах алгоритма 1 и 3 характер параллелизма по N имеет тот же характер, что и по K.
Кроме того, на шаге 2, как было замечено, без использования затратных в организации методов распараллеливания, параллельная сложность по N равна [math]O(N^2)[/math] и не может быть уменьшена.
Руководствуясь этими аргументами, положим во всех текстах [math]N=const=2048[/math] и исследуем ресурс параллелизма по K.
Все результаты запусков были получены на суперкомпьютере «Ломоносов»[2][3] (ссылка на технические характеристики в литературе).
Отметим следующие свойства, которые должны следовать из свойств алгоритма:
1. При P < K (P - количество процессоров) имеет место сильная масштабируемость. Действительно, не изменяя K, мы можем увеличить количество процессоров P (P < K).
В этом случае производительность должна пропорционально сократиться (см. пункт 1.8).
2. При P = K имеет место слабая масштабируемость, ибо при P > K не удастся равномерно загрузить все узлы работой и некоторые узлы будут бездействовать, однако,
в случае повышения K, вы вновь сможем увеличить количество процессоров так, что время работы программы на этапах 1 и 2 останется неизменным,
а на этапе 3 увеличится пропорционально первой степени K, но не второй.
3. Алгоритм требует в некоторые моменты времени производить синхронизацию и обмены данными по принципу «все со всеми». Это вызовет существенную эксплуатацию среды коммуникации, что приведёт к ухудшению
эффективности распараллеливания при большом числе процессоров.
Обозначенные факты подтверждаются результатами запусков.
На первом графике видно, что при равномерном увеличении P и K время работы программы остаётся примерно неизменным на этапах 1 и 2 и линейно растёт на этапе 3.
Но, при P > 128 ситуация резко ухудшается и время работы начинает возрастать (при увеличении количества процессоров с 256 до 1024 время работы на первом этапе возросло в 6 раз, до этого почти не менялось).
Это объясняется возросшими накладными расходами на обеспечение межпроцессорного взаимодействия.
Второй график демонстрирует зависимость времени выполнения от количества процессоров. График характерен для сильной масштабируемости: при P < 256 время убывает по P как гипербола.
Этот же факт нашёл отражение в графике эффективности распараллеливания: при тех же P эффективность распараллеливания в целом не опускается ниже 0,65, в среднем держится на уровне 0,8.
Резкое падение эффективности реализации третьего шага в начале обусловлено появлением обмена данными при переходе от 1 процессора к двум. На долю третьего этапа выпадает существенная доля обмена данными.
При P > 256 эффективность начинает быстро убывать, но стабилизируется на уровне 0,15. Выигрыш по времени по прежнему есть, но уже не такой существенный.
При исследовании сильной масштабируемости параметр K был зафиксирован равным 1024.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Данный алгоритм основан на методе С. А. Ломова построения точных решений. Не известно о существовании его реализаций. В целом, дифференциальные уравнения с вырождениями представляют весьма мало изученную область математики.
3 Литература
<references \>
- ↑ Ломов С. А., Ломов И. С. Основы математической теории пограничного слоя. М.: Издательство Московского университета, 2011. – 456 с.
- ↑ https://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%BC%D0%BE%D0%BD%D0%BE%D1%81%D0%BE%D0%B2_(%D1%81%D1%83%D0%BF%D0%B5%D1%80%D0%BA%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80)
- ↑ http://users.parallel.ru/wiki/pages/22-config
