Участник:Chist/Метод Ньютона: различия между версиями
Chist (обсуждение | вклад) |
Chist (обсуждение | вклад) |
||
| (не показано 13 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | Чистяков И.А., метод Ньютона | ||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
| Строка 6: | Строка 7: | ||
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства. | Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства. | ||
| − | Поскольку функция может иметь несколько корней, чтобы попытаться найти их все, необходимо провести перебор начальных приближений. При нас интересуют не только действительные корни, но и комплексные, будет производить перебор по некоторой сетке на комплексной плоскости. | + | Поскольку функция может иметь несколько корней, чтобы попытаться найти их все, необходимо провести перебор начальных приближений. При этом нас интересуют не только действительные корни, но и комплексные, будет производить перебор по некоторой сетке на комплексной плоскости. |
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| Строка 77: | Строка 78: | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| − | Последовательный алгоритм является частным случаем описанного алгоритма при <math>n = 1</math>. | + | Последовательный алгоритм является частным случаем описанного алгоритма при <math>n = 1</math>. При этом не возникает затрат на пересылку информации о найденных корнях к одному процессу, что позволяет более эффективно работать с памятью. |
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| Строка 100: | Строка 101: | ||
=== Информационный граф === | === Информационный граф === | ||
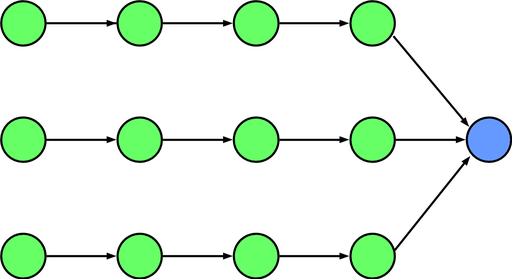
| − | + | Информационный граф алгоритма представлен на рисунке 1. Каждой зелёной вершине соответствует одна итерация алгоритма (при этом запущено <math>n</math> различных процессов), далее все полученные результаты пересылаются в один процесс для последующей обработки и вывода (синяя вершина). | |
| + | [[file:Newtone scheme.png|thumb|center|512px|Рисунок 1. Информационный граф алгоритма.]] | ||
| − | + | === Ресурс параллелизма алгоритма === | |
| − | + | Алгоритм является строго последовательным, однако существует возможность распараллеливания благодаря перебору. Таким образом сложность алгоритма равна <math>O(\frac{N \cdot M}{n})</math>. | |
| − | |||
| − | |||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| Строка 140: | Строка 140: | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| + | |||
| + | На рисунке 2 показана зависимость времени работы программы от количества процессоров и степени многочлена (рассматривались уравнения вида <math>z^p - 1 = 0</math>). | ||
| + | |||
| + | [[file:Newton_scale_results_3d.jpg|thumb|center|512px|Рисунок 2. Масштабируемость алгоритма.]] | ||
| + | |||
| + | Как видно из рисунка, время выполнения пропорционально степени полинома и обратно пропорционально числу процессоров, что согласуется с теоретическими результатами. На рисунке 3 показана зависимость времени работы от числа процессоров при фиксированной степени полинома <math>p = 4</math>. Можно заметить, что в данном случае полученные результаты достаточно хорошо аппроксимируются функцией <math>y(x) = 50 / x</math>. | ||
| + | |||
| + | [[file:Newton_scale_results.jpg|thumb|center|512px|Рисунок 3. Зависимость от числа процессоров.]] | ||
| + | |||
| + | |||
| + | Приведённые выше результаты были получены на суперкомпьютере “Ломоносов”. | ||
| + | Компиляция осуществлялась с помощью команды mpicc библиотеки OpenMPI, версия компилятора — gcc 1.8.4. При этом использовался ключ -std=c99, необходимый для использования описанной в языке Си реализации комплексных чисел. | ||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
| Строка 146: | Строка 158: | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| + | *Последовательные реализации | ||
| + | **ALIAS C++. Язык реализации — C++. Распространяется бесплатно, исходные коды и примеры использования можно скачать на сайте<ref name="ALIAS">https://www-sop.inria.fr/coprin/logiciels/ALIAS/ALIAS-C++/ALIAS-C++.html</ref>. | ||
| + | **Numerical Recipes. Язык реализации — C++. Исходный код можно найти в книге "Numerical recipes" <ref name="RECIPES">http://numerical.recipes</ref>. Бесплатно доступны<ref name="RECIPES_old">http://numerical.recipes/oldverswitcher.html</ref> предыдущие издания для языков C, Fortran77, Fortran90. | ||
| + | **Numerical Mathematics — NewtonLib. Язык реализации - C, Fortran. Исходные коды доступны<ref name="LIB_book">http://elib.zib.de/pub/elib/codelib/NewtonLib/index.html</ref> в качестве приложения к книге<ref name="LIB">https://www.amazon.com/Newton-Methods-Nonlinear-Problems-Computational/dp/364223898X/</ref> Peter Deuflhards "Newton Methods for Nonlinear Problems — Affine Invariance and Adaptive Algorithms". | ||
| + | |||
| + | *Параллельные реализации | ||
| + | **Sundials. Язык реализации — C, также есть интерфейс для использования в Fortran-программах. Распространяется<ref name="SUNDIALS_seq">http://computation.llnl.gov/projects/sundials/kinsol</ref> по лицензии BSD. | ||
| + | **PETSc. Язык реализации — C, есть интерфейс для Java и Python. Распространяется <ref name = PETSC>https://www.mcs.anl.gov/petsc/</ref> по лицензии BSD. | ||
== Литература == | == Литература == | ||
| − | |||
| − | |||
<references \> | <references \> | ||
Текущая версия на 11:01, 4 декабря 2017
Чистяков И.А., метод Ньютона
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
Поскольку функция может иметь несколько корней, чтобы попытаться найти их все, необходимо провести перебор начальных приближений. При этом нас интересуют не только действительные корни, но и комплексные, будет производить перебор по некоторой сетке на комплексной плоскости.
1.2 Математическое описание алгоритма
Пусть задана некоторая функция [math]\ f(x) [/math], её производная [math]\ f'(x) [/math] и сетка на комплексной плоскости вида
- [math] z_0 = \left( x_0 + \alpha \dfrac{x_1 - x_0}{N} \right) + i \cdot \left( y_0 + \beta \dfrac{y_1 - y_0}{M} \right), \qquad \alpha = \overline{1, N},\ \beta = \overline{1, M}, [/math]
где [math]\ i [/math] — мнимая единица.
Получим решения уравнения [math]\ f(z) = 0 [/math] с помощью итерационного процесса, определяемого формулой:
- [math] z_{k+1} = z_k - \dfrac{f(z_k)}{f'(z_k)}, [/math]
где в качестве начального приближения [math]\ z_0[/math] перебираются всевозможные точки рассмотренной сетки.
1.2.1 Теоретическое обоснование
Пусть [math]\ F(x)[/math] — оператор, отображающий линейное нормированное пространство [math]H[/math] на линейное нормированное пространство [math]Y[/math]. Линейный оператор [math]P[/math], действующий из пространства [math]H[/math] в пространство [math]Y[/math], назовём производной оператора [math]F(x)[/math] в точке [math]x[/math], если
- [math] \| F(x + \eta) − F(x) − P\eta \|_Y = o(\| \eta \|_H). [/math]
Будем обозначать такой оператор [math]P[/math] как [math]F′(x)[/math].
Пусть [math]\ X[/math] — решение уравнения [math]F(X) = 0[/math], [math]\ \Omega_a = \{ x: \| x - X \| \lt a \}[/math]. Пусть также при некоторых [math]a \gt 0,\ a_1 \ge 0,\ a_2 \le \infty[/math] выполнены условия:
- [math]\label{requirement_one} \| (F'(X))^{-1} \|_{Y} \le a_1 \text{ при } x \in \Omega_a, [/math]
- [math] \| F(u_1) - F(u_2) - F'(u_2)(u_1 - u_2) \|_{Y} \le a_2 \|u_2 - u_1 \|_{H}^{2} \text{ при } u_1, u_2 \in \Omega_a. [/math]
Обозначим [math]c = a_1 a_2[/math], [math]b = \min \{a, c^{-1}\}[/math].
Метод Ньютона применим на основании следующей теоремы:
Теорема. Если выполнены указанные условия и начальное приближение [math]x_0[/math] принадлежит [math]\Omega_b[/math], то итерационный процесс Ньютона
- [math] x_{n + 1} = x_{n} - (F'(x_n))^{-1} F(x_n) [/math]
сходится с оценкой погрешности
- [math] \| x_n - X \|_{H} \le c^{-1} \left( c \| x_0 - X \|_{H} \right)^{2^n}. [/math]
Доказательство этой теоремы можно найти в литературе[1].
1.3 Вычислительное ядро алгоритма
Вычислительную сложность алгоритма представляют операции вычисления значения функций в заданной точке, а так же операции вычитания и деления. При этом итерационный процесс запускается [math]N \cdot M[/math] раз, а количество итераций в каждом процессе, вообще говоря, не определено; наиболее популярными условиями останова являются следующие:
- [math] \| z_{n + 1} - z_{n} \| \lt \varepsilon, [/math]
- [math] | f(z_{n}) | \lt \varepsilon. [/math]
Однако, для верхней оценки числа операций удобно зафиксировать число итераций в каждом процессе. Это так же позволит завершить вычисления в случае, если итерационный процесс не сходится.
1.4 Макроструктура алгоритма
Для обеспечения параллелизма сперва исходная сетка разбивается на [math]n[/math] по возможности равных участков (например, на полосы длины [math]M[/math]) — запускается [math]n[/math] процессов. В каждом участке последовательно запускаются итерационные процессы для каждого узла сетки, в ходе которых:
- 1. вычисляются значения функций [math]\ f(z_k)[/math], [math]\ f'(z_k)[/math] (предполагается, что функции заданы аналитически);
- 2. вычисляется следующая точка:
- [math] z_{k+1} = z_k - \dfrac{f(z_k)}{f'(z_k)}; [/math]
- 3. если условие останова не выполнено, переходим к шагу 1.
Поскольку полученные в каждом процессе результаты необходимо обработать (проверить, являются ли полученные числа корнями; также желательно оставить только уникальные решения), нужно переслать полученные данные в какой-то один процесс. Проверку корней можно осуществлять на том процессоре, где они были получены, но это вызовет дополнительные сложности при работе с памятью во время последующей пересылки.
1.5 Схема реализации последовательного алгоритма
Последовательный алгоритм является частным случаем описанного алгоритма при [math]n = 1[/math]. При этом не возникает затрат на пересылку информации о найденных корнях к одному процессу, что позволяет более эффективно работать с памятью.
1.6 Последовательная сложность алгоритма
Для определения сложности алгоритма, необходимо выбрать класс функций, для которого будет написана программа (предполагается, что функции [math]\ f(x) [/math], [math]\ f'(x) [/math] заданы аналитически). Проведём исследование для многочленов степени [math]p[/math], каждый из которых определяется вектором из [math]p + 1[/math] коэффициентов. Пусть выбран критерий останова, при котором каждое использование метода Ньютона включает в себя [math]iter\_num[/math] операций.
Основную вычислительную сложность представляют собой операции умножения и деления комплексных чисел с плавающей точкой, будем считать их суммарное количество. Однако, необходимо помнить, что операции над комплексными числами требуют больше ресурсов, чем операции над действительными числами.
Для вычисления значения многочлена степени [math]p[/math] в точке с помощью тривиального алгоритма необходимо [math]\frac{p(p+1)}{2} + p[/math] операций умножения. Воспользовавшись схемой Горнера, можно сократить число умножений до [math]p[/math]:
- [math] P(x) = ( \ldots (a_p x + a_{p-1}) x + a_{p-2})x + \ldots + a_1)x + a_0. [/math]
В каждой итерации метода нужно вычислить не только значение многочлена в точке, но и значение его производной в этой точке. Это добавляет ещё [math]p - 1[/math] операцию. Наконец, в каждой итерации производится ровно одно деление.
Учитывая количество узлов сетки и заданное количество итераций, получим общее число операций умножения деления:
- [math] p + N \cdot M \cdot iter\_num \cdot (p + (p - 1) + 1) = p + 2 \cdot N \cdot M \cdot iter\_num \cdot p, [/math]
где первое слагаемое соответствует числу операций для вычисления коэффициентов производной многочлена.
1.7 Информационный граф
Информационный граф алгоритма представлен на рисунке 1. Каждой зелёной вершине соответствует одна итерация алгоритма (при этом запущено [math]n[/math] различных процессов), далее все полученные результаты пересылаются в один процесс для последующей обработки и вывода (синяя вершина).
1.8 Ресурс параллелизма алгоритма
Алгоритм является строго последовательным, однако существует возможность распараллеливания благодаря перебору. Таким образом сложность алгоритма равна [math]O(\frac{N \cdot M}{n})[/math].
1.9 Входные и выходные данные алгоритма
Входные данные:
- [math]p + 1[/math] действительное число — коэффициенты многочлена.
- Действительные числа [math]x_0[/math], [math]y_0[/math], [math]x_1[/math], [math]y_1[/math], определяющие левый нижний [math](x_0, y_0)[/math] и правый верхний [math](x_1, y_1)[/math] узлы прямоугольной сетки.
- Натуральные числа [math]M[/math] и [math]N[/math], задающие количество узлов сетки по горизонтали и вертикали
- Натуральное число [math]iter\_num[/math], равное количеству итераций при каждом запуске метода Ньютона
Выходные данные:
- список всех найденных комплексных чисел [math]z[/math], удовлетворяющих условию [math]|f(z)| \lt \varepsilon[/math].
1.10 Свойства алгоритма
Как хорошо видно, соотношение последовательной и параллельной сложности является линейным.
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, так же является линейной.
Очевидно, что алгоритм является детерминированным.
Как уже было замечено, могут возникнуть задержки в связи с пересылкой данных от каждого процесса к первому. Это связано не только с тем, что в первом процессе так же происходят вычисления, но и с тем, что несколько процессов могут отправить запросы на пересылку одновременно. В результате может возникнуть неоптимальное использование мощностей.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
Основная идея параллелизма заключается в разбиении сетки на [math]n[/math] участков. Идеи параллелизма можно также применять при вычислении значения многочлена в точке, однако это становится нерациональным при использовании схемы Горнера. Стоит отметить, что, за исключением перебора по сетке, в алгоритме нет каких-либо циклов.
2.4 Масштабируемость алгоритма и его реализации
На рисунке 2 показана зависимость времени работы программы от количества процессоров и степени многочлена (рассматривались уравнения вида [math]z^p - 1 = 0[/math]).
Как видно из рисунка, время выполнения пропорционально степени полинома и обратно пропорционально числу процессоров, что согласуется с теоретическими результатами. На рисунке 3 показана зависимость времени работы от числа процессоров при фиксированной степени полинома [math]p = 4[/math]. Можно заметить, что в данном случае полученные результаты достаточно хорошо аппроксимируются функцией [math]y(x) = 50 / x[/math].
Приведённые выше результаты были получены на суперкомпьютере “Ломоносов”.
Компиляция осуществлялась с помощью команды mpicc библиотеки OpenMPI, версия компилятора — gcc 1.8.4. При этом использовался ключ -std=c99, необходимый для использования описанной в языке Си реализации комплексных чисел.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- Последовательные реализации
- ALIAS C++. Язык реализации — C++. Распространяется бесплатно, исходные коды и примеры использования можно скачать на сайте[2].
- Numerical Recipes. Язык реализации — C++. Исходный код можно найти в книге "Numerical recipes" [3]. Бесплатно доступны[4] предыдущие издания для языков C, Fortran77, Fortran90.
- Numerical Mathematics — NewtonLib. Язык реализации - C, Fortran. Исходные коды доступны[5] в качестве приложения к книге[6] Peter Deuflhards "Newton Methods for Nonlinear Problems — Affine Invariance and Adaptive Algorithms".
- Параллельные реализации
3 Литература
<references \>
- ↑ Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков, Численные методы. Издательство «БИНОМ. Лаборатория знаний», 2008.
- ↑ https://www-sop.inria.fr/coprin/logiciels/ALIAS/ALIAS-C++/ALIAS-C++.html
- ↑ http://numerical.recipes
- ↑ http://numerical.recipes/oldverswitcher.html
- ↑ http://elib.zib.de/pub/elib/codelib/NewtonLib/index.html
- ↑ https://www.amazon.com/Newton-Methods-Nonlinear-Problems-Computational/dp/364223898X/
- ↑ http://computation.llnl.gov/projects/sundials/kinsol
- ↑ https://www.mcs.anl.gov/petsc/