Участник:NataliaPolienko/Блочное умножение матриц по методу Кеннона: различия между версиями
| (не показаны 22 промежуточные версии этого же участника) | |||
| Строка 57: | Строка 57: | ||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| − | + | Этап инициализации алгоритма Кеннона включает выполнение следующих операций передачи данных: | |
| − | + | ||
| − | + | Каждому процессору <math>p_{ij}</math> <math>(i = [1, m]</math>, <math>j = [1, m]</math>, где <math>m</math> - количество блоков<math>)</math> передаются блок <math>A_{i, \ j+i-1}</math> исходной матрицы <math>A</math> и блок <math>B_{i+j-1, \ j}</math> исходной матрицы <math>B</math>. Каждый процессор <math>p_{ij}</math> вычисляет свой блок матрицы <math>C</math> <math>(C_{ij})</math>. | |
| − | + | ||
| − | + | Операции на каждом последующем этапе: | |
| − | </math> | + | |
| + | 1. Вычисляется произведение блоков каждым процессором в соответствии с описанным ранее [[#Вычислительное ядро алгоритма| ядром алгоритма]] <math>(C_{ij} = C_{ij} + A_{ij}*B_{ij})</math>; | ||
| + | |||
| + | 2. Для каждой строки решетки блоки матрицы <math>A</math> циклически сдвигаются на координату <math>i, j-1</math>; | ||
| + | |||
| + | 3. Для каждого столбца решетки блоки матрицы <math>B</math> циклически сдвигаются на координату <math>i-1, j</math>; | ||
| + | |||
| + | После выполнения <math>m</math> итераций каждым процессором будет вычислен блок результирующей матрицы <math>C</math>. | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| Строка 84: | Строка 91: | ||
Опишем [[глоссарий#Граф алгоритма|граф алгоритма]]<ref>Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.</ref> как аналитически, так и в виде рисунка. | Опишем [[глоссарий#Граф алгоритма|граф алгоритма]]<ref>Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.</ref> как аналитически, так и в виде рисунка. | ||
| − | Граф алгоритма умножения квадратных матриц методом Кеннона состоит из одной группы вершин, расположенной в целочисленных узлах трёхмерной области, соответствующая ей операция вычисляет функцию | + | Граф алгоритма умножения квадратных матриц методом Кеннона состоит из одной группы вершин, расположенной в целочисленных узлах трёхмерной области, соответствующая ей операция вычисляет функцию <math>f = с+a*b</math>. |
Естественно введённые координаты области таковы: | Естественно введённые координаты области таковы: | ||
| Строка 107: | Строка 114: | ||
| − | [[file: | + | [[file:withoutin_cl.png|thumb|center|800px|Рисунок 1. Умножение квадратных матриц методом Кеннона]] |
| − | [[file: | + | [[file:drawing_cl.png|thumb|center|800px|Рисунок 2. Умножение квадратных матриц методом Кеннона с входными и выходными параметрами]] |
<br/> | <br/> | ||
| Строка 134: | Строка 141: | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| + | ====Масштабируемость алгоритма==== | ||
Проведём исследование масштабируемости параллельной реализации перемножения матриц методом Кеннона. Исследование проводилось на суперкомпьютере "Ломоносов"<ref name="Lom">Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.</ref> [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета]. | Проведём исследование масштабируемости параллельной реализации перемножения матриц методом Кеннона. Исследование проводилось на суперкомпьютере "Ломоносов"<ref name="Lom">Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.</ref> [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета]. | ||
| Строка 143: | Строка 151: | ||
В результате проведённых экспериментов был получен следующий диапазон [[Глоссарий#Эффективность реализации|эффективности реализации]] алгоритма: | В результате проведённых экспериментов был получен следующий диапазон [[Глоссарий#Эффективность реализации|эффективности реализации]] алгоритма: | ||
| − | * минимальная эффективность реализации 0. | + | * минимальная эффективность реализации 0.43%; |
| − | * максимальная эффективность реализации | + | * максимальная эффективность реализации 91.56%. |
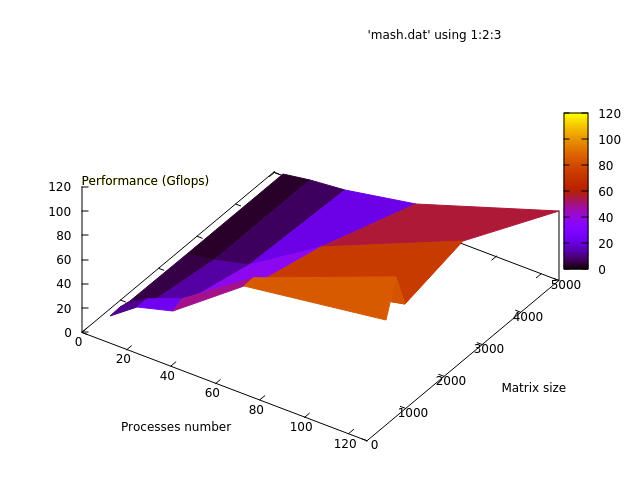
| − | Ниже приведены графики зависимости вычислительного времени алгоритма | + | Ниже приведены графики зависимости эффективности, вычислительного времени и производительности алгоритма от изменяемых параметров запуска — размера данных и числа процессоров: |
| − | [[file: | + | [[file:gr_sr.png|thumb|center|700px|Рисунок 3. Параллельная реализация перемножения матриц методом Кеннона. Изменение эффективности в зависимости от числа процессоров и размера матриц.]] |
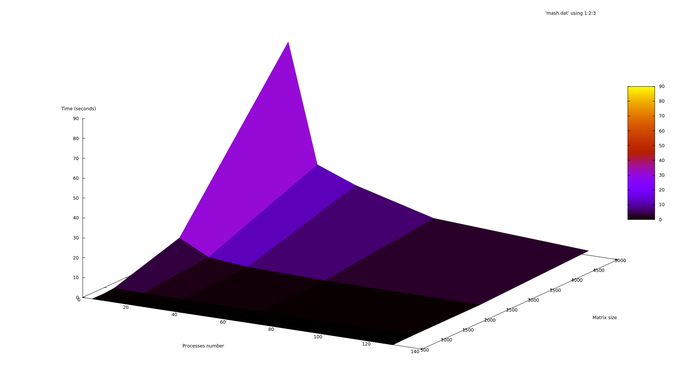
[[file:time_gr.png|thumb|center|700px|Рисунок 4. Параллельная реализация перемножения матриц методом Кеннона. Изменение времени, затраченного на счетную часть, в зависимости от числа процессоров и размера матриц.]] | [[file:time_gr.png|thumb|center|700px|Рисунок 4. Параллельная реализация перемножения матриц методом Кеннона. Изменение времени, затраченного на счетную часть, в зависимости от числа процессоров и размера матриц.]] | ||
| Строка 156: | Строка 164: | ||
Проведем оценки масштабируемости: | Проведем оценки масштабируемости: | ||
* По числу процессов: при увеличении числа процессов на всей рассмотренной области изменений параметров запуска эффективность убывает достаточно интенсивно. Уменьшение эффективности на рассмотренной области работы параллельной программы связано с увеличением числа пересылок, с ростом числа процессов и как следствие ростом накладных расходов на организацию вычислений. Присутствует область, на которой при увеличении числа процессов эффективность возрастает, но при дальнейшем росте продолжает снижаться. Это объясняется декомпозицей данных, при которой наступает момент, когда размер матрицы позволяет блокам укладываться в КЭШ-память. | * По числу процессов: при увеличении числа процессов на всей рассмотренной области изменений параметров запуска эффективность убывает достаточно интенсивно. Уменьшение эффективности на рассмотренной области работы параллельной программы связано с увеличением числа пересылок, с ростом числа процессов и как следствие ростом накладных расходов на организацию вычислений. Присутствует область, на которой при увеличении числа процессов эффективность возрастает, но при дальнейшем росте продолжает снижаться. Это объясняется декомпозицей данных, при которой наступает момент, когда размер матрицы позволяет блокам укладываться в КЭШ-память. | ||
| − | * По размеру задачи: при увеличении размера задачи эффективность | + | * По размеру задачи: при увеличении размера задачи эффективность увеличивается по рассматриваемой области. Рост эффективности следует из того, что, чем больше объем данных, тем меньше времени тратится на ввод-вывод и обмены данными, а больше на счетную часть алгоритма. |
| − | * | + | Алгоритм хорошо масштабируем. |
| + | ====Сведения о программно-аппаратной среде==== | ||
| + | * Суперкомпьютер "Ломоносов"; | ||
| + | * Компиляция: MPI: impi/5.0.1-ofa (gcc/4.4.7) | ||
| + | Вычисления были проведены в очереди test. Ограничений на лимит времени на узел наложено не было. | ||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
Текущая версия на 22:53, 2 декабря 2017
Автор: Полиенко Н.А.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Одной из основных операций над матрицами является их перемножение. Данная операция широко применяется в большом количестве разных методов. Здесь мы рассмотрим умножение [math]C = AB[/math] квадратных матриц с помощью алгоритма Кеннона. Его суть заключается в том, что матрицы разбиваются на блоки, представляющие собой подматрицы исходных матриц. В следствии чего в качестве базовой подзадачи можно выбрать вычисления, связанные с определением одного из блоков результирующей матрицы [math]C[/math] [1].
1.2 Математическое описание алгоритма
Исходные данные: матрица [math]A[/math] размера [math]n \times n[/math], матрица [math]B[/math] размера [math]n \times n[/math].
Вычисляемые данные: матрица [math]C[/math] размера [math]n \times n[/math].
Исходные и результирующая матрицы представляются в виде наборов блоков. Операцию матричного умножения матриц [math]A[/math] и [math]B[/math] в блочном виде можно представить следующим образом [2]: [math] \begin{bmatrix} A_{11} & A_{12} & \cdots & A_{1k} \\ A_{21} & A_{22} & \cdots & A_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ A_{k1} & A_{k2} & \cdots & A_{kk} \end{bmatrix} \begin{bmatrix} B_{11} & B_{12} & \cdots & B_{1k} \\ B_{21} & B_{22} & \cdots & B_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ B_{k1} & B_{k2} & \cdots & B_{kk} \end{bmatrix} = \begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1k} \\ C_{21} & C_{22} & \cdots & C_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ C_{k1} & C_{k2} & \cdots & C_{kk} \end{bmatrix}, [/math]
где каждый блок [math]C_{ij}[/math] матрицы [math]C[/math] определяется в соответствии с выражением:
- [math] \begin{align} C_{ij} = \sum_{l = 1}^{k} A_{il} B_{lj}, \quad i \in [1, k], \quad j \in [1, k]. \end{align} [/math]
Полученные блоки [math]C_{ij}[/math] являются независимыми.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро перемножения матриц(квадратных) методом Кеннона можно составить из множественных вычислений умножения блоков матрицы [math]A[/math] на блоки матрицы [math]B[/math], таким образом получая блок результирующей матрицы [math]C[/math]:
- [math] \begin{align} C_{ij} = \sum_{l = 1}^{k} A_{il} B_{lj}, \quad i \in [1, k], \quad j \in [1, k]. \end{align} [/math]
1.4 Макроструктура алгоритма
Этап инициализации алгоритма Кеннона включает выполнение следующих операций передачи данных:
Каждому процессору [math]p_{ij}[/math] [math](i = [1, m][/math], [math]j = [1, m][/math], где [math]m[/math] - количество блоков[math])[/math] передаются блок [math]A_{i, \ j+i-1}[/math] исходной матрицы [math]A[/math] и блок [math]B_{i+j-1, \ j}[/math] исходной матрицы [math]B[/math]. Каждый процессор [math]p_{ij}[/math] вычисляет свой блок матрицы [math]C[/math] [math](C_{ij})[/math].
Операции на каждом последующем этапе:
1. Вычисляется произведение блоков каждым процессором в соответствии с описанным ранее ядром алгоритма [math](C_{ij} = C_{ij} + A_{ij}*B_{ij})[/math];
2. Для каждой строки решетки блоки матрицы [math]A[/math] циклически сдвигаются на координату [math]i, j-1[/math];
3. Для каждого столбца решетки блоки матрицы [math]B[/math] циклически сдвигаются на координату [math]i-1, j[/math];
После выполнения [math]m[/math] итераций каждым процессором будет вычислен блок результирующей матрицы [math]C[/math].
1.5 Схема реализации последовательного алгоритма
Алгоритм осуществляет последовательное вычисление блоков результирующей матрицы [math]C[/math]:
1. Матрицы [math]A[/math], [math]B[/math] разбиваются на блоки фиксированного размера(будем предполагать, что блоки квадратные и порядок матрицы делится на размер блока без остатка).
2. На одной итерации цикла по переменной [math]i[/math] используется первая строка, состоящая из блоков матрицы [math]A[/math] и все столбцы, состоящие из блоков матрицы [math]B[/math]:
[math] \begin{align} C_{ij} = \sum_{l = 1}^{k} A_{il} B_{lj}, \quad i \in [1, k], \quad j \in [1, k]. \end{align} [/math]
1.6 Последовательная сложность алгоритма
Для перемножения матриц размера [math]n \times n[/math] в последовательной реализации алгоритма требуется [math]n^3[/math] умножений и сложений.
1.7 Информационный граф
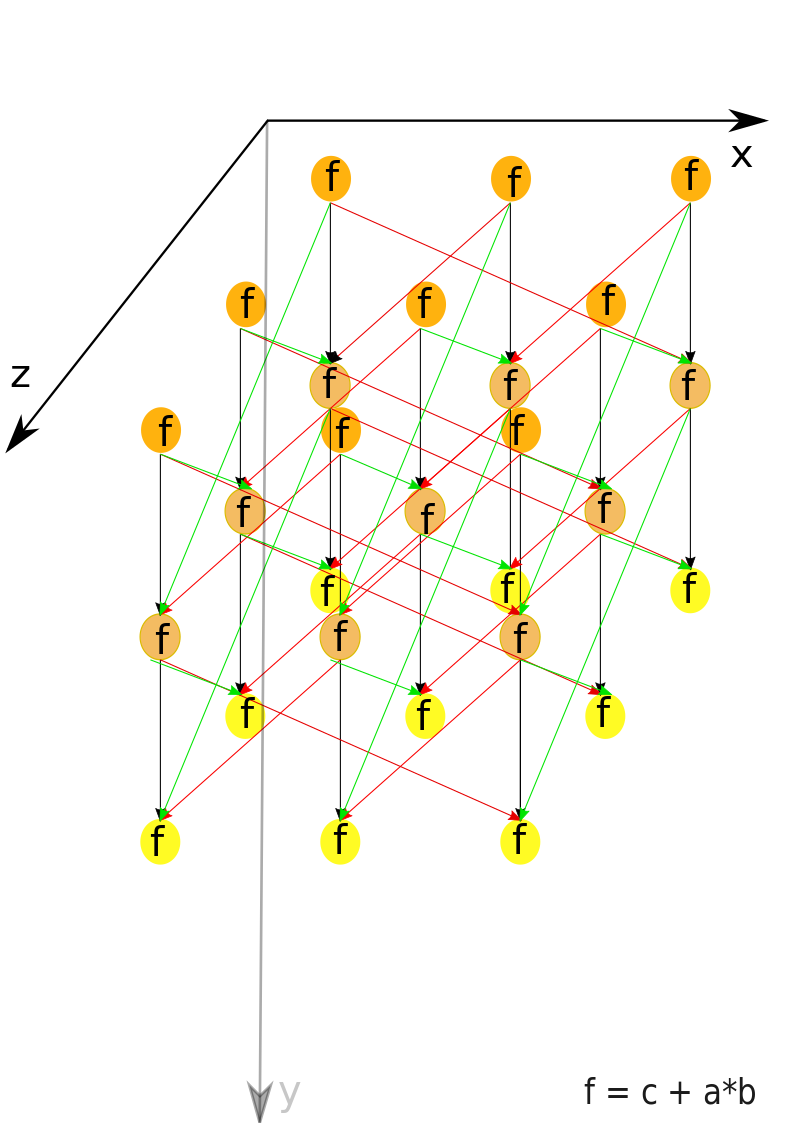
Опишем граф алгоритма[3] как аналитически, так и в виде рисунка.
Граф алгоритма умножения квадратных матриц методом Кеннона состоит из одной группы вершин, расположенной в целочисленных узлах трёхмерной области, соответствующая ей операция вычисляет функцию [math]f = с+a*b[/math].
Естественно введённые координаты области таковы:
- [math]i[/math] — меняется в диапазоне от [math]1[/math] до [math]m[/math], принимая все целочисленные значения;
- [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math]m[/math], принимая все целочисленные значения;
- [math]k[/math] — меняется в диапазоне от [math]1[/math] до [math]m[/math], принимая все целочисленные значения.
Аргументы операции следующие:
- [math]k = 1[/math]:
- [math]c = 0[/math];
- [math]a[/math]: элемент входных данных, а именно блок матрицы [math]A[/math] с координатами [math]i, j[/math];
- [math]b[/math] - элемент входных данных, а именно блок матрицы [math]B[/math] с координатами [math]i, j[/math];
- [math]k \gt 1[/math]:
- [math]c[/math] - результат срабатывания операции, соответствующей вершине с координатами [math]i, j, k-1[/math];
- [math]a[/math]: элемент, переданный из вершины [math]i, j+1, k-1[/math], являющийся элементом(блоком) матрицы [math]A[/math];
- [math]b[/math]: элемент, переданный из вершины [math]i+1, j, k-1[/math], являющийся элементом(блоком) матрицы [math]B[/math];
При [math]k \lt m[/math] - результатом выполнения операции является промежуточные данные алгоритма; При [math]k = m[/math] - выходными данными алгоритма([math]C_{ij}[/math]) будут являться результаты выполнения операции в узлах.
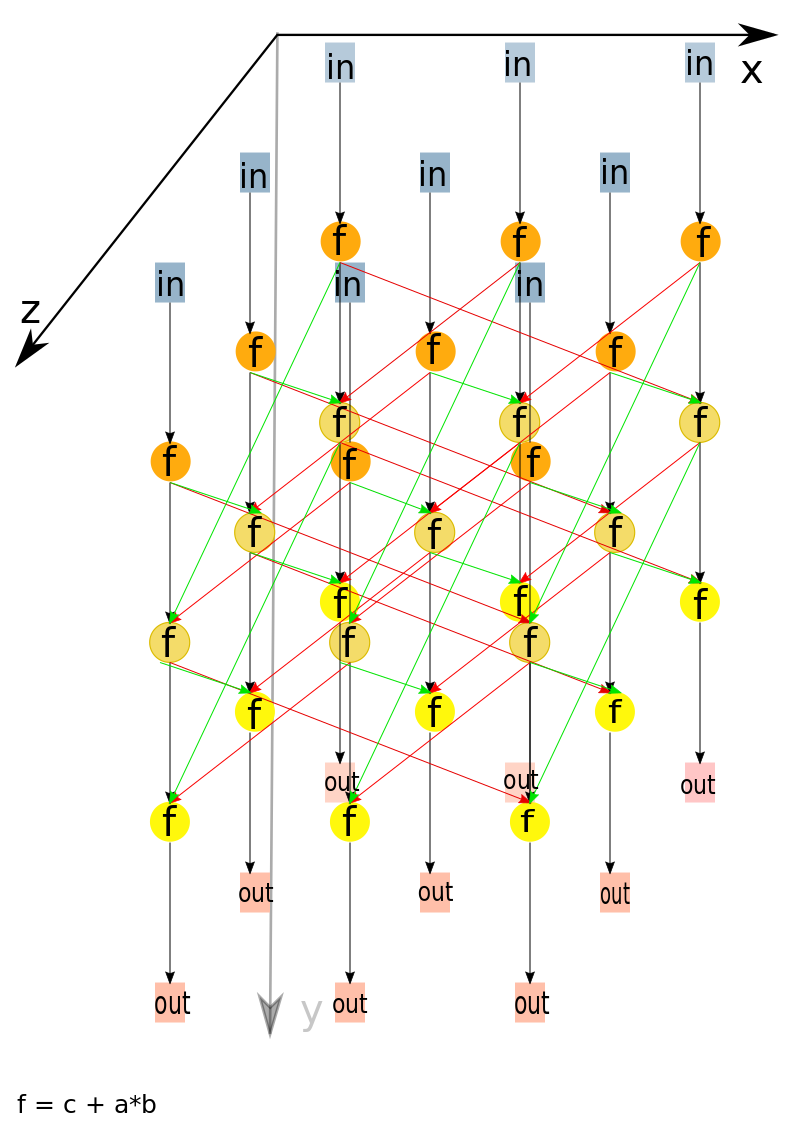
Описанный граф можно посмотреть на рис.1 и рис.2, выполненных для случая [math]m = 3[/math]([math]m [/math] - количество блоков, на которые разбиты исходные матрицы [math]A[/math] и [math]B[/math] ).Здесь красными стрелками указана циклическая передача данных, соответствующих блоку матрицы [math]A[/math], а зелеными стрелками - матрицы [math]B[/math]. На рис.1 показан граф алгоритма согласно классическому определению , на рис.2 к графу алгоритма добавлены вершины , соответствующие входным (обозначены синим цветом) и выходным (обозначены розовым цветом) данным.
1.8 Ресурс параллелизма алгоритма
Для алгоритма умножения квадратных матриц методом Кеннона размера [math]n \times n[/math] в параллельном варианте требуется последовательно выполнить следующие ярусы:
- по [math]m[/math] ярусов умножений и сложений (в каждом из ярусов — трудоемкость операции блочного умножения : [math](n/m)^2 \times (2n/m - 1)[/math], где [math]n/m[/math] - количество элементов в блоке, m - количество блоков).
Для сложения блоков требуется [math](n/m)^2[/math] операций.
1.9 Входные и выходные данные алгоритма
Входные данные: матрица [math]A[/math], матрица [math]B[/math].
Объём входных данных: [math]n \times n + n \times n[/math]
Выходные данные: матрица [math]C[/math] .
Объём выходных данных: [math]n \times n[/math]
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
Проведём исследование масштабируемости параллельной реализации перемножения матриц методом Кеннона. Исследование проводилось на суперкомпьютере "Ломоносов"[4] Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [4:128];
- размер матрицы [500:5000].
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 0.43%;
- максимальная эффективность реализации 91.56%.
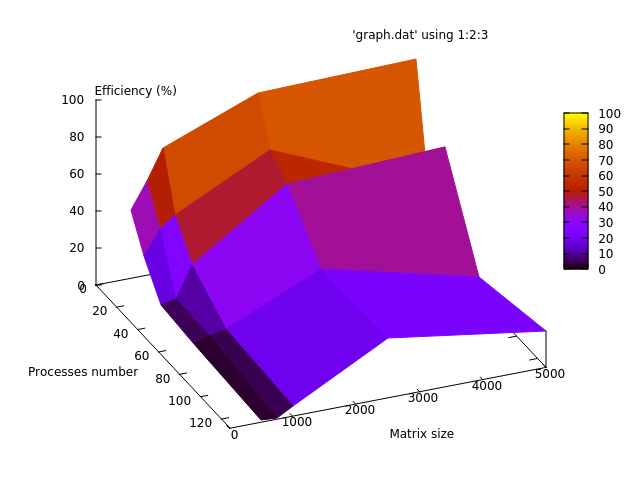
Ниже приведены графики зависимости эффективности, вычислительного времени и производительности алгоритма от изменяемых параметров запуска — размера данных и числа процессоров:
Проведем оценки масштабируемости:
- По числу процессов: при увеличении числа процессов на всей рассмотренной области изменений параметров запуска эффективность убывает достаточно интенсивно. Уменьшение эффективности на рассмотренной области работы параллельной программы связано с увеличением числа пересылок, с ростом числа процессов и как следствие ростом накладных расходов на организацию вычислений. Присутствует область, на которой при увеличении числа процессов эффективность возрастает, но при дальнейшем росте продолжает снижаться. Это объясняется декомпозицей данных, при которой наступает момент, когда размер матрицы позволяет блокам укладываться в КЭШ-память.
- По размеру задачи: при увеличении размера задачи эффективность увеличивается по рассматриваемой области. Рост эффективности следует из того, что, чем больше объем данных, тем меньше времени тратится на ввод-вывод и обмены данными, а больше на счетную часть алгоритма.
Алгоритм хорошо масштабируем.
2.4.2 Сведения о программно-аппаратной среде
- Суперкомпьютер "Ломоносов";
- Компиляция: MPI: impi/5.0.1-ofa (gcc/4.4.7)
Вычисления были проведены в очереди test. Ограничений на лимит времени на узел наложено не было.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- [1] - Центр суперкомпьютерных технологий
- [2] - некоторые подходы к эффективной реализации блочных матричных алгоритмов
- [3] - github
3 Литература
- ↑ http://www.math.tsu.ru/sites/default/files/mmf2/e-resources/Introduction_to_Parallel_Computations_L4(6).pdf
- ↑ http://www.intuit.ru/studies/courses/1156/190/lecture/4964?page=7
- ↑ Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.