Метод встречи посередине: различия между версиями
| [непроверенная версия] | [досмотренная версия] |
Konshin (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 6 промежуточных версий 2 участников) | |||
| Строка 14: | Строка 14: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Метод "Встреча посередине" криптоанализа блочных шифров был впервые предложен в 1977 году Уитфилдом Диффи и Мартином Хеллманом <ref> | + | Криптоанализом назвают науку восстановления (дешифрования) открытого (нешифрованного) текста без доступа к ключу. Попытка криптоанализа называется "атакой". |
| + | |||
| + | Метод "Встреча посередине" криптоанализа блочных шифров был впервые предложен в 1977 году Уитфилдом Диффи и Мартином Хеллманом <ref>Diffie Whitfield, Hellman Martin E. ''Exhaustive Cryptanalysis of the NBS Data Encryption Standard.'' - Journal Computer vol.10 pp.74–84 - June 1977</ref>. Встреча посередине используется для ускорения перебора ключей шифра за счёт увеличения требуемой памяти. Метод применим в случае каскадного построения сложного шифра из нескольких простых, другими словами, в случае последовательного применения шифрующих преобразований на разных ключах к блокам открытого текста. | ||
В качестве примера шифра, поддающегося атаке "встреча посередине" можно привести криптоалгоритм 2DES, являющийся модификацией шифра DES. В 2DES открытый текст шифруется дважды алгоритмом DES на двух разных 56-битных ключах. Однако из-за атаки "встреча посередине" сложность перебора двойного ключа (112 бит) шифра 2DES составляет <math>2^{57}</math> вместо ожидаемых <math>2^{112}</math>. | В качестве примера шифра, поддающегося атаке "встреча посередине" можно привести криптоалгоритм 2DES, являющийся модификацией шифра DES. В 2DES открытый текст шифруется дважды алгоритмом DES на двух разных 56-битных ключах. Однако из-за атаки "встреча посередине" сложность перебора двойного ключа (112 бит) шифра 2DES составляет <math>2^{57}</math> вместо ожидаемых <math>2^{112}</math>. | ||
| Строка 94: | Строка 96: | ||
3. C генерацией одной (достаточно большой) хэш-таблицы — <math>O(|K_1|) + O(|K_2|)=O(|K_1|+|K_2|)</math> | 3. C генерацией одной (достаточно большой) хэш-таблицы — <math>O(|K_1|) + O(|K_2|)=O(|K_1|+|K_2|)</math> | ||
| − | Пусть n - количество всевозможных пар <math>k_1,k_2</math> и пусть <math>|K_1|=|K_2|</math>. В этом случае <math>|K_1|=|K_2|=\sqrt n</math>. | + | Пусть <math>n</math> - количество всевозможных пар <math>k_1,k_2</math> и пусть <math>|K_1|=|K_2|</math>. В этом случае <math>|K_1|=|K_2|=\sqrt n</math>. |
Тогда сложность алгоритма в первых двух пунктах составляет <math>O(\sqrt n\log(n))</math>, в третьем — <math>O(\sqrt n)</math>. | Тогда сложность алгоритма в первых двух пунктах составляет <math>O(\sqrt n\log(n))</math>, в третьем — <math>O(\sqrt n)</math>. | ||
| Строка 132: | Строка 134: | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | |||
| − | |||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| − | === | + | === Результаты прогонов === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | == | + | == Литература == |
| − | + | <references /> | |
| − | + | [[Категория:Статьи в работе]] | |
| − | + | [[en:Meet-in-the-middle attack]] | |
Текущая версия на 16:24, 21 июля 2022
Автор описания (разделы 1, 2.4, 2.7): А.В.Батарина
| Метод встречи посередине | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(\sqrt n\log(n))[/math] |
| Объём входных данных | [math]O(\log(n))[/math] |
| Объём выходных данных | [math]\log(n)[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(1)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n)[/math] |
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Криптоанализом назвают науку восстановления (дешифрования) открытого (нешифрованного) текста без доступа к ключу. Попытка криптоанализа называется "атакой".
Метод "Встреча посередине" криптоанализа блочных шифров был впервые предложен в 1977 году Уитфилдом Диффи и Мартином Хеллманом [1]. Встреча посередине используется для ускорения перебора ключей шифра за счёт увеличения требуемой памяти. Метод применим в случае каскадного построения сложного шифра из нескольких простых, другими словами, в случае последовательного применения шифрующих преобразований на разных ключах к блокам открытого текста.
В качестве примера шифра, поддающегося атаке "встреча посередине" можно привести криптоалгоритм 2DES, являющийся модификацией шифра DES. В 2DES открытый текст шифруется дважды алгоритмом DES на двух разных 56-битных ключах. Однако из-за атаки "встреча посередине" сложность перебора двойного ключа (112 бит) шифра 2DES составляет [math]2^{57}[/math] вместо ожидаемых [math]2^{112}[/math].
1.2 Математическое описание алгоритма
Исходные данные: открытый текст [math]x[/math], шифртекст [math]y[/math].
Алгоритм зашифрования — композиция двух преобразований: [math]T_1(x,k_1)[/math] и [math]T_2(x,k_2)[/math], т.е. [math]y=T_2(T_1(x,k_1),k_2)[/math].
Алгоритм расшифрования: [math]y=T_1^{-1}(T_2^{-1}(x,k_2),k_1)[/math].
Вычисляемые данные: ключи шифрования [math]k_1 \in K_1[/math], [math]k_2 \in K_2[/math], где [math]K_1, K_2[/math] — множества возможных ключей.
Трудоёмкость полного перебора всех возможных пар [math]k_1,k_2[/math] составляет в среднем [math]|K_1||K_2|/2[/math], а в худшем случае [math]|K_1||K_2|[/math]. Однако используя дополнительную память, можно сократить перебор.
Предположим, что открытый текст [math]x[/math] и шифртекст [math]y[/math] однозначно определяют ключи [math]k_1,k_2[/math]. Составим две таблицы:
[math] \begin{align} z_1 & =T_1(x,k_1^1) & z_1^′ &=T_2^{-1}(x,k_2^1)\\ z_2 & =T_1(x,k_1^2) & z_2^′ & =T_2^{-1}(x,k_2^2)\\ & ......... & & ......... \\ z_{|K_1|} & =T_1(x,k_1^{|K_1|}) & z_{|K_1|}^′ & =T_2^{-1}(x,k_2^{|K_1|}) \end{align} [/math]
Для всех [math]k_1^i \in K_1[/math], [math]k_2^j \in K_2[/math]. Далее таблицы объединяются и сортируются по значениям [math]z_i,z_j^′[/math]. Индексы [math]i,j[/math], при которых [math]z_i=z_j^′[/math], однозначно определяют искомую пару ключей [math]k_1=k_1^i,k_2=k_2^j[/math]. Для нахождения такой пары достаточно просмотреть отсортированную таблицу один раз.
Если же пара открытый текст/шифртекст определяет ключ не единственном образом, то выходом алгоритма будет некоторое множество пар [math]k_1,k_2[/math], одна из которых является истинным ключом. Для выбора истинного ключа достаточно проверить ключи из полученного множества на других парах открытый текст/шифртекст.
1.2.1 Оптимизации
1. От генерации второй таблицы со значениями [math]z_j^′[/math] можно отказаться, перебирая ключи [math]k_2^j[/math] до того момента, когда значение [math]z_j^′[/math] совпадёт с одним из значений [math]z_i[/math]. В таком случае опробование ключей [math]k_2^j[/math] в среднем сократится вдвое. Также вдвое сократится объём используемой памяти. Для нахождения совпадающего значения в отсортированном массиве можно применить бинарный поиск.
2. Вместо сортировки таблицы со значениями [math]z_i[/math] и последующего бинарного поиска можно использовать хэш-таблицу.
1.3 Вычислительное ядро алгоритма
В случае использования хэш-таблицы достаточно большого размера основную сложность алгоритма составляет опробование ключей [math]k_1,k_2[/math]. Одним из самых трудоёмких шагов также оказывается сортировка таблицы.
1.4 Макроструктура алгоритма
Как видно из описания, атака "встреча посередине" использует (или может использовать в качестве оптимизации) следующие алгоритмы:
1. Алгоритм зашифрования/расшифрования
2. Алгоритм сортировки
3. Алгоритмы поиска, вставки в хэш-таблицу
1.5 Схема реализации последовательного алгоритма
Далее приводится последовательность действий для варианта алгоритма с генерацией одной таблицы значений [math]z_i[/math].
1. Вычислить таблицу [math]z_i[/math], записывая значения в порядке вычисления или используя хэш-таблицу
2. В случае записи значений в порядке вычисления отсортировать массив
3. Опробовать ключи [math]k_2^j[/math], выполняя поиск совпадения с таблицей значений [math]z_j^′[/math]. Для нахождения совпадения использовать поиск по хэш-таблице (если она есть) или бинарный поиск
1.6 Последовательная сложность алгоритма
Всюду далее считаем, что алгоритм не прекращает работу при нахождении первого совпадения, а ищет все совпадения.
1. Сложность вычисления таблиц значений [math]z_i,z_j^′[/math] составит [math]O(|K_1|+|K_2|)[/math] операций опробования
2. Объединение таблиц и их сортировка будет иметь сложность [math]O((|K_1|+|K_2|)\log(|K_1|+|K_2|))[/math] (например, при сортировке слиянием).
3. Сложность бинарного поиска в отсортированном массиве — [math]O(\log_2(|K_1|))[/math] для каждого поиска
4. Сложность поиска в достаточно большой хэш-таблице составит [math]O(1)[/math] для каждого поиска
Итого: асимптотическая сложность алгоритма:
1. С генерацией двух таблиц — [math]O(|K_1|+|K_2|) + O((|K_1|+|K_2|)\log(|K_1|+|K_2|)) + O(|K_1|+|K_2|)=O((|K_1|+|K_2|)\log(|K_1|+|K_2|))[/math]
2. C генерацией одной таблицы, сортировкой и бинарным поиском — [math]O(|K_1|) + O((|K_1|)\log(|K_1|)) + O(|K_2|\log_2(|K_1|))=O(\max(|K_1|,|K_2|)\log(|K_1|))[/math]
3. C генерацией одной (достаточно большой) хэш-таблицы — [math]O(|K_1|) + O(|K_2|)=O(|K_1|+|K_2|)[/math]
Пусть [math]n[/math] - количество всевозможных пар [math]k_1,k_2[/math] и пусть [math]|K_1|=|K_2|[/math]. В этом случае [math]|K_1|=|K_2|=\sqrt n[/math].
Тогда сложность алгоритма в первых двух пунктах составляет [math]O(\sqrt n\log(n))[/math], в третьем — [math]O(\sqrt n)[/math].
1.7 Информационный граф
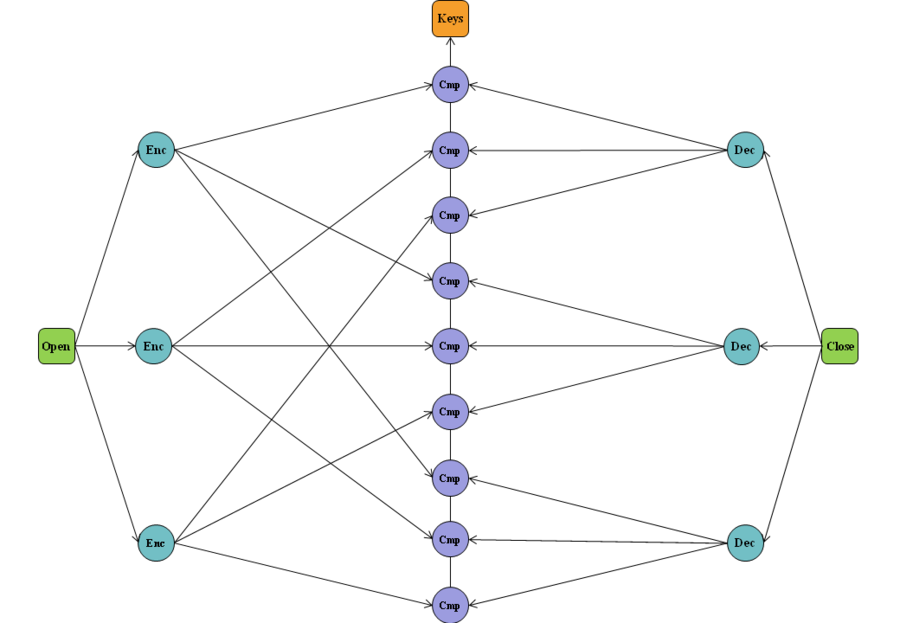
Опишем информационный граф алгоритма. На вход подаётся открытый (Open) и закрытый (Close), т.е. зашифрованный, текст. Далее открытый текст шифруется (Enc) на ключах [math]k_1^i[/math], а зашифрованный расшифровывается (Dec) на ключах [math]k_2^j[/math]. Далее полученные криптограммы сравниваются (Cmp) и все ключи, на которых они совпали, являются выходом алгоритма.
1.8 Ресурс параллелизма алгоритма
Как видно из информационного графа, для реализации атаки "встреча посередине" в параллельном варианте потребуются выполнение следующих двух ярусов (в предположении, что [math]|K_1|=|K_2|[/math]):
1. [math]\sqrt n[/math] зашифрований и столько же расшифрований
2. [math]n[/math] сравнений
Таким образом, высота ЯПФ составляет 2, ширина - [math]n[/math].
1.9 Входные и выходные данные алгоритма
Вход: На вход подаётся открытый текст [math]x[/math] и шифртекст [math]y[/math], а также алгоритм зашифрования/расшифрования. В случае блочного шифра открытым текстом и шифртекстом является последовательность блоков. Для атаки "встреча посередине", как правило, берётся один блок для максимального ускорения операций зашифрования и расшифрования.
Выход: Результатом работы алгоритма является множество пар [math]k_1^i,k_2^j[/math], для которых нашлись совпадения. Только одна из пар является настоящим ключом. Чтобы отсеять лишние, необходимо проверить все пары на блоках открытого и шифрованного текста, которые в алгоритме не использовались.
1.10 Свойства алгоритма
Соотношением последовательной и параллельной сложности алгоритма является [math]O(\sqrt n\log(n))[/math].
Будем считать, что размер входных данных (открытый текст и шифртекст) совпадает с размером ключа (на практике это сравнимые величины), а сортировка слиянием делит массивы пополам. Тогда вычислительная мощность алгоритма — [math]O(\sqrt n)[/math].
Дуги информационного графа, исходящие из вершин зашифрования и расшифрования, образуют пучки мощности [math]\sqrt n[/math], т.е. из каждой такой вершины выходит [math]\sqrt n[/math] дуг. Длинных дуг в алгоритме нет. В случае поиска всех пар ключей с совпадающими криптограммами алгоритм полностью детерминирован.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Возможные способы и особенности параллельной реализации алгоритма
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
3 Литература
- ↑ Diffie Whitfield, Hellman Martin E. Exhaustive Cryptanalysis of the NBS Data Encryption Standard. - Journal Computer vol.10 pp.74–84 - June 1977