Поиск в ширину (BFS): различия между версиями
| [выверенная версия] | [досмотренная версия] |
Apaokin (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 166: | Строка 166: | ||
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | |||
| − | |||
| − | |||
| − | |||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| − | === | + | === Результаты прогонов === |
| − | |||
| − | |||
| − | |||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Литература == | == Литература == | ||
Текущая версия на 10:59, 1 июля 2022
| Алгоритм поиска в ширину (BFS) | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(|V| + |E|)[/math] |
| Объём входных данных | [math]O(|V| + |E|)[/math] |
| Объём выходных данных | [math]O(|V|)[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]N/A, \max O(|V|) [/math] |
| Ширина ярусно-параллельной формы | [math]N/A, \max O(|E|) [/math] |
Основные авторы описания: И.В.Афанасьев
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Поиск в ширину (англ. Breadth-First Search, BFS) позволяет вычислить кратчайшие расстояния (в терминах количества рёбер) от выделенной вершины ориентированного графа до всех остальных вершин, и/или построить корневое направленное дерево, расстояния в котором совпадают с расстояниями в исходном графе. Кроме того, поиск в ширину позволяет решать задачу проверки достижимости (существуют ли пути между вершиной источником и остальными вершинами графа). Впервые алгоритм поиска в ширину описан в работах Мура[1] и Ли[2].
Алгоритм основан на обходе вершин графа "по слоям". На каждом шаге есть множество "передовых" вершин, для смежных к которым производится проверка, относятся ли они к еще не посещенным. Все еще не посещенные вершины добавляются в новое множество "передовых" вершин, обрабатываемых на следующем шаге. Изначально в множество "передовых" вершин входит только вершина-источник, от которой и начинается обход.
В последовательном случае алгоритм имеет алгоритмическую сложность [math]O(|V| + |E|)[/math], где [math]|V|[/math] - число вершин в графе, [math]|E|[/math] - число ребер в графе.
1.2 Математическое описание алгоритма
Пусть задан граф [math]G = (V, E)[/math] без весов, и с выделенной вершиной-источником [math]u[/math]. Путем [math]P(u,v)[/math] между вершинами [math]u[/math] и [math]v[/math] называется множество ребер [math](u, v_1), (v_1, v_2), ... (v_{n-1}, v)[/math]. Длиной пути [math]d(u,v)[/math] обозначим число ребер в данном пути между вершинами [math]u[/math] и [math]v[/math]. Поиск в ширину находит кратчайшие пути [math]d(u,v)[/math] от вершины [math]u[/math] до всех остальных вершин графа описанным далее образом.
В начале работы алгоритма расстояние до вершины-источника [math]d(u)=0[/math], до остальных вершин [math]d(v) = \infty, \forall v \neq u [/math]. Также в начале работы алгоритма инициализируется множество [math]F = \{u\}[/math].
Далее на каждом шаге алгоритма строится множество вершин [math]P = {w} [/math], таких, что для [math]\forall v \in F \exists (v, w) \in E | d(w) = \infty [/math], при этом обновляются расстояния [math]d(w)=d(v)+1[/math] для [math]\forall w \in P [/math]. Затем производится переход на следующий шаг до тех пор, пока [math]P \neq \emptyset[/math]; при этом в начале каждого шага множество F заменяется на P.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является обход вершин, смежных с выбранной вершиной [math]v[/math], с последующим добавлением еще не посещенных вершин в множество [math]P[/math]. Данная операция выполняется на каждом шаге для каждой вершины [math]v \in F[/math].
1.4 Макроструктура алгоритма
Алгоритм последовательно уточняет значения функции [math]d(v)[/math].
Структуру можно описать следующим образом:
1. Инициализация: всем вершинам присваивается предполагаемое расстояние [math]d(v)=\infty[/math], кроме вершины-источника, для которой [math]d(u)=0[/math] .
2. Помещение вершины источника [math]v[/math] в множество "передовых" вершин [math]F[/math].
3. Обход вершин множества [math]F[/math].
а) Инициализация множества [math]P=\emptyset[/math].
б) Для каждой вершины [math]v \in F[/math] обход всех вершин [math]w | \exists (v, w)[/math] (смежных с ней), c помещением в множество [math]P[/math] таких вершин [math]w | d(w)=\infty[/math].
в) Замена множества [math]F[/math] на [math]P[/math] и переход на шаг 3 в случае, если множество [math]F \neq \emptyset[/math].
1.5 Схема реализации последовательного алгоритма
Простейшая версия алгоритма поиск в ширину может быть реализована при помощи очередей на языке C++ следующим образом. Код приведен в предположении, что граф хранится в формате сжатого списка смежности: для каждой вершины в массиве vertices_to_edges_ptrs хранятся индекс начала и индекс конца списка смежных с ней вершин из массива dst_ids.
// init distances
for(int i = 0; i < vertices_count; i++)
_result[i] = MAX_INT;
// init queue and first vertex
std::queue<int> vertex_queue;
vertex_queue.push(_source_vertex);
_result[_source_vertex] = 1;
// do bfs
while(vertex_queue.size() > 0)
{
int cur_vertex = vertex_queue.front();
vertex_queue.pop();
long long first = vertices_to_edges_ptrs[cur_vertex];
long long last = vertices_to_edges_ptrs[cur_vertex + 1];
for(long long i = first; i < last; i++)
{
int dst_id = dst_ids[i];
if(_result[dst_id] == MAX_INT)
{
_result[dst_id] = _result[src_id] + 1;
vertex_queue.push(dst_id);
}
}
}
1.6 Последовательная сложность алгоритма
Алгоритм имеет последовательную сложность [math]O(|V| + |E|)[/math], где [math]|V|[/math] и [math]|E|[/math] - число вершин и ребер графа соответственно: алгоритм инициализирует начальный массив расстояний - [math]O(|V|)[/math] операций, а затем обходит каждую вершину один единственный раз - [math]O(|E|)[/math] операций. Данная оценка верна в случае, если формат хранения графа позволяет обходить вершины, смежные к выбранной (к примеру форматы списка смежности, сжатого списка смежности). При использовании других форматов оценка сложности может быть большей.
1.7 Информационный граф
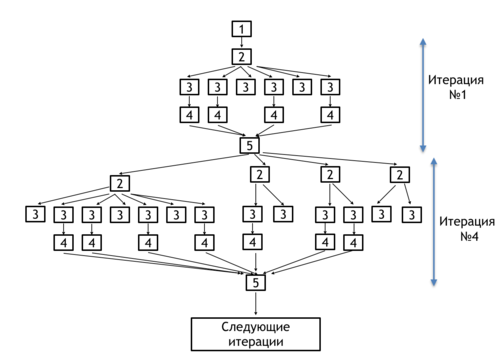
Информационный граф классического алгоритма поиска в ширину приведен на рисунке 1.
На рисунке 1 используются следующие обозначения:
[1] - добавление вершины-источника [math]u[/math] к множеству [math]F[/math].
[2] - извлечение добавленной вершины [math]v[/math] из множества [math]F[/math].
[3] - проверка расстояний до вершин, смежных с вершиной [math]v[/math].
[4] - добавление еще не посещенных вершин в множество [math]P[/math].
[5] - замена множества [math]F[/math] на [math]P[/math] и проверка его пустоты. В случае непустого множества - переход на следующую итерацию, иначе завершение работы алгоритма.
Данный алгоритм имеет один важный недостаток при реализации: операция [4] требует бесконфликтной возможности добавления элементов в множество P, что, на практике, всегда будет сводиться к сериализации обращений к структуре данных, моделирующей данное множество.
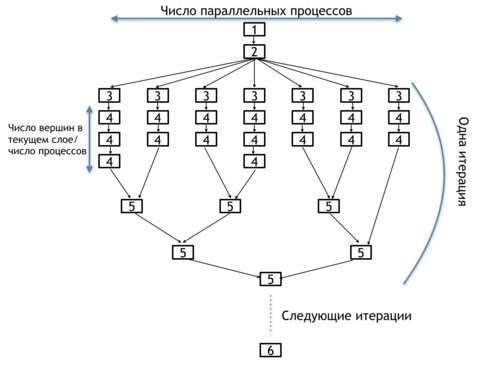
В результате часто используется модификация алгоритма (далее алгоритм-2), использующая набор независимых структур данных для каждого из параллельных процессов. Информационный граф данного подхода приведен на рисунке 2.
Обозначения для рисунка 2:
[1] - добавление вершины-источника в множество [math]F[/math].
[2] - разделение данных множества [math]F[/math] между процессами
[3] - помещение в множества [math]F_i[/math] соответствующих данных из [math]F[/math] каждым процессом с номером i.
[4] - извлечение очередной вершины из множеств [math]F_i[/math], обход её соседей и добавление их в множество [math]P_i[/math] в случае, если они еще не посещены
[5] - попарное слияние множеств [math]P_i[/math] для различных процессов, итоговое преобразование их в множество [math]F[/math].
[6] - проверка условия выхода из цикла
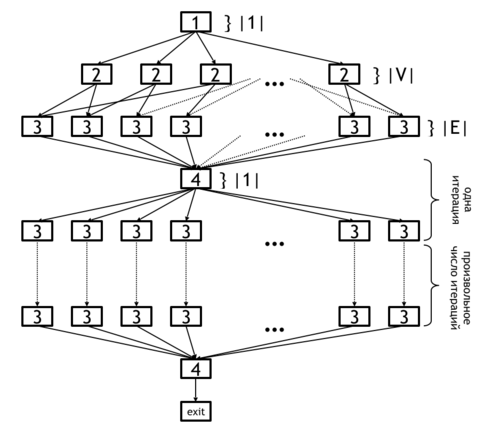
Кроме того, в случае, если реализация структур данных, моделирующих множества [math]F[/math] и [math]P[/math], невозможна, может использоваться квадратичный по сложности алгоритм, схожий с алгоритм Беллмана-Форда. Основная идея заключается в том, что на каждом шаге производится обход всех ребер графа с обновлением текущего массива дистанций. Информационный граф данной модификации алгоритма приведен на рисунке 3.
Обозначения для рисунка 3:
[1] - инициализация расстояний до вершины-источника
[2] - инициализация расстояний до остальных вершин графа
[3] - загрузка информации об очередном ребре и обновление дистанций до соответствующих вершин.
[4] - проверка условия выхода из цикла
1.8 Ресурс параллелизма алгоритма
В ходе работы классический вариант алгоритма обходит граф по слоям. В каждый слой добавляются еще не посещенные вершины, достижимые из вершин предыдущего слоя. Обход вершин каждого слоя, как и их соседей, может производиться параллельно. Точно оценить число вершин в каждом слое невозможно в силу того, что их количество зависит от структуры связанности входного графа. Аналогично невозможно оценить число шагов алгоритма, за которое будут найдены все кратчайшие пути.
Произведем оценку ширины ярусно-параллельной формы алгоритма через максимальное число вершин p в слое среди всех шагов алгоритма. Тогда число параллельных операций на данном слое будет равно сумме числа смежных вершин для каждой вершины слоя: [math]\sum_{n=1}^{p} degree(v_i)[/math], при этом для каждого слоя данное значение будет различным. Высота ярусно-параллельной формы будет равна числу шагов в алгоритме и может быть оценена только сверху (не более [math]|V|[/math]).
При квадратичном подходе к параллельной реализации алгоритма на каждом шаге выполняется [math]O(|E|)[/math] операций, которые могут быть выполнены параллельно; таким образом, ширина ЯПФ данной модификации алгоритма равна [math]O(|E|)[/math]. Число шагов алгоритма, как и в классическом случае, зависит от структуры графа и может быть оценено сверху как [math]O(|V|)[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math], вершина-источник [math]u[/math].
Объём входных данных: [math]O(|V| + |E|)[/math].
Выходные данные (возможные варианты):
- для каждой вершины [math]v[/math] исходного графа расстояние [math]d(v)[/math], определенное как число ребер, лежащих на кратчайшем пути от вершины [math]u[/math] к [math]v[/math].
- для каждой вершины [math]v[/math] исходного графа значение достижимости (достижима или нет) от вершины-источника [math]u[/math].
Объём выходных данных: [math]O(|V|)[/math].