Purdom's, Boost Graph Library: различия между версиями
| [досмотренная версия] | [досмотренная версия] |
ASA (обсуждение | вклад) (Новая страница: «{{level-i}} Основные авторы описания: И.В.Афанасьев = Ссылки = [http://www.boost.org/libs/gr...») |
ASA (обсуждение | вклад) |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 14: | Строка 14: | ||
== Масштабируемость алгоритма == | == Масштабируемость алгоритма == | ||
== Масштабируемость реализации алгоритма == | == Масштабируемость реализации алгоритма == | ||
| + | |||
| + | Для демонстрации эффективности представлены графики времени выполнения различных режимов вычислений в зависимости от размера входного графа. | ||
| + | |||
| + | Основной характеристикой для сравнения было выбрано время выполнения, так как производительность (определенная как TEPS, то есть число ребер графа, которое алгоритм обрабатывает в секунду) для данной операции не отражает реальной ситуации. | ||
| + | |||
| + | Дело в том, что сложность выбранного алгоритма Пурдома зависит от количества ребер в графе нелинейно и, кроме того, зависит еще и от структуры графа (количества сильно связанных компонент). | ||
| + | |||
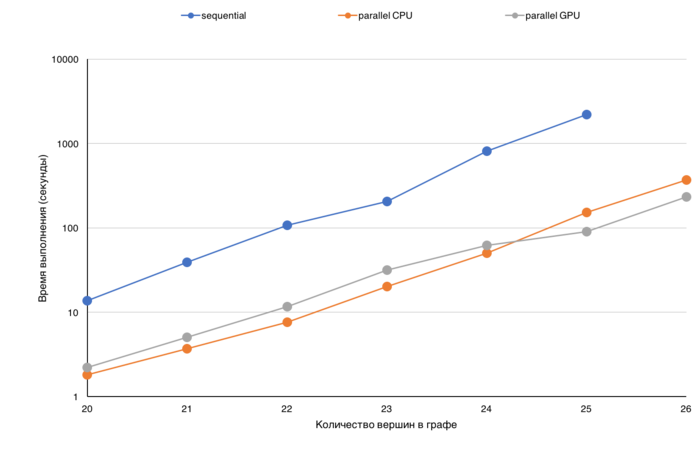
| + | [[file:Замыкание scaling wide.png|thumb|center|700px|Рисунок 1. Параллельная реализация алгоритма Пурдома: масштабируемость различных версий: время выполнения в зависимости от размера графа.]] | ||
| + | |||
| + | Анализируя время выполнения, можно оценить, насколько понижается эффективность обработки графа при увеличении его размера (данные перестают помещаться в кэш, в память GPU, узла и т.д.). На представленных графиках по оси X граф с каждым делением увеличивается в два раза, и по такому графику можно оценивать, насколько увеличилось время выполнения. | ||
| + | Также время выполнения можно сравнивать для различных версий, например, последовательной CPU, параллельной CPU или же GPU. | ||
| + | На приведенной диаграмме (рисунок 1) для различных размеров графа (от 2^20 до 2^26) представлено время выполнения трех различных версий: последовательной, параллельной CPU и GPU. Шкала на данной диаграмме логарифмическая. | ||
| + | |||
= Динамические характеристики и эффективность реализации алгоритма = | = Динамические характеристики и эффективность реализации алгоритма = | ||
= Результаты прогонов = | = Результаты прогонов = | ||
Текущая версия на 12:13, 14 июля 2022
Основные авторы описания: И.В.Афанасьев
Содержание
1 Ссылки
Boost Graph Library (функция transitive_closure).
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
2.1.2 Количественная оценка локальности
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
Для демонстрации эффективности представлены графики времени выполнения различных режимов вычислений в зависимости от размера входного графа.
Основной характеристикой для сравнения было выбрано время выполнения, так как производительность (определенная как TEPS, то есть число ребер графа, которое алгоритм обрабатывает в секунду) для данной операции не отражает реальной ситуации.
Дело в том, что сложность выбранного алгоритма Пурдома зависит от количества ребер в графе нелинейно и, кроме того, зависит еще и от структуры графа (количества сильно связанных компонент).
Анализируя время выполнения, можно оценить, насколько понижается эффективность обработки графа при увеличении его размера (данные перестают помещаться в кэш, в память GPU, узла и т.д.). На представленных графиках по оси X граф с каждым делением увеличивается в два раза, и по такому графику можно оценивать, насколько увеличилось время выполнения. Также время выполнения можно сравнивать для различных версий, например, последовательной CPU, параллельной CPU или же GPU. На приведенной диаграмме (рисунок 1) для различных размеров графа (от 2^20 до 2^26) представлено время выполнения трех различных версий: последовательной, параллельной CPU и GPU. Шкала на данной диаграмме логарифмическая.