K-means clustering, scalability2: различия между версиями
| [досмотренная версия] | [досмотренная версия] |
ASA (обсуждение | вклад) (Новая страница: «{{level-i}} Основные авторы описания: [https://algowiki-project.org/ru/Участник:IanaV<b>Я.А.Валуйская</b>], [https://alg...») |
ASA (обсуждение | вклад) |
||
| Строка 48: | Строка 48: | ||
[[Категория:Статьи в работе]] | [[Категория:Статьи в работе]] | ||
| − | [[En:K-means clustering, scalability2 | + | [[En:K-means clustering, scalability2]] |
Текущая версия на 16:14, 19 июля 2022
Основные авторы описания: Я.А.Валуйская, Е.С.Глотов.
Содержание
1 Ссылки
Исследовалась параллельная реализация алгоритма k-means на MPI.
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
2.1.2 Количественная оценка локальности
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
Исследование проводилось на суперкомпьютере "Ломоносов"[1] Суперкомпьютерного комплекса Московского университета.
Набор данных для тестирования состоял из 946000 векторов размерности 2 (координаты на сфере)
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессов (виртуальных ядер) [8 : 512];
- число кластеров [128 : 384].
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации [math]2,47%[/math] достигается при делении исходных данных на 128 кластеров с использованием 512 процессов;
- максимальная эффективность реализации [math]7,13%[/math] достигается при делении исходных данных на 352 кластера с использованием 8 процессов.
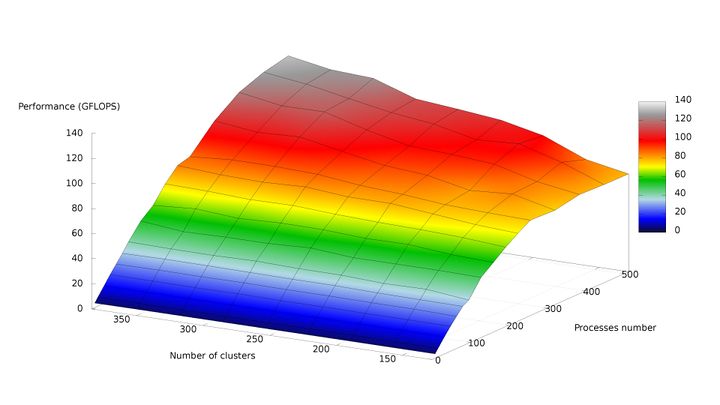
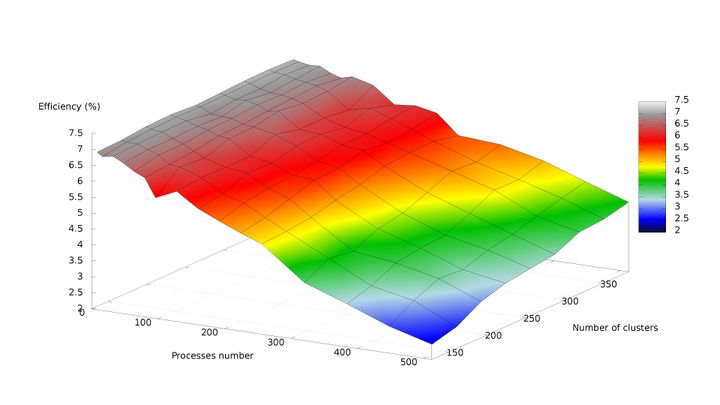
На рисунках 1 и 2, соответственно, представлены графики зависимости производительности и эффективности параллельной реализации k-means от числа кластеров и числа процессов.
По рис. 1 можно отметить практически полное отсутствие роста производительности с увеличением числа процессов от 256 до 512 при минимальном размере задачи. Это связано с быстрым ростом накладных расходов по отношению к крайне низкому объёму вычислений. При росте размерности задачи данный эффект пропадает, и при одновременном пропорциональном увеличении числа кластеров и числа процессов рост производительности становится близким к линейному.
Были получены следующие оценки масштабируемости реализации алгоритма k-means:
- По числу процессов: [math]-0.02209[/math]. Следовательно, с ростом числа процессов эффективность уменьшается. На рис. 7 можно наблюдать плавное и равномерное снижение производительности по мере увеличения числа процессов при неизменном числе кластеров, что свидетельствует об относительно невысоком росте накладных расходов на передачу данных между процессами и преобладании объёма вычислений над объёмом пересылок данных по сети.
- По размеру задачи: [math]0.01252[/math]. Следовательно, с ростом размера задачи (числа кластеров) эффективность увеличивается. При этом объём пересылок данных по сети пропорционален [math](n + k) \cdot p[/math] (где [math]k[/math] - число кластеров, [math]n[/math] - число входных векторов, [math]p[/math] - число процессов) таким образом, поскольку [math]k \lt \lt n[/math], рост накладных расходов с ростом числа кластеров при неизменном числе процессов и входных векторов представляет собой незначительную величину.
- Общая оценка: [math]-0.00081[/math]. Таким образом, с ростом и размера задачи, и числа процессов эффективность уменьшается. Это связано с тем, что отношение объёма вычислений к объёму передаваемых данных изменяется пропорционально [math]{kn \over (n + k) \cdot p} \thicksim {k \over p}[/math], что представляет собой невысокий коэффициент, но при этом позволяет параллельной реализации не деградировать до нулевой эффективности при значительном увеличении числа процессов.
4 Динамические характеристики и эффективность реализации алгоритма
5 Результаты прогонов
6 Литература
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.