Метод Ньютона для систем нелинейных уравнений: различия между версиями
| [досмотренная версия] | [досмотренная версия] |
ASA (обсуждение | вклад) |
Slava (обсуждение | вклад) м (Add \Delta x^{(k)} in two equations.) |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 68: | Строка 68: | ||
Основная сложность метода Ньютона заключается в обращении матрицы Якоби. Вводя обозначение <math>\Delta x^{(k)} = x^{(k+1)} - x^{(k)}</math> получаем СЛАУ для вычисления <math>\Delta x^{(k)}:</math> | Основная сложность метода Ньютона заключается в обращении матрицы Якоби. Вводя обозначение <math>\Delta x^{(k)} = x^{(k+1)} - x^{(k)}</math> получаем СЛАУ для вычисления <math>\Delta x^{(k)}:</math> | ||
| − | <math>\frac{\partial{F(x^{(k)})}}{\partial{x}} = -F(x^{(k)})</math> | + | <math>\frac{\partial{F(x^{(k)})}}{\partial{x}} \Delta x^{(k)} = -F(x^{(k)})</math> |
Тогда <math>x^{(k+1)} = x^{(k)}+ \Delta x^{(k)}.</math> | Тогда <math>x^{(k+1)} = x^{(k)}+ \Delta x^{(k)}.</math> | ||
| Строка 76: | Строка 76: | ||
При <math>n_i \le k < n_{i+1}</math> вычисление <math>\Delta x^{(k)}</math> осуществляют по следующей формуле: | При <math>n_i \le k < n_{i+1}</math> вычисление <math>\Delta x^{(k)}</math> осуществляют по следующей формуле: | ||
| − | <math>\frac{\partial{F(x^{n_i})}}{\partial{x}} = -F(x^{(k)}).</math> | + | <math>\frac{\partial{F(x^{n_i})}}{\partial{x}} \Delta x^{(k)} = -F(x^{(k)}).</math> |
Увеличение числа итераций, сопровождающее такую модификацию, компенсируется «дешевизной» одного шага итерации. | Увеличение числа итераций, сопровождающее такую модификацию, компенсируется «дешевизной» одного шага итерации. | ||
| Строка 205: | Строка 205: | ||
== Литература == | == Литература == | ||
| − | <references | + | <references /> |
[[Категория:Статьи в работе]] | [[Категория:Статьи в работе]] | ||
[[en:Newton's method for systems of nonlinear equations]] | [[en:Newton's method for systems of nonlinear equations]] | ||
Текущая версия на 00:17, 4 декабря 2022
Основные авторы статьи:
К.О.Шохин и
А.А.Лебедев,
О.Р.Гирняк и
Д.А.Васильков (раздел 1.7).
| Метод Ньютона решения систем нелинейных уравнений | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(L \cdot n^3)[/math], если для решения СЛАУ использовать метод Гаусса, алгоритм сойдется за [math]L[/math] итераций, вычисление значения каждой функции системы и их производных в точке имеет оценку сложности [math]O(n)[/math] |
| Объём входных данных | [math]n[/math] функций от [math]n[/math] переменных, [math]n^2[/math] частных производных этих функций по каждой переменной, [math]n[/math]-мерный вектор(начальное приближение решения), [math]\varepsilon[/math] - требуемая точность, [math]{\rm max\_iter}[/math] - максимальное число итераций |
| Объём выходных данных | [math]n[/math]-мерный вектор |
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод Ньютона[1][2] решения систем нелинейных уравнений является обобщением метода Ньютона решения нелинейных уравнений, который основан на идее линеаризации. Пусть [math] F(x) : {\mathbb R}^1 \to {\mathbb R}^1[/math] - дифференцируемая функция и необходимо решить уравнение [math]F(x) = 0[/math].
Взяв некоторое [math]x_0[/math] в качестве начального приближения решения, мы можем построить линейную аппроксимацию
[math]F(x)[/math] в окрестности [math]x_0 : F(x_0+h) \approx F(x_0)+F^\prime(x_0)h[/math] и решить получающееся линейное уравнение [math]F(x_0 )+F^\prime (x_0 )h =0[/math].
Таким образом получаем итеративный метод : [math] x_{k+1} = x_k - {F^\prime(x_k)}^{-1}F(x_k), \ k = 0,1,\ldots [/math] .
Данный метод был предложен Ньютоном в 1669 году[3]. Более точно, Ньютон оперировал только с полиномами; в выражении для [math]F(x+h)[/math] он отбрасывал члены более высокого порядка по h , чем линейные. Ученик Ньютона Рафсон в 1690 г. предложил общую форму метода (т. е. не предполагалось что [math]F(x)[/math] обязательно полином и использовалось понятие производной), поэтому часто говорят о методе Ньютона—Рафсона. Дальнейшее развитие исследований связано с именами таких известных математиков, как Фурье, Коши и другие. Например, Фурье доказал в 1818 г., что метод сходится квадратично в окрестности корня, а Коши (1829, 1847) предложил многомерное обобщение метода и использовал метод для доказательства существования решения уравнения.
1.2 Математическое описание алгоритма
Пусть дана система из [math]n[/math] нелинейных уравнений с [math]n[/math] неизвестными.
[math] \left\{\begin{matrix} f_1(x_1, \ldots, x_n) = 0, \\ f_2(x_1, \ldots, x_n) = 0, \\ \vdots \\ f_n(x_1, \ldots, x_n) = 0. \end{matrix}\right. [/math] , где [math]f_i(x_1, \ldots,x_n) : {\mathbb R}^n \to {\mathbb R}, \ i = 1,\ldots,n[/math] - нелинейные функции, определенные и непрерывно дифференцируемые в некоторой области [math]G \subset {\mathbb R}^n[/math].
Запишем ее в векторном виде:
[math]\overline{x} = {(x_1,x_2,\ldots,x_n)}^T, F(x) ={[f_1(x),f_2(x),\ldots,f_n(x)]}^T, F(x)=0[/math]
Требуется найти такой вектор [math]\overline{x^*} = {(x^*_1,x^*_2,\ldots,x^*_n)}^T[/math], который, при подстановке в исходную систему, превращает каждое уравнение в верное числовое равенство.
При таком подходе формула для нахождения решения является естественным обобщением формулы одномерного итеративного метода:
[math]x^{(k+1)} = x^{(k)} - W^{-1}(x^{(k)})\cdot F(x^{(k)}) , k=0,1,2,\ldots[/math], где
[math] W = \begin{pmatrix} \frac{\partial{f_1(x_1)}}{\partial{x_1}} & \cdots & \frac{\partial{f_1(x_n)}}{\partial{x_n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial{f_n(x_1)}}{\partial{x_1}} & \cdots & \frac{\partial{f_n(x_n)}}{\partial{x_n}} \end{pmatrix}[/math] – матрица Якоби.
В рассмотренных предположениях относительно функции [math]F(\cdot)[/math] при выборе начального приближения [math]x^{(0)}[/math] из достаточно малой окрестности решения [math]\overline{x^*}[/math] имеет место сходимость последовательности [math]\{x^{(k)}\}[/math]. При дополнительном предположении [math]F(\cdot) \in C^2[/math] имеет место квадратичная сходимость метода.
В качестве критерия окончания процесса итераций обычно берут условие [math]\left \| x^{(k+1)} - x^{(k)} \right \| \lt \varepsilon[/math], где [math]\varepsilon[/math] - требуемая точность решения.
Основная сложность метода Ньютона заключается в обращении матрицы Якоби. Вводя обозначение [math]\Delta x^{(k)} = x^{(k+1)} - x^{(k)}[/math] получаем СЛАУ для вычисления [math]\Delta x^{(k)}:[/math] [math]\frac{\partial{F(x^{(k)})}}{\partial{x}} \Delta x^{(k)} = -F(x^{(k)})[/math]
Тогда [math]x^{(k+1)} = x^{(k)}+ \Delta x^{(k)}.[/math]
Часто метод Ньютона модифицируют следующим образом. По ходу вычислений или заранее выбирают возрастающую последовательность чисел [math]n_0=0, n_1,\ldots[/math]
При [math]n_i \le k \lt n_{i+1}[/math] вычисление [math]\Delta x^{(k)}[/math] осуществляют по следующей формуле:
[math]\frac{\partial{F(x^{n_i})}}{\partial{x}} \Delta x^{(k)} = -F(x^{(k)}).[/math]
Увеличение числа итераций, сопровождающее такую модификацию, компенсируется «дешевизной» одного шага итерации.
1.3 Вычислительное ядро алгоритма
Основная вычислительная нагрузка алгоритма заключается в решении СЛАУ:
[math]\frac{\partial F(x^{(k)})}{\partial x}\Delta x^{(k)} = -F(x^{(k)}) \qquad (1)[/math]
Для нахождения [math]\Delta x^{(k)}[/math], по которому вычисляется значение вектора [math]\overline{x}[/math] на очередной итерации: [math]x^{(k+1)} = x^{(k)} + \Delta x^{(k)}.[/math]
1.4 Макроструктура алгоритма
Как уже было сказано, основную часть каждой итерации метода составляет нахождение матрицы Якоби и решение СЛАУ [math](1)[/math] для нахождения [math]\Delta x^{(k)}.[/math]
1.5 Схема реализации последовательного алгоритма
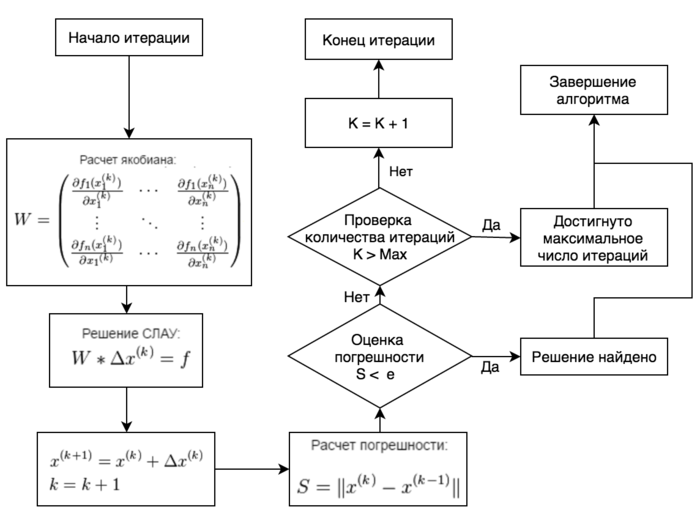
Формулы метода описаны выше. На рис 1. представлена блок-схема алгоритма, в которой:
- [math]n[/math] - число уравнений в СЛАУ
- Max - предельное число итераций
- [math]\varepsilon[/math] - точность вычислений
- [math]x^{(0)}[/math] - начальное приближение
1.6 Последовательная сложность алгоритма
Пусть вычисление значения первой производной функции [math]f_i(x_1,x_2,\ldots,x_n)[/math] в точке [math]x^{(k)}[/math] имеет оценку сложности [math]D_i[/math], решение СЛАУ [math](1)[/math] имеет оценку сложности [math]S[/math] (в эту оценку также включаются операции по нахождению элементов матрицы Якоби), а оценка сложности сложения векторов – [math]V[/math]. Тогда оценка сложности одной итерации представляется в виде:
[math]\sum^{n}_{i=1} {D_i} + S + V[/math]
Количество итераций определяется скоростью сходимости алгоритма. Скорость сходимости метода Ньютона в общем случае является квадратичной. Однако успех или неуспех применения алгоритма во многом определяется выбором начального приближения решения. Если начальное приближение выбрано достаточно хорошо и матрица системы линейных уравнений на каждой итерации хорошо обусловлена и имеет обратную матрицу, то метод Ньютона сходится к единственному в данной окрестности решению. На практике критерием работоспособности метода является число итераций: если оно оказывается большим (для большинства задач >100), то начальное приближение выбрано плохо.
В качестве примера можно рассмотреть алгоритм Ньютона, использующий для решения СЛАУ метод Гаусса. Рассмотрим решение системы, для которой справедливы следующие предположения:
- Вычисление значения каждой функции в заданной точке требует [math]O(n)[/math] операций.
- Вычисление значения производной каждой функции в заданной точке требует [math]O(n)[/math] операций.
В таких предположениях указанное выражение для вычисления сложности примет следующий вид:
[math]O(n^2) + O(n^3) + O(n) = O(n^3)[/math]
Предположим также, что выполнены все условия для квадратичной сходимости метода, и для решения системы потребуется небольшое (<100) количество итераций.
Пусть алгоритм сойдется за [math]L[/math] итераций, тогда итоговая сложность будет равна [math]O(L \cdot n^3)[/math].
1.7 Информационный граф
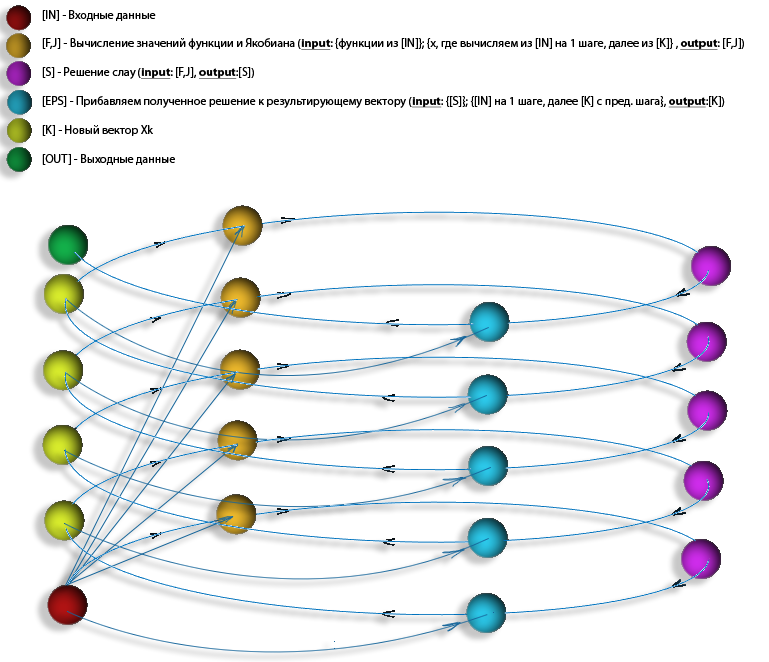
На рис. 2 изображена структура информационного графа алгоритма. Блок IN представляет собой выбор начального приближения, необходимой точности. Каждый блок IT соответствует одной итерации алгоритма, блок-схема итерации алгоритма представлена на рис. 3. Блок OUT соответствует успешному окончанию алгоритма.
Как видно, алгоритм является строго последовательным, каждая итерация зависит от результата предыдущей.
Информационный граф метода Ньютона может быть также представлен в виде следующего рисунка:
1.8 Ресурс параллелизма алгоритма
Хотя сам по себе алгоритм и является строго последовательным, в нем все же присутствует возможность ускорить выполнение за счет распараллеливания отдельных этапов. Основной ресурс параллелизма заключен в решении СЛАУ [math](1)[/math]. Применять можно любой из известных алгоритмов, ориентируясь на известные особенности структуры матрицы Якоби исходной системы.
В качестве примера рассмотрим метод Ньютона, использующий для решения СЛАУ параллельный вариант метода Гаусса, в котором между процессорами распределяются строки исходной матрицы. Оставаясь в тех же предположениях, что были сделаны при вычислении оценки последовательной сложности, получим оценку параллельной сложности алгоритма.
Пусть задача решается на [math]p[/math] процессорах, тогда сложность решения СЛАУ имеет оценку [math]O(\frac{n^3}{p})[/math].
Теперь каждому процессору нужно вычислить не [math]n[/math], а [math]\frac{n}{p}[/math] функций, поэтому для вычисления элементов матрицы Якоби и правой части СЛАУ потребуется [math]O(\frac{n^2}{p})[/math] операций.
Таким образом, получаем следующую оценку параллельной сложности одной итерации алгоритма: [math]O(\frac{n^2}{p}) + O(\frac{n^3}{p}) + O(n) = O(\frac{n^3}{p})[/math].
Пусть алгоритм сходится за [math]L[/math] итераций, тогда итоговая сложность будет равна [math]O(L \cdot \frac{n^3}{p})[/math].
1.9 Входные и выходные данные алгоритма
При определении объема входных и выходных данных алгоритма будем придерживаться следующих предположений:
- Рассматривается 64-битная система, таким образом каждый адрес занимает 64 бита.
- Все числа, с которыми оперирует алгоритм также занимают 64 бита.
- Каждая функция будет представлена своим адресом, таким образом вклад функций в объем входных данных будет равен [math]n[/math] чисел.
- Производная каждой функции также представлена своим адресом, и вклад производных в объем входных данных будет равен [math]n^2[/math] чисел.
Входными данными алгоритма являются:
- Функции, образующие систему уравнений.
- Производные функций, образующих систему уравнений, если их можно задать аналитически.
- Точность, с которой требуется найти решение.
- Максимальное число итераций, которое может быть проделано.
- Начальное приближение [math]x^{(0)}[/math].
Объем входных данных алгоритма равен [math]n ^2 + 2\cdot n + 2 [/math] в случае, когда на вход алгоритму передаются частные производные ([math]n^2[/math] адресов частных производных [math]n[/math] функций по [math]n[/math] переменным, [math]n[/math] адресов функций, образующих систему уравнений, [math]n[/math]-мерный вектор начального приближения, требуемая точность и максимальное количество итераций), когда частные производные приближенно вычисляются непосредственно в программе, объем входных данных равен [math]2\cdot n + 2.[/math]
Выходными данными алгоритма в случае успеха является вектор, который удовлетворяет решению СЛАУ с заданной точностью, в случае выхода количества итераций за заданное ограничение, считается, что алгоритм не смог найти удовлетворяющее ограничениям решение, и выдается сообщение об ошибке.
Объем выходных данных: [math]n.[/math]
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложностей зависит от того, какие алгоритмы применяются для решения СЛАУ [math](1)[/math]. Результат работы алгоритма сильно зависит от выбора начального приближения решения. При удачном выборе алгоритм достаточно быстро сходится к искомому решению. Глобальная сходимость для многих задач отсутствует.
Существует теорема о достаточном условии сходимости метода Ньютона:
Пусть функция [math]F(x)[/math] непрерывно дифференцируема в открытом выпуклом множестве [math]G \subset {\mathbb R}^n[/math]. Предположим, что существуют [math]\overline{x^*} \in {\mathbb R}^n[/math] и [math]r,\beta \gt 0 [/math], такие что [math]N(\overline{x^*},r) \subset G , F(\overline{x^*}) = 0[/math] , и существует [math]W^{-1}(\overline{x^*})[/math], причем [math]\left \| W^{-1}(\overline{x^*})\right \| \le \beta [/math] и [math]W(x) \in Lip_{\gamma} (N(\overline{x^*},r))[/math]. Тогда существует [math]\varepsilon \gt 0[/math] такое, что для всех [math]x^{(0)} \in N(\overline{x^*}, \varepsilon)[/math] последовательность [math]x^{(1)},x^{(2)},\ldots[/math] порождаемая итерационным процессом сходится к [math]\overline{x^*}[/math] и удовлетворяет неравенству [math]\left \|x^{(k+1)} - \overline{x^*}\right \| \le \beta\cdot\gamma\cdot{\left \| x^{(k)}- \overline{x^*}\right \|}^2[/math].
Использовались следующие обозначения:
- [math]N(x,r)[/math] - открытая окрестность радиуса [math]r[/math] с центром в точке [math]x[/math];
- [math]W(x) \in Lip_{\gamma}(N(x,r))[/math] означает, что [math]W(x)[/math] непрерывна по Липшицу с константой [math]\gamma[/math] в области [math]N(x,r)[/math].
Оставаясь в предположениях, описанных при вычислении объема входных данных, имеем объем входных данных равный [math]n^2 + 2\cdot n + 2 = O(n^2)[/math] чисел.
Оценку числа операций возьмем для реализации метода Ньютона с помощью метода Гаусса: [math]O(n^3)[/math]. Тогда вычислительная мощность есть [math]O(n)[/math].
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Возможные способы и особенности параллельной реализации алгоритма
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
3 Литература
- ↑ Тыртышников Е. Е. "Методы численного анализа" — М., Академия, 2007. - 320 c.
- ↑ Бахвалов Н. С., Жидков Н. П., Кобельков. Г. М. "Численные Методы" — 6-е изд. — М. : БИНОМ. Лаборатория знаний, 2008. — 636 с.
- ↑ Поляк Б. Т. "Метод Ньютона и его роль в оптимизации и вычислительной математике" - Труды ИСА РАН 2006. Т. 28