Уровень алгоритма

Участник:Маркова Екатерина/Построение матрицы Адамара: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
 
(не показано 75 промежуточных версий 2 участников)
Строка 1: Строка 1:
 +
{{Assignment|Sleo}}
 +
{{algorithm
 +
| name              = Построение матрицы Адамара
 +
| serial_complexity = <math>O(N^2)</math>
 +
| pf_height        = <math>O(m)</math>
 +
| pf_width          = <math>4</math>
 +
| input_data        = <math>1</math>
 +
| output_data      = <math>N^2</math>
 +
}}
 +
Основной автор статьи: Маркова Е.А. 615 гр.
 +
== Свойства и структура алгоритма ==
 +
=== Общее описание алгоритма===
 +
 +
Матрица Адамара <math>H</math> - это квадратная матрица размера <math>N\times N</math>, составленная из чисел <math>1</math> и <math>-1</math>, столбцы которой ортогональны, так что справедливо соотношение:
 +
 +
<math>H*H^T = N*E_N</math>,
 +
 +
где <math>E_N</math> - это единичная матрица размера <math>N</math>. Матрицы Адамара применяются в различных областях, включая комбинаторику, численный анализ, обработку сигналов.
  
−
== Свойства и структура алгоритма ==
+
Предложенный алгоритм является рекурсивным и описывает получение матриц Адамара только порядка степени 2. На каждом следующем шаге алгоритма, новая матрица составляется из матрицы, полученной на предыдущем этапе, путем заполнения соответствующих блоков.
−
'''1.1 Общее описание алгоритма'''
+
 
 +
=== Математическое описание алгоритма ===
 +
 
 +
Пусть <math>H_m</math> <math>-</math> матрица Адамара порядка <math>2^m</math> и <math>-H_m</math> <math>-</math> матрица с противоположными элементами. Тогда матрица <math>H_{2m}</math> получается следующим образом:
 +
<math>H_{2m} = \begin{bmatrix}
 +
        H_m & H_m \\
 +
        H_m & -H_m
 +
      \end{bmatrix}
 +
</math>
 +
 
 +
Данным алгоритм описывает получение матриц Адамара только порядка степени 2, то есть <math>m</math> и <math>N</math> связаны соотношением <math>N = 2^m</math>.
 +
 
 +
Получение матрицы порядка <math>N</math> состоит из следующих <math>m</math> шагов:
 +
 
 +
Шаг 1: <math>H_1 = (1);</math>
 +
 
 +
Шаг 2: <math>H_2 =
 +
\begin{pmatrix} 1 & 1
 +
\\1 & -1
 +
\end{pmatrix};
 +
</math>
 +
 
 +
Шаг 3: <math>H_3 =
 +
\begin{pmatrix} 1 & 1 & 1 & 1
 +
\\1 & -1 & 1 & -1
 +
\\1 & 1 &- 1 & -1
 +
\\1 & -1 & -1 & 1
 +
\end{pmatrix}.
 +
</math>
 +
 
 +
...
 +
 
 +
Шаг <math>m</math>: искомая матрица <math>H_m</math>.
 +
 
 +
=== Вычислительное ядро алгоритма ===
 +
 
 +
Вычислительное ядро рекурсивного алгоритма состоит из  <math>\;N^2\;</math>  присвоений значений матрицы Адамара
 +
 
 +
<math>H_{1,1} = 1</math>;
  
−
'''1.2 Математическое описание алгоритма'''
+
<math>H_{ij} = H_{i(j - \frac{N}{2})}</math>, где <math>i = 1..\frac{N}{2}</math>, <math>j = \frac{N}{2}+1..N</math>;
  
−
'''1.3 Вычислительное ядро алгоритма'''
+
<math>H_{ij} = H_{(i-\frac{N}{2})j}</math>, где <math>i = \frac{N}{2}+1..N</math>, <math>j = 1.. \frac{N}{2}</math>;
  
−
Вычислительное ядро рекурсивного алгоритма состоит из  <math>\;\frac{N^2}{2}\;</math> переносов значений в повторяющиеся блоки матрицы и  <math>\frac{N^2}{4}</math> переносов со сменой знака (умножением на <math>-1</math>).
+
<math>H_{ij} = H_{(i-\frac{N}{2})(j-\frac{N}{2})}</math>, где <math>i = \frac{N}{2}+1..N </math>, <math>j = \frac{N}{2}+1..N</math>.
  
−
'''1.4 Макроструктура алгоритма'''
+
=== Макроструктура алгоритма ===
  
 
Алгоритм не использует в качестве составных частей другие алгоритмы. Как это было описано в вычислительном ядре, в пустые блоки дублируются со сменой или без смены знака значения первого блока матрицы.  
 
Алгоритм не использует в качестве составных частей другие алгоритмы. Как это было описано в вычислительном ядре, в пустые блоки дублируются со сменой или без смены знака значения первого блока матрицы.  
  
−
'''1.5 Схема реализации последовательного алгоритма'''
+
=== Схема реализации последовательного алгоритма===
  
 
В описанном  виде алгоритм представляет из себя примитивное дублирование элементов матрицы, полученной на предыдущем этапе, в пустующие блоки новой матрицы.
 
В описанном  виде алгоритм представляет из себя примитивное дублирование элементов матрицы, полученной на предыдущем этапе, в пустующие блоки новой матрицы.
  
−
Сначала заполняется правый верхний блок матрицы <math>h</math>
+
Сначала заполняется правый верхний блок матрицы <math>H</math>
  
−
<math>h_{ij} = h_{i(j - \frac{N}{2})}</math>, где <math>i = 1..\frac{N}{2}</math>, <math>j = \frac{N}{2}+1..N</math>;
+
<math>H_{ij} = H_{i(j - \frac{N}{2})}</math>, где <math>i = 1..\frac{N}{2}</math>, <math>j = \frac{N}{2}+1..N</math>;
  
 
затем левый нижний блок
 
затем левый нижний блок
  
−
<math>h_{ij} = h_{(i-\frac{N}{2})j}</math>, где <math>i = \frac{N}{2}+1..N</math>, <math>j = 1.. \frac{N}{2}</math>.
+
<math>H_{ij} = H_{(i-\frac{N}{2})j}</math>, где <math>i = \frac{N}{2}+1..N</math>, <math>j = 1.. \frac{N}{2}</math>.
  
 
Последним заполняется нижний правый блок матрицы
 
Последним заполняется нижний правый блок матрицы
  
−
<math>h_{ij} = h_{(i-\frac{N}{2})(j-\frac{N}{2})}</math>, где <math>i = \frac{N}{2}+1..N </math>, <math>j = \frac{N}{2}+1..N</math>.
+
<math>H_{ij} = H_{(i-\frac{N}{2})(j-\frac{N}{2})}</math>, где <math>i = \frac{N}{2}+1..N </math>, <math>j = \frac{N}{2}+1..N</math>.
 +
 
 +
 
 +
=== Последовательная сложность алгоритма===
 +
 
 +
Для заполнения  матрицы <math>H</math> размера <math>N\times N</math> необходимо <math>\;N^2\;</math>  присвоений значений. Из чего можно сделать вывод, что рекурсивный метод построения матрицы Адамара является алгоритмом с ''квадратичной сложностью''.
 +
 
 +
===Информационный граф===
 +
 
 +
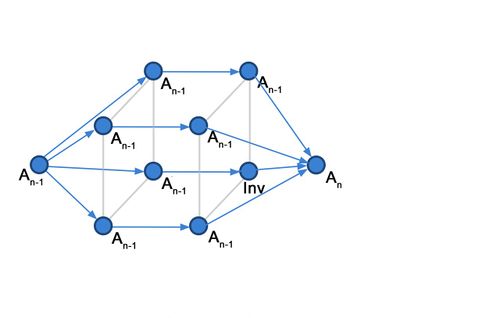
[[file:111.jpeg|thumb|center|500px|Рисунок 1. Граф отображает шаг, стрелками показаны пересылки данных, в узлах происходит операция присвоения значений и инверсия.]]
 +
 
 +
=== Ресурс параллелизма алгоритма===
 +
 
 +
Логически алгоритм можно разделить на три части, которые на каждом шаге выполняются независимо.
 +
Внутри каждой части происходит <math>2^{2N}-2^{2(N-1)}</math> независимых присвоений, где <math>N</math> - номер шага алгоритма, причем размерность матрицы на шаге <math>N</math> равна <math>2^N</math>. При этом необходимо ждать завершения предыдущего шага, то есть необходимы синхронизирующие блокировки.
 +
 
 +
===Входные и выходные данные алгоритма===
  
 +
Входные данные: <math>N</math> - размерность матрицы.
  
−
'''1.6 Последовательная сложность алгоритма'''
+
Объем входных данных: 1.
  
−
Для заполнения трех пустых блоков равного размера матрицы <math>h</math> размера <math>N\times N</math> необходимо <math>\frac{3N^2}{4}</math>.
+
Выходные данные: матрица размером <math>N\times N</math>.
  
−
'''1.7 Информационный граф'''
+
Объем выходных данных: <math> N^2</math>.
  
−
'''1.8 Ресурс параллелизма алгоритма'''
+
===Свойства алгоритма===
 +
Вычислительная мощность алгоритма равна суммарному объему входных и выходных данных: <math>N^2 + 1</math>.
  
−
'''1.9 Входные и выходные данные алгоритма'''
+
Алгоритм полностью детерминирован.
  
−
'''1.10 Свойства алгоритма'''
+
Не смотря на существование недоказанной гипотезы, что существует алгоритм, способный построить матрицы Адамара, размера кратного 4, данный алгоритм вычисляет только матрицы размера степени 2.
  
 
== Программная реализация алгоритма ==
 
== Программная реализация алгоритма ==
 +
 +
===Особенности реализации последовательного алгоритма===
 +
=== Локальность данных и вычислений ===
 +
=== Возможные способы и особенности параллельной реализации алгоритма ===
 +
=== Масштабируемость алгоритма и его реализации ===
 +
 +
Исследование проводилось на [http://cluster2.inm.ras.ru кластере ИВМ].
 +
 +
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
 +
 +
* число процессоров [1:32];
 +
* размер матрицы [32: 16384].
 +
 +
В результате проведённых экспериментов был получен следующий диапазон эффективности алгоритма:
 +
 +
* минимальная эффективность реализации 0,016%;
 +
* максимальная эффективность реализации 92%.
 +
 +
На следующих рисунках приведены графики производительности и эффективности выбранной реализации построения Матрицы Адамара в зависимости от изменяемых параметров запуска.
 +
 +
Построим оценки масштабируемости выбранной реализации построения матрицы Адамара:
 +
* По числу процессоров:
 +
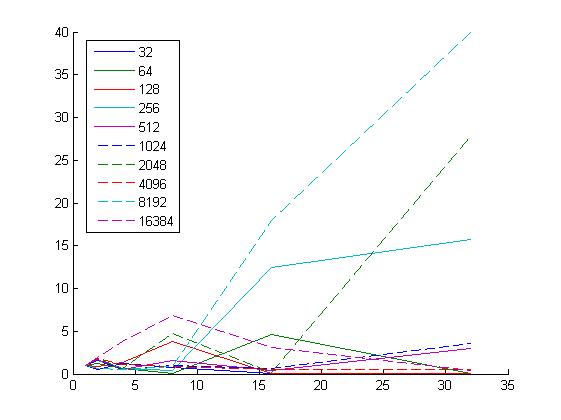
[[Файл:EQP8kY4D9E0.jpg|thumb|center|700px|Рисунок 2. Масштабируемость по числу процессоров. По оси ОХ отложено количество процессоров, по оси ОУ - величина производительности для разного размера матрицы.]]
 +
* По размеру задачи:
 +
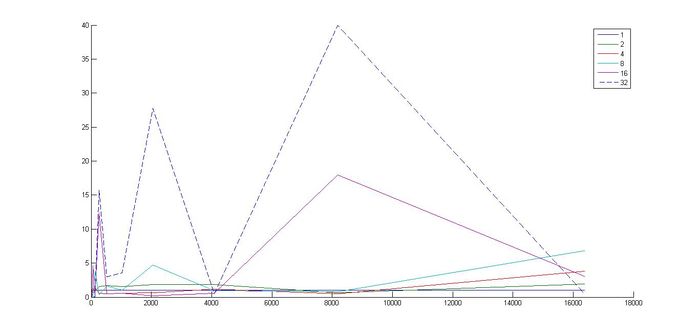
[[Файл:PmIAoJaqnO8.jpg|thumb|center|700px|Рисунок 3. Масштабируемость по размеру задачи. По оси ОХ отложена размерность матрицы, по оси ОУ - величина производительности для разного количества процессоров]]
 +
* По двум направлениям:
 +
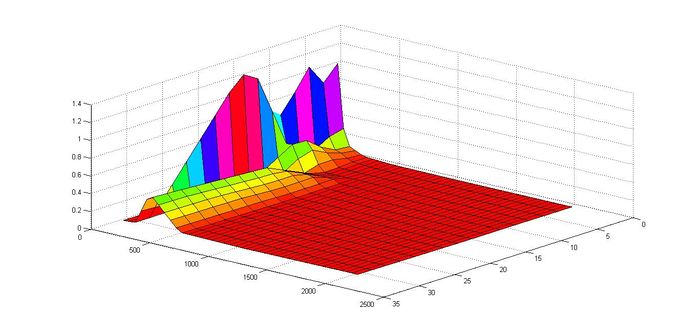
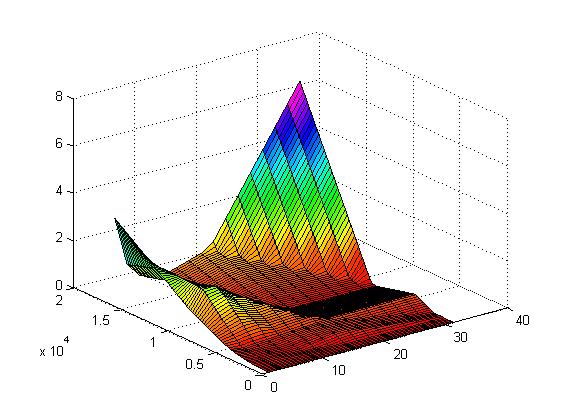
[[Файл:Khm.jpg|thumb|center|700px|Рисунок 4. Масштабируемость по двум направлениям. По ОХ - количество процессоров, по ОУ - размерность матрицы, по OZ - величина производительности при изменении в двух направлениях.]]
 +
[[Файл:untitled.jpg|thumb|center|700px|Рисунок 5. Параллельная реализация построения матрицы Адамара. Изменение производительности в зависимости от числа процессоров и размера матрицы.]]
 +
 +
[https://www.dropbox.com/s/1ga1fp26nztt65n/hadamard_2.c?dl=0 Исследованная реализация на языке C]
 +
 +
=== Динамические характеристики и эффективность реализации алгоритма ===
 +
=== Выводы для классов архитектур ===
 +
=== Существующие реализации алгоритма ===
 +
 +
Реализация
 +
[https://www.mathworks.com/help/matlab/ref/hadamard.html?requestedDomain=www.mathworks.com MATLAB]
 +
 +
Реализация
 +
[http://pydoc.net/Python/rogues/0.3.0/rogues.matrices.hadamard/ PYTHON]
 +
 +
Реализация
 +
[https://reference.wolfram.com/language/ref/HadamardMatrix.html WOLFRAM]
 +
 +
На языке ''Java'' реализован класс ''Hadamard'' не входящий в стандарт языка. С кодом можно ознакомиться по [https://gist.github.com/guitarkitten/3937264 ссылке].
 +
 +
== Литература ==
 +
1. Мак-Вильямс Ф., Слоэн Н. — "Теория кодов, исправляющих ошибки" (1979)
 +
 +
2. Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — "Алгебраический аппарат квантовой информатики 2"
 +
 +
3. М. Н. Аршинов, Л. Е. Садовский — "Коды и математика" (1983)

Текущая версия на 14:07, 1 декабря 2016

Symbol wait.svgЭта работа прошла предварительную проверку
Дата последней правки страницы: 01.12.2016
Данная работа соответствует формальным критериям.
Проверено Sleo.



Построение матрицы Адамара
Последовательный алгоритм
Последовательная сложность [math]O(N^2)[/math]
Объём входных данных [math]1[/math]
Объём выходных данных [math]N^2[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(m)[/math]
Ширина ярусно-параллельной формы [math]4[/math]

Основной автор статьи: Маркова Е.А. 615 гр.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Матрица Адамара [math]H[/math] - это квадратная матрица размера [math]N\times N[/math], составленная из чисел [math]1[/math] и [math]-1[/math], столбцы которой ортогональны, так что справедливо соотношение:

[math]H*H^T = N*E_N[/math],

где [math]E_N[/math] - это единичная матрица размера [math]N[/math]. Матрицы Адамара применяются в различных областях, включая комбинаторику, численный анализ, обработку сигналов.

Предложенный алгоритм является рекурсивным и описывает получение матриц Адамара только порядка степени 2. На каждом следующем шаге алгоритма, новая матрица составляется из матрицы, полученной на предыдущем этапе, путем заполнения соответствующих блоков.

1.2 Математическое описание алгоритма

Пусть [math]H_m[/math] [math]-[/math] матрица Адамара порядка [math]2^m[/math] и [math]-H_m[/math] [math]-[/math] матрица с противоположными элементами. Тогда матрица [math]H_{2m}[/math] получается следующим образом: [math]H_{2m} = \begin{bmatrix} H_m & H_m \\ H_m & -H_m \end{bmatrix} [/math]

Данным алгоритм описывает получение матриц Адамара только порядка степени 2, то есть [math]m[/math] и [math]N[/math] связаны соотношением [math]N = 2^m[/math].

Получение матрицы порядка [math]N[/math] состоит из следующих [math]m[/math] шагов:

Шаг 1: [math]H_1 = (1);[/math]

Шаг 2: [math]H_2 = \begin{pmatrix} 1 & 1 \\1 & -1 \end{pmatrix}; [/math]

Шаг 3: [math]H_3 = \begin{pmatrix} 1 & 1 & 1 & 1 \\1 & -1 & 1 & -1 \\1 & 1 &- 1 & -1 \\1 & -1 & -1 & 1 \end{pmatrix}. [/math]

...

Шаг [math]m[/math]: искомая матрица [math]H_m[/math].

1.3 Вычислительное ядро алгоритма

Вычислительное ядро рекурсивного алгоритма состоит из [math]\;N^2\;[/math] присвоений значений матрицы Адамара

[math]H_{1,1} = 1[/math];

[math]H_{ij} = H_{i(j - \frac{N}{2})}[/math], где [math]i = 1..\frac{N}{2}[/math], [math]j = \frac{N}{2}+1..N[/math];

[math]H_{ij} = H_{(i-\frac{N}{2})j}[/math], где [math]i = \frac{N}{2}+1..N[/math], [math]j = 1.. \frac{N}{2}[/math];

[math]H_{ij} = H_{(i-\frac{N}{2})(j-\frac{N}{2})}[/math], где [math]i = \frac{N}{2}+1..N [/math], [math]j = \frac{N}{2}+1..N[/math].

1.4 Макроструктура алгоритма

Алгоритм не использует в качестве составных частей другие алгоритмы. Как это было описано в вычислительном ядре, в пустые блоки дублируются со сменой или без смены знака значения первого блока матрицы.

1.5 Схема реализации последовательного алгоритма

В описанном виде алгоритм представляет из себя примитивное дублирование элементов матрицы, полученной на предыдущем этапе, в пустующие блоки новой матрицы.

Сначала заполняется правый верхний блок матрицы [math]H[/math]

[math]H_{ij} = H_{i(j - \frac{N}{2})}[/math], где [math]i = 1..\frac{N}{2}[/math], [math]j = \frac{N}{2}+1..N[/math];

затем левый нижний блок

[math]H_{ij} = H_{(i-\frac{N}{2})j}[/math], где [math]i = \frac{N}{2}+1..N[/math], [math]j = 1.. \frac{N}{2}[/math].

Последним заполняется нижний правый блок матрицы

[math]H_{ij} = H_{(i-\frac{N}{2})(j-\frac{N}{2})}[/math], где [math]i = \frac{N}{2}+1..N [/math], [math]j = \frac{N}{2}+1..N[/math].


1.6 Последовательная сложность алгоритма

Для заполнения матрицы [math]H[/math] размера [math]N\times N[/math] необходимо [math]\;N^2\;[/math] присвоений значений. Из чего можно сделать вывод, что рекурсивный метод построения матрицы Адамара является алгоритмом с квадратичной сложностью.

1.7 Информационный граф

Рисунок 1. Граф отображает шаг, стрелками показаны пересылки данных, в узлах происходит операция присвоения значений и инверсия.

1.8 Ресурс параллелизма алгоритма

Логически алгоритм можно разделить на три части, которые на каждом шаге выполняются независимо. Внутри каждой части происходит [math]2^{2N}-2^{2(N-1)}[/math] независимых присвоений, где [math]N[/math] - номер шага алгоритма, причем размерность матрицы на шаге [math]N[/math] равна [math]2^N[/math]. При этом необходимо ждать завершения предыдущего шага, то есть необходимы синхронизирующие блокировки.

1.9 Входные и выходные данные алгоритма

Входные данные: [math]N[/math] - размерность матрицы.

Объем входных данных: 1.

Выходные данные: матрица размером [math]N\times N[/math].

Объем выходных данных: [math] N^2[/math].

1.10 Свойства алгоритма

Вычислительная мощность алгоритма равна суммарному объему входных и выходных данных: [math]N^2 + 1[/math].

Алгоритм полностью детерминирован.

Не смотря на существование недоказанной гипотезы, что существует алгоритм, способный построить матрицы Адамара, размера кратного 4, данный алгоритм вычисляет только матрицы размера степени 2.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование проводилось на кластере ИВМ.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

  • число процессоров [1:32];
  • размер матрицы [32: 16384].

В результате проведённых экспериментов был получен следующий диапазон эффективности алгоритма:

  • минимальная эффективность реализации 0,016%;
  • максимальная эффективность реализации 92%.

На следующих рисунках приведены графики производительности и эффективности выбранной реализации построения Матрицы Адамара в зависимости от изменяемых параметров запуска.

Построим оценки масштабируемости выбранной реализации построения матрицы Адамара:

  • По числу процессоров:
Рисунок 2. Масштабируемость по числу процессоров. По оси ОХ отложено количество процессоров, по оси ОУ - величина производительности для разного размера матрицы.
  • По размеру задачи:
Рисунок 3. Масштабируемость по размеру задачи. По оси ОХ отложена размерность матрицы, по оси ОУ - величина производительности для разного количества процессоров
  • По двум направлениям:
Рисунок 4. Масштабируемость по двум направлениям. По ОХ - количество процессоров, по ОУ - размерность матрицы, по OZ - величина производительности при изменении в двух направлениях.
Рисунок 5. Параллельная реализация построения матрицы Адамара. Изменение производительности в зависимости от числа процессоров и размера матрицы.

Исследованная реализация на языке C

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Реализация MATLAB

Реализация PYTHON

Реализация WOLFRAM

На языке Java реализован класс Hadamard не входящий в стандарт языка. С кодом можно ознакомиться по ссылке.

3 Литература

1. Мак-Вильямс Ф., Слоэн Н. — "Теория кодов, исправляющих ошибки" (1979)

2. Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — "Алгебраический аппарат квантовой информатики 2"

3. М. Н. Аршинов, Л. Е. Садовский — "Коды и математика" (1983)

Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Маркова_Екатерина/Построение_матрицы_Адамара&oldid=19820