Участник:Филимонова Юлия/Решение начальной задачи Коши для системы обыкновенных дифференциальных уравнений методом Рунге-Кутта 4-го порядка: различия между версиями
Jul305a (обсуждение | вклад) |
Jul305a (обсуждение | вклад) |
||
| (не показано 25 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
{{algorithm | {{algorithm | ||
| − | | name = Решение задачи Коши для системы ОДУ методом Рунге- | + | | name = Решение задачи Коши для системы ОДУ методом Рунге-Кутты |
| − | | serial_complexity = | + | | serial_complexity = <math>4 m n</math> |
| − | | pf_height = | + | | pf_height = <math>O(m)</math> |
| − | | pf_width = | + | | pf_width = <math>O(n)</math> |
| − | | input_data = n + 3 | + | | input_data = <math>n + 3</math> |
| − | | output_data = m(n + 1) | + | | output_data = <math>m(n + 1)</math> |
}} | }} | ||
| Строка 14: | Строка 14: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Методы Рунге-Кутты | + | Методы Рунге-Кутты — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой. |
Формально, методом Рунге-Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Классический метод Рунге-Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге-Кутты, опуская порядок. | Формально, методом Рунге-Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Классический метод Рунге-Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге-Кутты, опуская порядок. | ||
| Строка 57: | Строка 57: | ||
Приведем здесь псевдокод | Приведем здесь псевдокод | ||
| + | |||
| + | <source> | ||
начало; | начало; | ||
| − | ввод начальных параметров ( | + | ввод начальных параметров (x[0], t0, t1, m); |
| − | цикл по числу узлов сетки: | + | цикл по числу узлов сетки: i = 1..m-1 |
| − | цикл по числу стадий: | + | цикл по числу стадий: j = 1..4 |
| − | цикл по числу компонент вектора | + | цикл по числу компонент вектора x: k = 1..n |
| − | вычисление коэффициентов | + | вычисление коэффициентов K[j,k,i]; |
| − | конец цикла по | + | конец цикла по k; |
| − | конец цикла по | + | конец цикла по j; |
| − | цикл по числу компонент вектора | + | цикл по числу компонент вектора x: k = 1..n |
| − | вычисление | + | вычисление x[k,i+1]; |
| − | конец цикла по | + | конец цикла по k; |
| − | цикл по числу компонент вектора | + | цикл по числу компонент вектора x: k = 1..n |
| − | сохранение | + | сохранение x[k,i] = x[k,i+1]; |
| − | конец цикла по | + | конец цикла по k; |
| − | вывод | + | вывод x[i+1]; |
| − | конец цикла по | + | конец цикла по n; |
конец; | конец; | ||
| + | |||
| + | </source> | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| − | В данном алгоритме производится четыре операции обращения к функции <math>f</math> (порядка <math>n m</math> арифметических операций) и | + | В данном алгоритме производится четыре операции обращения к функции <math>f</math> (порядка <math>n m</math> арифметических операций) и шестнадцать операций сложения векторов и умножения вектора на число (порядка <math>n</math> арифметических операций). Поскольку операция обращения к функции является более сложной, то сложность последовательного алгоритма можно считать равной <math>4 n m</math>. |
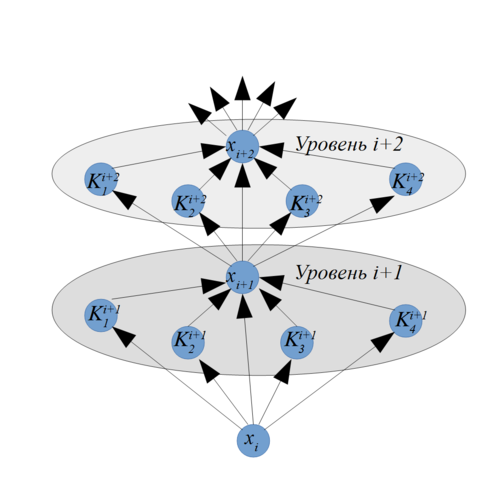
=== Информационный граф === | === Информационный граф === | ||
| + | |||
| + | [[File:Rkg.png|500px|thumb|center|Информационный граф алгоритма]] | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| + | |||
| + | Последовательная схема алгоритма дает основание для организации параллельных вычислений с помощью декомпозиции. Пусть доступно <math>p</math> процессоров (для определенности будем считать, что размерность системы <math>n</math> кратна количество процессоров <math>p</math>: <math>n = qp</math>). На каждый из процессоров распределяется и вычисляется последовательно <math>q</math> компонент векторов коэффициентов. Далее расчеты проводятся следующим образом: | ||
| + | |||
| + | 1. На каждом процессоре вычисляется q соответствующих компонент вектора <math>[K_1]</math> по формуле <math>[K_1] = [f(t_i, x_i)]</math>. Проводится сборка вектора <math>[K_1]</math> целиком на каждом процессоре. | ||
| + | |||
| + | 2-4. Аналогичным образом проводятся вычисления и сборка векторов <math>[K_2], [K_3], [K_4]</math>. | ||
| + | |||
| + | 5. На каждом процессоре вычисляется q соответствующих компонент вектора <math>[x_{i+1}]</math> по формуле <math>[x_{i+1}] = [x_i] + \frac{h}{6} ([K_1] + 2 [K_2] + 2 [K_3] + [K_4])</math>. Проводится сборка вектора <math>[x_{i+1}]</math> целиком на каждом процессоре. Если вычисления не закончены, то сохраняется <math>[x_{i}] = [x_{i+1}]</math>, осуществляется переход на 1. | ||
| + | |||
| + | Алгоритм производит четыре обращения к функции <math>f</math>, шестнадцать операций сложения векторов и умножения вектора на число и четыре операции глобальной сборки векторов. Сложность алгоритма по высоте составляет <math>m</math>, а сложность по ширине равна <math>q = \frac{n}{p}</math>. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| Строка 106: | Строка 122: | ||
# вектор начальных значений <math>x_0</math> размерности <math>n</math>; | # вектор начальных значений <math>x_0</math> размерности <math>n</math>; | ||
# границы временного интервала <math>t_0, t_1</math>; | # границы временного интервала <math>t_0, t_1</math>; | ||
| − | # частота дискретизации <math> | + | # частота дискретизации <math>m</math>. |
Общий размер входных данных <math>n + 3</math>. | Общий размер входных данных <math>n + 3</math>. | ||
| Строка 118: | Строка 134: | ||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| + | |||
| + | Метод Рунге-Кутты 4-го порядка обладает следующими свойствами: | ||
| + | |||
| + | 1. Эти метод (как и все семейство методов Рунге-Кутты) является одношаговым: чтобы найти <math>x_{n+1}</math>, нужна информация об одной предыдущей точке <math>(t_i, x_i)</math>. (Это позволяет в любой момент изменить шаг интегрирования.) | ||
| + | |||
| + | 2. Метод согласуются с рядом Тейлора вплоть до членов порядка <math>4h</math>. (Используя большее количество вспомогательных точек, можно увеличить точность метода.) | ||
| + | |||
| + | 3. Метод не требуют вычисления производных от функции <math>f(t,x)</math>, а только требует вычисления самой функции. | ||
| + | |||
| + | Точность и устойчивость метода достаточна для широкого круга задач, метод прост в реализации - эти достоинства определили популярность метода среди большого количества исследователей. | ||
| + | |||
| + | Число операций алгоритма равно <math>m (n - 1)</math>, общее число входных и выходных данных равно <math>mn + m + n + 3</math>. Следовательно, вычислительная мощность алгоритма | ||
| + | <math>\frac{mn-m}{mn + m + n + 3} \longrightarrow 1</math> при увеличении размерности задачи. | ||
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
| Строка 134: | Строка 163: | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| + | |||
| + | Стандартная схема четвертого порядка реализована в различных математических пакетах: Maple (rkf45), MathCAD (rkfixed), Matlab (ode45). | ||
== Литература == | == Литература == | ||
| + | |||
| + | [1] А. В. Старченко, Высокопроизводительные вычисления на кластерах, Издательство Томского университета, 2013, 127-130 с | ||
| + | |||
| + | [2] Л. П. Фельдман, И. А. Назарова, Параллельные алгоритмы численного решения задачи Коши для систем обыкновенных дифференциальных уравнений | ||
| + | [http://masters.donntu.org/2008/fvti/zavalkin/library/feldman_nazarova2/default.htm] | ||
| + | |||
| + | [3] Е. Е. Тыртышников, Методы численного анализа, М, Академия, 2007 | ||
| + | |||
| + | [4] Ващенко Г.В. Явные методы типа Рунге-Кутты и их параллельные аналоги // Численные методы, программные системы и комплексы программ. | ||
| + | [http://econf.rae.ru/article/5396] | ||
Текущая версия на 18:26, 28 ноября 2016
| Решение задачи Коши для системы ОДУ методом Рунге-Кутты | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]4 m n[/math] |
| Объём входных данных | [math]n + 3[/math] |
| Объём выходных данных | [math]m(n + 1)[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(m)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n)[/math] |
Основные авторы описания: Филимонова Юлия
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Методы Рунге-Кутты — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.
Формально, методом Рунге-Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Классический метод Рунге-Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге-Кутты, опуская порядок.
1.2 Математическое описание алгоритма
Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений размерности [math]n[/math]
[math]\dot{x} = f(t, x),\ t_0 \leqslant t \leqslant t_1,\ x(t_0) = x_0.[/math]
Здесь [math]x(t), x_0 \in \mathbb{R}^n,\ t, t_0, t_1 \in \mathbb{R}, f: \mathbb{R} \rightarrow \mathbb{R}^n[/math].
Введем равномерную сетку
[math]t_i = t_0 + ih,\ i = \overline{1, n},\ h = \frac{t_1 - t_0}{m},[/math]
[math]x(t_i) = x_i.[/math]
Тогда приближенное значение в последующих точках вычисляется по итерационной формуле
[math]x_{i+1} = x_i + \frac{h}{6} (K_1 + 2 K_2 + 2 K_3 + K_4).[/math]
Вычисление нового значения происходит в четыре стадии:
[math]K_1 = f (t_i, x_i),[/math]
[math]K_2 = f (t_i + \frac{h}{2}, x_i + \frac{h}{2} K_1),[/math]
[math]K_3 = f (t_i + \frac{h}{2}, x_i + \frac{h}{2} K_2),[/math]
[math]K_4 = f (t_i + h, x_i + h K_3).[/math]
1.3 Вычислительное ядро алгоритма
В описанной выше вычислительной схеме наиболее трудоемкой является операция обращения к функции [math]f[/math] при вычислении коэффициентов [math]K_i[/math], эта операция является вычислительным ядром.
1.4 Макроструктура алгоритма
Макроструктура алгоритма представлена одним шагом итерационного процесса, описанного в пункте 1.2. Основной макрооперацией алгоритма является операция обращения к функции [math]f[/math], и основное внимание будет уделено распараллеливанию этой операции.
1.5 Схема реализации последовательного алгоритма
Приведем здесь псевдокод
начало;
ввод начальных параметров (x[0], t0, t1, m);
цикл по числу узлов сетки: i = 1..m-1
цикл по числу стадий: j = 1..4
цикл по числу компонент вектора x: k = 1..n
вычисление коэффициентов K[j,k,i];
конец цикла по k;
конец цикла по j;
цикл по числу компонент вектора x: k = 1..n
вычисление x[k,i+1];
конец цикла по k;
цикл по числу компонент вектора x: k = 1..n
сохранение x[k,i] = x[k,i+1];
конец цикла по k;
вывод x[i+1];
конец цикла по n;
конец;1.6 Последовательная сложность алгоритма
В данном алгоритме производится четыре операции обращения к функции [math]f[/math] (порядка [math]n m[/math] арифметических операций) и шестнадцать операций сложения векторов и умножения вектора на число (порядка [math]n[/math] арифметических операций). Поскольку операция обращения к функции является более сложной, то сложность последовательного алгоритма можно считать равной [math]4 n m[/math].
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
Последовательная схема алгоритма дает основание для организации параллельных вычислений с помощью декомпозиции. Пусть доступно [math]p[/math] процессоров (для определенности будем считать, что размерность системы [math]n[/math] кратна количество процессоров [math]p[/math]: [math]n = qp[/math]). На каждый из процессоров распределяется и вычисляется последовательно [math]q[/math] компонент векторов коэффициентов. Далее расчеты проводятся следующим образом:
1. На каждом процессоре вычисляется q соответствующих компонент вектора [math][K_1][/math] по формуле [math][K_1] = [f(t_i, x_i)][/math]. Проводится сборка вектора [math][K_1][/math] целиком на каждом процессоре.
2-4. Аналогичным образом проводятся вычисления и сборка векторов [math][K_2], [K_3], [K_4][/math].
5. На каждом процессоре вычисляется q соответствующих компонент вектора [math][x_{i+1}][/math] по формуле [math][x_{i+1}] = [x_i] + \frac{h}{6} ([K_1] + 2 [K_2] + 2 [K_3] + [K_4])[/math]. Проводится сборка вектора [math][x_{i+1}][/math] целиком на каждом процессоре. Если вычисления не закончены, то сохраняется [math][x_{i}] = [x_{i+1}][/math], осуществляется переход на 1.
Алгоритм производит четыре обращения к функции [math]f[/math], шестнадцать операций сложения векторов и умножения вектора на число и четыре операции глобальной сборки векторов. Сложность алгоритма по высоте составляет [math]m[/math], а сложность по ширине равна [math]q = \frac{n}{p}[/math].
1.9 Входные и выходные данные алгоритма
На вход алгоритма подаются следующие данные:
- вектор начальных значений [math]x_0[/math] размерности [math]n[/math];
- границы временного интервала [math]t_0, t_1[/math];
- частота дискретизации [math]m[/math].
Общий размер входных данных [math]n + 3[/math].
На выходе получаются следующие данные:
- вектор времени [math]t[/math] размерности [math]m[/math];
- матрица значений [math]x[/math] ([math]m[/math] векторов длины [math]n[/math]) размерности [math]m n[/math].
Общий размер выходных данных [math]m + m n[/math].
1.10 Свойства алгоритма
Метод Рунге-Кутты 4-го порядка обладает следующими свойствами:
1. Эти метод (как и все семейство методов Рунге-Кутты) является одношаговым: чтобы найти [math]x_{n+1}[/math], нужна информация об одной предыдущей точке [math](t_i, x_i)[/math]. (Это позволяет в любой момент изменить шаг интегрирования.)
2. Метод согласуются с рядом Тейлора вплоть до членов порядка [math]4h[/math]. (Используя большее количество вспомогательных точек, можно увеличить точность метода.)
3. Метод не требуют вычисления производных от функции [math]f(t,x)[/math], а только требует вычисления самой функции.
Точность и устойчивость метода достаточна для широкого круга задач, метод прост в реализации - эти достоинства определили популярность метода среди большого количества исследователей.
Число операций алгоритма равно [math]m (n - 1)[/math], общее число входных и выходных данных равно [math]mn + m + n + 3[/math]. Следовательно, вычислительная мощность алгоритма [math]\frac{mn-m}{mn + m + n + 3} \longrightarrow 1[/math] при увеличении размерности задачи.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Стандартная схема четвертого порядка реализована в различных математических пакетах: Maple (rkf45), MathCAD (rkfixed), Matlab (ode45).
3 Литература
[1] А. В. Старченко, Высокопроизводительные вычисления на кластерах, Издательство Томского университета, 2013, 127-130 с
[2] Л. П. Фельдман, И. А. Назарова, Параллельные алгоритмы численного решения задачи Коши для систем обыкновенных дифференциальных уравнений [1]
[3] Е. Е. Тыртышников, Методы численного анализа, М, Академия, 2007
[4] Ващенко Г.В. Явные методы типа Рунге-Кутты и их параллельные аналоги // Численные методы, программные системы и комплексы программ. [2]