Участник:Бугаков Юрий/Построение матрицы Адамара произвольной размерности: различия между версиями
| (не показано 50 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Assignment|Sleo}} | ||
| + | Авторы: [[U:Бугаков Юрий|Бугаков Юрий]] (613 группа), Кужамалиев Ернур (601 группа). | ||
| + | |||
| + | Бугаков Юрий: | ||
| + | |||
| + | * Пункты 1.1, 1.2, 1.9, 1.10, 2.1, 2.7; | ||
| + | * Совместное обсуждение и работа над всей статьей в целом с другим автором. | ||
| + | |||
| + | Кужамалиев Ернур: | ||
| + | |||
| + | * Пункты 1.3, 1.4, 1.5, 1.6, 1.7 (рисунки авториские), 1.8; | ||
| + | * Совместное обсуждение и работа над всей статьей в целом с другим автором. | ||
| + | {{algorithm | ||
| + | | name = Построение матрицы Адамара | ||
| + | | serial_complexity = <math>O( \left[ \frac{n}{4}\right]\,2^{2n})</math> | ||
| + | | pf_height = <math>O(1)</math> | ||
| + | | pf_width = <math>O(2^{2n})</math> | ||
| + | | input_data = <math>1</math> | ||
| + | | output_data = <math>2^{2n}</math> | ||
| + | }} | ||
| + | |||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Важную роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века одним из крупнейших французских математиков Жаком Адамаром (1865-1963). | + | Важную роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века одним из крупнейших французских математиков [https://ru.wikipedia.org/wiki/%D0%90%D0%B4%D0%B0%D0%BC%D0%B0%D1%80,_%D0%96%D0%B0%D0%BA Жаком Адамаром (1865-1963)]. Их применение в науке и технике посвящены тысячи публикаций. Они предоставляют эффективные возможности для организации хранения, обработки и передачи информации. |
| − | Квадратная матрица Н порядка | + | Квадратная матрица Н порядка ''m'' с элементами ±1 называется матрицей Адамара, если выполняется условие |
| − | :<math> | + | :<math> H_m\,H_m^T = m\,E_m </math> |
| − | Нетрудно | + | Нетрудно заметить, что различные строки матрицы Адамара попарно ортогональны [1]. Также, можно увидеть из определения, что m четно и |
| + | :<math> | ||
| + | H_{2m} = | ||
| + | \begin{pmatrix} | ||
| + | H_{m} & H_{m}\\ | ||
| + | H_{m} & -H_{m}\end{pmatrix} | ||
| + | </math> | ||
| − | + | С матрицами Адамара связан ряд нерешенных проблем, одна из которых состоит в следующем. Мы уже видели, что порядок ''m'' матрицы Адамара при ''m'' ≥ 3 может быть лишь четным. Более того, при ''m'' ≥ 4 порядок обязан делиться на 4. До сих пор остается открытым вопрос: для любого ли ''m'', кратного 4, существует матрица Адамара порядка m? Неизвестно, в частности, существует ли матрица Адамара порядка 268 (это наименьший порядок, кратный 4, для которого матрица Адамара еще не построена). | |
| − | В | + | Часто матрицу Адамара нормализуют и рассматривают размерности степени 2 (например [2],[3] и [4]). В дальнейшем будем рассматривать только такие случаи. Переопределим матрицу Адамара следующим образом: |
| − | Матрица ''H''<sub>''n''</sub> | + | '''Матрица Адамара ''H''<sub>''n''</sub> - это матрица размера 2<sup>''n''</sup> × 2<sup>''n''</sup>, для которой справедливо равенство''' |
| − | :<math>H_n = H_{1} \otimes H_{n-1}</math> | + | :<math>H_n = H_{1} \otimes H_{n-1}</math>, |
:<math>\begin{align} | :<math>\begin{align} | ||
| Строка 25: | Строка 52: | ||
1 & -1 | 1 & -1 | ||
\end{array}\end{pmatrix} | \end{array}\end{pmatrix} | ||
| − | \end{align}</math> | + | \end{align}</math>, |
| + | '''где <math> \otimes </math> представляет собой [https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BD%D0%B7%D0%BE%D1%80%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5 тензорное произведение].''' | ||
| − | + | Представим некоторые частные примеры матриц Адамара: | |
| − | + | :<math> | |
| + | H_0 = +1, | ||
| + | </math> | ||
| − | + | :<math> | |
| − | : <math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
H_1 = \frac{1}{\sqrt2} | H_1 = \frac{1}{\sqrt2} | ||
| − | + | \begin{pmatrix}\begin{array}{rr} | |
1 & 1\\ | 1 & 1\\ | ||
1 & -1 | 1 & -1 | ||
\end{array}\end{pmatrix} | \end{array}\end{pmatrix} | ||
| − | + | </math>, | |
| − | + | :<math> | |
| − | :<math> | ||
H_2 = \frac{1}{2} | H_2 = \frac{1}{2} | ||
| − | + | \begin{pmatrix}\begin{array}{rrrr} | |
1 & 1 & 1 & 1\\ | 1 & 1 & 1 & 1\\ | ||
1 & -1 & 1 & -1\\ | 1 & -1 & 1 & -1\\ | ||
1 & 1 & -1 & -1\\ | 1 & 1 & -1 & -1\\ | ||
1 & -1 & -1 & 1 | 1 & -1 & -1 & 1 | ||
| − | + | \end{array}\end{pmatrix} | |
| + | </math>, | ||
| + | |||
| + | :<math> | ||
H_3 = \frac{1}{2^{\frac{3}{2}}} | H_3 = \frac{1}{2^{\frac{3}{2}}} | ||
| − | + | \begin{pmatrix}\begin{array}{rrrrrrrr} | |
| − | 1 & 1 & 1 & 1 & | + | 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ |
| − | 1 & -1 & 1 & -1 & | + | 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ |
| − | 1 & 1 & -1 & -1 & | + | 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ |
| − | 1 & -1 & -1 & 1 & | + | 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ |
| − | 1 & 1 & 1 & | + | 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1\\ |
| − | 1 & -1 & 1 & | + | 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1\\ |
| − | 1 & 1 & -1 & | + | 1 & 1 & -1 & 1 & -1 & -1 & 1 & 1\\ |
| − | 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 | + | 1 & -1 & -1 & -1 & -1 & 1 & 1 & -1\\ |
| − | + | \end{array}\end{pmatrix} | |
| − | + | </math>. | |
| − | |||
| − | === | + | === Математическое описание алгоритма === |
| − | + | Основой алгоритма является тот факт, что любую матрицу Адамара <math>H_n</math> размера <math>2^n\times 2^n</math> можно вычислить поэлементно ([3], [4]): | |
| − | |||
| − | ==== | + | :<math>h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}</math>, |
| + | |||
| + | где ''k''<sub>''j''</sub> и ''l''<sub>''j''</sub> коэффициенты двоичного разложения чисел ''k'' и ''l'' (1 или 0): | ||
| + | |||
| + | : <math>k = \sum^{n}_{i=0} {k_i 2^i} = k_{n} 2^{n} + k_{n-1} 2^{n-1} + \cdots + k_1 2 + k_0</math> | ||
| + | |||
| + | и | ||
| + | : <math>l = \sum^{n}_{i=0} {l_i 2^i} = l_{n} 2^{n} + l_{n-1} 2^{n-1} + \cdots + l_1 2 + l_0</math>. | ||
| + | |||
| + | Помимо этой формулы чаще всего используется заполнение по определению. В связи с трудностями распараллеливания и постоянного выделения памяти при каждом шаге рекурсивного вызова этого метода, был выбран предыдущий способ вычисления. | ||
| + | |||
| + | === Вычислительное ядро алгоритма === | ||
| − | + | Вычислительное ядро составляют вычисления элементов матрицы <math>h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}</math>. | |
| − | === | + | === Макроструктура алгоритма === |
| − | + | Основную часть метода составляют вычисления значений степени -1 для каждого элемента: | |
| − | + | : <math>\sum_{j=0}^n k_j l_j</math>. | |
| − | + | Как видно по формуле, получаемое значение равна количеству единиц в двоичной записи результата побитового умножения ''k'' и ''l''. Существует эффективный метод вычисления количества единиц , сложность которого равна ''m'' операций вычитания и ''m'' операций побитового умножения, где ''m''-искомое количество единиц. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === Схема реализации последовательного алгоритма === | |
| − | + | Последовательность исполнения метода следующая: | |
| − | + | 1. Побитовое умножение <math>k\&l</math>; | |
| − | + | 2. Вычисление количества единиц двоичной записи; | |
| − | + | 3. Определение знака элемента по степени. | |
| − | + | === Последовательная сложность алгоритма === | |
| − | + | Для построения матрицы Адамара порядка <math>N=2^n</math> в первом шаге потребуется <math>N^2</math> побитовых умножений ''k&l''. | |
| + | Во втором шаге, как говорилось выше, сложность метода вычисления количества единиц числа в двоичном представлении равна удвоенному количеству единиц. В наихудшем случае сложность равна <math>2log_2N</math>, при ''k=l=N-1'', а в наилучшем 0. Для нахождения степени всех элементов матрицы потребуются <math> 2N^2\left[\frac{log_2N}{4}\right]</math> операций. В третьем шаге для определения знака потребуется <math>N^2</math> операций, то есть сложность алгоритма <math> T(n) = 2\,(1+\left[\frac{n}{4}\right])\,2^{2n}. </math> | ||
| − | + | === Информационный граф === | |
| − | + | На рисунке ниже изображен информационный граф алгоритма. | |
| − | в | + | *<math>k\&l</math> - операция побитового умножения, где <math>k</math> и <math>l</math> соответствующие координаты элемента <math>h_{kl}</math>; |
| + | * OP - вычисление количества единиц числа в двоичной системе. Состоит из последовательного применения операций вычитания и побитового умножения; | ||
| + | * SGN - определение знака соответствующего элемента. Если результат предыдущего шага четное, то знак положительный, иначе отрицательный. | ||
| − | + | [[file:Hadamar.png|thumb|center|1400px|Рисунок 1. Граф алгоритма.]] | |
| + | [[file:OP3.png|thumb|center|1400px|Рисунок 2. Граф OP.]] | ||
| − | === | + | === Ресурс параллелизма алгоритма === |
| − | + | Для построения матрицы порядка <math>N=2^n</math> требуется последовательно выполнить следующие шаги: | |
| + | * <math>N^2</math> вычислений побитового умножения, | ||
| + | * для каждого элемента от <math>2</math> до <math>2n</math> операций вычитания и побитового умножения, в зависимости от результата предыдущего шага, | ||
| + | * <math>N^2</math> для определения знака значения элемента. | ||
| + | |||
| + | Таким образом для построения необходимы лишь простые операции вычитания и побитового умножения выполняемые с целыми положительными числами. Стоит заметить что вычисления для каждого элемента не зависят друг от друга. Также можно воспользоваться либо симметричностью матрицы Адамара либо закономерностью областей показанная в пункте 1.1. | ||
| + | Таким образом, основной вклад в высотe ЯПФ вносит операция вычисления количества единиц. Ширина ЯПФ будет равна <math>O(2^{2n})</math>. | ||
| − | + | === Входные и выходные данные алгоритма === | |
| − | + | '''Входные данные''': натуральное число <math> n \in \N </math> - размерность матрицы Адамара <math>H_n</math>. | |
| − | + | '''Объём входных данных''': 1 (натуральное число <math> n </math>). | |
| − | + | '''Выходные данные''': матрица Адамара <math>H_n</math> размера <math>2^n\times 2^n</math> (элементы <math>h_{ij}</math>). | |
| − | + | '''Объём выходных данных''': <math>2^{2n}</math>, где <math> n </math> - размерность матрицы Адамара. Стоит заметить, что в силу симметричности или самого определения матрицы Адамара, достаточно хранить не все элементы матрицы, а только их часть. | |
| − | + | === Свойства алгоритма === | |
| − | + | * Соотношение последовательной и параллельной сложности: | |
| + | Одним из трудных мест параллельной реализации является правильный выбор количества процессов. Рассматривается некоторое фиксированное число процессов <math>P\in \mathbb{N}</math>. Считается, что каждый процесс ''P'' обрабатывает не более чем <math>\left[\frac{2^{2n}}{P}\right]\geq 1</math> элементов. Тогда качественная формула может быть записана таким образом: <math>T(n,P)=2\,(1+\left[ \frac{n}{4} \right])\,\frac{2^{2n}}{P}</math>. | ||
| − | + | Неравенство <math>\left[\frac{2^{2n}}{P}\right]\geq 1</math> можно переписать, как <math>log_2\,\sqrt{P}\leq n</math>. | |
| − | + | Легко увидеть, что минимум функции ''T(n,P)'' будет при максимально возможном ''P'' : <math>log_2\,\sqrt{P}\leq n</math>. Такое ''P'' будет оптимальным числом процессов для алгоритма. В частности, для <math>P=2^p,\,p\in\mathbb{N}</math> оптимальное <math>P = 2^{2n}</math>. | |
| + | :<math>\frac{T(n)}{T(n,P)}=P</math>. | ||
| + | То есть, отношение последовательной и параллельной сложности будет ''линейно'' зависеть от <math>P</math>; | ||
| − | + | * ''Вычислительная мощность'' алгоритма построения матрицы Адамара, как отношение числа операций к суммарному объему входных и выходных данных: | |
| + | :<math>\,\frac{2^{2n}(2+[\frac{n}{4}])}{1+2^{2n}}\left( \sim [\frac{n}{4}],\,n\to+\infty \right)</math>; | ||
| − | + | * Алгоритм построения матрицы Адамара является ''не детерминированным'', так как число операций меняется в зависимости от входных данных (числа n, которое формирует матрицу размера 2<sup>''n''</sup> × 2<sup>''n''</sup>); | |
| − | + | * Степень исхода вершины информационного графа равна 1; | |
| − | + | * Алгоритм построения матрицы Адамара является ''сбалансированным''. Так как количество вершин на разных процессорах одинаково, то алгоритм является сбалансированным по числу операций на каждом процессоре. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | =ЧАСТЬ Программная реализация алгоритма = | |
| − | |||
| − | |||
| − | + | == Особенности реализации последовательного алгоритма == | |
| − | + | В простейшем варианте генерацию матрицы Адамара для нашего алгоритма можно записать так: | |
| − | + | <source lang="C"> | |
| + | void adamar(int** H, int n) // N = 2^n - размерность матрицы | ||
| + | { | ||
| + | int i,j,N; | ||
| + | float h; | ||
| + | h = pow(1/2,n/2); // h - нормализующий множитель | ||
| + | N = pow(2,n); | ||
| − | + | for(i=0;i<N;++i) | |
| + | { | ||
| + | for(j=0;j<N;++j) | ||
| + | { | ||
| + | ij = i & j; | ||
| + | for (l=0;ij;++l) ij&=ij-1; // l - количество единиц бинарного представления ij | ||
| + | if(l%2==0) H[i][j] = h; | ||
| + | else H[i][j] = -h; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| − | + | Также существует рекурсивная реализация метода построения матрицы Адамара | |
| − | |||
| − | + | <source lang="C"> | |
| − | + | void adamar_recursion(int** H, int N, int i, int j, int h) // h - нормализующий множитель | |
| − | * | + | { |
| − | + | if(n==1) H[i][j] = h; | |
| − | + | else | |
| + | { | ||
| + | adamar(H, N/2, i, j, h); | ||
| + | adamar(H, N/2, i, N/2+j, h); | ||
| + | adamar(H, N/2, N/2+i, j, h); | ||
| + | adamar(H, N/2, N/2+i, N/2+j, -h); | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| − | + | Или эквивалентный безрекурсивный вариант: | |
| − | |||
| − | |||
| − | |||
| − | + | <source lang="C"> | |
| − | + | void adamar_not_recursion(int** H, int n) // N = 2^n - размерность матрицы | |
| − | ** | + | { |
| − | + | int i,j,N; | |
| − | + | float h; | |
| + | h = pow(1/2,n/2); | ||
| + | N = pow(2,n); | ||
| + | k=2; | ||
| + | H[0][0] = h; | ||
| + | |||
| + | while(k<=N) | ||
| + | { | ||
| + | for (i=0; i<k; ++i) | ||
| + | { | ||
| + | for (j=0; j<k; ++j) | ||
| + | { | ||
| + | if (i<k/2 && j<k/2) | ||
| + | { | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | if(i>=k/2 && j>=k/2) | ||
| + | { | ||
| + | H[i][j] = -(H[i-k/2][j-k/2]); | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | if (i>j) | ||
| + | { | ||
| + | H[i][j] = H[i-k/2][j]; | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | H[i][j] = H[i][j-k/2]; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
| + | k=k*2; | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| − | + | Для данного случая, рекурсия является менее эффективной для генерации матрицы Адамара ([https://habrahabr.ru/post/256351/ Хабрахабр. О бедной рекурсии замолвите слово, или всё, что вы не знали и не хотите о ней знать.]). С точки зрения последовательной реализации, генерация матрицы Адамара с помощью adamar_not_recursion будет выигрывать у adamar, так как adamar_not_recursion будет выполнять меньшее количество операций. С точки зрения параллельной реализации adamar имеет 100% парализацию и при определенных условиях будет выигрывать по времени у распараллелинной adamar_not_recursion (пусть в adamar и будет выполняться большее количество операций, но они являются [https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D1%82%D0%BE%D0%B2%D1%8B%D0%B5_%D0%BE%D0%BF%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D0%B8 битовыми операциями]). | |
| − | + | == Локальность данных и вычислений == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Возможные способы и особенности параллельной реализации алгоритма == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Масштабируемость алгоритма и его реализации == | |
| + | Исследование проводилось на суперкомпьютере "Blue Gene". | ||
| − | + | Набор и границы значений изменяемых параметров запуска реализации алгоритма: | |
| − | [ | + | * число процессоров [1, 2, 4, 8,..., 1024] ; |
| − | [ | + | * размер матрицы [2, 4, 8,..., 2048]. |
| − | + | В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма: | |
| − | + | * минимальная эффективность реализации 0.0121%; | |
| − | * | + | * максимальная эффективность реализации 3.3003%. |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | + | На следующих рисунках приведены графики производительности и эффективности выбранной реализации построение матрицы Адамара в зависимости от изменяемых параметров запуска. | |
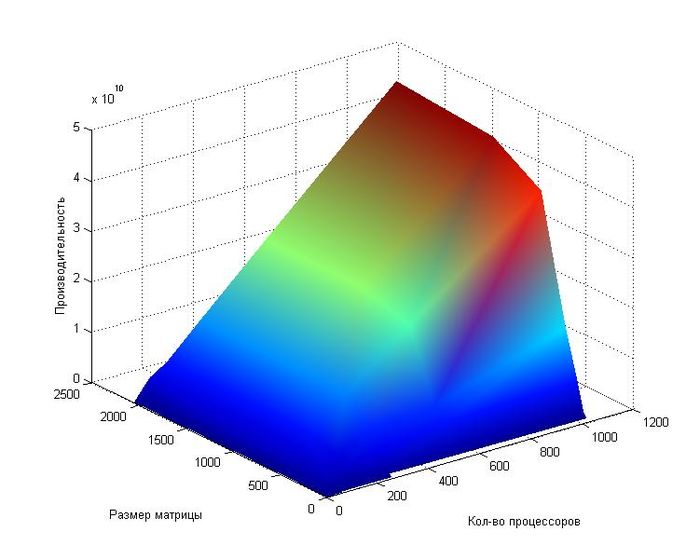
| − | + | [[file:Prois1.jpg|thumb|center|700px|Рис.5 Изменение производительности в зависимости от числа процессоров и размера матрицы.]] | |
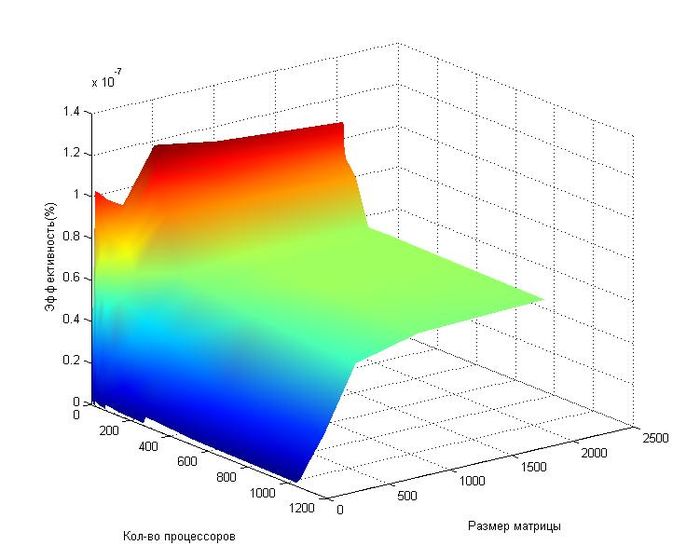
| + | [[file:Effec1.jpg|thumb|center|700px|Рис.5 Изменение эффективности в зависимости от числа процессоров и размера матрицы.]] | ||
| − | = | + | Построим оценки масштабируемости выбранной реализации: |
| + | * При увеличении числа процессов производительность на рассмотренной области изменений параметров запуска увеличивается практически линейно. В следствии этого эффективность реализации, как видно по графику, перестает изменяться при увеличении числа процессоров и равна примерно 1,7%. | ||
| + | * При увеличении размера матрицы производительность на рассмотренной области изменений параметров запуска увеличивается логарифмически. Это связанно с тем, что количество операций зависит от количества единиц после бинарного произведения. Поэтому наиболее влияет порядок степени <math>n</math> размера матрицы <math>N=2^{n}</math>. При увеличении размера матрицы эффективность также увеличивается, но скорость возрастания уменьшается. | ||
| + | По двум направлениям: При рассмотрении увеличения как вычислительной сложности, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности небольшая. | ||
| − | + | == Динамические характеристики и эффективность реализации алгоритма == | |
| − | |||
| − | |||
| − | |||
| − | + | == Выводы для классов архитектур == | |
| − | + | == Существующие реализации алгоритма == | |
| − | + | Примеры вычислительных пакетов, содержащих функции генерации матриц Адамара: | |
| − | + | # [http://www.exponenta.ru/soft/matlab/potemkin/book2/chapter5/hadamard.asp MATLAB]; | |
| + | # [https://reference.wolfram.com/language/ref/HadamardMatrix.html WOLFRAM]; | ||
| + | # [http://pydoc.net/Python/rogues/0.3.0/rogues.matrices.hadamard/ Python]; | ||
| + | # [http://www.obihiro.ac.jp/~suzukim/masuda/octave/html3/octave_97.html Octave]. | ||
| − | + | Стоит отметить, что во многих вычислительных пакетах встроена операция тензорного произведения матриц, которая позволяет строить матрицу Адамара по определению. Этот факт позволяет использовать матрицу Адамара в этих вычислительных пакетах: | |
| + | # [https://ru.wikipedia.org/wiki/Maple MAPLE]; | ||
| + | # [https://ru.wikipedia.org/wiki/Mathcad MATCATH]. | ||
| − | + | = Литература = | |
| + | [1] Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с. | ||
| − | + | [2] Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — Алгебраический аппарат квантовой информатики 2 | |
| − | + | [3] Kunz H.O.. On the Equivalence Between One-Dimensional Discrete Walsh-Hadamard and Multidimensional Discrete Fourier Transforms. IEEE Transactions on Computers. 28 (3): 267–8. [https://en.wikipedia.org/wiki/Digital_object_identifier doi]:[http://ieeexplore.ieee.org/document/1675334/ 10.1109/TC.1979.1675334] | |
| − | + | [4] Википедия – свободная энциклопедия [Электронный ресурс]. - https://en.wikipedia.org/wiki/Hadamard_transform. - (дата обращения: 15.10.2016). | |
| − | [ | + | [5] Воеводин В.В.. Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с. |
| − | |||
| − | |||
| − | |||
| − | + | [6] Воронцов К.В.. Математические методы обучения по прецедентам (теория обучения машин) | |
Текущая версия на 21:50, 20 ноября 2016
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 20.11.2016 Данная работа соответствует формальным критериям. Проверено Sleo. |
Авторы: Бугаков Юрий (613 группа), Кужамалиев Ернур (601 группа).
Бугаков Юрий:
- Пункты 1.1, 1.2, 1.9, 1.10, 2.1, 2.7;
- Совместное обсуждение и работа над всей статьей в целом с другим автором.
Кужамалиев Ернур:
- Пункты 1.3, 1.4, 1.5, 1.6, 1.7 (рисунки авториские), 1.8;
- Совместное обсуждение и работа над всей статьей в целом с другим автором.
| Построение матрицы Адамара | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O( \left[ \frac{n}{4}\right]\,2^{2n})[/math] |
| Объём входных данных | [math]1[/math] |
| Объём выходных данных | [math]2^{2n}[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(1)[/math] |
| Ширина ярусно-параллельной формы | [math]O(2^{2n})[/math] |
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Важную роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века одним из крупнейших французских математиков Жаком Адамаром (1865-1963). Их применение в науке и технике посвящены тысячи публикаций. Они предоставляют эффективные возможности для организации хранения, обработки и передачи информации.
Квадратная матрица Н порядка m с элементами ±1 называется матрицей Адамара, если выполняется условие
- [math] H_m\,H_m^T = m\,E_m [/math]
Нетрудно заметить, что различные строки матрицы Адамара попарно ортогональны [1]. Также, можно увидеть из определения, что m четно и
- [math] H_{2m} = \begin{pmatrix} H_{m} & H_{m}\\ H_{m} & -H_{m}\end{pmatrix} [/math]
С матрицами Адамара связан ряд нерешенных проблем, одна из которых состоит в следующем. Мы уже видели, что порядок m матрицы Адамара при m ≥ 3 может быть лишь четным. Более того, при m ≥ 4 порядок обязан делиться на 4. До сих пор остается открытым вопрос: для любого ли m, кратного 4, существует матрица Адамара порядка m? Неизвестно, в частности, существует ли матрица Адамара порядка 268 (это наименьший порядок, кратный 4, для которого матрица Адамара еще не построена).
Часто матрицу Адамара нормализуют и рассматривают размерности степени 2 (например [2],[3] и [4]). В дальнейшем будем рассматривать только такие случаи. Переопределим матрицу Адамара следующим образом:
Матрица Адамара Hn - это матрица размера 2n × 2n, для которой справедливо равенство
- [math]H_n = H_{1} \otimes H_{n-1}[/math],
- [math]\begin{align} H_1 = \frac{1}{\sqrt2} &\begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \end{align}[/math],
где [math] \otimes [/math] представляет собой тензорное произведение.
Представим некоторые частные примеры матриц Адамара:
- [math] H_0 = +1, [/math]
- [math] H_1 = \frac{1}{\sqrt2} \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} [/math],
- [math] H_2 = \frac{1}{2} \begin{pmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{pmatrix} [/math],
- [math] H_3 = \frac{1}{2^{\frac{3}{2}}} \begin{pmatrix}\begin{array}{rrrrrrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1\\ 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1\\ 1 & 1 & -1 & 1 & -1 & -1 & 1 & 1\\ 1 & -1 & -1 & -1 & -1 & 1 & 1 & -1\\ \end{array}\end{pmatrix} [/math].
1.2 Математическое описание алгоритма
Основой алгоритма является тот факт, что любую матрицу Адамара [math]H_n[/math] размера [math]2^n\times 2^n[/math] можно вычислить поэлементно ([3], [4]):
- [math]h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}[/math],
где kj и lj коэффициенты двоичного разложения чисел k и l (1 или 0):
- [math]k = \sum^{n}_{i=0} {k_i 2^i} = k_{n} 2^{n} + k_{n-1} 2^{n-1} + \cdots + k_1 2 + k_0[/math]
и
- [math]l = \sum^{n}_{i=0} {l_i 2^i} = l_{n} 2^{n} + l_{n-1} 2^{n-1} + \cdots + l_1 2 + l_0[/math].
Помимо этой формулы чаще всего используется заполнение по определению. В связи с трудностями распараллеливания и постоянного выделения памяти при каждом шаге рекурсивного вызова этого метода, был выбран предыдущий способ вычисления.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро составляют вычисления элементов матрицы [math]h_{k,l} = \frac{1}{2^\frac{n}{2}} (-1)^{\sum_j k_j l_j}[/math].
1.4 Макроструктура алгоритма
Основную часть метода составляют вычисления значений степени -1 для каждого элемента:
- [math]\sum_{j=0}^n k_j l_j[/math].
Как видно по формуле, получаемое значение равна количеству единиц в двоичной записи результата побитового умножения k и l. Существует эффективный метод вычисления количества единиц , сложность которого равна m операций вычитания и m операций побитового умножения, где m-искомое количество единиц.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Побитовое умножение [math]k\&l[/math];
2. Вычисление количества единиц двоичной записи;
3. Определение знака элемента по степени.
1.6 Последовательная сложность алгоритма
Для построения матрицы Адамара порядка [math]N=2^n[/math] в первом шаге потребуется [math]N^2[/math] побитовых умножений k&l. Во втором шаге, как говорилось выше, сложность метода вычисления количества единиц числа в двоичном представлении равна удвоенному количеству единиц. В наихудшем случае сложность равна [math]2log_2N[/math], при k=l=N-1, а в наилучшем 0. Для нахождения степени всех элементов матрицы потребуются [math] 2N^2\left[\frac{log_2N}{4}\right][/math] операций. В третьем шаге для определения знака потребуется [math]N^2[/math] операций, то есть сложность алгоритма [math] T(n) = 2\,(1+\left[\frac{n}{4}\right])\,2^{2n}. [/math]
1.7 Информационный граф
На рисунке ниже изображен информационный граф алгоритма.
- [math]k\&l[/math] - операция побитового умножения, где [math]k[/math] и [math]l[/math] соответствующие координаты элемента [math]h_{kl}[/math];
- OP - вычисление количества единиц числа в двоичной системе. Состоит из последовательного применения операций вычитания и побитового умножения;
- SGN - определение знака соответствующего элемента. Если результат предыдущего шага четное, то знак положительный, иначе отрицательный.
1.8 Ресурс параллелизма алгоритма
Для построения матрицы порядка [math]N=2^n[/math] требуется последовательно выполнить следующие шаги:
- [math]N^2[/math] вычислений побитового умножения,
- для каждого элемента от [math]2[/math] до [math]2n[/math] операций вычитания и побитового умножения, в зависимости от результата предыдущего шага,
- [math]N^2[/math] для определения знака значения элемента.
Таким образом для построения необходимы лишь простые операции вычитания и побитового умножения выполняемые с целыми положительными числами. Стоит заметить что вычисления для каждого элемента не зависят друг от друга. Также можно воспользоваться либо симметричностью матрицы Адамара либо закономерностью областей показанная в пункте 1.1. Таким образом, основной вклад в высотe ЯПФ вносит операция вычисления количества единиц. Ширина ЯПФ будет равна [math]O(2^{2n})[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: натуральное число [math] n \in \N [/math] - размерность матрицы Адамара [math]H_n[/math].
Объём входных данных: 1 (натуральное число [math] n [/math]).
Выходные данные: матрица Адамара [math]H_n[/math] размера [math]2^n\times 2^n[/math] (элементы [math]h_{ij}[/math]).
Объём выходных данных: [math]2^{2n}[/math], где [math] n [/math] - размерность матрицы Адамара. Стоит заметить, что в силу симметричности или самого определения матрицы Адамара, достаточно хранить не все элементы матрицы, а только их часть.
1.10 Свойства алгоритма
- Соотношение последовательной и параллельной сложности:
Одним из трудных мест параллельной реализации является правильный выбор количества процессов. Рассматривается некоторое фиксированное число процессов [math]P\in \mathbb{N}[/math]. Считается, что каждый процесс P обрабатывает не более чем [math]\left[\frac{2^{2n}}{P}\right]\geq 1[/math] элементов. Тогда качественная формула может быть записана таким образом: [math]T(n,P)=2\,(1+\left[ \frac{n}{4} \right])\,\frac{2^{2n}}{P}[/math].
Неравенство [math]\left[\frac{2^{2n}}{P}\right]\geq 1[/math] можно переписать, как [math]log_2\,\sqrt{P}\leq n[/math].
Легко увидеть, что минимум функции T(n,P) будет при максимально возможном P : [math]log_2\,\sqrt{P}\leq n[/math]. Такое P будет оптимальным числом процессов для алгоритма. В частности, для [math]P=2^p,\,p\in\mathbb{N}[/math] оптимальное [math]P = 2^{2n}[/math].
- [math]\frac{T(n)}{T(n,P)}=P[/math].
То есть, отношение последовательной и параллельной сложности будет линейно зависеть от [math]P[/math];
- Вычислительная мощность алгоритма построения матрицы Адамара, как отношение числа операций к суммарному объему входных и выходных данных:
- [math]\,\frac{2^{2n}(2+[\frac{n}{4}])}{1+2^{2n}}\left( \sim [\frac{n}{4}],\,n\to+\infty \right)[/math];
- Алгоритм построения матрицы Адамара является не детерминированным, так как число операций меняется в зависимости от входных данных (числа n, которое формирует матрицу размера 2n × 2n);
- Степень исхода вершины информационного графа равна 1;
- Алгоритм построения матрицы Адамара является сбалансированным. Так как количество вершин на разных процессорах одинаково, то алгоритм является сбалансированным по числу операций на каждом процессоре.
2 ЧАСТЬ Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В простейшем варианте генерацию матрицы Адамара для нашего алгоритма можно записать так:
void adamar(int** H, int n) // N = 2^n - размерность матрицы
{
int i,j,N;
float h;
h = pow(1/2,n/2); // h - нормализующий множитель
N = pow(2,n);
for(i=0;i<N;++i)
{
for(j=0;j<N;++j)
{
ij = i & j;
for (l=0;ij;++l) ij&=ij-1; // l - количество единиц бинарного представления ij
if(l%2==0) H[i][j] = h;
else H[i][j] = -h;
}
}
}
Также существует рекурсивная реализация метода построения матрицы Адамара
void adamar_recursion(int** H, int N, int i, int j, int h) // h - нормализующий множитель
{
if(n==1) H[i][j] = h;
else
{
adamar(H, N/2, i, j, h);
adamar(H, N/2, i, N/2+j, h);
adamar(H, N/2, N/2+i, j, h);
adamar(H, N/2, N/2+i, N/2+j, -h);
}
}
Или эквивалентный безрекурсивный вариант:
void adamar_not_recursion(int** H, int n) // N = 2^n - размерность матрицы
{
int i,j,N;
float h;
h = pow(1/2,n/2);
N = pow(2,n);
k=2;
H[0][0] = h;
while(k<=N)
{
for (i=0; i<k; ++i)
{
for (j=0; j<k; ++j)
{
if (i<k/2 && j<k/2)
{
}
else
{
if(i>=k/2 && j>=k/2)
{
H[i][j] = -(H[i-k/2][j-k/2]);
}
else
{
if (i>j)
{
H[i][j] = H[i-k/2][j];
}
else
{
H[i][j] = H[i][j-k/2];
}
}
}
}
}
k=k*2;
}
}
Для данного случая, рекурсия является менее эффективной для генерации матрицы Адамара (Хабрахабр. О бедной рекурсии замолвите слово, или всё, что вы не знали и не хотите о ней знать.). С точки зрения последовательной реализации, генерация матрицы Адамара с помощью adamar_not_recursion будет выигрывать у adamar, так как adamar_not_recursion будет выполнять меньшее количество операций. С точки зрения параллельной реализации adamar имеет 100% парализацию и при определенных условиях будет выигрывать по времени у распараллелинной adamar_not_recursion (пусть в adamar и будет выполняться большее количество операций, но они являются битовыми операциями).
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование проводилось на суперкомпьютере "Blue Gene".
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [1, 2, 4, 8,..., 1024] ;
- размер матрицы [2, 4, 8,..., 2048].
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 0.0121%;
- максимальная эффективность реализации 3.3003%.
На следующих рисунках приведены графики производительности и эффективности выбранной реализации построение матрицы Адамара в зависимости от изменяемых параметров запуска.
Построим оценки масштабируемости выбранной реализации:
- При увеличении числа процессов производительность на рассмотренной области изменений параметров запуска увеличивается практически линейно. В следствии этого эффективность реализации, как видно по графику, перестает изменяться при увеличении числа процессоров и равна примерно 1,7%.
- При увеличении размера матрицы производительность на рассмотренной области изменений параметров запуска увеличивается логарифмически. Это связанно с тем, что количество операций зависит от количества единиц после бинарного произведения. Поэтому наиболее влияет порядок степени [math]n[/math] размера матрицы [math]N=2^{n}[/math]. При увеличении размера матрицы эффективность также увеличивается, но скорость возрастания уменьшается.
По двум направлениям: При рассмотрении увеличения как вычислительной сложности, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности небольшая.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Примеры вычислительных пакетов, содержащих функции генерации матриц Адамара:
Стоит отметить, что во многих вычислительных пакетах встроена операция тензорного произведения матриц, которая позволяет строить матрицу Адамара по определению. Этот факт позволяет использовать матрицу Адамара в этих вычислительных пакетах:
3 Литература
[1] Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с.
[2] Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — Алгебраический аппарат квантовой информатики 2
[3] Kunz H.O.. On the Equivalence Between One-Dimensional Discrete Walsh-Hadamard and Multidimensional Discrete Fourier Transforms. IEEE Transactions on Computers. 28 (3): 267–8. doi:10.1109/TC.1979.1675334
[4] Википедия – свободная энциклопедия [Электронный ресурс]. - https://en.wikipedia.org/wiki/Hadamard_transform. - (дата обращения: 15.10.2016).
[5] Воеводин В.В.. Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.
[6] Воронцов К.В.. Математические методы обучения по прецедентам (теория обучения машин)