Уровень алгоритма

Участник:Артем Таран/Графо-ориентированный алгоритм кластеризации CHAMELEON: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
 
(не показано 109 промежуточных версий 3 участников)
Строка 1: Строка 1:
 +
{{Assignment|Algoman|Kronberg}}
 +
 
{{algorithm
 
{{algorithm
 
| name              = Графо-ориентированный алгоритм кластеризации CHAMELEON
 
| name              = Графо-ориентированный алгоритм кластеризации CHAMELEON
 
| serial_complexity = <math>O(n^2+nm+m^2log(m))</math>
 
| serial_complexity = <math>O(n^2+nm+m^2log(m))</math>
−
| pf_height        = <math></math>
+
| pf_height        = <math>O(n + log(n) + mlog(m) + m^2log(m))</math>
−
| pf_width          = <math></math>
+
| pf_width          = <math>O(n)</math>
 
| input_data        = <math>\frac{n (n - 1)}{2}</math>
 
| input_data        = <math>\frac{n (n - 1)}{2}</math>
 
| output_data      = <math>n</math>
 
| output_data      = <math>n</math>
 
}}
 
}}
  
−
Статью подготовили: [[Участник:Артем_Таран|Артём Таран Иванович]], [[Участник:ShimchikN|Шимчик Никита Владимирович]].
+
Статью подготовили: [[Участник:Артем_Таран|Артём Таран Иванович]] (разделы 1.1 - 1.10, 2.7), [[Участник:ShimchikN|Шимчик Никита Владимирович]] (разделы 1.1 - 1.10, 2.7).
 
== Свойства и структура алгоритма ==
 
== Свойства и структура алгоритма ==
  
Строка 15: Строка 17:
 
Кластеризация — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры) с минимизацией межкластерного сходства и максимизацией внутрикластерного сходства.
 
Кластеризация — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры) с минимизацией межкластерного сходства и максимизацией внутрикластерного сходства.
  
−
Графо-ориентированный алгоритм кластеризации CHAMELEON достаточно новый алгоритм, который измеряет сходство двух кластеров на основе
+
Графо-ориентированный алгоритм кластеризации CHAMELEON<ref name="rt">http://www-users.cs.umn.edu/~han/dmclass/chameleon.pdf</ref> - алгоритм, который измеряет сходство двух кластеров на основе
 
динамической модели. В процессе кластеризации два кластера объединяются, только если показатели взаимосвязанности и близости между двумя кластерами являются высокими по отношению к показателям внутренней взаимосвязанности кластеров и близости элементов внутри этих кластеров. Процесс слияния с использованием динамической модели, использующийся в данном алгоритме облегчает открытие
 
динамической модели. В процессе кластеризации два кластера объединяются, только если показатели взаимосвязанности и близости между двумя кластерами являются высокими по отношению к показателям внутренней взаимосвязанности кластеров и близости элементов внутри этих кластеров. Процесс слияния с использованием динамической модели, использующийся в данном алгоритме облегчает открытие
 
природных и однородных кластеров. Методология динамического моделирования кластеров, использующаяся в CHAMELEON,
 
природных и однородных кластеров. Методология динамического моделирования кластеров, использующаяся в CHAMELEON,
 
применима ко всем типам данных, для которых может быть построена матрица подобия.
 
применима ко всем типам данных, для которых может быть построена матрица подобия.
 +
 +
Следует отметить, что конечное число кластеров не задаётся явным образом и зависит как от выбора параметров алгоритма, так и от внутренней структуры входных данных.
  
 
Алгоритм кластеризации CHAMELEON включает в себя три этапа:
 
Алгоритм кластеризации CHAMELEON включает в себя три этапа:
Строка 27: Строка 31:
  
 
3) Формирование набора кластеров, на основе множества подграфов, полученных на предыдущем этапе.
 
3) Формирование набора кластеров, на основе множества подграфов, полученных на предыдущем этапе.
 +
 +
[[Файл:Графы k ближайших соседей.jpg|1000px|thumb|center|Графы k ближайших соседей: 1) объекты в пространстве, 2) граф по принципу 1-го ближайшего соседа, 3) граф по принципу 2-го ближайшего соседа, 4) граф по принципу 3-х ближайших соседей<ref name="rt">http://www-users.cs.umn.edu/~han/dmclass/chameleon.pdf</ref>]]
  
 
=== Математическое описание алгоритма ===
 
=== Математическое описание алгоритма ===
−
Исходные данные: треугольная матрица <math>A</math> (элементы <math>a_{ij}</math>).
+
==== Данные ====
 +
* '''Исходные данные''': множество из <math>n</math> точек <math>V = \{v_{i}\}</math> в метрическом пространстве, которое может быть задано в виде треугольной матрицы расстояний <math>A</math> размера <math>n\times n</math>; натуральное число <math>k</math>, используемое в качестве параметра алгоритма поиска k ближайших соседей.
 +
 
 +
* '''Промежуточный результат после первого этапа''': граф <math>G = (V, E)</math>, полученный путём соединения каждой точки с её <math>k</math> ближайшими соседями.
 +
 
 +
* '''Промежуточный результат после второго этапа''': разбиение множества <math>V</math> на набор <math>K = \{K_{i}\}</math> попарно непересекающихся связных подмножеств, из которого образуется взвешенный граф <math>G_{2} = (K, E_{2})</math>.
 +
 
 +
* '''Промежуточный результат после третьего этапа''': итоговое разбиение множества вершин графа <math>G_{2}</math> на набор кластеров <math>C = \{C_{i}\}</math>.
 +
 
 +
* '''Вычисляемые данные''': n-мерный вектор <math>v</math> (элементы <math>v_{i}</math>), показывающий отображение исходного множества точек на набор кластеров <math>C</math>.
 +
 
 +
==== Определения ====
 +
 
 +
* ''Абсолютная взаимная связность между парой кластеров <math>C_{i}</math> и <math>C_{j}</math>'' определяется как сумма весов ребер, соединяющих вершины, принадлежащие <math>C_{i}</math> с вершинами из <math>C_{j}</math>. Эти ребра, фактически, входят в разделитель ребер графа, состоящего из кластеров <math>C_{i}</math> и <math>C_{j}</math>, и разбивающим его на подграфы <math>C_{i}</math> и <math>C_{j}</math>. Обозначается эта величина как
 +
<math>EC_{(C_{i},C_{j})}</math>. Внутреннюю связность <math>EC_{C_{i}}</math> кластера <math>C_{i}</math> можно вычислить как сумму ребер, входящих в разделитель ребер, разбивающий <math>C_{i}</math> на два совершенно равных подграфа.
 +
 
 +
* ''Относительная взаимная <math>RI_{(C_{i},C_{j})}</math> связность  пары кластеров <math>C_{i}</math> и <math>C_{j}</math>'' определяется формулой:
 +
 
 +
<math>RI_{(C_{i},C_{j})} = \frac{2*|EC_{(C_{i},C_{j})}|}{|EC_{C_{i}}|+|EC_{C_{j}}|}</math>
 +
 
 +
Учитывая значения относительной взаимной связности, можно добиться получения кластеров разного размера, формы и плотности, то есть общего внутреннего сходства.
 +
 
 +
* ''Абсолютное взаимное сходство между парой кластеров <math>C_{i}</math> и <math>C_{j}</math>'' подсчитывается как среднее сходство между соединенными вершинами, принадлежащими <math>C_{i}</math> и <math>C_{j}</math> соответственно. Эти соединения обусловлены предыдущим разбиением общего графа, полученного на матрице сходства.
 +
 
 +
* ''Относительное взаимное сходство <math>RC_{(C_{i},C_{j})}</math> между парой кластеров <math>C_{i}</math> и <math>C_{j}</math>'' определяется как абсолютное сходство между этой парой кластеров, нормализованное с учетом их внутреннего сходства и вычисляется по формуле:
 +
 
 +
<math> RC_{(C_{i},C_{j})}= \frac{S_{EC_{(C_{i},C_{j})}}}{\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{i})}}+\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{j})}}}</math>,
 +
 
 +
где <math>S_{EC_{(C_{i})}}</math> и <math>S_{EC_{(C_{i})}}</math> - средние веса ребер (значения сходства), принадлежащих разделителю ребер кластеров <math>C_{i}</math> и <math>C_{j}</math> соответственно,
 +
и <math>S_{EC_{(C_{i},C_{j})}}</math> - средний вес ребер, соединяющих вершины <math>C_{i}</math> с вершинами <math>C_{j}</math>, причем ребра принадлежат разделителю ребер <math>EC_{(C_{i})}</math>, определенному ранее.
 +
 
 +
Далее, алгоритм применяет агломеративную иерархическую кластеризацию с использованием вышеозначенных показателей. Причем существует две стратегии их учета. Первая подразумевает наличие некоторых пороговых значений <math>T_{RI}</math> и <math>T_{RC}</math>. В соответствии с этой стратегией, алгоритм для каждого кластера <math>C_{i}</math> проверяет, отвечают ли смежные (наиболее близкие) ему кластеры условиям:
 +
 
 +
*<math>RI_{(C_{i},C_{j})} \geqslant T_{RI}</math>
  
−
Вычисляемые данные: n-мерный вектор <math>v</math> (элементы <math>v_{i}</math>).
+
*<math>RC_{(C_{i},C_{j})} \geqslant T_{RC}</math>
  
 +
Если более одного смежного кластера отвечает этим условиям, то алгоритм выбирает для объединения наиболее связный кластер (граф), то есть такой кластер <math>C_{j}</math>, с которым у кластера <math>C_{i}</math> получается наибольшая абсолютная взаимная связность. По завершению прохода по всем кластерам, созданные таким образом пары объединяются. Параметры <math>T_{RI}</math> и <math>T_{RC}</math> могут использоваться для изменения характеристик получаемых кластеров.
  
−
Формулы метода:
+
Вторая стратегия заключается в использовании специальной функции, объединяющей понятия относительной взаимной связности и относительного взаимного сходства. На каждом шаге выбираются те кластеры для объединения, которые максимизируют эту функцию:
−
:<math>
 
−
\begin{align}
 
−
l_{11} & = \sqrt{a_{11}}, \\
 
−
l_{j1} & = \frac{a_{j1}}{l_{11}}, \quad j \in [2, n], \\
 
−
l_{ii} & = \sqrt{a_{ii} - \sum_{p = 1}^{i - 1} l_{ip}^2}, \quad i \in [2, n], \\
 
−
l_{ji} & = \left (a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp} \right ) / l_{ii}, \quad i \in [2, n - 1], j \in [i + 1, n].
 
−
\end{align}
 
−
</math>
 
  
−
Существует также блочная версия метода, однако в данном описании разобран только точечный метод.
+
<math>RI_{(C_{i},C_{j})}*RC_{(C_{i},C_{j})}^\alpha</math>,
  
−
В ряде реализаций деление на диагональный элемент выполняется в два этапа: вычисление <math>\frac{1}{l_{ii}}</math> и затем умножение на него всех (видоизменённых) <math>a_{ji}</math> . Здесь мы этот вариант алгоритма не рассматриваем. Заметим только, что он имеет худшие параллельные характеристики, чем представленный.
+
где <math>\alpha</math> выбирается пользователем. Если <math>\alpha > 1 </math>, то алгоритм придает большее значение относительному взаимному сходству, а если <math>\alpha <  1 </math>, то большее значение имеет относительная взаимная связность. Разумеется, данный подход позволяет получить полную дендрограмму кластерного анализа<ref name="rty">http://studopedia.ru/7_41934_algoritm-dinamicheskoy-ierarhicheskoy-klasterizatsii-CHAMELEON.html</ref>.
  
 
=== Вычислительное ядро алгоритма ===
 
=== Вычислительное ядро алгоритма ===
 +
 +
На первом этапе работы алгоритма вычислительным ядром можно считать процесс нахождения k ближайших соседей для каждой отдельной вершины.
 +
 +
На втором этапе работы алгоритма вычислительным ядром является поиск разбиения графа на два подграфа с минимизацией разделителя рёбер графа.
 +
 +
На третьем этапе работы алгоритма вычислительным ядром является расчёт <math>EC_{(C_{i},C_{j})}</math>, <math>RC_{(C_{i},C_{j})}</math> и <math>RI_{(C_{i},C_{j})}</math> для пары смежных кластеров, а также их слияние.
  
 
=== Макроструктура алгоритма ===
 
=== Макроструктура алгоритма ===
 +
 +
Алгоритм CHAMELEON выполняется в 3 этапа, последовательных относительно друг друга. Каждый этап соответствует отдельному алгоритму.
 +
 +
* Макрооперацией на первом этапе является процедура выделения k ближайших соседей.
 +
 +
* Макрооперацией на втором этапе является процедура разбиения наибольшего подграфа на каждой итерации.
 +
 +
* Макрооперациями на третьем этапе являются процедуры вычисления метрики для принятия решения об объединении кластеров и объединение кластеров на каждой итерации.
 +
 
=== Схема реализации последовательного алгоритма ===
 
=== Схема реализации последовательного алгоритма ===
 +
 +
* Первый этап (псевдокод):
 +
  integer n; // Количество точек.
 +
  integer k; // Параметр k
 +
  integer A[n][n]; // Верхняя треугольная матрица расстояний между точками.
 +
 
 +
  integer E[n][n]; // Верхняя треугольная матрица рёбер графа G - изначально инициализирована нулями.
 +
  foreach (integer i in (1,n-1) ) {
 +
    integer Neighbours[k]; // матрица, используемая хранения ближайших соседей
 +
    integer countN = 0;
 +
   
 +
    foreach (integer j in (i+1, n) ) {
 +
      // Заполняем матрицу Neighbours, добавляя новые элементы и увеличивая счётчик countN.
 +
      // Когда countN станет равен k, новые элементы будут вставляться на место старых, либо отбрасываться.
 +
    }
 +
 
 +
    foreach (integer j in (0, countN) ) {
 +
      E[min(i,j), max(i,j)] = 1;
 +
    }
 +
  }
 +
  return E;
 +
 +
* Второй этап:
 +
  [[File:Диаграмма_шаг_2.png]]
 +
 +
* Третий этап:
 +
  [[File:Chameleon_stage_3.png|611px]]
  
 
=== Последовательная сложность алгоритма ===
 
=== Последовательная сложность алгоритма ===
Строка 63: Строка 137:
  
 
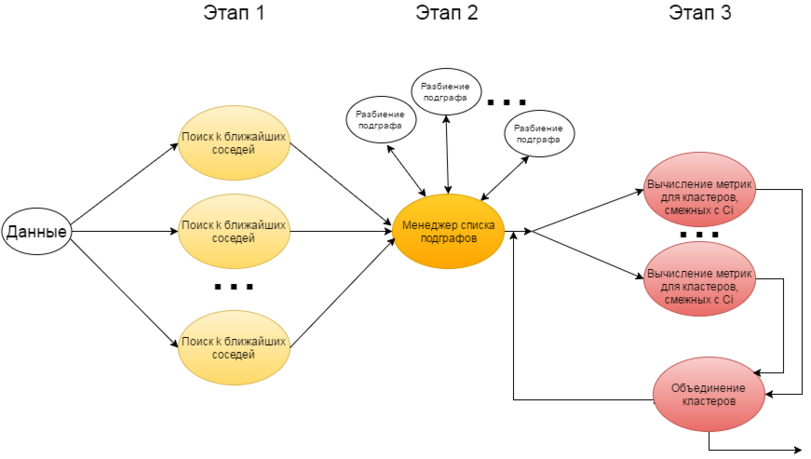
=== Информационный граф ===
 
=== Информационный граф ===
 +
 +
  [[File:Chameleon_inforgraph.png|811px]]
  
 
=== Ресурс параллелизма алгоритма ===
 
=== Ресурс параллелизма алгоритма ===
  
−
=== Входные и выходные данные алгоритма ===
+
Первый этап работы алгоритма можно распределить между <math>n</math> процессами: в этом случае каждому процессу назначается своя точка и происходит поиск <math>k</math> ближайших соседей. Таким образом, его параллельная сложность составляет <math>O(n)</math>.
  
−
* Входные данные: треугольная матрица <math>A</math> размерности <math>n*n</math> (где n — количество объектов), в которой элементу <math>a_{ij}</math> соответствует расстояние между i-м и j-м объектами.
+
На втором этапе количество задействованных процессов может варьироваться в зависимости от входных данных. В худшем случае число итераций можно оценить как <math>O(log(n))</math>.
  
−
* Объём входных данных: <math>n</math>
+
На третьем этапе можно распараллелить процесс расчёта метрик сходства между кластерами, однако итоговое слияние всё равно должно выполняться последовательно.
 +
Поскольку процесс сравнения кластеров возможно распараллелить, сложность 3-го этапа составляет <math>mlog(m) + m^2log(m)</math>.
  
−
* Выходные данные: n-мерный вектор <math>v</math>, в котором элементу <math>v_{i}</math> соответствует номер кластера, присвоенный i-му объекту
+
Таким образом, суммарная параллельная сложность оказывается равна <math>O(n + log(n) + mlog(m) + m^2log(m))</math>.
  
−
* Объём выходных данных: <math>\frac{n (n - 1)}{2}</math>
+
=== Входные и выходные данные алгоритма ===
  
−
=== Свойства алгоритма ===
+
* Входные данные:
  
−
== Программная реализация алгоритма ==
+
1) Треугольная матрица <math>A</math> размера <math>n\times n</math> (где n — количество объектов), в которой элементу <math>a_{ij}</math> соответствует расстояние между i-м и j-м объектами.
−
== Литература ==
 
  
−
Данный алгоритм выполняется в два этапа.
+
2) Количество ближайших соседей <math>k</math> для вершин (рекомендуемое значение <math>k</math> от 5 до 20 в зависимости от количества анализируемых объектов).
  
−
На первом этапе CHAMELEON использует алгоритм разделения графа для получения набора относительно малых кластеров. На втором этапе, для объединения кластеров, полученных на первом этапе, в настоящие кластеры, используется иерархическая агломеративная кластеризация. Таким образом, алгоритм, фактически, является гибридным, построенным комбинацией графо-ориентированных и классических иерархических методов. Рассмотрим эти этапы подробнее.
+
3) Наименьшее число вершин, которое может содержать наибольший подграф на 2-м этапе <math>l</math>. Величина этого параметра варьируется от 1 до 5 % от общего числа объектов.
  
−
На первом этапе, согласно графо-ориентированному подходу, происходит построение графа на матрице сходства объектов по принципу k ближайших соседей. Две вершины такого графа соединяет ребро, если объект, соответствующий любой из этих вершин попадает в число k наиболее близких объектов для объекта, соответствующего другой вершине из данной пары.
+
* Объём входных данных: <math>\frac{n (n - 1)}{2}</math>
−
[[Файл:Графы k ближайших соседей.jpg|2000px|thumb|left|На рисунке изображены: 1) объекты в пространстве, 2) граф по принципу 1-го ближайшего соседа, 3) граф по принципу 2-го ближайшего соседа, 4)граф по принципу 3-х ближайших соседей]]
 
  
−
Такое представление имеет целый ряд преимуществ.
+
* Выходные данные: n-мерный вектор <math>v</math>, в котором элементу <math>v_{i}</math> соответствует номер кластера, присвоенный i-му объекту
  
−
Во-первых, можно сразу убрать ребра в графе с достаточно малым весом (значением сходства).
+
* Объём выходных данных: <math>n</math>
  
−
Во-вторых, возможно динамически определить для различных участков графа количество k ближайших соседей для вершин, на основе плотности данных отдельно взятого участка, которую, в свою очередь, можно определить на основе весов ребер.
+
=== Свойства алгоритма ===
  
−
В-третьих, операции на графах (например, разделение графа), имеющих такое представление, выполняются гораздо быстрее, чем на полных графах.
+
Первый этап алгоритма обладает хорошим ресурсом параллелизма: параллельная сложность его выполнения составляет <math>O(n)</math>, что намного лучше последовательной оценки <math>O(n^2)</math>.
  
−
Обычно, k берется в пределах от 5 до 20 в зависимости от количества анализируемых объектов, и, как свидетельствуют авторы, выбор k почти не оказывает влияния на результаты кластеризации.
+
У второго и третьего этапов алгоритма сложно полностью оценить ресурсы параллелизма. Но оба этапа возможно частично распараллелить.
  
−
Далее, алгоритм разделяет полученный граф на множество сравнительно малых подграфов. Разделение происходит последовательно. На каждом шаге выбирается под-граф, содержащий наибольшее число вершин. Этот граф разделяется на два подграфа, так, что разделитель ребер графа минимален и каждый из получаемых подграфов содержит не менее 25 % вершин исходного графа. Процесс разделения останавливается, когда наибольший под-граф содержит меньше некоторого заданного числа вершин. Обычно величина этого параметра задается равной значению от 1 до 5 % от числа объектов. Полученное множество связных графов считается множеством начальных кластеров, на котором требуется провести последовательное иерархическое объединение.
+
'''Вычислительную мощность''' для разных этапов алгоритма можно оценить как:
  
−
На втором этапе, алгоритм последовательно объединяет кластеры, используя значение их относительной взаимной связности и относительного взаимного сходства. Только если оба эти значения достаточно высоки у двух кластеров, они объединяются.
+
1 этап: <math>O(1)</math>
  
−
Относительная взаимная связность пары кластеров определяется абсолютной взаимной связностью кластеров, нормализованной с учетом внутренней связности (п. 0) каждого кластера (подграфа). Нормализация используется для того, чтобы исключить тенденцию к преимущественному объединению крупных кластеров, у которых, определенно, значение взаимной связности будет больше, вследствие их размера.
+
2 этап: <math>O(\frac{nm}{n^2+m^2})</math>
  
−
Абсолютная взаимная связность между парой кластеров Ci и Сj определяется как сумма весов ребер, соединяющих вершины, принадлежащие Ci с вершинами из Сj. Эти ребра, фактически, входят в разделитель ребер графа, состоящего из кластеров Ci и Сj, и разбивающим его на подграфы Ci и Сj. Обозначается эта величина как  . Внутреннюю связность  кластера Ci можно вычислить как сумму ребер, входящих в разделитель ребер, разбивающий Ci на два совершенно равных подграфа.
+
3 этап: <math>O(\frac{m^2log(m)}{m^2+n})</math>
 +
 +
<b>Детерминированность:</b> Важной особенностью данного алгоритма является его недетерминированность. Несмотря на то, что 1-й этап детерминирован, алгоритм в целом является недетерминированным, так как на 2-ом этапе могут быть найдены различные разбиения на подграфы, а это повлияет и на итоговый результат работы алгоритма.
  
−
Относительная взаимная связность  пары кластеров Ci и Сj определяется формулой:
+
== Программная реализация алгоритма ==
  
 +
=== Особенности реализации последовательного алгоритма ===
  
 +
=== Локальность данных и вычислений ===
  
−
Учитывая значения относительной взаимной связности, можно добиться получения кластеров разного размера, формы и плотности, то есть общего внутреннего сходства.
+
=== Возможные способы и особенности параллельной реализации алгоритма ===
  
−
Относительное взаимное сходство пары кластеров определяется как абсолютное сходство между этой парой кластеров, нормализованное с учетом их внутреннего сходства.
+
=== Масштабируемость алгоритма и его реализации ===
  
−
Абсолютное взаимное сходство между парой кластеров Ci и Сj подсчитывается как среднее сходство между соединенными вершинами, принадлежащими Ci и Сj соответственно. Эти соединения обусловлены предыдущим (на первом этапе) разбиением общего графа, полученного на матрице сходства.
+
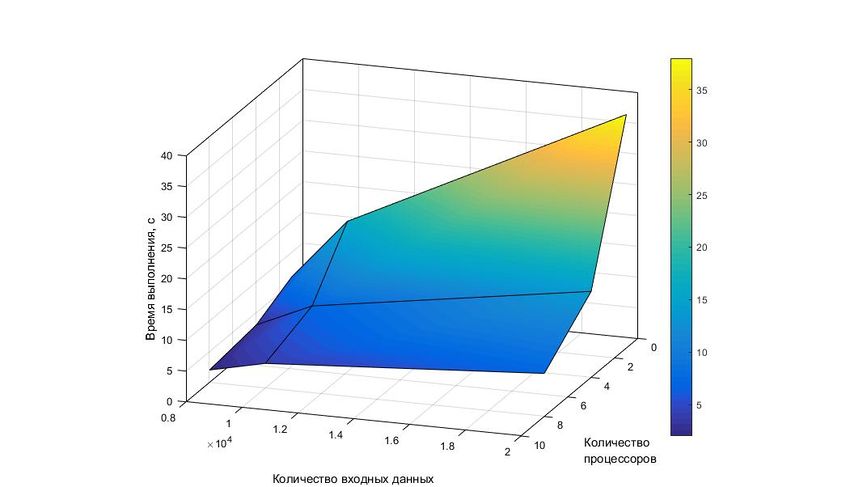
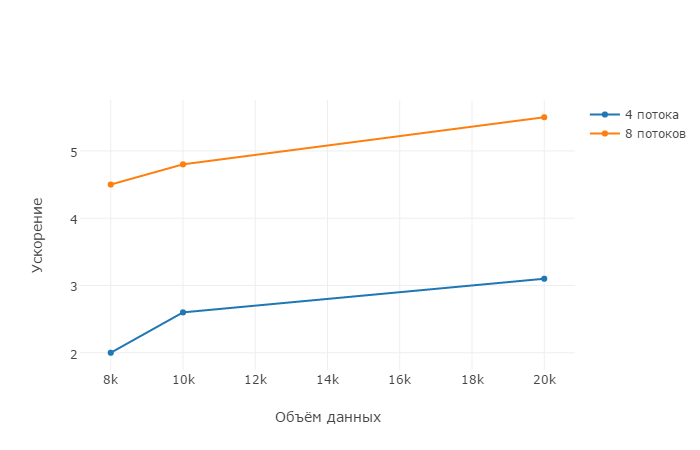
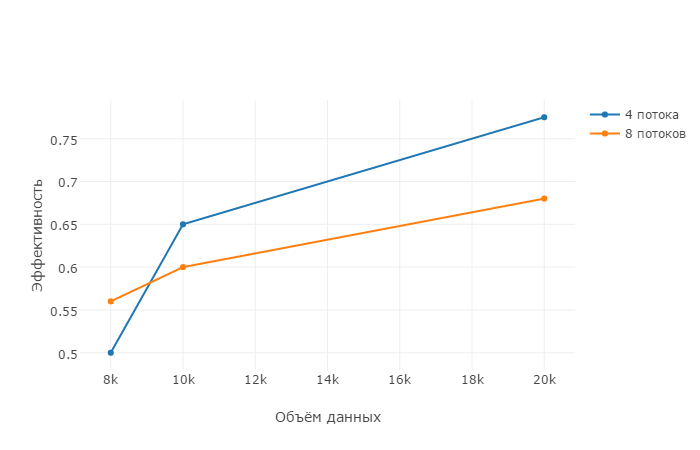
Проводилось исследование масштабируемости экспериментальной версии параллельной реализации алгоритма для малого числа потоков<ref name="tr">http://research.ijcaonline.org/volume79/number8/pxc3891600.pdf</ref>.
  
−
Итак, относительное взаимное сходство  между парой кластеров Ci и Сj равно:
+
Его результаты отражены на графиках. Из графиков видно, что ускорение и эффективность алгоритма растут с увеличением объема данных.
  
 +
Однако можно заметить, что с увеличением числа потоков эффективность алгоритма падает.
  
 +
  [[File:Plot cham.jpg|850px|center]]
 +
 +
[[File:Cham_speedup.png]] [[File:Cham_eff.png]]
  
−
где  и – средние веса ребер (значения сходства), принадлежащих разделителю ребер кластеров Ci и Сj соответственно, и  – средний вес ребер, соединяющих вершины Ci с вершинами Сj, причем ребра принадлежат разделителю ребер  , определенному ранее. Можно также подсчитать внутреннее сходство как среднее значение весов всех связей в кластере, однако использования разделителя ребер по мнению авторов метода предпочтительнее. Этот факт они связывают с тем, что связи между объектами, помещенными в один кластер на ранних этапах объединения, сильнее, чем на поздних.
+
=== Динамические характеристики и эффективность реализации алгоритма ===
  
−
Далее, алгоритм применяет агломеративную иерархическую кластеризацию с использованием вышеозначенных показателей. Причем существует две стратегии их учета. Первая подразумевает наличие некоторых пороговых значений. T­RI и T­RC. В соответствии с этой стратегией, алгоритм для каждого кластера Ci проверяет, отвечают ли смежные (наиболее близкие) ему кластеры условиям:
+
=== Выводы для классов архитектур ===
  
 +
=== Существующие реализации алгоритма ===
  
 +
Существует несколько последовательных реализаций алгоритма. С одной из них можно ознакомиться по ссылке <ref name="tra">http://www.codeforge.com/article/192925</ref>.
  
−
Если более одного смежного кластера отвечает этим условиям, то алгоритм выбирает для объединения наиболее связный кластер (граф), то есть такой кластер Сj, с которым у кластера Ci получается наибольшая абсолютная взаимная связность. По завершению прохода по всем кластерам, созданные таким образом пары объединяются. Параметры T­RI и T­RC могут использоваться для изменения характеристик получаемых кластеров.
+
Возможна реализация алгоритма CHAMELEON с использованием графовых библиотек, как, например METIS <ref name="tru">http://glaros.dtc.umn.edu/gkhome/metis/metis/overview</ref> , hMETIS <ref name="tri">http://glaros.dtc.umn.edu/gkhome/metis/hmetis/overview</ref> и RANN <ref name="tro">https://cran.r-project.org/web/packages/RANN/index.html</ref>.
  
−
Таким образом, основное отличие данного подхода от классических агломеративных иерархических методов в том, что, во-первых, на каждом шаге могут быть объединены несколько кластеров, а, во-вторых, на каком-то этапе ни одна пара кластеров не будет удовлетворять вышеуказанным условиям и такое разбиение будет считаться оптимальным, то есть в конце может не получиться один всеохватывающий кластер. Если данное разбиение не удовлетворяет выбранным критериям, то пороговые значения можно уменьшить.
+
Параллельных реализаций алгоритма CHAMELEON найдено не было. Однако существует исследование, связанное с реализацией CHAMELEON посредством технологии OpenMP, с которым можно ознакомиться здесь <ref name="tr">http://research.ijcaonline.org/volume79/number8/pxc3891600.pdf</ref>.
  
−
Вторая стратегия заключается в использовании специальной функции, объединяющей понятия относительной взаимной связности и относительного взаимного сходства. На каждом шаге выбираются те кластеры для объединения, которые максимизируют эту функцию:
+
== Литература ==
−
 
 
−
 
 
−
 
 
−
где a выбирается пользователем. Если a > 1, то алгоритм придает большее значение относительному взаимному сходству, а если a < 1, то большее значение имеет относительная взаимная связность. Разумеется, данный подход позволяет получить полную дендрограмму кластерного анализа.
 
  
−
Общая временная сложность этого алгоритма выражается как  , где n – количество анализируемых документов, m­ – количество получившихся после первого этапа малых кластеров.
+
<references \>

Текущая версия на 17:31, 29 ноября 2016

Symbol confirmed.svgЭта работа успешно выполнена
Преподавателю: в основное пространство, в подстраницу
Данное задание было проверено и зачтено.
Проверено Kronberg и Algoman.



Графо-ориентированный алгоритм кластеризации CHAMELEON
Последовательный алгоритм
Последовательная сложность [math]O(n^2+nm+m^2log(m))[/math]
Объём входных данных [math]\frac{n (n - 1)}{2}[/math]
Объём выходных данных [math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(n + log(n) + mlog(m) + m^2log(m))[/math]
Ширина ярусно-параллельной формы [math]O(n)[/math]


Статью подготовили: Артём Таран Иванович (разделы 1.1 - 1.10, 2.7), Шимчик Никита Владимирович (разделы 1.1 - 1.10, 2.7).

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Кластеризация — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры) с минимизацией межкластерного сходства и максимизацией внутрикластерного сходства.

Графо-ориентированный алгоритм кластеризации CHAMELEON[1] - алгоритм, который измеряет сходство двух кластеров на основе динамической модели. В процессе кластеризации два кластера объединяются, только если показатели взаимосвязанности и близости между двумя кластерами являются высокими по отношению к показателям внутренней взаимосвязанности кластеров и близости элементов внутри этих кластеров. Процесс слияния с использованием динамической модели, использующийся в данном алгоритме облегчает открытие природных и однородных кластеров. Методология динамического моделирования кластеров, использующаяся в CHAMELEON, применима ко всем типам данных, для которых может быть построена матрица подобия.

Следует отметить, что конечное число кластеров не задаётся явным образом и зависит как от выбора параметров алгоритма, так и от внутренней структуры входных данных.

Алгоритм кластеризации CHAMELEON включает в себя три этапа:

1) Построение графа, путём добавления рёбер по принципу k ближайших соседей.

2) Выделение множества сравнительно малых связных подграфов.

3) Формирование набора кластеров, на основе множества подграфов, полученных на предыдущем этапе.

Графы k ближайших соседей: 1) объекты в пространстве, 2) граф по принципу 1-го ближайшего соседа, 3) граф по принципу 2-го ближайшего соседа, 4) граф по принципу 3-х ближайших соседей[1]

1.2 Математическое описание алгоритма

1.2.1 Данные

  • Исходные данные: множество из [math]n[/math] точек [math]V = \{v_{i}\}[/math] в метрическом пространстве, которое может быть задано в виде треугольной матрицы расстояний [math]A[/math] размера [math]n\times n[/math]; натуральное число [math]k[/math], используемое в качестве параметра алгоритма поиска k ближайших соседей.
  • Промежуточный результат после первого этапа: граф [math]G = (V, E)[/math], полученный путём соединения каждой точки с её [math]k[/math] ближайшими соседями.
  • Промежуточный результат после второго этапа: разбиение множества [math]V[/math] на набор [math]K = \{K_{i}\}[/math] попарно непересекающихся связных подмножеств, из которого образуется взвешенный граф [math]G_{2} = (K, E_{2})[/math].
  • Промежуточный результат после третьего этапа: итоговое разбиение множества вершин графа [math]G_{2}[/math] на набор кластеров [math]C = \{C_{i}\}[/math].
  • Вычисляемые данные: n-мерный вектор [math]v[/math] (элементы [math]v_{i}[/math]), показывающий отображение исходного множества точек на набор кластеров [math]C[/math].

1.2.2 Определения

  • Абсолютная взаимная связность между парой кластеров [math]C_{i}[/math] и [math]C_{j}[/math] определяется как сумма весов ребер, соединяющих вершины, принадлежащие [math]C_{i}[/math] с вершинами из [math]C_{j}[/math]. Эти ребра, фактически, входят в разделитель ребер графа, состоящего из кластеров [math]C_{i}[/math] и [math]C_{j}[/math], и разбивающим его на подграфы [math]C_{i}[/math] и [math]C_{j}[/math]. Обозначается эта величина как

[math]EC_{(C_{i},C_{j})}[/math]. Внутреннюю связность [math]EC_{C_{i}}[/math] кластера [math]C_{i}[/math] можно вычислить как сумму ребер, входящих в разделитель ребер, разбивающий [math]C_{i}[/math] на два совершенно равных подграфа.

  • Относительная взаимная [math]RI_{(C_{i},C_{j})}[/math] связность пары кластеров [math]C_{i}[/math] и [math]C_{j}[/math] определяется формулой:

[math]RI_{(C_{i},C_{j})} = \frac{2*|EC_{(C_{i},C_{j})}|}{|EC_{C_{i}}|+|EC_{C_{j}}|}[/math]

Учитывая значения относительной взаимной связности, можно добиться получения кластеров разного размера, формы и плотности, то есть общего внутреннего сходства.

  • Абсолютное взаимное сходство между парой кластеров [math]C_{i}[/math] и [math]C_{j}[/math] подсчитывается как среднее сходство между соединенными вершинами, принадлежащими [math]C_{i}[/math] и [math]C_{j}[/math] соответственно. Эти соединения обусловлены предыдущим разбиением общего графа, полученного на матрице сходства.
  • Относительное взаимное сходство [math]RC_{(C_{i},C_{j})}[/math] между парой кластеров [math]C_{i}[/math] и [math]C_{j}[/math] определяется как абсолютное сходство между этой парой кластеров, нормализованное с учетом их внутреннего сходства и вычисляется по формуле:

[math] RC_{(C_{i},C_{j})}= \frac{S_{EC_{(C_{i},C_{j})}}}{\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{i})}}+\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{j})}}}[/math],

где [math]S_{EC_{(C_{i})}}[/math] и [math]S_{EC_{(C_{i})}}[/math] - средние веса ребер (значения сходства), принадлежащих разделителю ребер кластеров [math]C_{i}[/math] и [math]C_{j}[/math] соответственно, и [math]S_{EC_{(C_{i},C_{j})}}[/math] - средний вес ребер, соединяющих вершины [math]C_{i}[/math] с вершинами [math]C_{j}[/math], причем ребра принадлежат разделителю ребер [math]EC_{(C_{i})}[/math], определенному ранее.

Далее, алгоритм применяет агломеративную иерархическую кластеризацию с использованием вышеозначенных показателей. Причем существует две стратегии их учета. Первая подразумевает наличие некоторых пороговых значений [math]T_{RI}[/math] и [math]T_{RC}[/math]. В соответствии с этой стратегией, алгоритм для каждого кластера [math]C_{i}[/math] проверяет, отвечают ли смежные (наиболее близкие) ему кластеры условиям:

  • [math]RI_{(C_{i},C_{j})} \geqslant T_{RI}[/math]
  • [math]RC_{(C_{i},C_{j})} \geqslant T_{RC}[/math]

Если более одного смежного кластера отвечает этим условиям, то алгоритм выбирает для объединения наиболее связный кластер (граф), то есть такой кластер [math]C_{j}[/math], с которым у кластера [math]C_{i}[/math] получается наибольшая абсолютная взаимная связность. По завершению прохода по всем кластерам, созданные таким образом пары объединяются. Параметры [math]T_{RI}[/math] и [math]T_{RC}[/math] могут использоваться для изменения характеристик получаемых кластеров.

Вторая стратегия заключается в использовании специальной функции, объединяющей понятия относительной взаимной связности и относительного взаимного сходства. На каждом шаге выбираются те кластеры для объединения, которые максимизируют эту функцию:

[math]RI_{(C_{i},C_{j})}*RC_{(C_{i},C_{j})}^\alpha[/math],

где [math]\alpha[/math] выбирается пользователем. Если [math]\alpha \gt 1 [/math], то алгоритм придает большее значение относительному взаимному сходству, а если [math]\alpha \lt 1 [/math], то большее значение имеет относительная взаимная связность. Разумеется, данный подход позволяет получить полную дендрограмму кластерного анализа[2].

1.3 Вычислительное ядро алгоритма

На первом этапе работы алгоритма вычислительным ядром можно считать процесс нахождения k ближайших соседей для каждой отдельной вершины.

На втором этапе работы алгоритма вычислительным ядром является поиск разбиения графа на два подграфа с минимизацией разделителя рёбер графа.

На третьем этапе работы алгоритма вычислительным ядром является расчёт [math]EC_{(C_{i},C_{j})}[/math], [math]RC_{(C_{i},C_{j})}[/math] и [math]RI_{(C_{i},C_{j})}[/math] для пары смежных кластеров, а также их слияние.

1.4 Макроструктура алгоритма

Алгоритм CHAMELEON выполняется в 3 этапа, последовательных относительно друг друга. Каждый этап соответствует отдельному алгоритму.

  • Макрооперацией на первом этапе является процедура выделения k ближайших соседей.
  • Макрооперацией на втором этапе является процедура разбиения наибольшего подграфа на каждой итерации.
  • Макрооперациями на третьем этапе являются процедуры вычисления метрики для принятия решения об объединении кластеров и объединение кластеров на каждой итерации.

1.5 Схема реализации последовательного алгоритма

  • Первый этап (псевдокод):
 integer n; // Количество точек.
 integer k; // Параметр k
 integer A[n][n]; // Верхняя треугольная матрица расстояний между точками.
 
 integer E[n][n]; // Верхняя треугольная матрица рёбер графа G - изначально инициализирована нулями.
 foreach (integer i in (1,n-1) ) {
   integer Neighbours[k]; // матрица, используемая хранения ближайших соседей
   integer countN = 0;
   
   foreach (integer j in (i+1, n) ) {
     // Заполняем матрицу Neighbours, добавляя новые элементы и увеличивая счётчик countN.
     // Когда countN станет равен k, новые элементы будут вставляться на место старых, либо отбрасываться.
   }
 
   foreach (integer j in (0, countN) ) {
     E[min(i,j), max(i,j)] = 1;
   }
 }
 return E;
  • Второй этап:
 Диаграмма шаг 2.png
  • Третий этап:
 Chameleon stage 3.png

1.6 Последовательная сложность алгоритма

1) Построение графа на основе метода k ближайших соседей в худшем случае требует [math]O(n^2)[/math] операций;

2) Для выделения множества сравнительно малых связных подграфов требуется [math]nm[/math] операций;

3) Формирование набора кластеров, на основе множества подграфов, полученных на предыдущем этапе, требует [math]m^2log(m)[/math] операций.

Итого, получаем последовательную сложность [math]O(n^2+nm+m^2log(m))[/math].

1.7 Информационный граф

 Chameleon inforgraph.png

1.8 Ресурс параллелизма алгоритма

Первый этап работы алгоритма можно распределить между [math]n[/math] процессами: в этом случае каждому процессу назначается своя точка и происходит поиск [math]k[/math] ближайших соседей. Таким образом, его параллельная сложность составляет [math]O(n)[/math].

На втором этапе количество задействованных процессов может варьироваться в зависимости от входных данных. В худшем случае число итераций можно оценить как [math]O(log(n))[/math].

На третьем этапе можно распараллелить процесс расчёта метрик сходства между кластерами, однако итоговое слияние всё равно должно выполняться последовательно. Поскольку процесс сравнения кластеров возможно распараллелить, сложность 3-го этапа составляет [math]mlog(m) + m^2log(m)[/math].

Таким образом, суммарная параллельная сложность оказывается равна [math]O(n + log(n) + mlog(m) + m^2log(m))[/math].

1.9 Входные и выходные данные алгоритма

  • Входные данные:

1) Треугольная матрица [math]A[/math] размера [math]n\times n[/math] (где n — количество объектов), в которой элементу [math]a_{ij}[/math] соответствует расстояние между i-м и j-м объектами.

2) Количество ближайших соседей [math]k[/math] для вершин (рекомендуемое значение [math]k[/math] от 5 до 20 в зависимости от количества анализируемых объектов).

3) Наименьшее число вершин, которое может содержать наибольший подграф на 2-м этапе [math]l[/math]. Величина этого параметра варьируется от 1 до 5 % от общего числа объектов.

  • Объём входных данных: [math]\frac{n (n - 1)}{2}[/math]
  • Выходные данные: n-мерный вектор [math]v[/math], в котором элементу [math]v_{i}[/math] соответствует номер кластера, присвоенный i-му объекту
  • Объём выходных данных: [math]n[/math]

1.10 Свойства алгоритма

Первый этап алгоритма обладает хорошим ресурсом параллелизма: параллельная сложность его выполнения составляет [math]O(n)[/math], что намного лучше последовательной оценки [math]O(n^2)[/math].

У второго и третьего этапов алгоритма сложно полностью оценить ресурсы параллелизма. Но оба этапа возможно частично распараллелить.

Вычислительную мощность для разных этапов алгоритма можно оценить как:

1 этап: [math]O(1)[/math]

2 этап: [math]O(\frac{nm}{n^2+m^2})[/math]

3 этап: [math]O(\frac{m^2log(m)}{m^2+n})[/math]

Детерминированность: Важной особенностью данного алгоритма является его недетерминированность. Несмотря на то, что 1-й этап детерминирован, алгоритм в целом является недетерминированным, так как на 2-ом этапе могут быть найдены различные разбиения на подграфы, а это повлияет и на итоговый результат работы алгоритма.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Проводилось исследование масштабируемости экспериментальной версии параллельной реализации алгоритма для малого числа потоков[3].

Его результаты отражены на графиках. Из графиков видно, что ускорение и эффективность алгоритма растут с увеличением объема данных.

Однако можно заметить, что с увеличением числа потоков эффективность алгоритма падает.

Plot cham.jpg
Cham speedup.png Cham eff.png

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Существует несколько последовательных реализаций алгоритма. С одной из них можно ознакомиться по ссылке [4].

Возможна реализация алгоритма CHAMELEON с использованием графовых библиотек, как, например METIS [5] , hMETIS [6] и RANN [7].

Параллельных реализаций алгоритма CHAMELEON найдено не было. Однако существует исследование, связанное с реализацией CHAMELEON посредством технологии OpenMP, с которым можно ознакомиться здесь [3].

3 Литература

<references \>

  1. ↑ 1,0 1,1 http://www-users.cs.umn.edu/~han/dmclass/chameleon.pdf
  2. ↑ http://studopedia.ru/7_41934_algoritm-dinamicheskoy-ierarhicheskoy-klasterizatsii-CHAMELEON.html
  3. ↑ 3,0 3,1 http://research.ijcaonline.org/volume79/number8/pxc3891600.pdf
  4. ↑ http://www.codeforge.com/article/192925
  5. ↑ http://glaros.dtc.umn.edu/gkhome/metis/metis/overview
  6. ↑ http://glaros.dtc.umn.edu/gkhome/metis/hmetis/overview
  7. ↑ https://cran.r-project.org/web/packages/RANN/index.html
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Артем_Таран/Графо-ориентированный_алгоритм_кластеризации_CHAMELEON&oldid=19481