Участник:Emaksimov/Кластеризация сетями Кохонена: различия между версиями
Emaksimov (обсуждение | вклад) |
Teplov (обсуждение | вклад) |
||
| (не показано 112 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Assignment | Teplov}} | |
| − | [[ | + | |
| + | {{algorithm | ||
| + | | name = Кластеризация сетями Кохонена | ||
| + | | serial_complexity = <math>O(mnT)</math> | ||
| + | | input_data = <math>mk</math> | ||
| + | | output_data = <math>mn</math> | ||
| + | | pf_height = <math>O(T*log(max(m,n)))</math> | ||
| + | | pf_width = <math>O(mn)</math> | ||
| + | }} | ||
| + | |||
| + | Авторы страницы <b>[[Участник:Emaksimov|Егор Максимов]] (1.1, 1.2, 1.4, 1.5, 1.6, 1.7, 1.9, 2.4, 1.10)</b> и <b>[[Участник:Kravtsovkirill|Кирилл Кравцов]] (1.2, 1.3, 1.6, 1.7, 1.8, 1.9, 1.10, 2.4, 2.7)</b> | ||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
| Строка 6: | Строка 16: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
'''Искусственная нейронная сеть Кохонена''' или самоорганизующаяся карта признаков (SOM) была предложена финским исследователем Тойво Кохоненом в начале 1980-х годов. | '''Искусственная нейронная сеть Кохонена''' или самоорганизующаяся карта признаков (SOM) была предложена финским исследователем Тойво Кохоненом в начале 1980-х годов. | ||
| − | [[Файл:Teuvokohonen.jpg|thumb|150px|right| | + | [[Файл:Teuvokohonen.jpg|thumb|150px|right|Рис. 1. Кохонен, Теуво.]] |
| − | Она представляет собой двухслойную сеть. Каждый нейрон первого (распределительного) слоя соединен со всеми нейронами второго (выходного) слоя, которые расположены в виде двумерной решетки. Нейроны выходного слоя называются кластерными элементами, их количество определят максимальное количество групп, на которые система может разделить входные данные. Увеличивая количество нейронов второго слоя можно увеличивать детализацию результатов процесса кластеризации. | + | Она представляет собой двухслойную сеть. Каждый нейрон первого (распределительного) слоя соединен со всеми нейронами второго (выходного) слоя, которые расположены в виде двумерной решетки. Для визуализации топологии слоя Кохонена используют либо шестиугольные, либо прямоугольные ячейки, в которых распологаются нейроны. Шестиугольные ячейки часто являются более предпочтительными, так как расстояние от центра выбранной ячейки до ее соседей одинаково.Нейроны выходного слоя называются кластерными элементами, их количество определят максимальное количество групп, на которые система может разделить входные данные. Увеличивая количество нейронов второго слоя можно увеличивать детализацию результатов процесса кластеризации. |
Система работает по принципу соревнования – нейроны второго слоя соревнуются друг с другом за право наилучшим образом сочетаться с входным вектором сигналов, побеждает тот элемент-нейрон, чей вектор весов ближе всего к входному вектору сигналов. За меру близости двух векторов можно взять квадрат евклидова расстояния. Таким образом, каждый входной вектор относится к некоторому кластерному элементу. | Система работает по принципу соревнования – нейроны второго слоя соревнуются друг с другом за право наилучшим образом сочетаться с входным вектором сигналов, побеждает тот элемент-нейрон, чей вектор весов ближе всего к входному вектору сигналов. За меру близости двух векторов можно взять квадрат евклидова расстояния. Таким образом, каждый входной вектор относится к некоторому кластерному элементу. | ||
| Строка 16: | Строка 26: | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| + | [[Файл:FNaEm.png|thumb|550px|right|Риc. 2. Кластеризация сетями Кохонена]] | ||
Пусть имеется некоторое множество векторов <math> x^{(i)}=(x_1^{(i)},x_2^{(i)},...,x_m^{(i)}) \in \mathbb{R}^m, i=1, \dots, k</math>. Заранее зададим количество кластеров равным <math>n</math>. Соответственно, Карта Кохонена представляет собой двухслойную fully-connected нейронную сеть, где первый слой состоит из <math>m</math> нейронов, а второй - из <math>n</math>. | Пусть имеется некоторое множество векторов <math> x^{(i)}=(x_1^{(i)},x_2^{(i)},...,x_m^{(i)}) \in \mathbb{R}^m, i=1, \dots, k</math>. Заранее зададим количество кластеров равным <math>n</math>. Соответственно, Карта Кохонена представляет собой двухслойную fully-connected нейронную сеть, где первый слой состоит из <math>m</math> нейронов, а второй - из <math>n</math>. | ||
Каждый j-ый нейрон описывается вектором весов <math> w_j=(w_{1j},w_{2j},...,w_{mj}), j=1, \dots, n</math>. | Каждый j-ый нейрон описывается вектором весов <math> w_j=(w_{1j},w_{2j},...,w_{mj}), j=1, \dots, n</math>. | ||
| − | + | ==== Алгоритм обучения сети без учителя==== | |
Обучение состоит из последовательности коррекций векторов, представляющих собой нейроны. Сначала следует инициализировать векторы весов. Далее определенное количество раз (эпох) производятся следующие действия: | Обучение состоит из последовательности коррекций векторов, представляющих собой нейроны. Сначала следует инициализировать векторы весов. Далее определенное количество раз (эпох) производятся следующие действия: | ||
| − | + | #Случайным образов выбирается вектор <math>x(t)</math> из входных данных. | |
| − | # Случайным образов выбирается вектор <math>x(t)</math> из входных данных. | + | #Выбирается нейрон-победитель <math>w_c</math> "наиболее похожий" (по евклидову расстоянию) на вектор <math>x(t)</math>: <center> <math> ||x(t)-w_c||=\min\limits_{i}(||x(t)-w_i(t)||)</math>. </center> |
| − | + | # Веса всех нейронов обновляются по формуле: | |
| − | # Выбирается нейрон-победитель <math>w_c</math> "наиболее похожий" (по евклидову расстоянию) на вектор <math>x(t)</math>: | + | <center> <math> w_i(t+1)=w_i(t)+\alpha(t)h_{ic}(t)||x(t)-w_i(t)||</math>, </center> |
| − | + | где <math>t</math> - номер эпохи, <math> h_{ic}(t)</math>- функция соседства нейронов, | |
| − | # Веса всех нейронов обновляются по формуле: <math> w_i(t+1)=w_i(t)+\alpha(t)h_{ic}(t)||x(t)-w_i(t)||</math>, где | ||
| − | <math>t</math> - номер эпохи, <math> h_{ic}(t)</math>- функция соседства нейронов, | ||
<math>\alpha (t)</math> - функция скорости обучения сети. | <math>\alpha (t)</math> - функция скорости обучения сети. | ||
| − | + | ==== Инициализация начальных весов==== | |
| − | |||
Инициализация случайными значениями, когда всем весам даются малые случайные величины. | Инициализация случайными значениями, когда всем весам даются малые случайные величины. | ||
| − | Инициализация примерами, когда в качестве начальных значений задаются значения случайно выбранных примеров из обучающей выборки. | + | Инициализация примерами, когда в качестве начальных значений задаются значения случайно выбранных примеров из обучающей выборки |
| + | Линейная инициализация. В этом случае веса инициируются значениями векторов, линейно упорядоченных вдоль линейного подпространства, проходящего между двумя главных собственными векторами исходного набора данных. Собственные вектора могут быть найдены например при помощи процедуры Грама-Шмидта. | ||
| − | + | ==== Функция соседства нейронов==== | |
Функции от расстояния применяются двух видов: | Функции от расстояния применяются двух видов: | ||
| − | Константа: <math> | + | Константа: |
| − | h(d,t) = \begin{cases} | + | <math> |
| − | + | h(d,t) = \begin{cases} | |
| − | + | c, & \mbox{if } n \ d<=\delta \\ | |
| − | \end{cases}</math> | + | 0, & \mbox{if } n \ d>\delta |
| + | \end{cases}</math> | ||
| − | |||
| − | |||
| − | + | Функция Гаусса: | |
| − | + | <math>h_{ic}(t)=\exp(-\frac{\|r_c-r_i\|^2}{2\sigma^2(t)})</math>, | |
| − | <math> | + | где <math>r_i</math> определяет положение <math>i</math>-го нейрона в сетке |
| − | |||
| − | + | ==== Функция скорости обучения сети==== | |
| − | + | Главное требование к ней - монотонное убывание при возрастании <math>t</math> для замедления темпов вариации весов нейронов слоя Кохонена. | |
| + | Функция может быть задана, например, как <math>\alpha(t)=\frac{A}{B+t}</math>, где <math>A</math> и <math>B</math> - некоторые константы. | ||
| − | + | === Вычислительное ядро алгоритма === | |
| − | + | Вычислительное ядро алгоритма состоит из двух шагов, повторяющихся каждую итерацию (эпоху): | |
| + | *Вычисление расстояния от случайно выбранного вектора <math>x(t)</math> до каждого нейрона и выбор нейрона с наименьшим расстоянием. Т.е. вычисление <math>n</math> евклидовых расстояний и сортировка полученного массива расстояний. Сложность евклидового расстояния растет линейно с увеличением длины вектора. Следовательно получаем сложность данного шага <math>O(mn)</math>. | ||
| + | *Обновление весов всех нейронов. Пусть используется гауссовская функция для вычисления расстояний между нейронами. Сложность обновления веса одного нейрона линейно зависит от <math>m</math>. Т.е. сложность данного шага также <math>O(mn)</math>. | ||
| − | + | В итоге получаем, что для всего алгоритма с количеством эпох равным <math>T</math> сложность составляет <math>O(Tmn)</math>. | |
| − | |||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| + | Алгоритм кластеризации можно разбить на следующие этапы: | ||
| + | *Инициализация <math>\mathbf{W} \leftarrow ComputeInitialWeights(\mathbf{W})</math> | ||
| − | <math>\mathbf{ | + | *Цикл, повторяющийся <math>T_{max}</math> (максимальное число "эпох") раз: |
| + | # <math>\mathbf{X} \leftarrow ChooseRandomVector(\mathbf{V})</math> | ||
| + | #Вложенный цикл, в котором осуществляется вычисление расстояний <math>\mathbf{D_i} \leftarrow CalculateEucledeNorm(X, \mathbf{W_i})</math> | ||
| + | #Выбор победителя <math>\mathbf{W_c} \leftarrow ChooseWinner(\mathbf{D_i})</math> | ||
| + | #Вложенный цикл, в котором осуществляется корректировка весов <math>\mathbf{W_i(t+1)}\leftarrow CorrectWeights(\mathbf{W_i(t)})</math> | ||
| − | + | === Схема реализации последовательного алгоритма === | |
| + | Пусть <math>\mathbf{W}</math> - матрица весов, <math>T_{max}</math> - максимальное число "эпох", <math>k</math> - мощность входного множества, <math>N</math> - число нейронов выходного слоя. Тогда схема реализации последовательного алгоритма будет выглядеть следующим образом: | ||
| − | + | <math>\mathbf{W} := InitializeWeights()</math> | |
| − | + | <math>\mathbf{FOR} \ t:=1 \ \mathbf{TO} \ T_{max} \ \mathbf{DO}</math> | |
| + | <math> \quad \mathbf{X} := ChooseRandomVector\left( \{1, \dots, k\} \right)</math> | ||
| + | <math>\mathbf{FOR} \ i:=1 \ \mathbf{TO} \ N \ \mathbf{DO}</math> | ||
| + | <math>\mathbf{D} := CalculateEucledeNorm(\mathbf{X}, \mathbf{W_i})</math> | ||
| + | <math>\mathbf{W_c} := ChooseWinner(\mathbf{D})</math> | ||
| + | <math>\mathbf{FOR} \ i:=1 \ \mathbf{TO} \ N \ \mathbf{DO} \ \mathbf{AND} \ \mathbf{i} \neq \mathbf{c}</math> | ||
| + | <math>\mathbf{W_i(t+1)} := CorrectWeights(\mathbf{W_i(t)}, \mathbf{W_c})</math> | ||
| − | === | + | === Последовательная сложность алгоритма === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Рассмотрим вычислительную сложность описанного алгоритма. Основная часть операций алгоритма приходится на вложенные циклы, где | |
| − | </math> | + | *выполняется вычисление <math>n</math> евклидовых норм, (функция <math>CalculateEucledeNorm</math>), на вычисление каждой из которых требуется по <math>2m-1</math> операций сложения, <math>m</math> операций умножения и один квадратный корень. (<math>m</math> - размерность входных векторов) для вычисления всех норм |
| + | *количество операций на корректировку весов одного нейрона можно оценить как <math>O(m)</math>. | ||
| − | + | Итак, как уже было сказано, общая последовательная сложность алгоритма составляет <math>O(Tmn)</math>, где <math>T</math> - количество эпох обучения (итераций), <math>m</math> - размерность входных векторов (иначе говоря, количество нейронов во входном слое сети Кохонена), <math>n</math> - количество кластеров (иначе говоря, количество нейронов во втором слое сети - слое Кохонена). | |
=== Информационный граф === | === Информационный граф === | ||
| + | Общая схема работы алгоритма выглядит следующим образом: | ||
| + | [[Файл:Graph2.png|thumb|400px|center| Рис. 3. Общая схема работы алгоритма кластеризации]] | ||
| + | Здесь In - входные данные, Init - шаг, на котором происходит инициализация весов, Norm - вычисление расстояний, Win - выбор победителя, Correct - корректировка весов, Out - выходные данные. | ||
| + | |||
| + | Опишем информационный граф алгоритма. | ||
| + | |||
| + | '''Первый этап''' состоит из <math>n</math> параллельных операций вычисления евклидового расстояния до случайно выбранного входного вектора. | ||
| + | |||
| + | На выходе из каждой ветки получаем значение расстояние соответствующего нейрона. | ||
| + | Далее находим минимальное расстояние, тем самым определим нейрона победителя. | ||
| + | |||
| + | [[Файл:Graph3.png|thumb|600px|center| Рис. 4. Первый этап алгоритма]] | ||
| + | |||
| + | |||
| + | '''Второй этап''' состоит их <math>n</math> параллельных операций коррекций весов. | ||
| + | |||
| + | [[Файл:Graph4.png|thumb|600px|center| Рис. 5. Второй этап алгоритма]] | ||
| + | |||
| + | На выходе, собрав из каждой ветки откорректированный вектор весов, получаем обновленную матрицу весов, которая используется на следующей эпохе. | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| + | |||
| + | Для алгоритма кластеризации сетями Кохонена средних имеет место массовый параллелизм: в основе каждого из основных этапов алгоритма (поиска евклидовых расстояний для определения нейрона-победителя и обновления весов) лежат информационно независимые действия. | ||
| + | Учитывая данный факт можно оценить параллельную сложность алгоритма в предположении доступности неограниченного числа необходимых процессоров. | ||
| + | |||
| + | Итоговая сложность параллельного алгоритма будет определяться, исходя из формулы <math>Complexity = T * (PComplexity_{Norm} + PComplexity_{Winner} + PComplexity_{Correct})</math>, где <math>PComplexity_{Norm}</math> - параллельная сложность поиска евклидовых расстояний для определения нейрона-победителя, <math>PComplexity_{Correct}</math> - параллельная сложность обновления весов нейронов, <math>PComplexity_{Winner}</math> - сложность глобального поиска минимального значения расстояния, <math>T</math> - количество эпох (итераций) алгоритма. | ||
| + | |||
| + | Этап Norm заключается в параллельном вычислении евклидовых норм. Сложность этого этапа можно оценить с учетом доступности неограниченного числа процессоров как <math>O(\log m)</math>, где <math>m</math> - длина векторов. | ||
| + | Этап Winner заключается в поиске минимума по подсчитанным расстояниям для определения нейрона-победителя. Параллельная сложность реализации операции нахождения минимума из <math>n</math> элементов определяется как <math>O(\log n)</math>. | ||
| + | Этап Correct состоит из нескольких операций, но асимптотически сложность определяет именно подсчет евклидова расстояния. Аналогично получаем, что сложность данного этапа составляет <math>O(\log m)</math>. | ||
| + | |||
| + | Итоговую параллельную сложность кластеризации сетями Кохонена можно оценить как <math>O(T * \log max(m,n))</math>. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
'''Входные данные:''' множество входных векторов (нейронов первого уровня), множество кластеров (выходов, нейронов второго уровня), максимальное число "эпох" <math>T_{max}</math>, константа <math> \delta </math>, константы <math>A</math> и <math>B</math>, константа <math>c</math> (в случае, если выбрана простая константа). | '''Входные данные:''' множество входных векторов (нейронов первого уровня), множество кластеров (выходов, нейронов второго уровня), максимальное число "эпох" <math>T_{max}</math>, константа <math> \delta </math>, константы <math>A</math> и <math>B</math>, константа <math>c</math> (в случае, если выбрана простая константа). | ||
| − | '''Выходные данные:''' матрица весов | + | '''Объем входные данных:''' так как обучение происходит не на всем входном векторе, а только на количестве векторов равном <math>T</math>, то алгоритм может быть организован так, чтобы принять на выход только <math>T</math> случайных векторов из исходной выборки. И, соответственно, объем входных данных можно считать равным <math>m*T</math>. |
| + | |||
| + | '''Выходные данные:''' матрица весов. | ||
| + | |||
| + | '''Объем выходных данных:''' равен <math>m*k</math> | ||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| + | <p><b>[[глоссарий#Вычислительная мощность|''Вычислительная мощность'']]</b></p> | ||
| + | Вычислительная мощность алгоритма кластеризации сетями Кохонена равна <math>\frac{m*n*T}{m*k+m*n} = \frac{n*T}{k+n}</math>, где, напомним, <math>T</math> - число итераций, <math>n</math> - число нейронов выходного слоя, <math>k</math> - мощность входного множества. | ||
| + | |||
| + | <p><b>[[глоссарий#Детерминированность |''Детерминированность'']] и [[глоссарий#Устойчивость |''Устойчивость'']] </b></p> | ||
| + | Описанный алгоритм кластеризации случайно выбирает элемент входного множества, следовательно, не является детерминированным. Как и все простые сети, построенный алгоритм является устойчивым. | ||
| + | |||
| + | <p><b>''Сильные и слабые стороны алгоритма''</b></p> | ||
| + | |||
| + | Устойчивость к зашумленным данным, быстрое и неуправляемое обучение, возможность упрощения многомерных входных данных с помощью визуализации. | ||
| + | Главное преимущество самоорганизующихся карт Кохонена является их способность "проецирования" многомерных пространств на двумерное. Важной особенностью карт Кохонена является то, что объекты с похожими характеристиками (по всем компонентам) располагаются рядом, образуя кластеры. | ||
| + | |||
| + | Визуализация данных в виде двумерной карты позволяет проводить кластеризацию данных и значительно упрощает корреляционный анализ. | ||
| + | Важным недостатком является то, что окончательный результат работы нейронных сетей зависит от начальных установок сети. С другой стороны, нейронные сети теоретически могут аппроксимировать любую непрерывную функцию, что позволяет исследователю не принимать заранее какие-либо гипотезы относительно модели. | ||
| + | |||
| + | == Программная реализация алгоритма== | ||
| + | ===Особенности реализации последовательного алгоритма=== | ||
| + | === Локальность данных и вычислений === | ||
| + | ==== Локальность реализации алгоритма ==== | ||
| + | ===== Структура обращений в память и качественная оценка локальности ===== | ||
| + | ===== Количественная оценка локальности ===== | ||
| + | |||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| + | === Масштабируемость алгоритма и его реализации === | ||
| + | ==== Масштабируемость алгоритма ==== | ||
| + | |||
| + | Как было описано в [[1.8 | п. 1.8]], для алгоритма кластеризации имеет место массовый параллелизм, поскольку основные этапы алгоритма (поиск евклидовых расстояний для определения нейрона-победителя и обновление весов) информационно независимы, что означает хорошую масштабируемость алгоритма. | ||
| + | |||
| + | ==== Масштабируемость реализации алгоритма ==== | ||
| + | |||
| + | Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Алгоритм был реализован с помощью языка Fortran 90. | ||
| + | |||
| + | Реализация тестировалась со следующими параметрами: | ||
| + | |||
| + | * число процессоров [1 : 128]; | ||
| + | * размер входного слоя сети, а также слоя Кохонена (были установлены равными друг другу) [1000 : 4000]. | ||
| + | |||
| + | |||
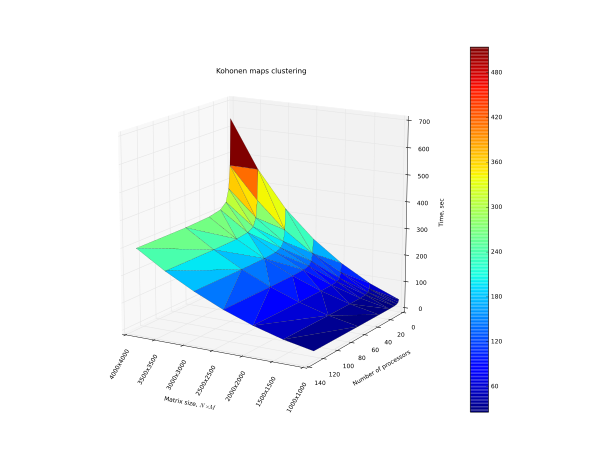
| + | [[Файл:Plot_s2.svg|thumb|600px|center| На рисунке представлен график зависимости времени выполнения от числа процессоров и размерности входных данных]] | ||
| + | |||
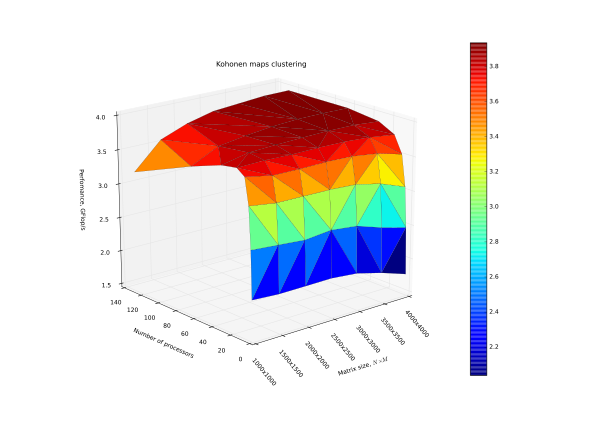
| + | [[Файл:Plot_s3.svg|thumb|600px|center| Производительность в зависимости от числа процессоров и размерности входных данных]] | ||
| + | |||
| + | Можно сделать вывод, что с протестированными параметрами запуска, алгоритм хорошо параллелится только до момента, когда начинают расти накладные расходы, и для максимальных протестированных размеров слоев сети, оптимальным количество процессоров является 32. Из графиков видно, что при увеличении объема задачи эффективность от большего, чем 32, количества процессоров будет расти. | ||
| + | |||
| + | Была использована следующая авторская реализация алгоритма. | ||
| + | |||
| + | program Kohonen | ||
| + | implicit none | ||
| + | include 'mpif.h' | ||
| + | integer rank,ierr,size,sizeBlock | ||
| + | integer n,perProc,i,j,k,jmin,jAbsWin | ||
| + | integer iterNum,IOS | ||
| + | real learning_rate | ||
| + | real dist,prom,minDist | ||
| + | real, allocatable :: W(:,:),sample(:,:),maswin(:,:) | ||
| + | real, allocatable :: buf(:,:),win(:) | ||
| + | double precision start,finish | ||
| + | character str | ||
| + | |||
| + | iterNum = 1000 | ||
| + | n=1000 | ||
| + | |||
| + | learning_rate = 1.0 | ||
| + | |||
| + | allocate(W(n,n)) | ||
| + | allocate(sample(iterNum,n)) | ||
| + | allocate(win(2)) | ||
| + | |||
| + | call randMatr(sample,iterNum,n,.FALSE.) | ||
| + | call randMatr(W,n,n,.True.) | ||
| + | |||
| + | call MPI_INIT(IERR) | ||
| + | call MPI_COMM_SIZE(MPI_COMM_WORLD,SIZE,IERR) | ||
| + | call MPI_COMM_RANK(MPI_COMM_WORLD,RANK,IERR) | ||
| + | |||
| + | perProc = n/size | ||
| + | allocate(buf(n,perProc)) | ||
| + | allocate(maswin(2,size)) | ||
| + | sizeBlock = perProc * n | ||
| + | |||
| + | if (rank .eq. 0) then | ||
| + | start = MPI_WTIME(IERR) | ||
| + | end if | ||
| + | |||
| + | do i=1,IterNum,1 | ||
| + | call obnul(buf,n,perProc) | ||
| + | call MPI_SCATTER(W,sizeBlock,MPI_REAL,buf,sizeBlock,MPI_REAL,0,MPI_COMM_WORLD,IERR) | ||
| + | |||
| + | dist = euclDist(sample(i,1:n),buf(1:n,1),n) | ||
| + | do j=1,perProc,1 | ||
| + | prom = euclDist(sample(i,1:n),buf(1:n,j),n) | ||
| + | if (prom .le. dist) then | ||
| + | dist = prom | ||
| + | jmin = j + rank*perProc | ||
| + | end if | ||
| + | enddo | ||
| + | win(1) = jmin | ||
| + | win(2) = dist | ||
| + | |||
| + | call MPI_BARRIER(MPI_COMM_WORLD,IERR) | ||
| + | |||
| + | call MPI_GATHER(win,2,MPI_REAL,maswin,2,MPI_REAL,0,MPI_COMM_WORLD,IERR) | ||
| + | |||
| + | if (rank .eq. 0) then | ||
| + | minDist = maswin(2,1) | ||
| + | jAbsWin = maswin(1,1) | ||
| + | do j=2,size,1 | ||
| + | if (mindist .ge. maswin(2,j)) then | ||
| + | minDist = maswin(2,j) | ||
| + | jAbsWin = maswin(1,j) | ||
| + | endif | ||
| + | enddo | ||
| + | call modW(W,n,learning_rate,i,jAbsWin) | ||
| + | end if | ||
| + | enddo | ||
| + | |||
| + | if (rank .eq. 0) then | ||
| + | finish = MPI_WTIME(IERR) | ||
| + | open(1,file="Rezult.txt",iostat=IOS) | ||
| + | do while (.NOT. eof(1)) | ||
| + | read(1,*) str | ||
| + | enddo | ||
| + | write (1,*) 'Neurons: ',n,'Processes: ',size,'Time: ',finish-start | ||
| + | close(1) | ||
| + | end if | ||
| + | |||
| + | call MPI_FINALIZE(IERR) | ||
| + | |||
| + | !call printm(W,n,n) | ||
| + | |||
| + | deallocate(W,sample,win,maswin,buf) | ||
| + | |||
| + | |||
| + | contains | ||
| + | |||
| + | subroutine printm(W,a,b) | ||
| + | integer a,b,i,j | ||
| + | real W(n,n) | ||
| + | |||
| + | do j=1,b,1 | ||
| + | write(*,*)(W(i,j), i=1,a) | ||
| + | enddo | ||
| + | end subroutine printm | ||
| + | |||
| + | subroutine obnul(W,a,b) | ||
| + | integer a,b | ||
| + | integer i,j | ||
| + | real W(a,b) | ||
| + | |||
| + | do j=1,b,1 | ||
| + | do i=1,a,1 | ||
| + | W(i,j) = 0.0 | ||
| + | enddo | ||
| + | enddo | ||
| + | end subroutine obnul | ||
| + | |||
| + | real function euclDist(a,b,n) | ||
| + | integer n,i | ||
| + | real a(n),b(n),res | ||
| + | |||
| + | res = 0 | ||
| + | do i = 1,n,1 | ||
| + | res = res + (a(i) - b(i)) * (a(i) - b(i)) | ||
| + | enddo | ||
| + | |||
| + | euclDist = sqrt(res) | ||
| + | end function euclDist | ||
| + | |||
| + | subroutine modW(W,n,learning_rate,iter,jAbsWin) | ||
| + | integer n,iter,JAbsWin | ||
| + | real learning_rate,W(n,n) | ||
| + | integer i,j | ||
| + | |||
| + | do j=1,n,1 | ||
| + | if (j .ne. jAbsWin) then | ||
| + | do i=1,n,1 | ||
| + | W(i,j) = W(i,j) + learning_rate/sqrt(iter+1.0)*(W(i,jAbsWin)-W(i,j)) | ||
| + | enddo | ||
| + | end if | ||
| + | enddo | ||
| + | end subroutine modW | ||
| + | |||
| + | subroutine randMatr(matr,a,b,small) | ||
| + | integer a,b | ||
| + | logical small | ||
| + | integer i,j | ||
| + | real matr(a,b),x | ||
| + | |||
| + | do j=1,b,1 | ||
| + | do i=1,a,1 | ||
| + | call random_seed | ||
| + | call random_number(x) | ||
| + | x = x * 10 - x * 8 | ||
| + | if (small) then | ||
| + | x = x / 40 | ||
| + | end if | ||
| + | matr(i,j) = x | ||
| + | enddo | ||
| + | enddo | ||
| + | end subroutine randMatr | ||
| + | end program Kohonen | ||
| + | |||
| + | === Динамические характеристики и эффективность реализации алгоритма === | ||
| + | === Выводы для классов архитектур === | ||
| + | === Существующие реализации алгоритма === | ||
| + | |||
| + | Последовательные реализации: | ||
| + | |||
| + | * [https://cran.r-project.org/web/packages/kohonen/ kohonen] Бибилиотека для R | ||
| + | * [https://pypi.python.org/pypi/kohonen kohonen] Бибилиотека для Python | ||
| + | * [http://knnl.sourceforge.net/ KNNL]: C++ бибилиотека. | ||
| + | * [https://www.mathworks.com/help/nnet/ug/cluster-with-self-organizing-map-neural-network.html?requestedDomain=www.mathworks.com Matlab realization]: Реализация в Matlab. | ||
| + | * [http://jknnl.sourceforge.net/ JKNNL]: Библиотека для Java. | ||
| + | * [https://support.sas.com/documentation/onlinedoc/miner/casestudy_59123.pdf SAS EM]: Реализация в SAS Enterprise Miner | ||
| + | |||
| + | |||
| + | |||
| + | Параллельные реализации: | ||
| + | |||
| + | * [https://github.com/peterwittek/somoclu Somoclu]: Библиотека для Python, R, Julia, и Matlab с поддержкой OpenMP, MPI и CUDA. | ||
| + | |||
| + | = Литература = | ||
| + | |||
| + | # Teuvo Kohonen, Self-Organizing Maps/Helsinki University of Technology,1997/Second Edition. | ||
| + | # Нейский И.М. Классификация и сравнение методов кластеризации http://it-claim.ru/Persons/Neyskiy/Article2_Neiskiy.pdf | ||
Текущая версия на 15:33, 7 декабря 2016
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 07.12.2016 Данная работа соответствует формальным критериям. Проверено Teplov. |
| Кластеризация сетями Кохонена | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(mnT)[/math] |
| Объём входных данных | [math]mk[/math] |
| Объём выходных данных | [math]mn[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(T*log(max(m,n)))[/math] |
| Ширина ярусно-параллельной формы | [math]O(mn)[/math] |
Авторы страницы Егор Максимов (1.1, 1.2, 1.4, 1.5, 1.6, 1.7, 1.9, 2.4, 1.10) и Кирилл Кравцов (1.2, 1.3, 1.6, 1.7, 1.8, 1.9, 1.10, 2.4, 2.7)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Искусственная нейронная сеть Кохонена или самоорганизующаяся карта признаков (SOM) была предложена финским исследователем Тойво Кохоненом в начале 1980-х годов.
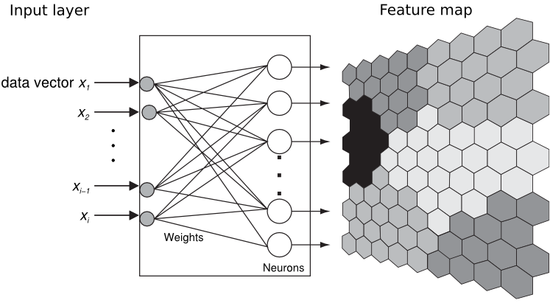
Она представляет собой двухслойную сеть. Каждый нейрон первого (распределительного) слоя соединен со всеми нейронами второго (выходного) слоя, которые расположены в виде двумерной решетки. Для визуализации топологии слоя Кохонена используют либо шестиугольные, либо прямоугольные ячейки, в которых распологаются нейроны. Шестиугольные ячейки часто являются более предпочтительными, так как расстояние от центра выбранной ячейки до ее соседей одинаково.Нейроны выходного слоя называются кластерными элементами, их количество определят максимальное количество групп, на которые система может разделить входные данные. Увеличивая количество нейронов второго слоя можно увеличивать детализацию результатов процесса кластеризации.
Система работает по принципу соревнования – нейроны второго слоя соревнуются друг с другом за право наилучшим образом сочетаться с входным вектором сигналов, побеждает тот элемент-нейрон, чей вектор весов ближе всего к входному вектору сигналов. За меру близости двух векторов можно взять квадрат евклидова расстояния. Таким образом, каждый входной вектор относится к некоторому кластерному элементу.
Для обучения сети Кохонена используется соревновательный метод. На каждом шаге обучения из исходного набора данных случайно выбирается один вектор. Затем производится поиск нейрона выходного слоя, для которого расстояние между его вектором весов и входным вектором - минимально. По определённому правилу производится корректировка весов для нейрона-победителя и нейронов из его окрестности, которая задаётся соответствующей функцией окрестности.
1.2 Математическое описание алгоритма
Пусть имеется некоторое множество векторов [math] x^{(i)}=(x_1^{(i)},x_2^{(i)},...,x_m^{(i)}) \in \mathbb{R}^m, i=1, \dots, k[/math]. Заранее зададим количество кластеров равным [math]n[/math]. Соответственно, Карта Кохонена представляет собой двухслойную fully-connected нейронную сеть, где первый слой состоит из [math]m[/math] нейронов, а второй - из [math]n[/math]. Каждый j-ый нейрон описывается вектором весов [math] w_j=(w_{1j},w_{2j},...,w_{mj}), j=1, \dots, n[/math].
1.2.1 Алгоритм обучения сети без учителя
Обучение состоит из последовательности коррекций векторов, представляющих собой нейроны. Сначала следует инициализировать векторы весов. Далее определенное количество раз (эпох) производятся следующие действия:
- Случайным образов выбирается вектор [math]x(t)[/math] из входных данных.
- Выбирается нейрон-победитель [math]w_c[/math] "наиболее похожий" (по евклидову расстоянию) на вектор [math]x(t)[/math]:
[math] ||x(t)-w_c||=\min\limits_{i}(||x(t)-w_i(t)||)[/math]. - Веса всех нейронов обновляются по формуле:
где [math]t[/math] - номер эпохи, [math] h_{ic}(t)[/math]- функция соседства нейронов, [math]\alpha (t)[/math] - функция скорости обучения сети.
1.2.2 Инициализация начальных весов
Инициализация случайными значениями, когда всем весам даются малые случайные величины. Инициализация примерами, когда в качестве начальных значений задаются значения случайно выбранных примеров из обучающей выборки Линейная инициализация. В этом случае веса инициируются значениями векторов, линейно упорядоченных вдоль линейного подпространства, проходящего между двумя главных собственными векторами исходного набора данных. Собственные вектора могут быть найдены например при помощи процедуры Грама-Шмидта.
1.2.3 Функция соседства нейронов
Функции от расстояния применяются двух видов:
Константа:
[math]
h(d,t) = \begin{cases}
c, & \mbox{if } n \ d\lt =\delta \\
0, & \mbox{if } n \ d\gt \delta
\end{cases}[/math]
Функция Гаусса:
[math]h_{ic}(t)=\exp(-\frac{\|r_c-r_i\|^2}{2\sigma^2(t)})[/math],
где [math]r_i[/math] определяет положение [math]i[/math]-го нейрона в сетке
1.2.4 Функция скорости обучения сети
Главное требование к ней - монотонное убывание при возрастании [math]t[/math] для замедления темпов вариации весов нейронов слоя Кохонена. Функция может быть задана, например, как [math]\alpha(t)=\frac{A}{B+t}[/math], где [math]A[/math] и [math]B[/math] - некоторые константы.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит из двух шагов, повторяющихся каждую итерацию (эпоху):
- Вычисление расстояния от случайно выбранного вектора [math]x(t)[/math] до каждого нейрона и выбор нейрона с наименьшим расстоянием. Т.е. вычисление [math]n[/math] евклидовых расстояний и сортировка полученного массива расстояний. Сложность евклидового расстояния растет линейно с увеличением длины вектора. Следовательно получаем сложность данного шага [math]O(mn)[/math].
- Обновление весов всех нейронов. Пусть используется гауссовская функция для вычисления расстояний между нейронами. Сложность обновления веса одного нейрона линейно зависит от [math]m[/math]. Т.е. сложность данного шага также [math]O(mn)[/math].
В итоге получаем, что для всего алгоритма с количеством эпох равным [math]T[/math] сложность составляет [math]O(Tmn)[/math].
1.4 Макроструктура алгоритма
Алгоритм кластеризации можно разбить на следующие этапы:
- Инициализация [math]\mathbf{W} \leftarrow ComputeInitialWeights(\mathbf{W})[/math]
- Цикл, повторяющийся [math]T_{max}[/math] (максимальное число "эпох") раз:
- [math]\mathbf{X} \leftarrow ChooseRandomVector(\mathbf{V})[/math]
- Вложенный цикл, в котором осуществляется вычисление расстояний [math]\mathbf{D_i} \leftarrow CalculateEucledeNorm(X, \mathbf{W_i})[/math]
- Выбор победителя [math]\mathbf{W_c} \leftarrow ChooseWinner(\mathbf{D_i})[/math]
- Вложенный цикл, в котором осуществляется корректировка весов [math]\mathbf{W_i(t+1)}\leftarrow CorrectWeights(\mathbf{W_i(t)})[/math]
1.5 Схема реализации последовательного алгоритма
Пусть [math]\mathbf{W}[/math] - матрица весов, [math]T_{max}[/math] - максимальное число "эпох", [math]k[/math] - мощность входного множества, [math]N[/math] - число нейронов выходного слоя. Тогда схема реализации последовательного алгоритма будет выглядеть следующим образом:
[math]\mathbf{W} := InitializeWeights()[/math] [math]\mathbf{FOR} \ t:=1 \ \mathbf{TO} \ T_{max} \ \mathbf{DO}[/math] [math] \quad \mathbf{X} := ChooseRandomVector\left( \{1, \dots, k\} \right)[/math] [math]\mathbf{FOR} \ i:=1 \ \mathbf{TO} \ N \ \mathbf{DO}[/math] [math]\mathbf{D} := CalculateEucledeNorm(\mathbf{X}, \mathbf{W_i})[/math] [math]\mathbf{W_c} := ChooseWinner(\mathbf{D})[/math] [math]\mathbf{FOR} \ i:=1 \ \mathbf{TO} \ N \ \mathbf{DO} \ \mathbf{AND} \ \mathbf{i} \neq \mathbf{c}[/math] [math]\mathbf{W_i(t+1)} := CorrectWeights(\mathbf{W_i(t)}, \mathbf{W_c})[/math]
1.6 Последовательная сложность алгоритма
Рассмотрим вычислительную сложность описанного алгоритма. Основная часть операций алгоритма приходится на вложенные циклы, где
- выполняется вычисление [math]n[/math] евклидовых норм, (функция [math]CalculateEucledeNorm[/math]), на вычисление каждой из которых требуется по [math]2m-1[/math] операций сложения, [math]m[/math] операций умножения и один квадратный корень. ([math]m[/math] - размерность входных векторов) для вычисления всех норм
- количество операций на корректировку весов одного нейрона можно оценить как [math]O(m)[/math].
Итак, как уже было сказано, общая последовательная сложность алгоритма составляет [math]O(Tmn)[/math], где [math]T[/math] - количество эпох обучения (итераций), [math]m[/math] - размерность входных векторов (иначе говоря, количество нейронов во входном слое сети Кохонена), [math]n[/math] - количество кластеров (иначе говоря, количество нейронов во втором слое сети - слое Кохонена).
1.7 Информационный граф
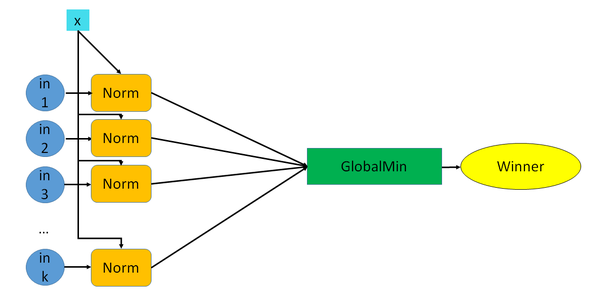
Общая схема работы алгоритма выглядит следующим образом:
Здесь In - входные данные, Init - шаг, на котором происходит инициализация весов, Norm - вычисление расстояний, Win - выбор победителя, Correct - корректировка весов, Out - выходные данные.
Опишем информационный граф алгоритма.
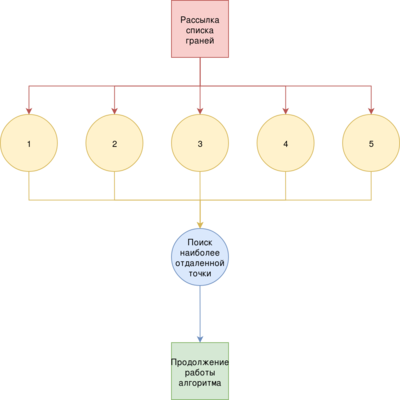
Первый этап состоит из [math]n[/math] параллельных операций вычисления евклидового расстояния до случайно выбранного входного вектора.
На выходе из каждой ветки получаем значение расстояние соответствующего нейрона. Далее находим минимальное расстояние, тем самым определим нейрона победителя.
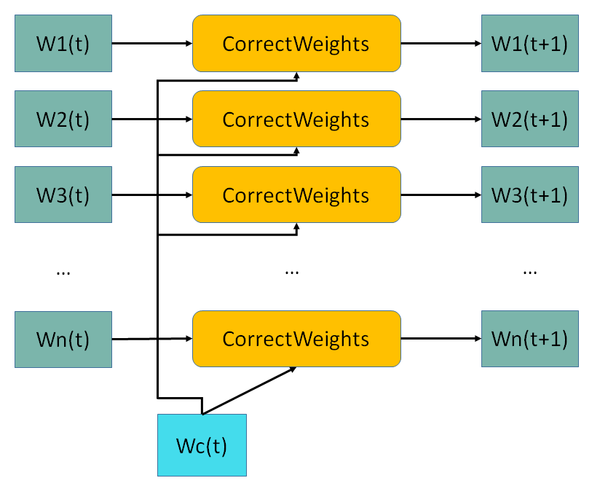
Второй этап состоит их [math]n[/math] параллельных операций коррекций весов.
На выходе, собрав из каждой ветки откорректированный вектор весов, получаем обновленную матрицу весов, которая используется на следующей эпохе.
1.8 Ресурс параллелизма алгоритма
Для алгоритма кластеризации сетями Кохонена средних имеет место массовый параллелизм: в основе каждого из основных этапов алгоритма (поиска евклидовых расстояний для определения нейрона-победителя и обновления весов) лежат информационно независимые действия. Учитывая данный факт можно оценить параллельную сложность алгоритма в предположении доступности неограниченного числа необходимых процессоров.
Итоговая сложность параллельного алгоритма будет определяться, исходя из формулы [math]Complexity = T * (PComplexity_{Norm} + PComplexity_{Winner} + PComplexity_{Correct})[/math], где [math]PComplexity_{Norm}[/math] - параллельная сложность поиска евклидовых расстояний для определения нейрона-победителя, [math]PComplexity_{Correct}[/math] - параллельная сложность обновления весов нейронов, [math]PComplexity_{Winner}[/math] - сложность глобального поиска минимального значения расстояния, [math]T[/math] - количество эпох (итераций) алгоритма.
Этап Norm заключается в параллельном вычислении евклидовых норм. Сложность этого этапа можно оценить с учетом доступности неограниченного числа процессоров как [math]O(\log m)[/math], где [math]m[/math] - длина векторов. Этап Winner заключается в поиске минимума по подсчитанным расстояниям для определения нейрона-победителя. Параллельная сложность реализации операции нахождения минимума из [math]n[/math] элементов определяется как [math]O(\log n)[/math]. Этап Correct состоит из нескольких операций, но асимптотически сложность определяет именно подсчет евклидова расстояния. Аналогично получаем, что сложность данного этапа составляет [math]O(\log m)[/math].
Итоговую параллельную сложность кластеризации сетями Кохонена можно оценить как [math]O(T * \log max(m,n))[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: множество входных векторов (нейронов первого уровня), множество кластеров (выходов, нейронов второго уровня), максимальное число "эпох" [math]T_{max}[/math], константа [math] \delta [/math], константы [math]A[/math] и [math]B[/math], константа [math]c[/math] (в случае, если выбрана простая константа).
Объем входные данных: так как обучение происходит не на всем входном векторе, а только на количестве векторов равном [math]T[/math], то алгоритм может быть организован так, чтобы принять на выход только [math]T[/math] случайных векторов из исходной выборки. И, соответственно, объем входных данных можно считать равным [math]m*T[/math].
Выходные данные: матрица весов.
Объем выходных данных: равен [math]m*k[/math]
1.10 Свойства алгоритма
Вычислительная мощность алгоритма кластеризации сетями Кохонена равна [math]\frac{m*n*T}{m*k+m*n} = \frac{n*T}{k+n}[/math], где, напомним, [math]T[/math] - число итераций, [math]n[/math] - число нейронов выходного слоя, [math]k[/math] - мощность входного множества.
Детерминированность и Устойчивость
Описанный алгоритм кластеризации случайно выбирает элемент входного множества, следовательно, не является детерминированным. Как и все простые сети, построенный алгоритм является устойчивым.
Сильные и слабые стороны алгоритма
Устойчивость к зашумленным данным, быстрое и неуправляемое обучение, возможность упрощения многомерных входных данных с помощью визуализации. Главное преимущество самоорганизующихся карт Кохонена является их способность "проецирования" многомерных пространств на двумерное. Важной особенностью карт Кохонена является то, что объекты с похожими характеристиками (по всем компонентам) располагаются рядом, образуя кластеры.
Визуализация данных в виде двумерной карты позволяет проводить кластеризацию данных и значительно упрощает корреляционный анализ. Важным недостатком является то, что окончательный результат работы нейронных сетей зависит от начальных установок сети. С другой стороны, нейронные сети теоретически могут аппроксимировать любую непрерывную функцию, что позволяет исследователю не принимать заранее какие-либо гипотезы относительно модели.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
Как было описано в п. 1.8, для алгоритма кластеризации имеет место массовый параллелизм, поскольку основные этапы алгоритма (поиск евклидовых расстояний для определения нейрона-победителя и обновление весов) информационно независимы, что означает хорошую масштабируемость алгоритма.
2.4.2 Масштабируемость реализации алгоритма
Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Алгоритм был реализован с помощью языка Fortran 90.
Реализация тестировалась со следующими параметрами:
- число процессоров [1 : 128];
- размер входного слоя сети, а также слоя Кохонена (были установлены равными друг другу) [1000 : 4000].
Можно сделать вывод, что с протестированными параметрами запуска, алгоритм хорошо параллелится только до момента, когда начинают расти накладные расходы, и для максимальных протестированных размеров слоев сети, оптимальным количество процессоров является 32. Из графиков видно, что при увеличении объема задачи эффективность от большего, чем 32, количества процессоров будет расти.
Была использована следующая авторская реализация алгоритма.
program Kohonen
implicit none
include 'mpif.h'
integer rank,ierr,size,sizeBlock
integer n,perProc,i,j,k,jmin,jAbsWin
integer iterNum,IOS
real learning_rate
real dist,prom,minDist
real, allocatable :: W(:,:),sample(:,:),maswin(:,:)
real, allocatable :: buf(:,:),win(:)
double precision start,finish
character str
iterNum = 1000
n=1000
learning_rate = 1.0
allocate(W(n,n))
allocate(sample(iterNum,n))
allocate(win(2))
call randMatr(sample,iterNum,n,.FALSE.)
call randMatr(W,n,n,.True.)
call MPI_INIT(IERR)
call MPI_COMM_SIZE(MPI_COMM_WORLD,SIZE,IERR)
call MPI_COMM_RANK(MPI_COMM_WORLD,RANK,IERR)
perProc = n/size
allocate(buf(n,perProc))
allocate(maswin(2,size))
sizeBlock = perProc * n
if (rank .eq. 0) then
start = MPI_WTIME(IERR)
end if
do i=1,IterNum,1
call obnul(buf,n,perProc)
call MPI_SCATTER(W,sizeBlock,MPI_REAL,buf,sizeBlock,MPI_REAL,0,MPI_COMM_WORLD,IERR)
dist = euclDist(sample(i,1:n),buf(1:n,1),n)
do j=1,perProc,1
prom = euclDist(sample(i,1:n),buf(1:n,j),n)
if (prom .le. dist) then
dist = prom
jmin = j + rank*perProc
end if
enddo
win(1) = jmin
win(2) = dist
call MPI_BARRIER(MPI_COMM_WORLD,IERR)
call MPI_GATHER(win,2,MPI_REAL,maswin,2,MPI_REAL,0,MPI_COMM_WORLD,IERR)
if (rank .eq. 0) then
minDist = maswin(2,1)
jAbsWin = maswin(1,1)
do j=2,size,1
if (mindist .ge. maswin(2,j)) then
minDist = maswin(2,j)
jAbsWin = maswin(1,j)
endif
enddo
call modW(W,n,learning_rate,i,jAbsWin)
end if
enddo
if (rank .eq. 0) then
finish = MPI_WTIME(IERR)
open(1,file="Rezult.txt",iostat=IOS)
do while (.NOT. eof(1))
read(1,*) str
enddo
write (1,*) 'Neurons: ',n,'Processes: ',size,'Time: ',finish-start
close(1)
end if
call MPI_FINALIZE(IERR)
!call printm(W,n,n)
deallocate(W,sample,win,maswin,buf)
contains
subroutine printm(W,a,b)
integer a,b,i,j
real W(n,n)
do j=1,b,1
write(*,*)(W(i,j), i=1,a)
enddo
end subroutine printm
subroutine obnul(W,a,b)
integer a,b
integer i,j
real W(a,b)
do j=1,b,1
do i=1,a,1
W(i,j) = 0.0
enddo
enddo
end subroutine obnul
real function euclDist(a,b,n)
integer n,i
real a(n),b(n),res
res = 0
do i = 1,n,1
res = res + (a(i) - b(i)) * (a(i) - b(i))
enddo
euclDist = sqrt(res)
end function euclDist
subroutine modW(W,n,learning_rate,iter,jAbsWin)
integer n,iter,JAbsWin
real learning_rate,W(n,n)
integer i,j
do j=1,n,1
if (j .ne. jAbsWin) then
do i=1,n,1
W(i,j) = W(i,j) + learning_rate/sqrt(iter+1.0)*(W(i,jAbsWin)-W(i,j))
enddo
end if
enddo
end subroutine modW
subroutine randMatr(matr,a,b,small)
integer a,b
logical small
integer i,j
real matr(a,b),x
do j=1,b,1
do i=1,a,1
call random_seed
call random_number(x)
x = x * 10 - x * 8
if (small) then
x = x / 40
end if
matr(i,j) = x
enddo
enddo
end subroutine randMatr
end program Kohonen
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Последовательные реализации:
- kohonen Бибилиотека для R
- kohonen Бибилиотека для Python
- KNNL: C++ бибилиотека.
- Matlab realization: Реализация в Matlab.
- JKNNL: Библиотека для Java.
- SAS EM: Реализация в SAS Enterprise Miner
Параллельные реализации:
- Somoclu: Библиотека для Python, R, Julia, и Matlab с поддержкой OpenMP, MPI и CUDA.
3 Литература
- Teuvo Kohonen, Self-Organizing Maps/Helsinki University of Technology,1997/Second Edition.
- Нейский И.М. Классификация и сравнение методов кластеризации http://it-claim.ru/Persons/Neyskiy/Article2_Neiskiy.pdf