Участник:Obirvalger/Метод рекурсивной координатной бисекции: различия между версиями
Dan (обсуждение | вклад) |
|||
| (не показано 47 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Авторы: [[Участник:Obirvalger|Гордеев Михаил]], [[Участник:KolmakovEA|Колмаков Евгений]]. | + | {{Assignment|Dan}} |
| + | {{algorithm | ||
| + | | name = Рекурсивная координатная бисекция | ||
| + | | serial_complexity = <math>O(n \log_2{n} \log_2{k})</math> | ||
| + | | pf_height = <math>\log_2{k}</math> | ||
| + | | pf_width = <math>k</math> | ||
| + | | input_data = <math>N|V| + |G|</math> | ||
| + | | output_data = <math>|V|</math> | ||
| + | }} | ||
| + | |||
| + | Авторы: [[Участник:Obirvalger|Гордеев Михаил]] (разделы 1.4, 1.6, 1.8, 1.10, 2.1, 2.4), [[Участник:KolmakovEA|Колмаков Евгений]] (разделы 1.1, 1.2, 1.3, 1.5, 1.7, 1.9, 2.1, 2.4, 2.7). | ||
= Свойства и структура алгоритмов = | = Свойства и структура алгоритмов = | ||
| Строка 7: | Строка 17: | ||
=== Задача декомпозиции графа === | === Задача декомпозиции графа === | ||
| − | '''Метод рекурсивной координатной бисекции''' является одним из методов, применяемых для декомпозиции графов. В прикладных задачах, как правило, граф | + | '''Метод рекурсивной координатной бисекции''' является одним из методов, применяемых для декомпозиции графов <ref>Якобовский М.В. Введение в параллельные методы решения задач: Учебное пособие / Предисл.: В. А. Садовничий. – М.: Издательство Московского университета, 2012. – 328 с., илл. – (Серия «Суперкомпьютерное образование»), ISBN 978-5-211-06382-2 URL: http://lira.imamod.ru/ITTPMOPS/</ref>. В прикладных задачах, как правило, граф |
представляет собой сетку в пространстве некоторой размерности. При численном решении задач механики сплошной среды с помощью методов конечных разностей или конечных элементов широко используется геометрический параллелизм, при котором сетка, покрывающая расчётную область, разбивается на множество доменов, каждый из которых обрабатывается отдельным процессором. Основная проблема связана с необходимостью решения задачи статистической балансировки загрузки, то есть равномерного распределения вычислительной нагрузки между процессорами за счёт выбора оптимальной декомпозиции сетки. | представляет собой сетку в пространстве некоторой размерности. При численном решении задач механики сплошной среды с помощью методов конечных разностей или конечных элементов широко используется геометрический параллелизм, при котором сетка, покрывающая расчётную область, разбивается на множество доменов, каждый из которых обрабатывается отдельным процессором. Основная проблема связана с необходимостью решения задачи статистической балансировки загрузки, то есть равномерного распределения вычислительной нагрузки между процессорами за счёт выбора оптимальной декомпозиции сетки. | ||
| Строка 66: | Строка 76: | ||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| − | Как записано в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть метода составляют множественные (всего <math>k-1</math>) сортировки (функция | + | Как записано в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть метода составляют множественные (всего <math>k-1</math>) сортировки (функция argsort в коде в [[#Схема реализации последовательного алгоритма |следующем разделе]]). |
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| + | |||
| + | Опишем последовательную реализацию метода рекурсивной координатной бисекции, где выбор оси производится исходя из условия максимизации протяженности вдоль этой оси. Ниже представлен код данного алгоритма на языке Python 3. | ||
| + | |||
| + | <source lang="python"> | ||
| + | # Переменная для хранения результата работы алгоритма | ||
| + | partition = [] | ||
| + | |||
| + | # V - numpy.ndarray размера |V| x N, k - число доменов | ||
| + | def recursive_bisection(V, k): | ||
| + | |||
| + | global partition | ||
| + | |||
| + | # Если текущая часть графа есть домен, добавляем ее к результату разбиения | ||
| + | if (k <= 1): | ||
| + | partition.append(V) | ||
| + | return | ||
| + | |||
| + | # Вычисляем количество доменов в каждой из частей | ||
| + | k1 = (k + 1) / 2 | ||
| + | k2 = k - k1 | ||
| + | |||
| + | # Производим разбиение | ||
| + | V1, V2 = bisect(V, k) | ||
| + | |||
| + | # Рекурсивно разбиваем каждую из частей | ||
| + | recursive_bisect(V1, k1) | ||
| + | recursive_bisect(V2, k2) | ||
| + | |||
| + | def bisect(V, k): | ||
| + | # Вычисляем координату с наибольшей протяженностью | ||
| + | t = V.max(axis=0) - V.min(axis=0) | ||
| + | m = t.argmax() | ||
| + | |||
| + | # Сортируем вершины по координате с номером m | ||
| + | V_sorted = V[V[:, m].argsort()] | ||
| + | |||
| + | # Вычисляем индекс для разбиения в соответствии с числом доменов | ||
| + | ind = (k + 1) * V.shape[0] // (2 * k) | ||
| + | |||
| + | return V_sorted[:ind, :], V_sorted[ind:, :] | ||
| + | </source> | ||
| + | |||
| + | Приведённый код предназначен для более подробного описания основных шагов в алгоритме, представляет собой лишь схему и не является максимально эффективным. Это сделано для того, чтобы код был более наглядным. В более эффективной реализации, например, вместо создания массивов в процедуре bisect можно везде оперировать только индексами. | ||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| Строка 84: | Строка 137: | ||
</center> | </center> | ||
| − | Пусть <math>S(n) = O(n\log_2{n})</math> (например, для сортировки слиянием), тогда по теореме о | + | Пусть <math>S(n) = O(n\log_2{n})</math> (например, для сортировки слиянием), тогда по теореме о рекуррентных соотношениях <ref>https://ru.wikipedia.org/wiki/Основная_теорема_о_рекуррентных_соотношениях</ref> для произвольного положительного <math>\varepsilon</math> имеет место оценка <math>D(n) \lesssim n^{1+\varepsilon}</math>. |
| − | Величину <math>D_k(n)</math> можно явно посчитать по формуле <math>\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}2^i S(\frac{n}{2^i})</math>. Если использовать сортировку со сложностью <math>S(n) = O(n\ | + | Величину <math>D_k(n)</math> можно явно посчитать по формуле <math>\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}2^i S(\frac{n}{2^i})</math>. Если использовать сортировку со сложностью <math>S(n) = O(n\log_2{n})</math>, то |
<center> | <center> | ||
| − | <math>D_k(n) = </math> <math>O(\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}2^i \frac{n}{2^i} \log_2{\frac{n}{2^i}}) = </math> <math>O(n\log_2(\prod\limits_{i=0}^{\lceil\log_2{k}\rceil}\frac{n}{2^i})) = </math> <math>O(n\log_2{\frac{n^{\log_2{k}}}{2^\frac{\log_2{k}(\log_2{k}+1))}{2}}}) =</math> <math> O(n(\log_2{n}\log_2{k} - \frac{\log^2_2{k}}{2})) = </math> <math>O(n\ | + | <math>D_k(n) = </math> <math>O(\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}2^i \frac{n}{2^i} \log_2{\frac{n}{2^i}}) = </math> <math>O(n\log_2(\prod\limits_{i=0}^{\lceil\log_2{k}\rceil}\frac{n}{2^i})) = </math> <math>O(n\log_2{\frac{n^{\log_2{k}}}{2^\frac{\log_2{k}(\log_2{k}+1))}{2}}}) =</math> <math> O(n(\log_2{n}\log_2{k} - \frac{\log^2_2{k}}{2})) = </math> <math>O(n\log_2{n}\log_2{k})</math>. |
</center> | </center> | ||
== Информационный граф == | == Информационный граф == | ||
| + | |||
| + | Под операцией в данном пункте будем понимать макрооперацию сортировки. Передача данных происходит после разбиения множества вершин на две части. | ||
| + | Таким образом, информационный граф представляет из себя бинарное дерево с <math>k</math> листьями. На рисунке ниже приведена часть информационного графа для <math>k = 16</math>. Зависимость от числа вершин <math>n</math> учитывается в самих узлах дерева. | ||
| + | |||
| + | <center> | ||
| + | [[Файл:Tree_sort.svg|thumb|center|800px|Рисунок 1. Граф алгоритма.]] | ||
| + | </center> | ||
| + | |||
| + | Высота ярусно-параллельной формы - <math>\log_2{k}</math>. | ||
| + | |||
| + | Ширина ярусно-параллельной формы - <math>k</math>. | ||
| + | |||
| + | Если рассматривать более мелкие операции, используемые в процессе сортировки, то глобально информационный граф будет выглядеть также, однако каждый | ||
| + | узел будет заменён на информационный граф используемого алгоритма сортировки (или <math>N</math> таких графов, если используется критерий минимизации числа разрезов). | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| Строка 97: | Строка 164: | ||
Для декомпозиции графа с <math>n</math> вершинами на <math>k</math> доменов методом рекурсивной координатной бисекции в параллельном варианте требуется последовательно выполнить <math>\lceil\log_2{k}\rceil</math> ярусов. На <math>i</math>-ом ярусе будет выполнятся <math>2^i</math> операций сортировки. | Для декомпозиции графа с <math>n</math> вершинами на <math>k</math> доменов методом рекурсивной координатной бисекции в параллельном варианте требуется последовательно выполнить <math>\lceil\log_2{k}\rceil</math> ярусов. На <math>i</math>-ом ярусе будет выполнятся <math>2^i</math> операций сортировки. | ||
Рассмотрим два случая распараллеливания нашего алгоритма: | Рассмотрим два случая распараллеливания нашего алгоритма: | ||
| − | * Параллельное выполнение операций на каждом ярусе с использованием последовательного алгоритма сортировки со сложностью <math>O(n\ | + | * Параллельное выполнение операций на каждом ярусе с использованием последовательного алгоритма сортировки со сложностью <math>O(n\log_2{n})</math>. |
# На первом шаге один процессор производит сортировку всех вершин, разделяет граф на два подграфа и передает однин из подрафов новому процессору. | # На первом шаге один процессор производит сортировку всех вершин, разделяет граф на два подграфа и передает однин из подрафов новому процессору. | ||
# На <math>i</math>-ом шаге каждый из уже получивший свой граф процессор производит сортировку всех вершин, разделяет граф на два подграфа и передает однин из подрафов новому процессору. | # На <math>i</math>-ом шаге каждый из уже получивший свой граф процессор производит сортировку всех вершин, разделяет граф на два подграфа и передает однин из подрафов новому процессору. | ||
| Строка 103: | Строка 170: | ||
Тогда сложность нашего алгоритма равна: | Тогда сложность нашего алгоритма равна: | ||
<center> | <center> | ||
| − | <math>D_k(n) = O(\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}\frac{n}{2^i} \log_2{\frac{n}{2^i}}) = </math> <math>n\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}(\frac{\log_2{n}}{2^i} - \frac{i}{2^i}) = </math> <math>O(n\log_2{n}) - O(n) = O(n\ | + | <math>D_k(n) = O(\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}\frac{n}{2^i} \log_2{\frac{n}{2^i}}) = </math> <math>n\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}(\frac{\log_2{n}}{2^i} - \frac{i}{2^i}) = </math> <math>O(n\log_2{n}) - O(n) = O(n\log_2{n})</math>. |
</center> | </center> | ||
| Строка 111: | Строка 178: | ||
<center> | <center> | ||
| − | <math>D_k(n) = \sum\limits_{i=0}^{\lceil\log_2{k}\rceil}\log^ | + | <math>D_k(n) = \sum\limits_{i=0}^{\lceil\log_2{k}\rceil}\log^2_2\frac{n}{2^i} = O(\log^2_2{n}\log_2{k}) = O(\log^3_2{n})</math>. |
| + | </center> | ||
| + | Известно <ref>https://en.wikipedia.org/wiki/Sorting_algorithm</ref>, что оптимальная параллельная сортировка имеет сложность <math>O(\log_2{n})</math>. В этом случае | ||
| + | <center> | ||
| + | <math>D_k(n) = \sum\limits_{i=0}^{\lceil\log_2{k}\rceil}\log_2\frac{n}{2^i} = O(\log_2{n}\log_2{k})</math>. | ||
</center> | </center> | ||
| − | |||
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
| Строка 126: | Строка 196: | ||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| − | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов | + | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является ''линейным'' (отношение <math>O(n\log{n})</math> к <math>O(\log{n}))</math>. |
| + | |||
| + | Алгоритм детерминирован в случае использования устойчивой сортировки вершин. Также алгоритм устойчив, так как используются операции, не приводящие к ошибкам округления - это операции сравнения для вещественных чисел и операции с целыми числами. | ||
| + | Наибольшее число операций составляют операции сравнения. | ||
| + | |||
| + | Так как количество вершин на разных процессорах примерно одинаковое алгоритм является сбалансированным по числу операций на каждом процессоре. | ||
| − | Алгоритм | + | Алгоритм достаточно прост и легко модифицируется в зависимости от критерия декомпозиции. |
= Программная реализация алгоритма = | = Программная реализация алгоритма = | ||
== Особенности реализации последовательного алгоритма == | == Особенности реализации последовательного алгоритма == | ||
| + | |||
| + | Ниже приведен пример реализации последовательного алгоритма на языке C++. Следует отметить, что исходный массив вершин не изменяется, вся работа осуществляется с индексами. | ||
| + | <source lang = "c++"> | ||
| + | #include <algorithm> | ||
| + | #include <iostream> | ||
| + | #include <vector> | ||
| + | |||
| + | using namespace std; | ||
| + | |||
| + | #define N 5 | ||
| + | #define M 5 | ||
| + | #define STEP 0.01 | ||
| + | |||
| + | #define N_DIMS 2 | ||
| + | #define N_DOMAINS 6 | ||
| + | |||
| + | vector<vector<double> > points_matrix(N_DIMS, vector<double>(N * M)); | ||
| + | vector<vector<int> > graph_partition; | ||
| + | |||
| + | double span(vector<double> x, vector<int> idx) | ||
| + | { | ||
| + | double max_value = x[idx[0]]; | ||
| + | double min_value = x[idx[0]]; | ||
| + | |||
| + | for (size_t i = 1; i < idx.size(); i++) { | ||
| + | max_value = (x[idx[i]] > max_value) ? x[idx[i]] : max_value; | ||
| + | min_value = (x[idx[i]] < min_value) ? x[idx[i]] : min_value; | ||
| + | } | ||
| + | |||
| + | return max_value; | ||
| + | } | ||
| + | |||
| + | vector<int> bisect(vector<int> idx) | ||
| + | { | ||
| + | double max_span = 0; | ||
| + | double max_ind = 0; | ||
| + | |||
| + | // finding coordinate with maximal span | ||
| + | for (size_t i = 0; i < points_matrix.size(); i++) { | ||
| + | double cur_span = span(points_matrix[i], idx); | ||
| + | if (cur_span > max_span) { | ||
| + | max_span = cur_span; | ||
| + | max_ind = i; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | // sorting vertices along this coordinate | ||
| + | sort(idx.begin(), idx.end(), [&](const int& a, const int& b) { | ||
| + | return points_matrix[max_ind][a] < points_matrix[max_ind][b]; | ||
| + | }); | ||
| + | |||
| + | return idx; | ||
| + | } | ||
| + | |||
| + | void recursive_bisection(vector<int> idx, int k) | ||
| + | { | ||
| + | // adding current domain to partition | ||
| + | if (k < 2) { | ||
| + | graph_partition.push_back(idx); | ||
| + | return; | ||
| + | } | ||
| + | |||
| + | int k1 = (k + 1) / 2; | ||
| + | int k2 = k - k1; | ||
| + | |||
| + | // bisecting current graph | ||
| + | vector<int> sorted_idx1 = bisect(idx); | ||
| + | vector<int> sorted_idx2(make_move_iterator(sorted_idx1.begin() + k1 * sorted_idx1.size() / k), | ||
| + | make_move_iterator(sorted_idx1.end())); | ||
| + | sorted_idx1.erase(sorted_idx1.begin() + k1 * sorted_idx1.size() / k, sorted_idx1.end()); | ||
| + | |||
| + | recursive_bisection(sorted_idx1, k1); | ||
| + | recursive_bisection(sorted_idx2, k2); | ||
| + | } | ||
| + | |||
| + | int main() | ||
| + | { | ||
| + | // example: uniform MxN-mesh | ||
| + | for(size_t i = 0; i < N; ++i) | ||
| + | for(size_t j = 0; j < M; ++j) { | ||
| + | points_matrix[0][M * i + j] = i * STEP; | ||
| + | points_matrix[1][M * i + j] = j * STEP; | ||
| + | } | ||
| + | |||
| + | vector<int> idx(M * N); | ||
| + | iota(idx.begin(), idx.end(), 0); | ||
| + | |||
| + | recursive_bisection(idx, K); | ||
| + | |||
| + | // partitioning results | ||
| + | for(size_t i = 0; i < graph_partition.size(); ++i) { | ||
| + | for(size_t j = 0; j < graph_partition[i].size(); ++j) | ||
| + | cout << graph_partition[i][j] << " "; | ||
| + | cout << endl; | ||
| + | } | ||
| + | } | ||
| + | </source> | ||
| + | |||
== Локальность данных и вычислений == | == Локальность данных и вычислений == | ||
| Строка 138: | Строка 311: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| + | Эксперименты проводились на компьютере с четырехъядерным процессором Intel Core i7 3610QM 2300 Mhz, который поддерживает до 8 потоков и оперативной памятью типа DDR3 1600 МГц размером 8 Gb. | ||
| + | |||
| + | Набор и границы значений изменяемых [[Глоссарий#Параметры запуска|параметров запуска]] реализации алгоритма: | ||
| + | |||
| + | * число потоков от 1 до 8 с шагом 1; | ||
| + | * размер сетки N x N, n от 500 до 2000 с шагом 500; | ||
| + | * число доменов k 100 и от 2000 до 10000 с шагом 1000; | ||
| + | |||
| + | <center> | ||
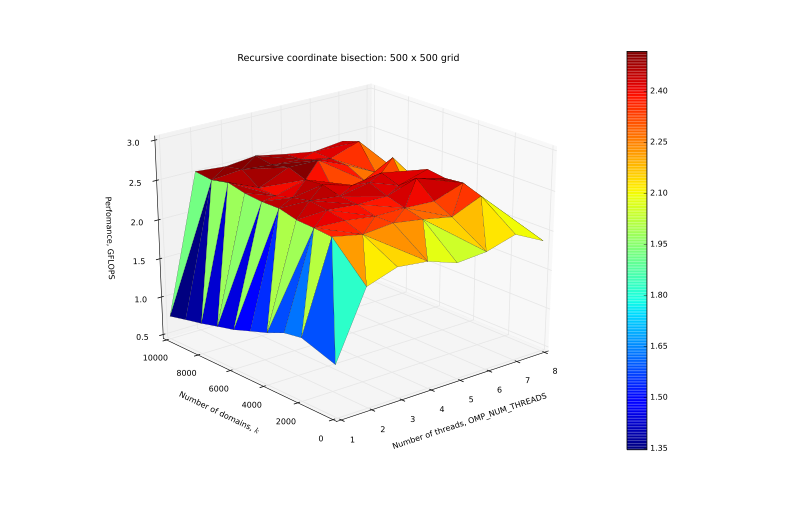
| + | [[Файл:Perf_500.svg|thumb|center|800px|Рисунок 2. График производительности на сетке 500 x 500.]] | ||
| + | </center> | ||
| + | |||
| + | <center> | ||
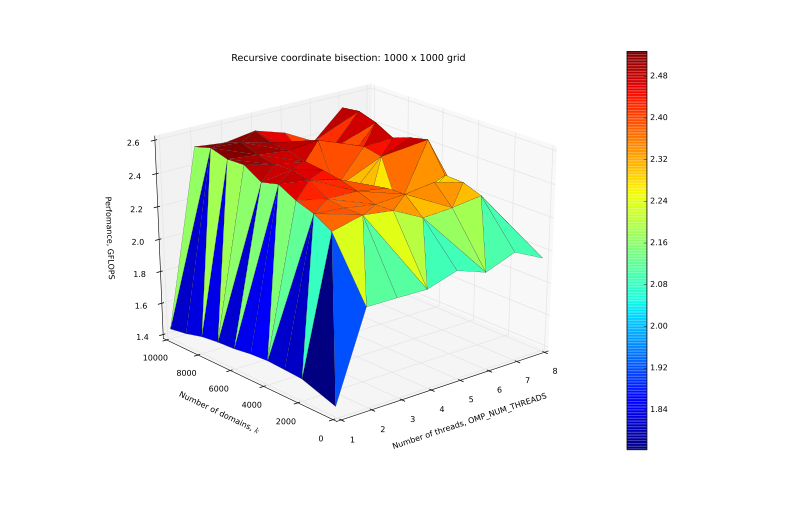
| + | [[Файл:Perf_1000.svg|thumb|center|800px|Рисунок 3. График производительности на сетке 1000 x 1000.]] | ||
| + | </center> | ||
| + | |||
| + | <center> | ||
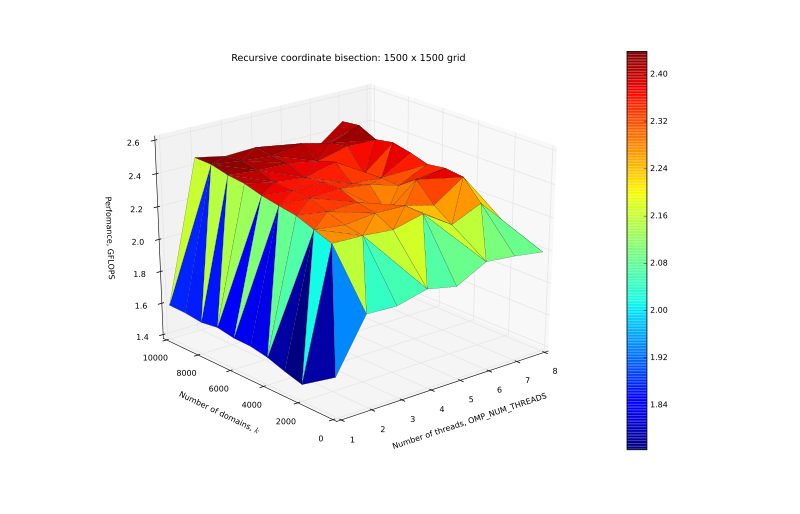
| + | [[Файл:Perf_1500.svg|thumb|center|800px|Рисунок 4. График производительности на сетке 1500 x 1500.]] | ||
| + | </center> | ||
| + | |||
| + | <center> | ||
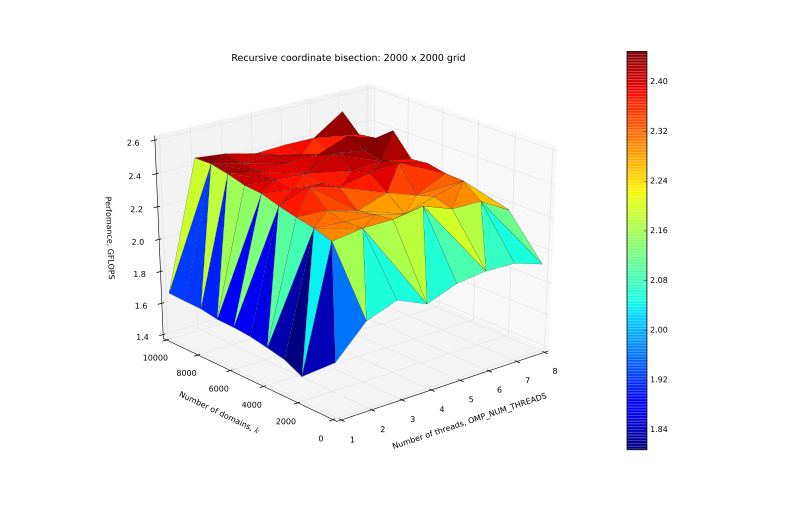
| + | [[Файл:Perf_2000.svg|thumb|center|800px|Рисунок 5. График производительности на сетке 2000 x 2000.]] | ||
| + | </center> | ||
| + | |||
| + | |||
| + | |||
| + | <center> | ||
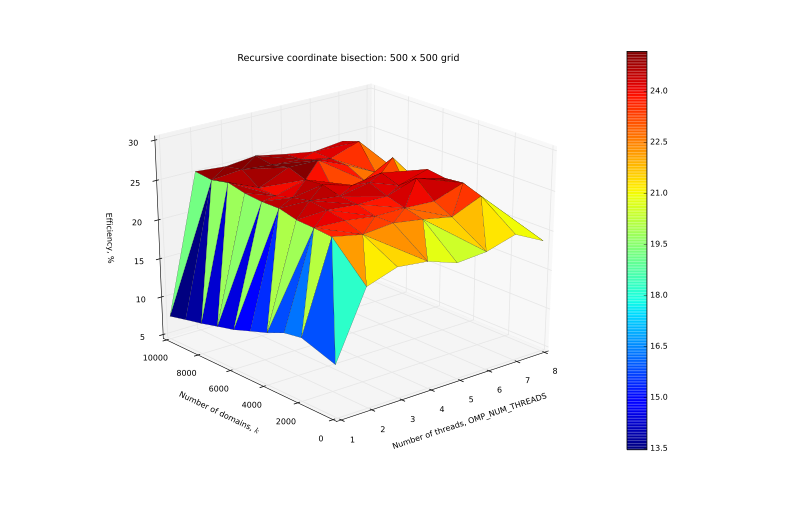
| + | [[Файл:Eff_500.svg|thumb|center|800px|Рисунок 6. График эффективности на сетке 500 x 500.]] | ||
| + | </center> | ||
| + | |||
| + | <center> | ||
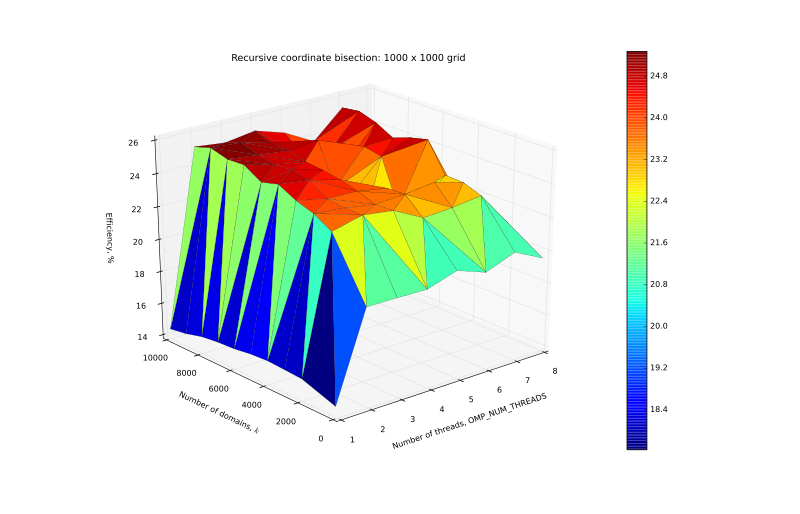
| + | [[Файл:Eff_1000.svg|thumb|center|800px|Рисунок 7. График эффективности на сетке 1000 x 1000.]] | ||
| + | </center> | ||
| + | |||
| + | <center> | ||
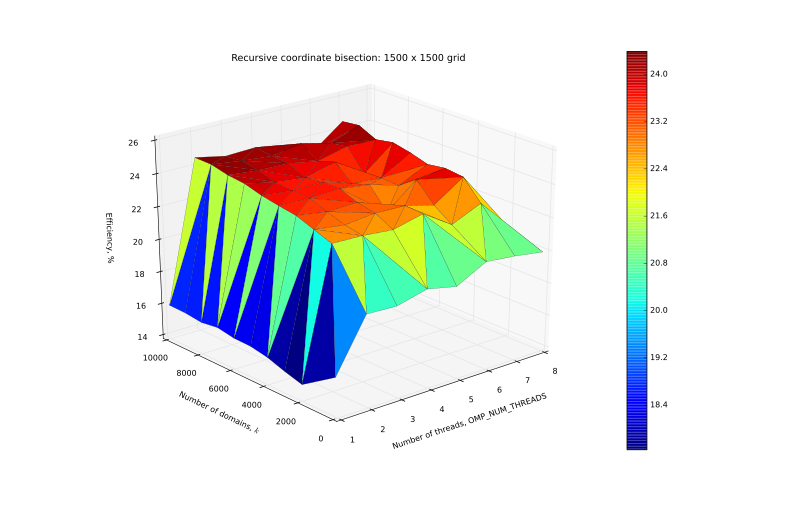
| + | [[Файл:Eff_1500.svg|thumb|center|800px|Рисунок 8. График эффективности на сетке 1500 x 1500.]] | ||
| + | </center> | ||
| + | |||
| + | <center> | ||
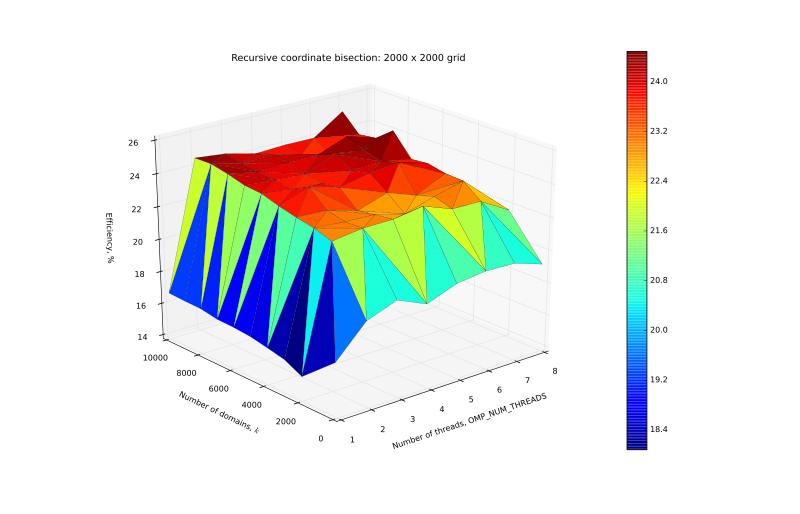
| + | [[Файл:Eff_2000.svg|thumb|center|800px|Рисунок 9. График эффективности на сетке 2000 x 2000.]] | ||
| + | </center> | ||
| + | |||
| + | [http://pastebin.com/hCqz7vBU Параллельная реализация алгоритма на языке C++] | ||
| + | |||
| + | В статье <ref>http://glaros.dtc.umn.edu/gkhome/node/112</ref> приводятся результаты работы алгоритма декомпозиции графов из пакета ParMETIS. В таблице ниже приведено время работы алгоритма в зависимости от числа вершин в графе и используемого числа процессоров. Рассмотравились следующие графы: | ||
| + | граф mrng2 с 1 миллионом вершин, mrng3 с 4 миллионами и граф mrgn4 с 7.5 миллионами вершин. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ Время выполнения разбиения графа с использованием Parmetis | ||
| + | |- | ||
| + | ! Graph | ||
| + | ! 8 processors | ||
| + | ! 16 processors | ||
| + | ! 32 processors | ||
| + | ! 64 processors | ||
| + | ! 128 processors | ||
| + | |- | ||
| + | | mrng2 | ||
| + | | 5.4 | ||
| + | | 3.1 | ||
| + | | 2.1 | ||
| + | | 1.5 | ||
| + | | 1.7 | ||
| + | |- | ||
| + | | mrng3 | ||
| + | | 15.8 | ||
| + | | 8.8 | ||
| + | | 4.8 | ||
| + | | 3.0 | ||
| + | | 2.7 | ||
| + | |- | ||
| + | | mrng4 | ||
| + | | 38.6 | ||
| + | | 16.2 | ||
| + | | 8.8 | ||
| + | | 5.0 | ||
| + | | 3.6 | ||
| + | |} | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
| Строка 153: | Строка 404: | ||
= Литература = | = Литература = | ||
| − | |||
| − | |||
[[en:Recursive coordinate bisection method]] | [[en:Recursive coordinate bisection method]] | ||
Текущая версия на 11:39, 29 ноября 2016
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 29.11.2016 Данная работа соответствует формальным критериям. Проверено Dan. |
| Рекурсивная координатная бисекция | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n \log_2{n} \log_2{k})[/math] |
| Объём входных данных | [math]N|V| + |G|[/math] |
| Объём выходных данных | [math]|V|[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]\log_2{k}[/math] |
| Ширина ярусно-параллельной формы | [math]k[/math] |
Авторы: Гордеев Михаил (разделы 1.4, 1.6, 1.8, 1.10, 2.1, 2.4), Колмаков Евгений (разделы 1.1, 1.2, 1.3, 1.5, 1.7, 1.9, 2.1, 2.4, 2.7).
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
1.1.1 Задача декомпозиции графа
Метод рекурсивной координатной бисекции является одним из методов, применяемых для декомпозиции графов [1]. В прикладных задачах, как правило, граф представляет собой сетку в пространстве некоторой размерности. При численном решении задач механики сплошной среды с помощью методов конечных разностей или конечных элементов широко используется геометрический параллелизм, при котором сетка, покрывающая расчётную область, разбивается на множество доменов, каждый из которых обрабатывается отдельным процессором. Основная проблема связана с необходимостью решения задачи статистической балансировки загрузки, то есть равномерного распределения вычислительной нагрузки между процессорами за счёт выбора оптимальной декомпозиции сетки.
1.1.2 Критерии декомпозиции
В зависимости от специфики решаемой задачи, к виду декомпозиции графов могут быть предъявлены разные требования. Существует много критериев декомпозиции, однако наиболее классическим из них считается минимизация максимального веса исходящих из домена ребёр (в простейшем случае - минимизация числа разрезанных ребер). Среди других критериев можно выделить следующие:
- выделение обособленных доменов;
- минимизация максимальной степени доменов;
- обеспечение связности доменов;
- обеспечение связности множества внутренних узлов доменов.
1.1.3 Метод рекурсивной бисекции
Метод рекурсивной координатной бисекции является частным случаем более общего метода рекурсивной бисекции. В этом методе сетка последовательно за [math]k-1[/math] шаг делится на [math]k[/math] частей. На первом шаге сетка делится на две части, далее каждая из полученных ранее частей также делится на две части и т.п. Конкретные алгоритмы деления сетки на две части (бисекции) и определяют метод рекурсивной бисекции. Соотношение размеров частей зависит количества доменов и процедуры вычисления желаемого числа вершин в каждой из формируемых частей графа.
1.1.4 Метод рекурсивной координатной бисекции
Для декомпозиции больших сеток применяют параллельные алгоритмы, предполагающие, что сетка уже распределена по процессорным узлам. Они эффективны, только если вершины распределены по процессорам компактными группами, а не произвольно. Однако к моменту начала работы алгоритмов декомпозиции, никакая декомпозиция сетки еще не найдена, поэтому требуется некоторый простой способ предварительного распределения графа по выполняющим декомпозицию процессорам. Для решения этой задачи и используется метод рекурсивной покоординатной бисекции. Несмотря на то, что он уступает по качеству формируемой декомпозиции некоторым другим методам, его целесообразно использовать на предварительном этапе, благодаря скорости работы, ориентированности на распределенную обработку и простоте.
Метод рекурсивной координатной бисекции основан на методе рекурсивной бисекции. Для разбиения сетки на две части используется следующая процедура:
- выбирается одна из координатных осей;
- множество вершин сортируется по этой координате;
- отсортированное множество разбивается на две части, то есть указывается индекс [math]i[/math] такой, что в первую часть попадают вершины с номерами меньшими либо равными [math]i[/math], а во вторую - оставшиеся вершины; геометрически это соответствует гиперплоскости, перпендикулярной выбранной оси, которая разбивает множество вершин сетки на две части, соотношение размеров которых зависит
1.1.5 Выбор координатной оси
В зависимости от критериев декомпозиции и других особенностей задачи могут быть использованы различные критерии выбора координатной оси вдоль, которой будет производится разбиение сетки на две части. Наиболее используемыми являются следующие:
- Протяжённость области вдоль данной оси: для каждой оси вычисляется разность между максимумом и минимумом координат вершин сетки по данной оси, и выбирается ось с наибольшим значением этой величины;
- Число разрезанных ребер при разбиении сетки вдоль данной оси: вершины упорядочиваются вдоль каждой из осей, и выбирается тот вариант, который приводит к наименьшему числу разрезанных ребер;
1.2 Математическое описание алгоритма
Исходные данные: граф [math]G = (V, E) [/math], вложенный в [math]\mathbb{R}^N[/math] (то есть каждая вершина этого графа - это точка в [math]N[/math] мерном пространстве), и число [math]k[/math] доменов, на которое нужно разбить граф. Под декомпозицией графа на [math]k[/math] доменов понимается разбиение множества вершин [math]V[/math] на [math]k[/math] подмножеств [math]V_1, \dots, V_k[/math] таких, что
С каждым доменом можно связать порождённый им подграф [math]G(V_i) = (V_i, E_i)[/math], где [math]E_i \subseteq E[/math] - множество рёбер, оба конца которых принадлежат домену.
Задача заключается в нахождении декомпозиции [math]V_1, \dots, V_k[/math], доставляющей минимум некоторого функционала (см. соответствующий пункт), например, числа разрезанных рёбер [math]E_{\mbox{cut}} = |\{(u, v) \in E \mid u \in V_i, v \in V_j, i \neq j\}| = |E| - \sum_{i = 1}^k |E_i|[/math].
Дадим формальное описание алгоритма. Как уже упоминалось, метод основан на алгоритме рекурсивной бисекции, поэтому представляет собой рекурсивную процедуру, на вход которой поступает граф [math]G = (V, E) [/math] и число доменов [math]k[/math], на которое нужно разбить множество вершин данного графа. Внутри этой процедуры выполняется следующая последовательность действий:
- в зависимости от числа доменов вычисляется "желаемое" число доменов и вершин в каждой из частей разбиения;
- вызывается процедура координатной бисекции для получения разбиения графа на две части;
- для каждой из двух полученных частей рекурсивно вызывается описываемая процедура (если число доменов для этой части больше единицы).
Процедура координатной бисекции устроена следующим образом:
- выбирается координатная ось [math]m^* \in \{1, \dots, N\}[/math];
- в случае максимизации протяженности: для каждой оси [math]m[/math] вычисляется величина [math]l_m = \max_{v \in V} v_m - \min_{v \in V} v_m[/math], и выбирается ось [math]m^* = \arg\max_{m \in \{1, \dots, N\}} l_m[/math];
- в случае минимизации числа разрезанных ребер: вершины упорядочиваются вдоль каждой из осей, для каждой оси вычисляется величина [math]E^m_{\mbox{cut}}[/math], равная числу разрезанных ребер при разбиении вдоль данной оси, и выбирается ось [math]m^* = \arg\max_{m \in \{1, \dots, N\}} E^m_{\mbox{cut}}[/math];
- множество вершин сортируется по возрастанию координаты с номером [math]m^*[/math];
- отсортированный массив вершин делится на две (непрерывные) части в соответствии с желаемым числом вершин в каждой из частей;
- как правило, выбирается индекс [math]i = \lfloor\frac{k+1}{2k}\rfloor \cdot |V|[/math], соответствующий примерно равному разделению текущего графа на части;
- первая часть состоит из вершин [math]v \in V[/math] с индексами [math]j \leqslant i[/math], вторая - с индексами [math]j \gt i[/math].
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма составляют сортировки массива вершин сетки по выбранной координате при каждом из [math]k - 1[/math] вызовов процедуры бисекции.
Также, в зависимости от критерия выбора координатной оси, требуются дополнительные вычисления:
- В случае максимизации протяженности при каждом вызове требуется вычисление величины [math]l_m[/math].
- В случае минимизации числа разрезанных ребер при каждом вызове требуется сортировка по каждой из координат (таким образом, при каждом разбиении осуществляется [math]N[/math] сортировок).
1.4 Макроструктура алгоритма
Как записано в описании ядра алгоритма, основную часть метода составляют множественные (всего [math]k-1[/math]) сортировки (функция argsort в коде в следующем разделе).
1.5 Схема реализации последовательного алгоритма
Опишем последовательную реализацию метода рекурсивной координатной бисекции, где выбор оси производится исходя из условия максимизации протяженности вдоль этой оси. Ниже представлен код данного алгоритма на языке Python 3.
# Переменная для хранения результата работы алгоритма
partition = []
# V - numpy.ndarray размера |V| x N, k - число доменов
def recursive_bisection(V, k):
global partition
# Если текущая часть графа есть домен, добавляем ее к результату разбиения
if (k <= 1):
partition.append(V)
return
# Вычисляем количество доменов в каждой из частей
k1 = (k + 1) / 2
k2 = k - k1
# Производим разбиение
V1, V2 = bisect(V, k)
# Рекурсивно разбиваем каждую из частей
recursive_bisect(V1, k1)
recursive_bisect(V2, k2)
def bisect(V, k):
# Вычисляем координату с наибольшей протяженностью
t = V.max(axis=0) - V.min(axis=0)
m = t.argmax()
# Сортируем вершины по координате с номером m
V_sorted = V[V[:, m].argsort()]
# Вычисляем индекс для разбиения в соответствии с числом доменов
ind = (k + 1) * V.shape[0] // (2 * k)
return V_sorted[:ind, :], V_sorted[ind:, :]
Приведённый код предназначен для более подробного описания основных шагов в алгоритме, представляет собой лишь схему и не является максимально эффективным. Это сделано для того, чтобы код был более наглядным. В более эффективной реализации, например, вместо создания массивов в процедуре bisect можно везде оперировать только индексами.
1.6 Последовательная сложность алгоритма
Обозначим через [math]D_k(n)[/math] сложность алгоритма рекурсивной координатной бисекции для декомпозиции графа с [math]n[/math] вершинами на [math]k[/math] доменов.
Определим величину [math]D(n) = D_n(n)[/math]. Для [math]D(n)[/math] имеет место следующее рекуррентное равенство:
[math] \begin{array}{l} D(n) = S(n) + 2D(\frac{n}{2}) \\ D(1) = S(1) = 0. \\ \end{array} [/math], где [math]S(n)[/math] - это сложность алгоритма сортировки массива из [math]n[/math] элементов.
Пусть [math]S(n) = O(n\log_2{n})[/math] (например, для сортировки слиянием), тогда по теореме о рекуррентных соотношениях [2] для произвольного положительного [math]\varepsilon[/math] имеет место оценка [math]D(n) \lesssim n^{1+\varepsilon}[/math].
Величину [math]D_k(n)[/math] можно явно посчитать по формуле [math]\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}2^i S(\frac{n}{2^i})[/math]. Если использовать сортировку со сложностью [math]S(n) = O(n\log_2{n})[/math], то
[math]D_k(n) = [/math] [math]O(\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}2^i \frac{n}{2^i} \log_2{\frac{n}{2^i}}) = [/math] [math]O(n\log_2(\prod\limits_{i=0}^{\lceil\log_2{k}\rceil}\frac{n}{2^i})) = [/math] [math]O(n\log_2{\frac{n^{\log_2{k}}}{2^\frac{\log_2{k}(\log_2{k}+1))}{2}}}) =[/math] [math] O(n(\log_2{n}\log_2{k} - \frac{\log^2_2{k}}{2})) = [/math] [math]O(n\log_2{n}\log_2{k})[/math].
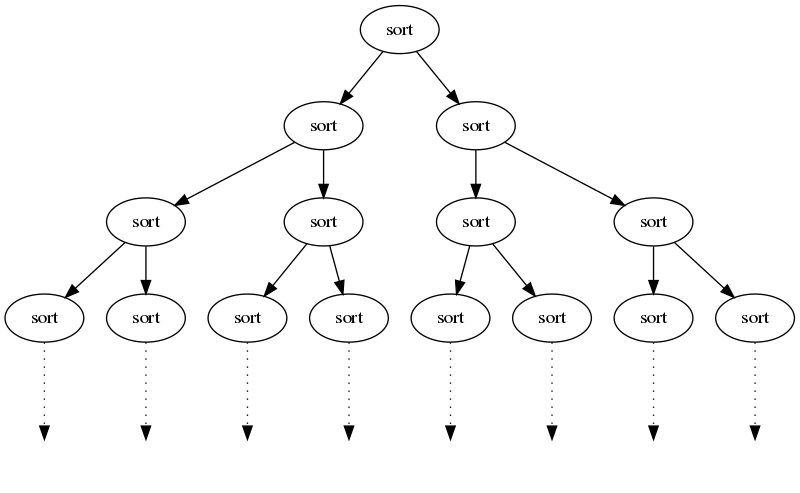
1.7 Информационный граф
Под операцией в данном пункте будем понимать макрооперацию сортировки. Передача данных происходит после разбиения множества вершин на две части. Таким образом, информационный граф представляет из себя бинарное дерево с [math]k[/math] листьями. На рисунке ниже приведена часть информационного графа для [math]k = 16[/math]. Зависимость от числа вершин [math]n[/math] учитывается в самих узлах дерева.
Высота ярусно-параллельной формы - [math]\log_2{k}[/math].
Ширина ярусно-параллельной формы - [math]k[/math].
Если рассматривать более мелкие операции, используемые в процессе сортировки, то глобально информационный граф будет выглядеть также, однако каждый узел будет заменён на информационный граф используемого алгоритма сортировки (или [math]N[/math] таких графов, если используется критерий минимизации числа разрезов).
1.8 Ресурс параллелизма алгоритма
Данный алгоритм обладает координатным параллелизмом. Для декомпозиции графа с [math]n[/math] вершинами на [math]k[/math] доменов методом рекурсивной координатной бисекции в параллельном варианте требуется последовательно выполнить [math]\lceil\log_2{k}\rceil[/math] ярусов. На [math]i[/math]-ом ярусе будет выполнятся [math]2^i[/math] операций сортировки. Рассмотрим два случая распараллеливания нашего алгоритма:
- Параллельное выполнение операций на каждом ярусе с использованием последовательного алгоритма сортировки со сложностью [math]O(n\log_2{n})[/math].
- На первом шаге один процессор производит сортировку всех вершин, разделяет граф на два подграфа и передает однин из подрафов новому процессору.
- На [math]i[/math]-ом шаге каждый из уже получивший свой граф процессор производит сортировку всех вершин, разделяет граф на два подграфа и передает однин из подрафов новому процессору.
Тогда сложность нашего алгоритма равна:
[math]D_k(n) = O(\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}\frac{n}{2^i} \log_2{\frac{n}{2^i}}) = [/math] [math]n\sum\limits_{i=0}^{\lceil\log_2{k}\rceil}(\frac{\log_2{n}}{2^i} - \frac{i}{2^i}) = [/math] [math]O(n\log_2{n}) - O(n) = O(n\log_2{n})[/math].
- Параллельное выполнение операций на каждом ярусе с использованием параллельного алгоритма сортировки со сложностью [math]O(\log_2^2{n})[/math][3].
На каждом шаге производится параллельная сортировка вершин и разбиение графа на два подграфа. В этом случае
[math]D_k(n) = \sum\limits_{i=0}^{\lceil\log_2{k}\rceil}\log^2_2\frac{n}{2^i} = O(\log^2_2{n}\log_2{k}) = O(\log^3_2{n})[/math].
Известно [4], что оптимальная параллельная сортировка имеет сложность [math]O(\log_2{n})[/math]. В этом случае
[math]D_k(n) = \sum\limits_{i=0}^{\lceil\log_2{k}\rceil}\log_2\frac{n}{2^i} = O(\log_2{n}\log_2{k})[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: граф [math]G = (V, E) [/math], вложенный в [math]\mathbb{R}^N[/math], и число [math]k[/math] частей (доменов), на которое нужно разбить граф. Таким образом, помимо матрицы смежности (или любого другого представления графа) для каждой вершины [math]v \in V[/math] задан набор её координат [math]v = (v_1, \dots, v_N) \in \mathbb{R}^N[/math], поэтому [math]V[/math] задаётся массивом [math]N[/math]-мерных векторов или матрицей размера [math]|V| \times N[/math].
Объём входных данных: [math]N|V| + |G|[/math], где [math]|G|[/math] - объём данных, представляющих граф [math]G[/math], который в общем случае зависит от выбранного представления.
Выходные данные: [math]k[/math] доменов графа [math]G[/math], задающих его декомпозицию.
Объём выходных данных: [math]|V|[/math] - для каждого домена достаточно хранить соответствующие вершинам из этого домена индексы строк в матрице, представляющей множество вершин.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейным (отношение [math]O(n\log{n})[/math] к [math]O(\log{n}))[/math].
Алгоритм детерминирован в случае использования устойчивой сортировки вершин. Также алгоритм устойчив, так как используются операции, не приводящие к ошибкам округления - это операции сравнения для вещественных чисел и операции с целыми числами. Наибольшее число операций составляют операции сравнения.
Так как количество вершин на разных процессорах примерно одинаковое алгоритм является сбалансированным по числу операций на каждом процессоре.
Алгоритм достаточно прост и легко модифицируется в зависимости от критерия декомпозиции.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Ниже приведен пример реализации последовательного алгоритма на языке C++. Следует отметить, что исходный массив вершин не изменяется, вся работа осуществляется с индексами.
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
#define N 5
#define M 5
#define STEP 0.01
#define N_DIMS 2
#define N_DOMAINS 6
vector<vector<double> > points_matrix(N_DIMS, vector<double>(N * M));
vector<vector<int> > graph_partition;
double span(vector<double> x, vector<int> idx)
{
double max_value = x[idx[0]];
double min_value = x[idx[0]];
for (size_t i = 1; i < idx.size(); i++) {
max_value = (x[idx[i]] > max_value) ? x[idx[i]] : max_value;
min_value = (x[idx[i]] < min_value) ? x[idx[i]] : min_value;
}
return max_value;
}
vector<int> bisect(vector<int> idx)
{
double max_span = 0;
double max_ind = 0;
// finding coordinate with maximal span
for (size_t i = 0; i < points_matrix.size(); i++) {
double cur_span = span(points_matrix[i], idx);
if (cur_span > max_span) {
max_span = cur_span;
max_ind = i;
}
}
// sorting vertices along this coordinate
sort(idx.begin(), idx.end(), [&](const int& a, const int& b) {
return points_matrix[max_ind][a] < points_matrix[max_ind][b];
});
return idx;
}
void recursive_bisection(vector<int> idx, int k)
{
// adding current domain to partition
if (k < 2) {
graph_partition.push_back(idx);
return;
}
int k1 = (k + 1) / 2;
int k2 = k - k1;
// bisecting current graph
vector<int> sorted_idx1 = bisect(idx);
vector<int> sorted_idx2(make_move_iterator(sorted_idx1.begin() + k1 * sorted_idx1.size() / k),
make_move_iterator(sorted_idx1.end()));
sorted_idx1.erase(sorted_idx1.begin() + k1 * sorted_idx1.size() / k, sorted_idx1.end());
recursive_bisection(sorted_idx1, k1);
recursive_bisection(sorted_idx2, k2);
}
int main()
{
// example: uniform MxN-mesh
for(size_t i = 0; i < N; ++i)
for(size_t j = 0; j < M; ++j) {
points_matrix[0][M * i + j] = i * STEP;
points_matrix[1][M * i + j] = j * STEP;
}
vector<int> idx(M * N);
iota(idx.begin(), idx.end(), 0);
recursive_bisection(idx, K);
// partitioning results
for(size_t i = 0; i < graph_partition.size(); ++i) {
for(size_t j = 0; j < graph_partition[i].size(); ++j)
cout << graph_partition[i][j] << " ";
cout << endl;
}
}
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Эксперименты проводились на компьютере с четырехъядерным процессором Intel Core i7 3610QM 2300 Mhz, который поддерживает до 8 потоков и оперативной памятью типа DDR3 1600 МГц размером 8 Gb.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число потоков от 1 до 8 с шагом 1;
- размер сетки N x N, n от 500 до 2000 с шагом 500;
- число доменов k 100 и от 2000 до 10000 с шагом 1000;
Параллельная реализация алгоритма на языке C++
В статье [5] приводятся результаты работы алгоритма декомпозиции графов из пакета ParMETIS. В таблице ниже приведено время работы алгоритма в зависимости от числа вершин в графе и используемого числа процессоров. Рассмотравились следующие графы: граф mrng2 с 1 миллионом вершин, mrng3 с 4 миллионами и граф mrgn4 с 7.5 миллионами вершин.
| Graph | 8 processors | 16 processors | 32 processors | 64 processors | 128 processors |
|---|---|---|---|---|---|
| mrng2 | 5.4 | 3.1 | 2.1 | 1.5 | 1.7 |
| mrng3 | 15.8 | 8.8 | 4.8 | 3.0 | 2.7 |
| mrng4 | 38.6 | 16.2 | 8.8 | 5.0 | 3.6 |
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Описанный алгоритм реализован во многих пакетах декомпозиции графов, включающих в себя и другие версии алгоритма бисекции.
Последовательная версия алгоритма реализована в пакетах Chaco, JOSTLE, METIS, SCOTCH.
Параллельная версия реализована в пакетах JOSTLE, ParMETIS, PT-SCOTCH.
Стоит отметить, что пакеты METIS и ParMETIS распространяются свободно.
3 Литература
- ↑ Якобовский М.В. Введение в параллельные методы решения задач: Учебное пособие / Предисл.: В. А. Садовничий. – М.: Издательство Московского университета, 2012. – 328 с., илл. – (Серия «Суперкомпьютерное образование»), ISBN 978-5-211-06382-2 URL: http://lira.imamod.ru/ITTPMOPS/
- ↑ https://ru.wikipedia.org/wiki/Основная_теорема_о_рекуррентных_соотношениях
- ↑ https://en.wikipedia.org/wiki/Batcher_odd–even_mergesort
- ↑ https://en.wikipedia.org/wiki/Sorting_algorithm
- ↑ http://glaros.dtc.umn.edu/gkhome/node/112