Участник:KibAndrey/Ортогонализация Грама-Шмидта

Ортогонализация Грама-Шмидта
Последовательный алгоритм
Последовательная сложность	[math]O\left(k^2n\right)[/math]
Объём входных данных	[math]kn[/math]
Объём выходных данных	[math]kn[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(k\log{n})[/math]
Ширина ярусно-параллельной формы	[math]O(kn)[/math]

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 21.10.2016 Авторы этой статьи считают, что задание выполнено.

Основные авторы описания: [[Участник:KibAndrey| А.В.Кибанов], Т.З.Аджиева. Все пункты данной статьи обсуждались и создавались совместно, доля ответственности равноправна.

1 ЧАСТЬ. Свойства и структура алгоритма

1.1 Общее описание алгоритма

Процесс ортогонализации Грама–Шмидта — алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства [math]V[/math] ортогональной системы ненулевых векторов, при котором каждый вектор построенной системы линейно выражается через векторы данной системы.

Исторически это первый алгоритм, описывающий процесс ортогониализации. Традиционно его связывают с именами Йоргена Педерсена Грама и Эрхарда Шмидта. Йорган Педерсен Грам был датским актуарием, который в неявном виде представил суть процесса ортогонализации в 1883 году. Нельзя не сказать о том, что метод ортогонализации в несколько ином, модифицированом виде, ранее использовал Пьер-Симон Лаплас при нахождении массы Сатурна и Юпитера из систем нормальных уравнений и расчете распределения ошибок при этих вычислениях. Ясно, что Й. Грам не знал о том, что Лаплас ранее использовал этот метод. Эрхард Шмидт был учеником великих математиков Германа Шварца и Давида Гильберта. Алгоритм ортогонализации был опубликован Э. Шмидтом в 1907 году в его исследовании интегральных уравнений, которое в свою очередь дало основание для развития теории гильбертовых пространств. Шмидт использовал процесс ортогонализации применительно к геометрии гильбертова пространства решений интегральных уравнений отмечал, что процесс ортогонализации принципиально такой же, какой прежде использовал Й. Грам. В отечественной литературе иногда этот процесс называют ортогонализацией Сонина–Шмидта. Это название связано с тем, что разработанный Сониным метод ортогонализации системы функций для частного случая по существу не отличается от метода ортогонализации системы функций, предложенного ранее Шмидтом.

1.2 Математическое описание алгоритма

Bходные данные: [math]k[/math] линейно независимых векторов [math]\mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a_k}[/math] длины [math]n[/math] [math]\left(\alpha_{ij}\right.[/math], [math]j=1,2, \ldots,n[/math], — координаты вектора [math]\left.\mathbf{a_i}\right)[/math] .

Вычисляемые данные:

[math]k[/math] ортогональных векторов [math]\mathbf{b_1},\mathbf{b_2},...,\mathbf{b_k}[/math] длины [math]n[/math], причем [math]\mathbf{b_1}=\mathbf{a_1}[/math], либо

[math]k[/math] ортонормированных векторов [math]\mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k}[/math] длины [math]n[/math], причем [math]\mathbf{q_i}=\frac{\mathbf{b_i}}{|\mathbf{b_i}|}[/math], [math]i=1,2, \ldots,k[/math].

Формулы процесса ортогонализации:

[math] \begin{align} \mathbf{b_{1}} & =\mathbf{a_{1}}, \\ \mathbf{b_{2}}& =\mathbf{a_{2}}-\mathbf{b_{1}} proj_{\mathbf{b_1}}\mathbf{a_{2}}, \\ & ...\\ \mathbf{b_{i}} & =\mathbf{ a_{i}}-\sum\limits_{j=1}^{i-1}\mathbf{b_{i}} proj_{\mathbf{b_j}}\mathbf{a_{i}}.\\ & ...\\ \mathbf{b_{k}} & =\mathbf{ a_{k}}-\sum\limits_{j=1}^{k-1}\mathbf{b_{k}} proj_{\mathbf{b_j}}\mathbf{a_{k}}.\\ \end{align} [/math]

Здесь [math]proj_{\mathbf{b_j}}\mathbf{a_{i}}[/math], для [math]j=1,...,i-1[/math] — это число, равное по величине проекции вектора [math]\mathbf{a_{j}}[/math] на ось, проходящую через вектор [math]\mathbf{b_j}[/math].

Формула для ее вычисления, полученная из определения скалярного произведения: [math]proj_{\mathbf{b_j}}\mathbf{a_{i}}=\dfrac{(ai,bj)}{\mathbf{\left \|b_j\right \|}}[/math], для [math]j=1,...,i-1[/math]

Произведение длин [math]\mathbf{|b_1|},\mathbf{|b_2|},\ldots ,\mathbf{|b_k|}[/math] равно объему параллелепипеда, построенного на векторах системы [math]\left\{\mathbf{a_i}\right\}[/math], [math]i=1,2,\ldots ,k[/math], как на ребрах.

Явное выражение векторов [math]\mathbf{b_i}[/math] для [math]i=1,...,k[/math] через [math]\mathbf{a_1},\mathbf{a_2},...,\mathbf{a_k}[/math] дает формула

[math] \mathbf{b_i}= \begin{vmatrix} (a_1,a_1) & \cdots & (a_1,a_i-1) &a_1 \\ (a_{2},a_1) & \cdots & (a_2,a_i-1) &a_2 \\ \cdots & \cdots & \cdots& \cdots \\ (a_{i},a_1) & \cdots & (a_i,a_i-1) &a_i \\ \end{vmatrix} [/math]. (В правой части этого равенства определитель следует формально разложить по последнему столбцу).

Иногда полученные векторы нормируются сразу после их нахождения и находится система ортонормированных векторов [math]\mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k}[/math]. В этом случае знаменатель в формуле для вычисления проекции [math]|\mathbf{q_i}|=1[/math] для [math]i=1,...,k-1[/math], что существенно упрощает вычисления алгоритма. В настоящей статье применяя процесс ортогонализации к системе линейно независимых векторов, мы так и будем поступать.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит из вычисления:

• [math]\dfrac{k(k+1)}{2}[/math] [[Скалярное произведение векторов, вещественная версия, последовательный вариант| скалярных произведений] векторов

(включая нахождения скалярных произведений одинаковых векторов дальнейшего нахождения их длин);

• [math]\dfrac{(k-1)k}{2}[/math] умножений векторов на число после вычисления нового базисного вектора на итерации.

1.4 Макроструктура алгоритма

В уже отмечено описании вычислительного ядра алгоритма, основную часть метода составляют вычисления скалярных произведений, как для вычислении длины очередного вектора так и для расчета проекций прочих векторов на новый вектор, а также умножения векторов на числа, используемые при корректировке значений остальных векторов после вычисления очередного вектора, ортогонального предыдущим.

1.5 Схема реализации последовательного алгоритма

Входные данные: [math]k[/math] линейно независимых векторов [math]\mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a_k}[/math] длины [math]n[/math] [math]\left(\alpha_{ij}\right.[/math], где [math]j=1,2, \ldots,n[/math] — координаты вектора [math]\mathbf{a_i}[/math], для [math]\left.i=1,2, \ldots,k\right)[/math].

Вычисляемые данные:

[math]k[/math] ортогональных векторов [math]\mathbf{b_1},\mathbf{b_2},...,\mathbf{b_k}[/math] длины [math]n[/math] [math]\left(\beta_{ij}\right.[/math], где [math]j=1,2, \ldots,n[/math] — координаты вектора [math]\mathbf{b_i}[/math], для [math]\left.i=1,2, \ldots,k\right)[/math], причем [math]\mathbf{b_1}=\mathbf{a_1}[/math], либо

[math]k[/math] ортонормированных векторов [math]\mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k}[/math] длины [math]n[/math] ([math]\gamma_{ij}[/math], [math]j=1,2, \ldots,n[/math] — координаты вектора [math]\mathbf{q_i}[/math], для [math]\left.i=1,2, \ldots,k\right)[/math], причем [math]\mathbf{q_1}=\frac{\mathbf{b_i}}{|\mathbf{b_i}|}[/math], для [math]i=1,2, \ldots,k[/math].

Последовательность исполнения метода:

1. [math]len(a_1)=\sqrt{\alpha_{11}^2+\alpha_{12}^2+\ldots+\alpha_{1n}^2}[/math].

2. При [math]i[/math] от [math]1[/math] до [math]n[/math]:

[math]\gamma_{1j}= \frac{\alpha_{1j}}{len(a_1)}[/math].

3. При [math]i[/math] от [math]2[/math] до [math]k[/math]:

при [math]j[/math] от [math]1[/math] до [math]n[/math]:

[math]\beta_{ij}=\alpha_{ij}-\sum\limits_{k=1}^{j-1}\left(\sum\limits_{m=1}^n \alpha_{im}\gamma_{km}\right)\gamma_{kj} [/math]

[math]len(b_i)=\sqrt{\beta_{i1}^2+\beta_{i2}^2+\ldots+\beta_{in}^2}[/math]

при [math]j[/math] от [math]1[/math] до [math]n[/math]:

[math]\gamma_{ij}= \frac{\beta_{ij}}{len(b_{i})}[/math].

1.6 Последовательная сложность алгоритма

Для ортогонализации [math]n[/math] линейно независимых векторов длины [math]n[/math] в последовательном варианте с помощью классического метода ортогонализации Грама-Шмидта потребуется:

• [math]k[/math] вычислений квадратного корня
• [math]\frac{k(k-1)(n-1)}{2}[/math] сложений,
• [math]\frac{k(k-1)(n-1)}{2}[/math] вычитаний,
• [math]k^2 n[/math] умножений,
• [math]k[/math] делений.

Умножения, сложения и вычитания составляют основную часть алгоритма.

При классификации по последовательной сложности, таким образом, метода ортогонализации Грама-Шмидта с кубической сложностью.

1.7 Информационный граф

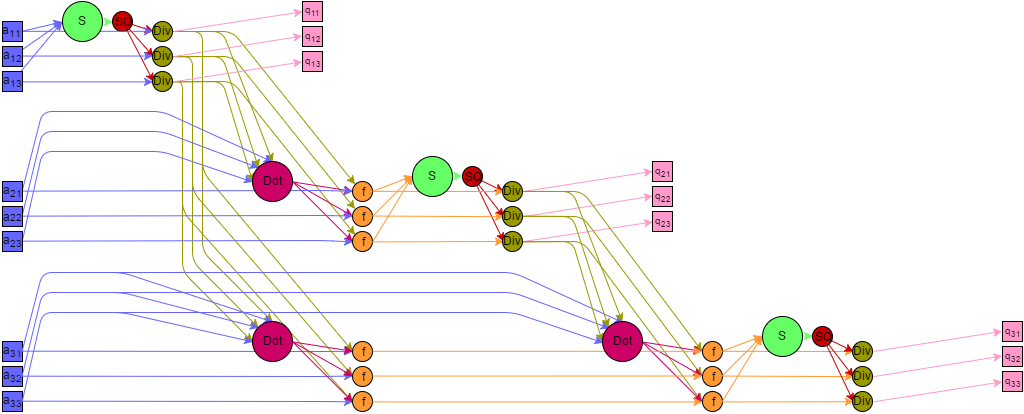
Представим граф алгоритма с помощью текстового описания, а также с помощью изображения.

Все вершины графа можно разбить на шесть групп, каждой из которых соответствует вид исполняемой операции. Каждая вершина расположена в точках с целочисленными координатами, в пространствах с числом измерений от [math]1[/math] до [math]4[/math]. Дадим описание каждой из групп.

Первая группа — вершины, которым соответствует операция возведение в квадрат. На графе они располагаются в двумерной области. [math]i[/math] изменяется от [math]1[/math] до [math]k[/math], [math]p[/math] изменяется от [math]1[/math] до [math]n[/math].

Значениями аргументов для этих функций являются:

• при [math]i = 1[/math] — входные данные [math]a_{1p}[/math];
• при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,1,\mathbf{p}[/math].

Результат этих операций является промежуточным данным алгоритма.

Вторая группа — вершины соответствующие операции сложения, которые проще разбить на две подгруппы, соответствующие четным и нечетным индексам. Они располагаются в четырехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]2k-1[/math], [math]j[/math] равно [math]1[/math] для нечетных [math]i[/math] и изменяется от [math]2[/math] до [math]k+1-\left\lceil{\dfrac{i}{2}}\right\rceil[/math] для четных [math]i[/math], [math]p[/math] изменяется от [math]1[/math] до [math]\left\lceil{\dfrac{n}{2^{i}}}\right\rceil[/math], [math]t[/math] изменяется от [math]1[/math] до [math]T = \left\lceil{\log_{2}(p)}\right\rceil[/math].

Значениями аргументов для этих функций являются:

• при [math]j = 1, t = 1[/math] — результат выполнения функций в вершинах первой группы с координатами [math](i+1)/2,1,2p[/math] и [math](i+1)/2,1,2p - 1[/math];
• при [math]j \gt 1, t = 1[/math] — результат выполнения функции в вершинах пятой группы с координатами [math]i/2,j-1,2p[/math] и [math]i,j-1,2p - 1[/math];
• при [math]t \gt 1[/math] — результат выполнения функций в вершинах второй группы с координатами [math]i,j,2p,t-1[/math] и [math]i,j,2p-1,t-1[/math] (это точно верно для случаев p являющихся степенью двойки. Для остальных вариантов аргументом может являться результат выполнения функций в вершинах второй группы с последней координатой меньшей чем [math]t-1[/math]).

Результат этих операций является промежуточным данным алгоритма.

Третья группа — вершины, которым соответствует операция SQRT извлечения квадратного корня. Они расположены в одномерной области, [math]i [/math] изменяется от [math]1[/math] до [math]k[/math]. Значением аргумента для этих функций является результат выполнения функции в вершине второй группы, с координатами [math]i,1,1,T[/math]

Результат является промежуточным данным алгоритма

Четвертая группа – вершины, которым соответствует операция деления. Располагаются в двумерной области, [math]i[/math] изменяется от [math]1[/math] до [math]k[/math], [math]p[/math] изменяется от [math]1[/math] до [math]n[/math]. Значениями аргументов для этих функций являются:

• делимое:
  • при [math]i = 1[/math] — входные данные [math]a_{1p}[/math];
  • при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,1,p[/math];
• делитель - результат выполнения функции в вершине третьей группы с координатой [math]i[/math]

Результат является выходным данным алгоритма [math]q_{ip}[/math]

Пятая группа — вершины, которым соответствует операция [math]a*b[/math]. Располагаются в трехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]k-1[/math], [math]j[/math] изменяется от [math]1[/math] до [math]k-i[/math], [math]p[/math] изменяется от [math]1[/math] до [math]n[/math]. Значениями аргументов для этих функций являются:

• [math]a[/math]:
  • при [math]i = 1[/math] — входные данные [math]a_{1+j,p}[/math];
  • при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,j+1,p[/math];
• [math]b[/math] — результат выполнения функции в вершине четвертой группы с координатой [math]i[/math]

Результат является промежуточным данным алгоритма

Шестая группа – вершины которые соответствуют операции [math]a - b*c[/math]. Располагаются в трехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]k-1[/math], [math]j[/math] изменяется от [math]1[/math] до [math]k-i[/math], [math]p[/math] изменяется от [math]1[/math] до [math]n[/math]. Значениями аргументов для этих функций являются:

• [math]a[/math]:
  • при [math]i = 1[/math] — входные данные [math]a_{1+j,p}[/math];
  • при [math]i \gt 1[/math] — результат выполнения функции в вершине шестой группы с координатами [math]i-1,j+1,p[/math];
• [math]b[/math] — результат выполнения функции в вершине второй группы, с координатами [math]i,j+1,1,T[/math]
• [math]c[/math] — результат выполнения функции в вершине четвертой группы с координатой [math]i[/math]

Результат является промежуточным данным алгоритма.

Описанный граф для случая [math]k = 3[/math], [math]n = 4[/math] изображен на рисунке. Каждая группа вершин отличается цветом и буквенным обозначением. "S" — первая группа, "+" — вторая группа, "SQ" — третья группа, "Div" — четвертая группа, "M" — пятая группа, "f" — шестая группа. Квадратные метки "In" и "out" обозначают передачу входных и выходных данных соответственно.

Рисунок 1. Граф алгоритма с отображением входных и выходных данных

1.8 Ресурс параллелизма алгоритма

Для построения ортонормированного базиса методом Грама–Шмидта необходимо выполнить следующие ярусы операций:

• [math]k[/math] ярусов вычисления квадратов числа (по [math]n[/math] операций на каждом);
• [math](2k-1)\left(\left\lceil{\log_{2}(n)}\right\rceil\right)[/math] ярусов суммирования (от [math]1[/math] до [math]\;(k-1)\cdot\dfrac{n}{2}\;[/math] операций на каждом);
• [math]k[/math] ярусов вычисления квадратного корня (по одной операции на каждом);
• [math]k[/math] ярусов деления( по [math]k[/math] операций на каждом);
• [math]k-1[/math] ярус умножения пары чисел (от [math]n[/math] до [math](k-1)n[/math] операций на каждом);
• [math]k-1[/math] ярус умножения/вычитания чисел (от [math]n[/math] до [math](k-1)n[/math] операций на каждом).

В этом случае сложность алгоритма при классификации по высоте ЯПФ — [math]O(k\log{n})[/math], при классификации по ширине ЯПФ — [math]O(kn)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: матрица [math]A[/math] с элементами [math]\alpha_{ij}[/math], где [math]i[/math] принимает значения [math]1,\ldots,k[/math], [math]j[/math] принимает значения [math] 1,\ldots,n[/math]. Здесь [math]k\leqslant n[/math]. По строкам этой матрицы записаны [math]k[/math] линейно-независимых векторов некоторого пространства размерности [math]n[/math].

Объем входных данных: [math]kn[/math].

Выходные данные: матрица [math]Q[/math] с элементами [math]\gamma_{ij}[/math]. Строки этой матрицы также задают [math]k[/math] векторов единичной длины размерности [math]n[/math], причем всякое скалярное произведение двух различных векторов этой системы равно [math]0[/math].

Объем выходных данных: [math]kn[/math].

Замечание: Алгоритм может работать с вырожденной матрицей, он выдаёт нулевую строку на шаге [math]j[/math], если строка [math]j[/math] матрицы [math]A[/math] является линейной комбинацией предыдущих строк. В этом случае для корректного продолжения работы алгоритма необходима дополнительная проверка на равенство строки нулю и пропуск соответствующих строк. Количество построенных векторов будет равняться размерности пространства, порождаемого строками матрицы.

1.10 Свойства алгоритма

Отношение последовательной и параллельной сложности алгоритма в случае неограниченных ресурсов равно [math]\dfrac{k^2n}{k\log{n}}=\dfrac{kn}{\log{n}}[/math]. Вычислительная мощность алгоритма линейная.

Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления.

Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов.

Большинство дуг информационного графа являются локальными. Исключение составляют дуги исходящие из операций деления и извлечения корня — для первой группы количество дуг пропорционально квадрату количества векторов, а для второй — пропорционально размерности пространства, в котором заданы эти вектора. Возникающие при это длинные дуги могут быть заменены несколькими короткими пересылками между соседями.

2 ЧАСТЬ Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Срок сдачи продлён до 15-го ноября.

2.7 Существующие реализации алгоритма

Для классического метода ортогонализации Грама–Шмидта существуют реализации в математических программных пакетах, таких как Matlab, Maxima, Mathematica. Также метод реализован в библиотеке SpectralPython для языка Python. Для устранения проблемы ошибок численных округлений иногда используется повторное применение метода к уже построенному ортогональному базису.

Поскольку метод ортогонализации Грама–Шмидта гарантирует получение [math]j[/math] ортогональных векторов к концу шага [math]j[/math], а не в самом конце работы алгоритма, используется в итерационных методах, таких как метод Арнольди. Для поддержки работы этого метода реализация ортогонализации Грама-Шмидта включена в библиотеку ARPACK.