Участник:Blizn/Хранение ненулевых элементов разреженной матрицы. Умножение разреженной матрицы на вектор.

Умножение разреженной матрицы на вектор
Последовательный алгоритм
Последовательная сложность	[math]O(l)[/math]
Объём входных данных	[math]2l+m+n+1[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(m)[/math]
Ширина ярусно-параллельной формы	[math]O(n)[/math]

Выполнила: И.В. Близнякова (611 группа).

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Разрежённая матрица — это матрица с преимущественно нулевыми элементами. В противном случае, если бо́льшая часть элементов матрицы ненулевые, матрица считается плотной.

Среди специалистов нет единства в определении того, какое именно количество ненулевых элементов делает матрицу разрежённой. Разные авторы предлагают различные варианты. Для матрицы порядка n число ненулевых элементов:

• есть [math]O(n)[/math]. Такое определение подходит разве что для теоретического анализа асимптотических свойств матричных алгоритмов;
• в каждой строке не превышает 10 в типичном случае;
• ограничено [math]n^{1+\gamma}[/math], где [math]\gamma \lt 1[/math].
• таково, что для данного алгоритма и вычислительной системы имеет смысл извлекать выгоду из наличия в ней нулей.

1.1.1 Хранение разреженной матрицы

1.1.1.1 Формат RR(C)O

Рассмотрим сначала формат RR(C)O. Сокращенное название данного формата происходит от английского словосочетания "Row - wise Representation Complete and Ordered" (строчное представление, полное и упорядоченное). В данном формате вместо одного двумерного массива, используются три одномерных. Значения ненулевых элементов матрицы и соответствующие им столбцовые индексы хранятся в этом формате по строкам в двух массивах [math]AN[/math] и [math]JA[/math]. Массив указателей [math]IA[/math], используется для ссылки на компоненты массивов [math]AN[/math] и [math]JA[/math], с которых начинается описание очередной строки. Последняя компонента массива [math]IA[/math] содержит указатель первой свободной компоненты в массивах [math]AN[/math] и [math]JA[/math], т.е. равна числу ненулевых элементов матрицы, увеличенному на единицу. Здесь уместно привести пример.

Рассмотрим матрицу [math]A[/math]:

[math]\begin{pmatrix} 0 & 0 & 0 & 2 & 0 \\ 1 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 6 & 0 & 0 & 0 \\ 0 & 0 & 4 & 0 & 0 \\ \end{pmatrix}[/math],

тогда ее представление в формате RR(C)O будет иметь вид:

  IA = [ 1 2 4 4 5 6 ]
  JA = [ 4 1 3 2 3 ]
  AN = [ 2 1 3 6 4 ]

Т.е. массив [math]AN[/math] содержит все не нулевые элементы исходной матрицы [math]A[/math], массив [math]JA[/math] номер столбца в котором находится соответствующий элемент из [math]AN[/math] и наконец массив [math]IA[/math] содержит номер с которого начинается описание элементов в массивах [math]JA[/math] и [math]AN[/math]. Таким образом информация об элементах 2-ой строки матрицы хранится в элементах с [math]IA[2] = 2[/math] по [math]IA[3] - 1 = 3[/math] включительно массивов [math]JA[/math] и [math]AN[/math]. Можно обратить внимание, что [math]IA[3] = IA[4] = 4[/math], а это означает, что 3-я строка матрицы [math]A[/math] нулевая.

В общем случае описание [math]r[/math]-й строки матрицы A хранится в компонентах с [math]IA[r][/math] до [math]IA[r + 1] - 1[/math] включительно массивов [math]AN[/math] и [math]JA[/math]. Если [math]IA[r + 1] = IA[r][/math], то это означает, что [math]r[/math]-я строка нулевая. Количество элементов в массиве [math]IA[/math] на единицу больше, чем число строк исходной матрицы, а количество элементов в массивах [math]JA[/math] и [math]AN[/math] равно числу ненулевых элементов исходной матрицы.

Данный способ представления называют полным, поскольку представлена вся матрица [math]A[/math], упорядоченным, поскольку элементы каждой строки матрицы [math]A[/math] хранятся в соответствии с возрастанием столбцовых индексов, и строчным, поскольку информация о матрице [math]A[/math] указывается по строкам.

Массивы [math]IA[/math] и [math]JA[/math] представляют портрет (структуру) матрицы [math]A[/math], задаваемый как множество списков смежности ассоциированного с [math]A[/math] графа. Если алгоритм, реализующий какую-либо операцию над разреженными матрицами, разбит на этапы символической обработки, на котором определяется портрет результирующей матрицы, и численной обработки, на котором определяются значения элементов результирующей матрицы, то массивы [math]IA[/math] и [math]JA[/math] заполняются на первом этапе, а массив [math]AN[/math] - на втором.

1.1.1.2 Формат RR(C)U

Рассмотрим теперь формат RR(C)U.

Сокращенное название данного формата происходит от английского словосочетания "Row - wise Representation Complete and Unordered" (строчное представление, полное, но неупорядоченное). Формат RR(C)U отличается от RR(C)O тем, что в данном случае соблюдается упорядоченность строк, но внутри каждой строки элементы исходных матриц могут храниться в произвольном порядке. Для матрицы [math]A[/math] нашего примера вполне можно было бы использовать и строчное представление, полное, но неупорядоченное такое:

  IA = [ 1 2 4 4 5 6 ]
  JA = [ 4 3 1 2 3 ]
  AN = [ 2 1 3 6 4 ]

Такие неупорядоченные представления могут быть очень удобны в практических вычислениях. Результаты большинства матричных операций получаются неупорядоченными, а их упорядочение стоило бы значительных затрат машинного времени. В то же время, за немногими исключениями, алгоритмы для разреженных матриц не требуют, чтобы их представления были упорядоченными.

1.1.1.3 Замечания

Несколько замечаний по поводу рассмотренных форматов представления:

1. Очевидно, что представление матрицы в формате RR(C)O так же является и представлением в формате RR(C)U, но не наоборот.
2. Из представления матрицы в формате RR(C) нельзя получить информацию о точном количестве столбцов исходной матрицы.
3. Целесообразно (в вопросе экономии памяти) использовать представления RR(C) в случае, если матрица содержит значительное число нулевых элементов.

1.1.2 Умножение разреженной матрицы на вектор

Важным приложением этих алгоритмов является вычисление векторов Ланцоша, необходимое при итерационном решении линейных уравнений методом сопряженных градиентов, а также при вычислении собственных значений и собственных векторов матрицы. Достоинство этих процедур, с вычислительной точки зрения, состоит в том, что единственная требуемая матричная операция - это повторное умножение матрицы на последовательность заполненных векторов; сама матрица не меняется.

Мы рассмотрим умножение разреженной матрицы общего вида, хранимой в форме RR(C)U посредством массивов [math]IA[/math], [math]JA[/math], [math]AN[/math] на заполненный вектор-столбец.

1.2 Математическое описание алгоритма

Исходные данные: разреженная матрица общего вида [math]A[/math] с элементами [math]a_{ij}[/math] ([math]i = 1,...,n[/math] и [math]j = 1,...,m[/math]). Заполненный вектор-столбец [math]b[/math] с элементами [math]b_{j}[/math] ([math]j =1,...,m[/math]).

Вычисляемые данные: заполненный вектор-столбец [math]c[/math] с элементами [math]c_{i}[/math] ([math]i = 1,...,n[/math]).

Формулы метода:

[math]c_{i} = \sum\limits_{k = 1}^{l_{i}} a_{i,j=j(k)}b_{j=j(k)}[/math],

где [math]l_{i}[/math] - количество ненулевых элементов строки [math]i[/math] матрицы [math]A[/math], [math]j(k)[/math] - индекс [math]k[/math]-го ненулевого элемента матрицы [math]A[/math].

1.3 Вычислительное ядро алгоритма

Вычислительное ядро последовательной версии умножения разреженной матрицы на вектор можно составить из множественных (всего их [math]n[/math]) вычислений скалярных произведений строк матрицы:

[math]c_{i} = \sum\limits_{k = 1}^{l_{i}} a_{i,j=j(k)}b_{j=j(k)}[/math].

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют множественные (всего [math]n[/math]) вычисления сумм:

[math]c_{i} = \sum\limits_{k = 1}^{l_{i}} a_{i,j=j(k)}b_{j=j(k)}[/math].

1.5 Схема реализации последовательного алгоритма

Далее предполагаем, что разреженная матрица общего вида [math]A[/math] хранится в форме RR(C)U посредством массивов [math]IA[/math], [math]JA[/math], [math]AN[/math]. Последовательность исполнения метода следующая:

Выполнять для [math]i[/math] от [math]1[/math] до [math]n[/math]

1. [math]c_{i} = 0[/math]
2. [math]IAA = IA[i][/math]
3. [math]IAB = IA[i + 1] - 1[/math]
4. [math]c_{i} = \sum\limits_{k = IAA}^{IAB} AN[k]b_{JA[k]}[/math].

После этого (если [math]i \le n[/math]) происходит переход к шагу 1 с бо́льшим [math]i[/math].

1.6 Последовательная сложность алгоритма

Для умножения разреженной матрицы общего вида, хранимой в форме RR(C)U, размером [math]n \times m[/math] на заполненный вектор [math]m \times 1[/math] в последовательном (наиболее быстром) варианте требуется:

• [math]l[/math] сложений,
• [math]l[/math] умножений.

Умножения и сложения составляют основную часть алгоритма.

При классификации по последовательной сложности, таким образом, алгоритм умножения разреженной матрицы на вектор относится к алгоритмам [math]O(l)[/math].

1.7 Информационный граф

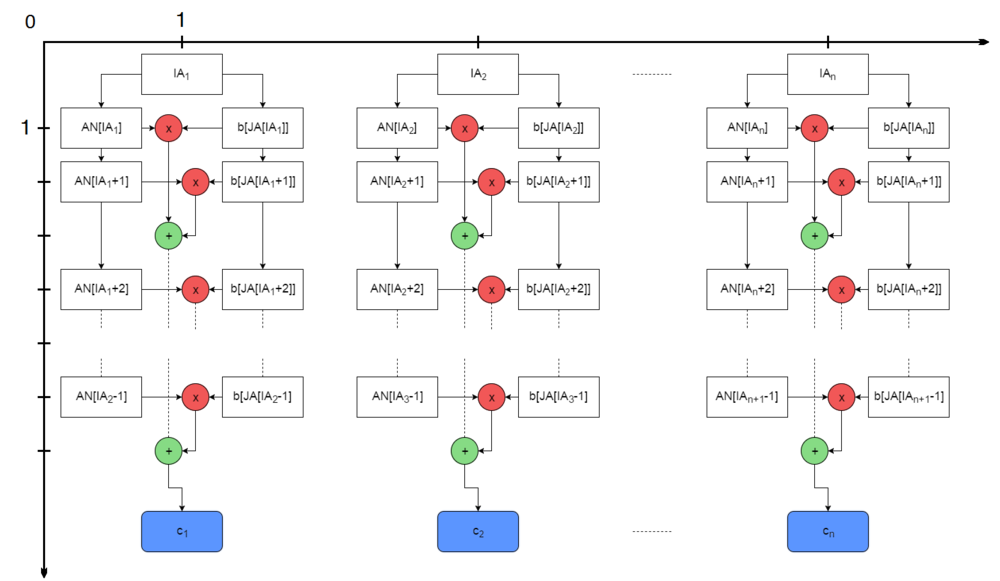
Опишем граф алгоритма как аналитически, так и в виде рисунка.

Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей одной размерности.

Первая группа вершин расположена в двумерной области, соответствующая ей операция вычисляет функцию [math]a \cdot b[/math]. Естественно введённые координаты области таковы:

• [math]i[/math] — меняется в диапазоне от [math]1[/math] до [math]n[/math], принимая все целочисленные значения;
• [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math]k[/math], принимая все целочисленные значения,

где [math]k = k(i) = IA[i+1]-IA[i][/math].

Аргументы операции следующие:

• [math]a[/math] - элемент входных данных, а именно [math]AN[IA_{i}+j-1][/math].
• [math]b[/math] - элемент входных данных, а именно [math]b[IA_{i}+j-1][/math].

Результат срабатывания операции является промежуточным данным алгоритма.

Вторая группа вершин расположена в двумерной области, соответствующая ей операция [math]a + b[/math]. Естественно введённые координаты области таковы:

• [math]i[/math] - меняется в диапазоне от [math]1[/math] до [math]n[/math], принимая все целочисленные значения;
• [math]j[/math] - меняется в диапазоне от [math]1[/math] до [math]k-1[/math], принимая все целочисленные значения,

где [math]k = k(i) = IA[i+1]-IA[i][/math].

Аргументы операции следующие:

• [math]a[/math]:
  • при [math]j = 1[/math] - результат срабатывания операции, соответствующей вершине из первой группы, с координатами [math](i, j)[/math];
  • при [math]j \gt 1[/math] - результат срабатывания операции, соответствующей вершине из второй группы, с координатами [math](i, j - 1)[/math];
• [math]b[/math] — результат срабатывания операции, соответствующей вершине из первой группы, с координатами [math](i, j + 1)[/math].

Результат срабатывания операции:

• при [math]j \lt k - 1[/math] является промежуточным данным алгоритма;
• при [math]j = k - 1[/math] является выходным данным [math]c_{i}[/math].

Описанный граф можно посмотреть на рис.1. Здесь вершины первой группы обозначены красным цветом и отмечены знаком умножения, вершины второй - зелёным цветом и знаком сложения. Вершины, соответствующие входным данным обозначены белым цветом и выходным - синим.

Рисунок 1. Граф алгоритма умножения разреженной матрицы на вектор

1.8 Ресурс параллелизма алгоритма

Для умножения разреженной матрицы общего вида, хранимой в форме RR(C)U, размерности [math]n \times m[/math] на заполненный вектор [math]m \times 1[/math] в параллельном варианте требуется последовательно выполнить следующие ярусы:

• Не более чем [math]m[/math] сложений и умножений ([math]n[/math] вычислений в каждом из ярусов)

При классификации по высоте ЯПФ, таким образом, алгоритм умножения разреженной матрицы на вектор относится к алгоритмам со сложностью [math]O(m)[/math]. При классификации по ширине ЯПФ его сложность будет [math]O(n)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: разреженная матрица общего вида [math]A[/math] размерности [math]n \times m[/math], хранимая в форме RR(C)U посредством массивов [math]IA[/math], [math]JA[/math], [math]AN[/math]. Заполненный вектор-столбец [math]b[/math] с элементами [math]b_{j}[/math] размерности [math]m \times 1[/math].

Объём входных данных: [math]2l+m+n+1[/math], где [math]l[/math] - количество ненулевых элементов в матрице [math]A[/math].

Выходные данные: заполненный вектор-столбец [math]c[/math] с элементами [math]c_{i}[/math] ([math]i = 1,...,n[/math]).

Объём выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейной.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – константа.

Пусть [math]l[/math] - количество ненулевых элементов матрицы [math]A[/math] размерности [math]n \times m[/math]. Пусть [math]x[/math] - объем памяти, используемый для хранения значения элемента матрицы, [math]y[/math] - объём памяти, используемый для хранения номера столбца или строки. В таком случае для хранения матрицы в стандартном представлении нам потребуется объем памяти, равный [math]x \cdot n \cdot m[/math], для хранения в формате RR(C) - [math]y(n + 1) + (x + y)l[/math]. Таким образом хранение в формате RR(C) не является эффективным для матриц, в которых [math]l \gt \frac{xnm - y(n+1)}{x+y}[/math].