Участник:Сергей/Хранение ненулевых элементов разреженной матрицы. Умножение разреженной матрицы на вектор: различия между версиями
Сергей (обсуждение | вклад) |
Сергей (обсуждение | вклад) |
||
| Строка 128: | Строка 128: | ||
Координаты области таковы: | Координаты области таковы: | ||
| − | <math>\cdot</math> <math>i</math> | + | <math>\cdot</math> <math>i</math> — меняется в диапазоне от <math>0</math> до <math>N-1</math>, принимая все натуральные значения; |
| − | <math>\cdot</math> <math>j</math> | + | <math>\cdot</math> <math>j</math> — меняется в диапазоне от <math>1</math> до <math>k-1</math>, принимая все натуральные значения, |
где <math>k = k(i) = row[i+1]-row[i]</math>. | где <math>k = k(i) = row[i+1]-row[i]</math>. | ||
Результат операции: | Результат операции: | ||
| + | |||
<math>\cdot</math> при <math>j < k - 1</math> является '''промежуточным''' данным алгоритма; | <math>\cdot</math> при <math>j < k - 1</math> является '''промежуточным''' данным алгоритма; | ||
| + | |||
<math>\cdot</math> при <math>j = k - 1</math> является '''выходным''' данным <math>out[i]</math>. | <math>\cdot</math> при <math>j = k - 1</math> является '''выходным''' данным <math>out[i]</math>. | ||
Версия 16:33, 15 ноября 2016
Автор: Герасимов Сергей (619)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Разреженная матрица — это матрица с преимущественно нулевыми элементами. В противном случае, если бо́льшая часть элементов матрицы ненулевые, матрица считается плотной.
Нет единства в определении того, какое именно количество ненулевых элементов делает матрицу разрежённой. Разные авторы предлагают различные варианты. Для матрицы порядка n число ненулевых элементов:
~ есть O(n). Такое определение подходит разве что для теоретического анализа асимптотических свойств матричных алгоритмов;
~ в каждой строке не превышает 10 в типичном случае;
~ ограничено [math]n^{1+\gamma}[/math], где [math]\gamma \lt 1[/math].
Огромные разрежённые матрицы часто возникают при решении таких задач, как дифференциальное уравнение в частных производных.
При хранении и преобразовании разрежённых матриц в компьютере бывает полезно, а часто и необходимо, использовать специальные алгоритмы и структуры данных, которые учитывают разрежённую структуру матрицы. Операции и алгоритмы, применяемые для работы с обычными, плотными матрицами, применительно к большим разрежённым матрицам работают относительно медленно и требуют значительных объёмов памяти. Однако разрежённые матрицы могут быть легко сжаты путём записи только своих ненулевых элементов, что снижает требования к компьютерной памяти.
Существуют различные форматы хранения разреженных матриц. Одни предназначены для хранения матриц специального вида (например, ленточных), другие обеспечивают работу с матрицами общего вида. Ниже рассмотрим некоторые весьма распространенные способы представления разреженных матриц.
По-видимому, наиболее очевидным способом хранения произвольной разреженной матрицы является координатный формат: хранятся только ненулевые элементы матрицы, и их координаты (номера строк и столбцов). При данном подходе хранение матрицы A можно обеспечить в трех одномерных массивах:
~ массив ненулевых элементов матрицы A (обозначим его как values);
~ массив номеров строк матрицы A, соответствующих элементам массива values (обозначим его как rows);
~ массив номеров столбцов матрицы A, соответствующих элементам массива values (обозначим его как cols);
Данный способ представления называют полным, поскольку представлена вся матрица А, и неупорядоченным, поскольку элементы матрицы могут храниться в произвольном порядке.
Хотя многие математические библиотеки поддерживают матрично-векторные операции в координатном формате, данный формат обеспечивает медленный доступ к элементам матрицы, и является затратным по используемой памяти. В рассмотренном выше примере избыточность по памяти образом проявляется в массиве rows, в котором строчные координаты хранятся неоптимальным образом.
Перейдем далее к рассмотрению более экономных форматов хранения. Разреженный строчный формат - это одна из наиболее широко используемых схем хранения разреженных матриц. Эта схема предъявляет минимальные требования к памяти и в то же время оказывается очень удобной для нескольких важных операций над разреженными матрицами: сложения, умножения, перестановок строк и столбцов, транспонирования, решения линейных систем с разреженными матрицами коэффициентов как прямыми, так и итерационными методами и т. д.
В соответствии с рассматриваемой схемой для хранения матрицы A требуется три одномерных массива:
~ массив ненулевых элементов матрицы A, в котором они перечислены по строкам от первой до последней (обозначим его опять как values);
~ массив номеров столбцов для соответствующих элементов массива values (обозначим его как cols);
~ массив указателей позиций, с которых начинается описание очередной строки (обозначим его pointer). Описание k-й строки хранится в позициях с pointer[k]-й по (pointer[k+1]–1)-ю массивов values и cols. Если pointer[k]=pointer[k+1], то k-я строка пустая. Если матрица A состоит из n строк, то длина массива pointer будет n+1.
Данный способ представления также является полным, и упорядоченным, поскольку элементы каждой строки хранятся в соответствии с возрастанием столбцовых индексов.
Очевидно, что объем памяти, требуемый для хранения вектора pointer, значительно меньше, чем для хранения вектора rows. Более того, разреженный строчный формат обеспечивает эффективный доступ к строчкам матрицы; доступ к столбцам по прежнему затруднен. Поэтому предпочтительно использовать этот способ хранения в тех алгоритмах, в которых преобладают строчные операции.
Существует также разреженный столбцовый формат, который строится аналогичным способом.
Теперь, разобравшись со способами хранения разреженных матриц, можно перейти к алгоритму умножения разреженной матрицы на вектор. Умножение матрицы на вектор является подзадачей для нахождения решений СЛАУ итерационными методами.
1.2 Математическое описание алгоритма
Пусть матрица размером [math]N\times M[/math] содержит в себе [math]NZ[/math] ненулевых элементов, где [math]NZ\ll N^2[/math]
Условимся использовать строчный формат хранения матрицы, который описан выше.
На входе у нас 4 массива: val(ненулевые элементы матрицы), col(номера столбцов), row(массив указателей) и vec(вектор, на который мы умножаем матрицу).
На выходе получим вектор out.
[math]out_i = \sum_{j=row_i}^{row_{i+1} - 1} val_j \cdot vec_{col_j}, \ i=\overline{0,N-1}[/math], где [math]N[/math] - число строк матрицы.
1.3 Вычислительное ядро алгоритма
Ядром алгоритма является вычисление сумм произведений:
[math]out_i = \sum_{j=row_i}^{row_{i+1} - 1} val_j \cdot vec_{col_j}[/math]
Итого: [math]NZ[/math] умножений + [math]x[/math] сложений([math]NZ-N\lt x\lt NZ-1[/math]).
1.4 Макроструктура алгоритма
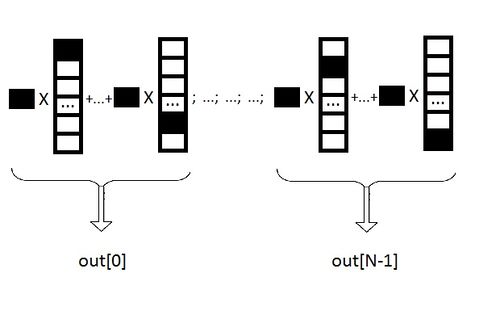
Метод состоит из вычисления неполных скалярных произведений.
Элементы из массива val умножаются на элементы из массива vec с соответствующим индексом. Черным отмечены ненулевые элементы.
1.5 Схема реализации последовательного алгоритма
Предполагается, что матрица представлена в разреженном строчном формате.
for(i=0; i<N; i++)
{
out[i]=0;
for(j=row[i]; j<row[i+1]; j++)
{
out[i] += val[j]*vec[col[j]];
}
}
Внешний цикл - цикл по элементам выходного вектора. Внутренний - цикл по строкам разреженной матрицы. Во внутреннем цикле реализовано накопление сумм произведений в выходной элемент. Индекс j показывает с какого по какой элемент нужно считать из val (вектор с ненулевыми значениями матрицы), а также позволяет определить в каких столбцах расположены эти значения в матрице (с помощью вектора col). Минимальное и максимальное значение j узнается из вектора row.
1.6 Последовательная сложность алгоритма
[math]\bullet \ NZ[/math] умножений
[math]\bullet \ x[/math] сложений([math]NZ-N\lt x\lt NZ-1[/math]).
Всего [math]2NZ[/math] операций, где [math]NZ[/math] - количество ненулевых элементов.
1.7 Информационный граф
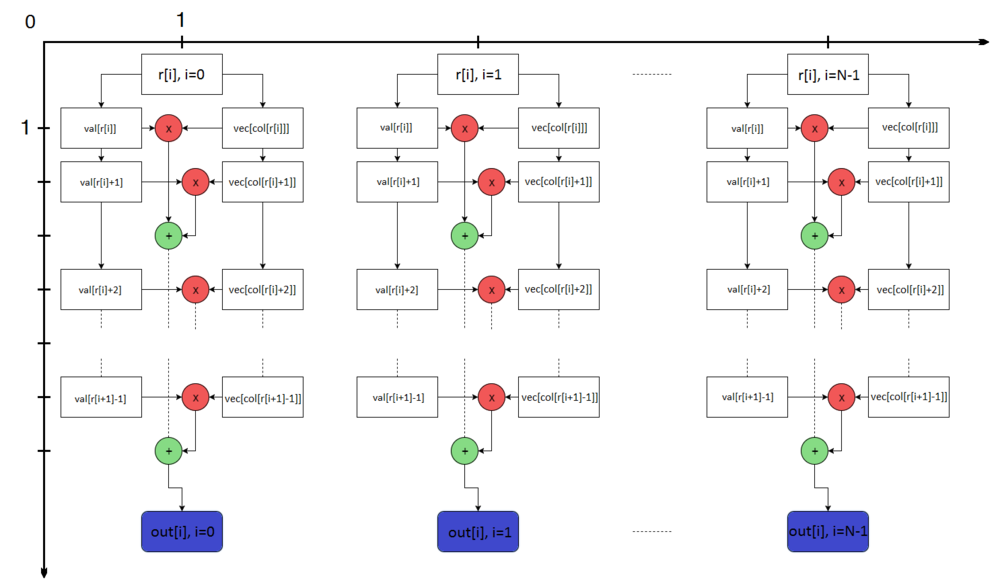
Опишем граф алгоритма.
Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей одной размерности.
Первая группа вершин расположена в двумерной области, соответствующая ей операция вычисляет функцию [math]a \cdot b[/math]. Координаты области следующие:
[math]\cdot[/math] [math]i[/math] — меняется в диапазоне от [math]0[/math] до [math]N-1[/math], принимая все натуральные значения;
[math]\cdot[/math] [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math] k [/math], принимая все натуральные значения,
где [math]k = k(i) = row[i+1]-row[i][/math]. (На рисунке вместо обозначения row использовано обозначение r).
Результаты операции - промежуточные данные алгоритма.
Вторая группа вершин расположена в двумерной области, соответствующая ей операция вычисляет функцию [math]a + b[/math]. Координаты области таковы:
[math]\cdot[/math] [math]i[/math] — меняется в диапазоне от [math]0[/math] до [math]N-1[/math], принимая все натуральные значения;
[math]\cdot[/math] [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math]k-1[/math], принимая все натуральные значения,
где [math]k = k(i) = row[i+1]-row[i][/math].
Результат операции:
[math]\cdot[/math] при [math]j \lt k - 1[/math] является промежуточным данным алгоритма;
[math]\cdot[/math] при [math]j = k - 1[/math] является выходным данным [math]out[i][/math].
Описанный граф изображен на Рис.2. Здесь вершины первой группы обозначены красным цветом и отмечены знаком умножения, вершины второй - зелёным цветом и знаком сложения. Вершины, соответствующие входным данным обозначены белым цветом и выходным - синим.
1.8 Ресурс параллелизма алгоритма
При наличии бесконечного числа процессоров для умножения разреженной матрицы на вектор потребуется:
~ 1 ярус умножений
~ [math]Z-1[/math] операция сложения, где Z - максимальное число ненулевых элементов в строке.
Максимальное число требуемых процессоров - NZ.
1.9 Входные и выходные данные алгоритма
Входные данные:
~ массив ненулевых элементов матрицы A, в котором они перечислены по строкам от первой до последней (обозначим его как val);
~ массив номеров столбцов для соответствующих элементов массива val (обозначим его как col);
~ массив указателей позиций, с которых начинается описание очередной строки (обозначим его row);
~ вектор, на который будет умножаться матрица (обозначим его vec).
Объем входных данных:
Для матрицы размером [math]N\times M[/math], содержащей в себе [math]NZ[/math] ненулевых элементов, где [math]NZ\ll N^2[/math],
~ вектор val - NZ элементов;
~ вектор col - NZ элементов;
~ вектор row - N+1 элемент;
~ вектор vec - M элементов.
Выходные данные:
Вектор out размером N.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным.
Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – чуть меньше единицы.
Данный алгоритм обладает свойством детерминированности.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Эффективная работа с разреженными матрицами реализована во многих библиотеках, например, Intel Math Kernel Library, базирующуюся на библиотеках BLAS и LAPACK, также математических пакет Matlab имеет собственную реализацию.
3 Литература
[1] Писсанецки С. Технология разреженных матриц. - М.: Мир, 1988. — 410 с.
[2] https://software.intel.com/sites/default/files/m/d/4/1/d/8/LW_SparseMM_ppt.pdf