Участник:Сергей/Хранение ненулевых элементов разреженной матрицы. Умножение разреженной матрицы на вектор

Автор: Герасимов Сергей (619)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Разреженная матрица — это матрица с преимущественно нулевыми элементами. В противном случае, если бо́льшая часть элементов матрицы ненулевые, матрица считается плотной.

Нет единства в определении того, какое именно количество ненулевых элементов делает матрицу разрежённой. Разные авторы предлагают различные варианты. Для матрицы порядка n число ненулевых элементов:

~ есть O(n). Такое определение подходит разве что для теоретического анализа асимптотических свойств матричных алгоритмов;

~ в каждой строке не превышает 10 в типичном случае;

~ ограничено [math]n^{1+\gamma}[/math], где [math]\gamma \lt 1[/math].

Огромные разрежённые матрицы часто возникают при решении таких задач, как дифференциальное уравнение в частных производных.

При хранении и преобразовании разрежённых матриц в компьютере бывает полезно, а часто и необходимо, использовать специальные алгоритмы и структуры данных, которые учитывают разрежённую структуру матрицы. Операции и алгоритмы, применяемые для работы с обычными, плотными матрицами, применительно к большим разрежённым матрицам работают относительно медленно и требуют значительных объёмов памяти. Однако разрежённые матрицы могут быть легко сжаты путём записи только своих ненулевых элементов, что снижает требования к компьютерной памяти.

Существуют различные форматы хранения разреженных матриц. Одни предназначены для хранения матриц специального вида (например, ленточных), другие обеспечивают работу с матрицами общего вида. Ниже рассмотрим некоторые весьма распространенные способы представления разреженных матриц.

По-видимому, наиболее очевидным способом хранения произвольной разреженной матрицы является координатный формат: хранятся только ненулевые элементы матрицы, и их координаты (номера строк и столбцов). При данном подходе хранение матрицы A можно обеспечить в трех одномерных массивах:

~ массив ненулевых элементов матрицы A (обозначим его как values);

~ массив номеров строк матрицы A, соответствующих элементам массива values (обозначим его как rows);

~ массив номеров столбцов матрицы A, соответствующих элементам массива values (обозначим его как cols);

Данный способ представления называют полным, поскольку представлена вся матрица А, и неупорядоченным, поскольку элементы матрицы могут храниться в произвольном порядке.

Хотя многие математические библиотеки поддерживают матрично-векторные операции в координатном формате, данный формат обеспечивает медленный доступ к элементам матрицы, и является затратным по используемой памяти. В рассмотренном выше примере избыточность по памяти образом проявляется в массиве rows, в котором строчные координаты хранятся неоптимальным образом.

Перейдем далее к рассмотрению более экономных форматов хранения. Разреженный строчный формат - это одна из наиболее широко используемых схем хранения разреженных матриц. Эта схема предъявляет минимальные требования к памяти и в то же время оказывается очень удобной для нескольких важных операций над разреженными матрицами: сложения, умножения, перестановок строк и столбцов, транспонирования, решения линейных систем с разреженными матрицами коэффициентов как прямыми, так и итерационными методами и т. д.

В соответствии с рассматриваемой схемой для хранения матрицы A требуется три одномерных массива:

~ массив ненулевых элементов матрицы A, в котором они перечислены по строкам от первой до последней (обозначим его опять как values);

~ массив номеров столбцов для соответствующих элементов массива values (обозначим его как cols);

~ массив указателей позиций, с которых начинается описание очередной строки (обозначим его pointer). Описание k-й строки хранится в позициях с pointer[k]-й по (pointer[k+1]–1)-ю массивов values и cols. Если pointer[k]=pointer[k+1], то k-я строка пустая. Если матрица A состоит из n строк, то длина массива pointer будет n+1.

Данный способ представления также является полным, и упорядоченным, поскольку элементы каждой строки хранятся в соответствии с возрастанием столбцовых индексов.

Очевидно, что объем памяти, требуемый для хранения вектора pointer, значительно меньше, чем для хранения вектора rows. Более того, разреженный строчный формат обеспечивает эффективный доступ к строчкам матрицы; доступ к столбцам по прежнему затруднен. Поэтому предпочтительно использовать этот способ хранения в тех алгоритмах, в которых преобладают строчные операции.

Существует также разреженный столбцовый формат, который строится аналогичным способом.

Теперь, разобравшись со способами хранения разреженных матриц, можно перейти к алгоритму умножения разреженной матрицы на вектор. Умножение матрицы на вектор является подзадачей для нахождения решений СЛАУ итерационными методами.

1.2 Математическое описание алгоритма

Пусть матрица размером [math]N\times M[/math] содержит в себе [math]NZ[/math] ненулевых элементов, где [math]NZ\ll N^2[/math]

Условимся использовать строчный формат хранения матрицы, который описан выше.

На входе у нас 4 массива: val(ненулевые элементы матрицы), col(номера столбцов), row(массив указателей) и vec(вектор, на который мы умножаем матрицу).

На выходе получим вектор out.

[math]out_i = \sum_{j=row_i}^{row_{i+1} - 1} val_j \cdot vec_{col_j}, \ i=\overline{0,N-1}[/math], где [math]N[/math] - число строк матрицы.

1.3 Вычислительное ядро алгоритма

Ядром алгоритма является вычисление сумм произведений:

[math]out_i = \sum_{j=row_i}^{row_{i+1} - 1} val_j \cdot vec_{col_j}[/math]

Итого: [math]NZ[/math] умножений + [math]x[/math] сложений([math]NZ-N\lt x\lt NZ-1[/math]).

1.4 Макроструктура алгоритма

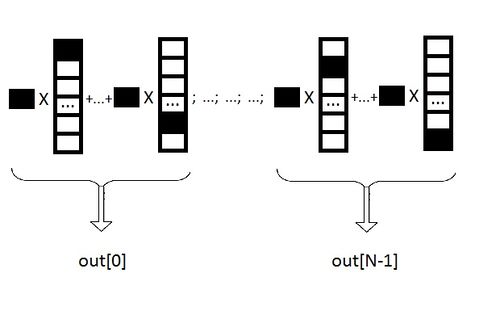
Метод состоит из вычисления неполных скалярных произведений.

Рис.1 Умножение разреженной матрицы на вектор

Элементы из массива val умножаются на элементы из массива vec с соответствующим индексом. Черным отмечены ненулевые элементы.

1.5 Схема реализации последовательного алгоритма

Предполагается, что матрица представлена в разреженном строчном формате.

   for(i=0; i<N; i++)
   {
       out[i]=0;
       for(j=row[i]; j<row[i+1]; j++)
       {
           out[i] += val[j]*vec[col[j]];
       }
   }

Внешний цикл - цикл по элементам выходного вектора. Внутренний - цикл по строкам разреженной матрицы. Во внутреннем цикле реализовано накопление сумм произведений в выходной элемент. Индекс j показывает с какого по какой элемент нужно считать из val (вектор с ненулевыми значениями матрицы), а также позволяет определить в каких столбцах расположены эти значения в матрице (с помощью вектора col). Минимальное и максимальное значение j узнается из вектора row.

1.6 Последовательная сложность алгоритма

[math]\bullet \ NZ[/math] умножений

[math]\bullet \ x[/math] сложений([math]NZ-N\lt x\lt NZ-1[/math]).

Всего [math]2NZ[/math] операций, где [math]NZ[/math] - количество ненулевых элементов.

1.7 Информационный граф

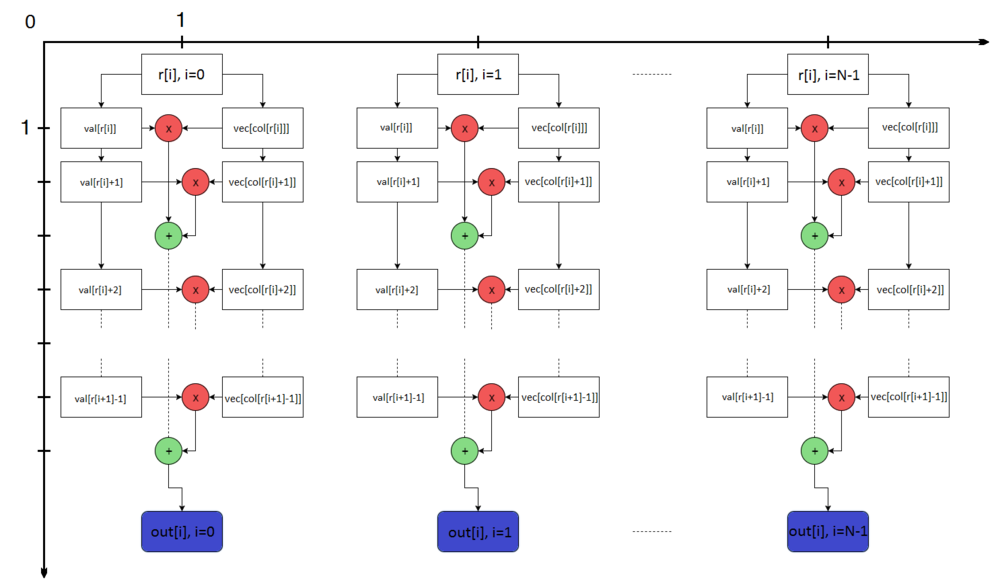
Опишем граф алгоритма.

Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей одной размерности.

Первая группа вершин расположена в двумерной области, соответствующая ей операция вычисляет функцию [math]a \cdot b[/math]. Координаты области следующие:

[math]\cdot[/math] [math]i[/math] — меняется в диапазоне от [math]0[/math] до [math]N-1[/math], принимая все натуральные значения;

[math]\cdot[/math] [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math] k [/math], принимая все натуральные значения,

где [math]k = k(i) = row[i+1]-row[i][/math]. (На рисунке вместо обозначения row использовано обозначение r).

Результаты операции - промежуточные данные алгоритма.

Вторая группа вершин расположена в двумерной области, соответствующая ей операция вычисляет функцию [math]a + b[/math]. Координаты области таковы:

[math]\cdot[/math] [math]i[/math] — меняется в диапазоне от [math]0[/math] до [math]N-1[/math], принимая все натуральные значения;

[math]\cdot[/math] [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math]k-1[/math], принимая все натуральные значения,

где [math]k = k(i) = row[i+1]-row[i][/math].

Результат операции:

[math]\cdot[/math] при [math]j \lt k - 1[/math] является промежуточным данным алгоритма;

[math]\cdot[/math] при [math]j = k - 1[/math] является выходным данным [math]out[i][/math].

Описанный граф изображен на Рис.2. Здесь вершины первой группы обозначены красным цветом и отмечены знаком умножения, вершины второй - зелёным цветом и знаком сложения. Вершины, соответствующие входным данным обозначены белым цветом и выходным - синим.

Рис.2 Умножение разреженной матрицы на вектор. Информационный граф

1.8 Ресурс параллелизма алгоритма

При наличии бесконечного числа процессоров для умножения разреженной матрицы на вектор потребуется:

~ 1 ярус умножений

~ [math]Z-1[/math] операция сложения, где Z - максимальное число ненулевых элементов в строке.

Максимальное число требуемых процессоров - NZ.

1.9 Входные и выходные данные алгоритма

Входные данные:

~ массив ненулевых элементов матрицы A, в котором они перечислены по строкам от первой до последней (обозначим его как val);

~ массив номеров столбцов для соответствующих элементов массива val (обозначим его как col);

~ массив указателей позиций, с которых начинается описание очередной строки (обозначим его row);

~ вектор, на который будет умножаться матрица (обозначим его vec).

Объем входных данных:

Для матрицы размером [math]N\times M[/math], содержащей в себе [math]NZ[/math] ненулевых элементов, где [math]NZ\ll N^2[/math],

~ вектор val - NZ элементов;

~ вектор col - NZ элементов;

~ вектор row - N+1 элемент;

~ вектор vec - M элементов.

Выходные данные:

Вектор out размером N.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным.

Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – чуть меньше единицы.

Данный алгоритм обладает свойством детерминированности.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

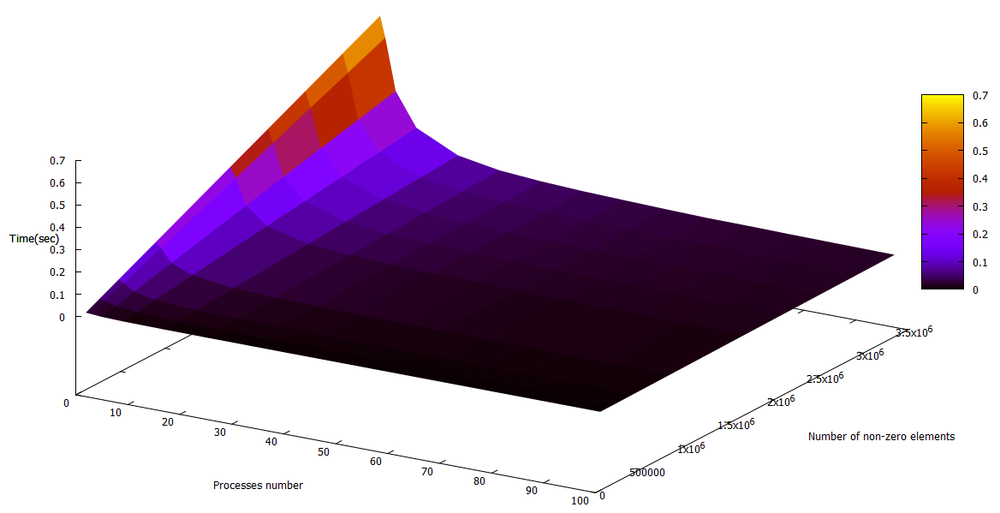
Проведём исследование масштабируемости параллельной реализации умножения разреженной матрицы на вектор. Исследование проводилось на вычислительном комплексе Blue Gene/P. Вычисления проводились с помощью следующего программного кода. Матрицы генерировались случайным образом.

На следующем рисунке показана зависимость времени выполнения алгоритма от числа используемых процессоров и количества ненулевых элементов матрицы. Можно заметить, что скорость вычисления при переходе с последовательной на параллельную версию возросла значительно. Однако, дальнейшее увеличение числа вычислительных устройств не дает сильного прироста производительности. Это объясняется быстрым ростом накладных расходов на организацию параллельного выполнения.

Рис.3 Умножение разреженной матрицы на вектор. Масштабируемость

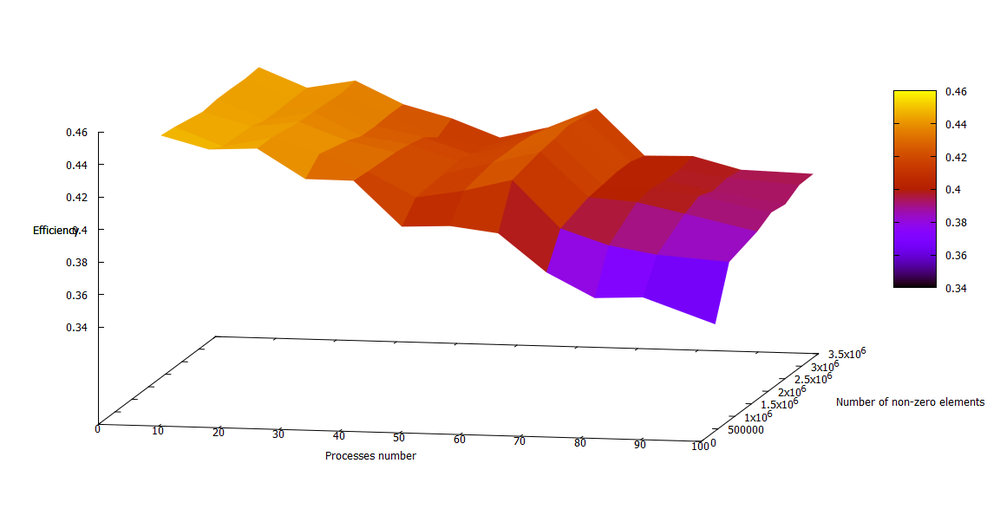
На рисунке ниже изображен график эффективности в зависимости от числа процессоров и размера задачи. Можно заметить небольшой всплеск эффективности при использовании 64 процессоров.

Рис.4 Умножение разреженной матрицы на вектор. Эффективность

2.7 Существующие реализации алгоритма

Эффективная работа с разреженными матрицами реализована во многих библиотеках, например, Intel Math Kernel Library, базирующуюся на библиотеках BLAS и LAPACK, также математических пакет Matlab имеет собственную реализацию.

3 Литература

[1] Писсанецки С. Технология разреженных матриц. - М.: Мир, 1988. — 410 с.

[2] https://software.intel.com/sites/default/files/m/d/4/1/d/8/LW_SparseMM_ppt.pdf