Участница:Эльвира Ахиярова/Итерационный метод решения системы линейных алгебраических уравнений GMRES (обобщенный метод минимальных невязок)

Обобщеннный метод минимальных невязок
Последовательный алгоритм
Последовательная сложность	[math]O(mn+m^2+n^2)[/math]
Объём входных данных	[math]n^2+n+1[/math]
Объём выходных данных	[math]n[/math]

Основные авторы описания: Э.А.Ахиярова

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Обобщенный метод минимальных невязок (GMRES) - это итерационный метод для нахождения приближенного решения системы линейных алгебраических уравнений [math]Ax = b [/math] с произвольной матрицей [math]A[/math]. Алгоритм был преложен в 1986 году Йозефом Саадом и Мартином Г. Шульцем .

В то время как применение классических итерационных алгоритмов для решения СЛАУ ограничивается либо диагональным преобладанием, либо положительной определенностью матрицы, GMRES может быть использован для систем с произвольной невырожденной матрицей [math]A[/math]. Данный метод опирается на итерации Арнольди для нахождения минимизирующего невязку вектора из подпространства Крылова .

Основным недостатком метода GMRES является поитерационное увеличение объема требуемой памяти. В связи с этим, для некоторых вычислительных систем выполенние программы метода может быть невозможным. Для некоторых систем используют модифицированный обобщенный метод минимальных невязок - GMRES(m), который подразумевает использование рестартов, существенно сокращающих объемы необходимой памяти.

Ключевая идея обобщенного метода минимальных невязок основана на решении задачи наименьших квадратов на каждом итерационном шаге. На каждом [math]k[/math]-м шаге точное решение [math]x^* = A^{-1}b [/math] аппроксимируется вектором [math]x_k \in K_k[/math], таким образом, что:

[math] \|r_k{\|}_2 = \|Ax_k-b{\|}_2 \to \min [/math],

где [math]K_k[/math] - подпространство Крылова [math] k [/math] - го порядка.

1.2 Математическое описание алгоритма

Исходные данные: Матрица [math]A \in R^{n\times n}[/math], вектор правой части [math]b \in R^n[/math].

Вычисляемые данные: Приближенное решение [math]\tilde{x} \in R^n[/math] системы [math]Ax = b[/math].

На каждом [math]k[/math]-м шаге метода решение [math]x_k[/math] рассматривается в виде [math]x_0+Vy_k[/math], где столбцы [math]v_k[/math] матрицы [math]V[/math] находятся с помощью процесса Арнольди для построения ортонормированного базиса [math]\{v_1, v_2, \dots, v_k\}[/math] подпространства Крылова [math]K_k(A, v_1)[/math], вектор [math]y_k[/math] представляет собой решение системы [math]H_ky_k = \beta_k e_1[/math], где [math]H_k[/math] - верхняя матрица Хессенберга размера [math]k\times k[/math], элементы которой формируются в процессе ортогонализации Арнольди, [math]\beta_k = \|r_0{\|}_2, \ r_0 = b - Ax_0 [/math], и, наконец, [math]e_1[/math] - канонический вектор [math]{\begin{pmatrix}1&0&\dots 0\end{pmatrix}}^T[/math] размерности [math]k[/math]

Рассмотрим подробнее процесс ортогонализации Арнольди:

1.2.1 Процесс Арнольди

Исходные данные: начальный ортонормированный вектор [math]v_1[/math] и размерность [math]k[/math]

Вычисляемые данные: Ортонормированный базис [math]\{v_1, v_2, \dots, v_k\}[/math] подпространства [math]K_k(A, v_1)[/math]

Формулы метода:

[math] \begin{align} &\omega = Av_j \\ &h_{ij} = (\omega, v_i) \\ &\omega = \omega - h_{ij}v_i \\ &h_{(i+1)j} = \|\omega\| \\ &v_{j+1} = \frac{\omega}{h_{(i+1)j}} \\ &j = \overline{1,k}, \ i = \overline{1,j} \end{align} [/math]

В результате выполнения процесса Арнольди получаем:

[math]V_k =\{v_1, v_2, \dots, v_k\}[/math] - ортонормированный базис подпространства Крылова

[math]\overline{V_k} = \{v_1, v_2, \dots, v_k, v_{k+1}\}[/math] - матрица, расширенная последним вычисленным вектором [math]v_{k+1}[/math]

[math]H_k[/math] - верхняя Хессенбергова матрица, элементы которой равны коэффициентам ортогонализации:

[math]H_k = \begin{pmatrix} h_{11} & h_{12} & h_{13} & h_{14} & \dots & h_{1k} \\ h_{21} & h_{22} & h_{23} & h_{24} & \dots & h_{2k} \\ 0 & h_{32} & h_{33} & h_{34} & \dots & h_{3k} \\ \vdots & &\ddots & \ddots & & \vdots \\ 0 & \dots & 0 & h_{k-1,k-2}& h_{k-1, k-1} & h_{k-1, k} \\ 0 & \dots & 0 & 0 & h_{k, k-1} & h_{k, k} \\ 0 & \dots & & & 0& h_{k+1, k} \end{pmatrix} [/math]

1.2.2 Минимизация нормы невязки

Выполнив несложные преобразования можно получить выражение для невязки на [math]k[/math]- й итерации:

[math] r_k = \beta e_1 - H_ky_k [/math]

Очевидно, что для задачи

[math] \|r_k{\|}_2 \to \min [/math]

минимум достигается при

[math] H_ky_k = \beta e_1 [/math]

Для решения последней системы матрица [math]H_k[/math] приводится к верхнему треугольному виду с помощью [math] k [/math] вращений Гивенса:

[math] R_k = \Omega_k\Omega_{k-1}\dots \Omega_1 [/math],

[math] \Omega_i = \begin{pmatrix} 1 & &&&&&& \\ &\ddots &&&&&&\\ &&1&&&&& \\ &&&c_i&s_i &&& \\ &&&-s_i& c_i &&&\\ &&&&&1&&& \\ &&&&&&\ddots&\\ &&&&&&&1 \\ \end{pmatrix}, \quad s_i = \frac{h_{i+1,i}}{\sqrt{h_{ii}^2+h_{i+1,i}^2}}, \quad c_i = \frac{h_{ii}}{\sqrt{h_{ii}^2+h_{i+1,i}^2}}[/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро последовательной версии метода GMRES состоит из вычислений произведений матрицы на вектор и скалярного произведения в процессе Арнольди и произведений матрицы на вектор, обращений верхней треугольной матрицы для нахождения решения задачи минимизации невязки.

1.4 Макроструктура алгоритма

В методе используются следующие макрооперции:

• Умножение матрицы на вектор
• Вычисление скалярного произведение двух векторов
• Нахождени [math]l_2[/math]-нормы вектора
• Умножение матриц специальной структуры
• Решение системы уравнений с верхней треугольной матрицей

1.5 Схема реализации последовательного алгоритма

Для обобщенного метода мимнимальных невязок число векторов порядка [math]n[/math], которых необходимо хранить в памяти, растет линейно с ростом [math]k[/math], в то время как число умножений имеет квадратичную зависимость от числа итераций. Этот факт является мотивацией для того, чтобы использовать метод минимальных невязок с рестартами. Вместо того, чтобы формировать базис размерности [math]k[/math], выбирается параметр [math]m \lt \lt n [/math] и с помощью ортонормированного базиса размерности [math]m[/math] строится приближенное решение. Посредством такой схемы необходимое количество памяти может быть оценено заранее и оставаться внутри определенных пределов. Приведем подробное описание алгоритма GMRES c рестартами:

1. [math]k = 0 [/math]; инициализировать [math]x_0[/math]; [math]r_0=b-Ax_0[/math] и [math]v_1=\frac{r_0}{\|r_0 \|}[/math]

2. Выполнить [math]m[/math] шагов процессса Арнольди:

  Для [math] j  = \overline{1,m} [/math] выполнять:
     [math]
      \omega = Av_j 
      [/math]
     Для [math] i = \overline{1,j} [/math] выполнять: 
          [math]
           \begin{align}
            &h_{ij} = (\omega, v_i)   \\
            &\omega = \omega - h_{ij}v_i \\
            \end{align}
           [/math]
      [math]
          \begin{align}
           h_{(i+1)j} = \|\omega\| \\
           v_{j+1} = \frac{\omega}{h_{(i+1)j}} \\
         \end{align}
      [/math]   

3. Вычислить [math]y_m=\arg\min_{y} \| \beta e_1 - H_m y \|,\ y \in \R^m[/math] и [math]x_m=x_0+V_my_m[/math]

4. Вычислить [math]r_m=b-Ax_m[/math]. Если требуемая точность достигнута, остановиться

5. Рестарт:

  [math]x_0 = x_m[/math]
  [math]r_m = \frac{r_m}{\|r_m\|}[/math]
  Перейти к шагу 2.

1.6 Последовательная сложность алгоритма

Вычислительная сложность метода GMRES складывается из сложности решения задачи минимизации невязки и сложности процесса Арнольди. Так как в задаче минимизации невязки матрица системы имеет размер [math]m+1 \times m[/math], для нахождения решения требуется [math]O(m^2)[/math] операций. Процесс Арнольди предполагает выполнение [math]O(mn)[/math] операций плюс [math]O(n^2)[/math] операций для умножений матрицы на вектор.

1.7 Информационный граф

Основным ресурсом параллелизма будут являться умножение матрицы на вектор и вычисление скалярных произведений. Представим информационные графы для данных алгоритмов:

• 

  Рисунок 1. Граф последовательного умножения плотной матрицы на вектор с отображением входных и выходных данных

• 

  Рисунок 2. Последовательно-параллельное вычисление скалярного произведения

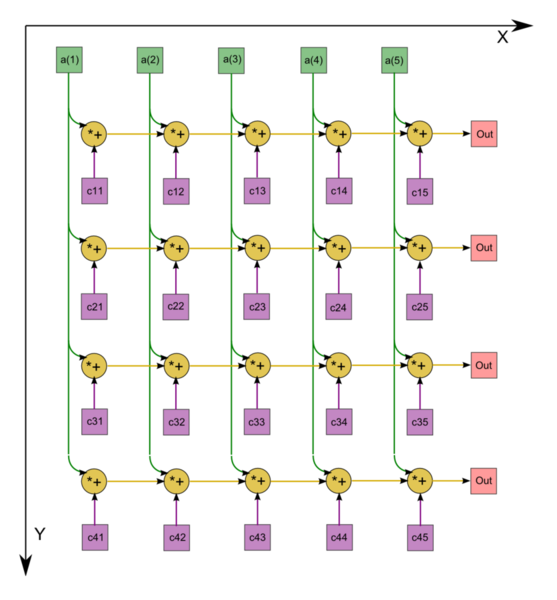
Граф алгоритма умножения плотной матрицы на вектор состоит из одной группы вершин, расположенной в целочисленных узлах двумерной области, соответствующая ей операция [math]a+bc[/math].

Описанный граф выполнен для случая [math]m = 4, n = 5[/math]. Изображена подача только входных данных из вектора [math]x[/math], подача элементов матрицы [math]A[/math], идущая во все вершины, на рисунке не представлена.

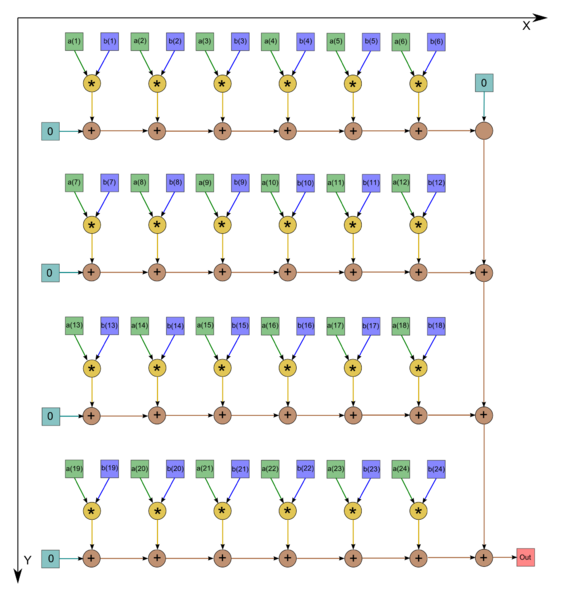
Граф алгоритма нахождения скалярного произведения двух векторов состоит из двух групп вершин, им соответсвуют операции [math]a*b, \quad c+d[/math]. Данный граф изображен для случая [math]n = 24[/math].

1.8 Ресурс параллелизма алгоритма

Для умножения квадратной матрицы на вектор порядка [math]n[/math] в параллельном варианте требуется последовательно выполнить следующие ярусы:

• по [math]n[/math] ярусов умножений и сложений (в каждом из ярусов — [math]n[/math] операций).

Для умножения матрицы размером [math]n[/math] строк на [math]n[/math] столбцов на вектор порядка [math]n[/math] в последовательном (наиболее быстром) варианте требуется:

• по [math]n[/math] ярусов умножений и сложений (в каждом из ярусов — [math]n[/math] операций).

При этом использование режима накопления требует совершения умножений и сложений в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.

При классификации по высоте ЯПФ, таким образом, алгоритм умножения матрицы на вектор относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет линейной.

Для вычисления скалярного произведения векторов размерности [math]n[/math] параллельном варианте требуется последовательно выполнить следующие ярусы:

• 1 ярус вычисления произведений,
• [math]k - 1[/math] ярусов суммирования по частям массивов ([math]p[/math] ветвей),
• [math]p - 1[/math] ярусов суммирования (одна последовательная ветвь),

где [math]p[/math] - количество процессоров, [math]k[/math]- номер процессора.

Таким образом, в параллельном варианте критический путь алгоритма (и соответствующая ему высота ЯПФ) будет зависеть от произведённого разбиения массива на части. В оптимальном случае ([math]p = \sqrt{n}[/math]) высота ЯПФ будет равна [math] 2 \sqrt{n} - 1[/math]. При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам со сложностью «корень квадратный». При классификации по ширине ЯПФ его сложность также будет «корень квадратный».

1.9 Входные и выходные данные алгоритма

Входные данные: Матрица [math]A \in R^{n\times n}[/math], вектор [math]b \in R^n[/math], точность [math]\varepsilon[/math]. Объём: [math]n^2 + n + 1[/math]

Выходные данные: Вектор [math]x_m \in R^n[/math]. Объём: [math]n[/math]

1.10 Свойства алгоритма

В точной арифметике GMRES всегда сходится не более чем за [math]n [/math] итераций (т.к. [math]K_n = R^n = Im(A)[/math]). При этом последовательность решений сходится монотонно, в связи с тем, что [math]\|r_{m+1}\| \le \|r_m\|[/math]. Этот факт справедлив из-за того, что подпространства, по которым минимизируется [math]\|r_m\|[/math], вложены друг в друга: [math]K_m \subset K_{m+1}[/math]. Таким образом, минимизация по подпрастранствам большей размерности приведет нас к меньшей норме невязки.

Скорость сходимости метода зависит от расположения собственных значений матрицы [math]A[/math] на комплексной плоскости. Для быстрой сходимости, собственные значения должны быть сконцентрированны на достаточном расстоянии от начала координат. Заметим, что расположение собственных чисел намного важнее, чем число обусловленности матрицы [math]A[/math], являющимся главным критерием быстрой сходимости для метода сопряженных градиентов.

Если обобщенный метод минимальных невязок применяется к СЛАУ с матрицами, обладающими "хорошим" распределением собственных чисел, то он может работать быстрее чем стандартное [math]LU[/math] разложение даже в том случае, если матрица плотна и неструктурированна.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Реализации обобщенного метода минимальных невязок (GMRES) присутствуют во многих пакетах. Приведем некоторые из них:

• LINPACK
• JAMA/C++
• ATLAS
• Intel MLK
• IML++
• LAPACK
• MTL
• SPARSKIT
• WSMP
• PETSC
• SciPy
• Matlab
• FEniCS Project

3 Литература

[1] A parallel implementation of the restarted GMRES iterative algorithm for nonsymmetric systems of linear equations, Rudnei Dias da Cunha, Centro de Processamento de Dados, Universidade Federal do Rio Grande do Sul, Brazil and Computing Laboratory, University of Kent, Canterbury, UK and Tim Hopkins, Computing Laboratory, University of Kent, Canterbury, UK, 1993

[2] Gene H. Golub, Charles F. Van Loan, Matrix and Computations, 4th edition