Участник:Бобцов Борис/Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки: различия между версиями
Stalles (обсуждение | вклад) |
Stalles (обсуждение | вклад) |
||
| Строка 235: | Строка 235: | ||
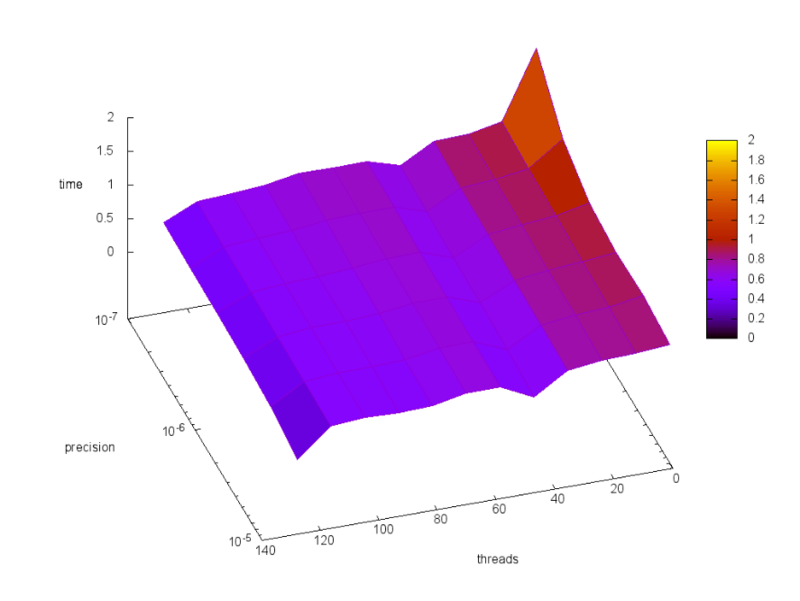
[[Файл:Png_mapoftime.png|thumb|center|800px|Рис.3. Время работы алгоритма в зависимости от числа процессов и точности вычислений ]] | [[Файл:Png_mapoftime.png|thumb|center|800px|Рис.3. Время работы алгоритма в зависимости от числа процессов и точности вычислений ]] | ||
| + | |||
| + | |||
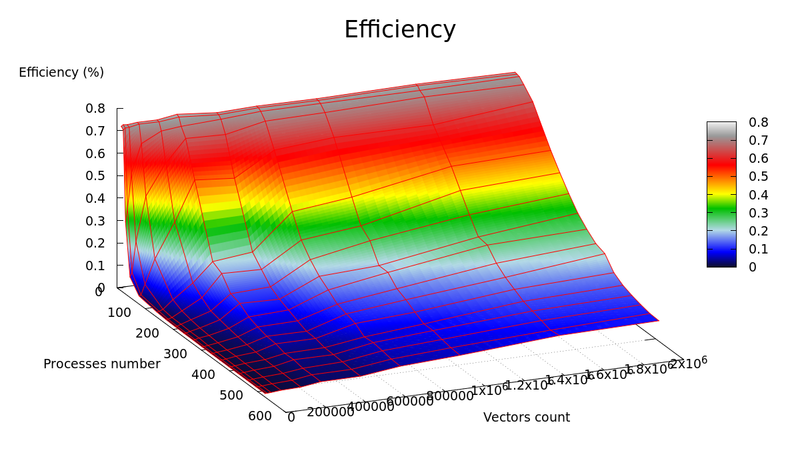
| + | [[Файл:efficiency.png|thumb|center|800px|Рис.4. Эффективность алгоритма в зависимости от числа процессоров и точности вычислений ]] | ||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
Версия 20:58, 27 ноября 2016
| Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки | |
| Последовательный алгоритм | |
| Последовательная сложность | [math] O\left( n \right) [/math], где [math] n [/math] - количество подотрезков, на которые разбился исходный отрезок |
| Объём входных данных | [math]1[/math] функция [math]1[/math] переменной, [math]3[/math] числа (границы отрезка интегрирования, точность) |
| Объём выходных данных | [math]1[/math] число |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math] log(n) [/math] |
| Ширина ярусно-параллельной формы | [math] n [/math] |
Автор статьи: Бобцов Борис (группа 619)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Пусть требуется вычислить определённый интеграл [math]I = \int_a^b{f(x)dx}[/math] от непрерывной функции [math]f(x)[/math]. Если может быть найдена первообразная [math]F(x)[/math] подынтегральной функции, то по формуле Ньютона-Лейбница:
[math]\int_a^b{f(x)dx} = F(b) - F(a). [/math]
Если же первообразная не может быть найдена, то для вычисления интеграла прибегают к приближённым формулам, точность которых может быть сделана сколь угодно большой.
Приближённые методы вычисления определённого интеграла в большинстве случаев основаны на том, что определённый интеграл численно равен площади криволинейной трапеции, ограниченной кривой [math] y =f(x)[/math], сегментом [math] \left[ a,b \right] [/math] оси [math]Ox[/math] и вертикальными прямыми [math]x = a[/math] и [math]x = b[/math].
Идея данных методов заключается в приближении исходной кривой новой, достаточно близкой к старой, кривой. В качестве этой новой кривой подбирают такую, для которой площадь криволинейной трапеции подсчитывается просто. В зависимости от выбора новой кривой мы получим ту или иную приближённую формулу интегрирования.
Разбивая сегмент интегрирования на несколько достаточно малых частей, на каждом из полученных маленьких сегментов мы можем приблизить интегрируемую функцию прямой. Тем самым мы заменим криволинейную трапецию прямолинейной, формула площади которой проста для вычисления.
1.2 Математическое описание алгоритма
1.2.1 Метод трапеций
Будем рассматривать проблему вычисления значения определенного интеграла с некоторой заданной точностью [math] \epsilon [/math]:
[math]I(a,b) = \int_a^b{f(x)dx}[/math]
Пусть на отрезке [math] [a,b] [/math] задана равномерная сетка, содержащая [math] n+1 [/math] узел:
[math] x_{i} = a + \frac{(b - a)} {n} i, i = 0,...,n [/math]
Тогда, согласно методу трапеций, можно численно найти определенный интеграл от функции [math] f (x) [/math] на отрезке [math][a,b][/math]:
[math] \int_a^b{f(x)dx} = \frac{b - a}{n} \left( \frac{f(x_0)}{2} + \sum^{n-1}_{i=1} {f(x_i)} + \frac{f(x_n)}{2} \right)[/math]
Будем полагать значение [math] I [/math] найденным с точностью [math] \epsilon [/math], если выполнено условие:
[math] |I_{n_1} - I_{n_2}| \leq \epsilon |I_{n_2}|, n_1 \gt n_2, [/math] где [math] n_1 [/math] и [math] n_2 [/math] - количество узлов, образующих две разные сетки.
1.2.2 Метод рекурсивного деления
Метод трапеций обладает следующими недостатками:
- в некоторых точках значение функции будет вычисляться несколько раз;
- на всём интервале интегрирования используется равномерная сетка, тогда как число точек, необходимых для достижения заданной точности, зависит от вида функции и может сильно различаться на разных участках сегмента интегрирования.
Метод рекурсивного деления был придуман, чтобы избежать этих недостатков. Суть метода заключается в рекурсивном вызове себя до момента, пока мы не достигнем нужной точности: [math] I(a,b) = IntTrap(a, b, f(a), f(b)) = IntTrap(a, (b - a) / 2, f(a), f((b - a) / 2)) + IntTrap((b - a) / 2, b, f((b - a) / 2), f(b)) = ... [/math]
Однако можно заметить, что координаты концов обрабатываемых отрезков хранятся в программном стеке процесса [math]IntTrap() [/math], и недоступны программисту. Это является основной сложностью при построении параллельного алгоритма на основе метода рекурсивного деления.
1.2.3 Метод локального стека
Данный алгоритм использует массив данных, доступ к которым осуществляется по принципу стека - первым удаляется последний из добавленных элементов. Теперь у разных процессов есть возможность обрабатывать отрезки независимо друг от друга. В рассматриваемом алгоритме вместо стека можно было использовать и другие способы хранения заданий, например очередь. Стек выбран исключительно из соображений простоты реализации. Алгоритм локального стека можно считать наилучшим из перечисленных последовательных методов для разработки его параллельной версии.
1.3 Вычислительное ядро алгоритма
В схеме реализации будет явно видно, что алгоритм реализуется при помощи цикла, внутри которого происходит подсчет текущих частичных сумм и проверка достигнутой точности. Сложность данного алгоритма зависит от количества проходов по циклу линейно, поэтому можно считать, что тело этого цикла и является вычислительным ядром данного алгоритма.
1.4 Макроструктура алгоритма
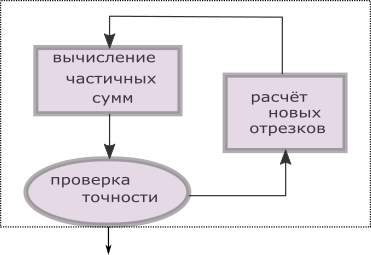
Как уже было замечено, алгоритм представляет собой три основные части, выполняющиеся в цикле. Сначала вычисляются частичные суммы на имеющемся отрезке, затем проверяется точность вычислений и, в случае, если точность недостаточна, вычисляются новые отрезки.
1.5 Схема реализации последовательного алгоритма
Будем считать, что описана функция double f( double x ), возвращающая значение f(x) интегрируемой функции f в точке x.
double f( double x );
int sp = 0; //указатель вершины стека
struct
{
double a;
double b;
double fa;
double fb;
double sab;
} stk[1000]; //массив структур, в которых хранятся отложенные значения. 1000 может быть заменена на необходимое число
//операции доступа к данным стека #define STACK_IS_NOT_FREE ( sp > 0 )
void PUT_INTO_STACK( double a, double b, double fa, double fb, double sab )
{
stk[sp].a = a;
stk[sp].b = b;
stk[sp].fa = fa;
stk[sp].fb = fb;
stk[sp].sab = sab;
++sp;
}
void GET_FROM_STACK( double& a, double& b, double& fa, double& fb, double& sab )
{
--sp;
a = stk[sp].a;
b = stk[sp].b;
fa = stk[sp].fa;
fb = stk[sp].fb;
sab = stk[sp].sab;
}
//основная функция
int IntTrap(a, b)
{
double I = 0; //значение интеграла
double fa = f( a ); //значение функции [math]y = f(x)[/math] в точке [math]a[/math]
double fb = f( b ); //значение функции [math]y = f(x)[/math] в точке [math]b[/math]
double fc = 0;
double c = 0; //середина отрезка интегрирования
double sab = 0; //
double sac = 0; //
double scb = 0; //
double sabc = 0; //переменные для подсчёта текущих сумм
sab = ( fa + fb ) * ( b - a ) / 2;
while( 1 )
{
c = ( a + b ) / 2;
fc = f( c );
sac = ( fa + fc ) * ( c - a ) / 2;
scb = ( fc + fb ) * ( b - c ) / 2;
sabc = sac + scb;
if( abs( sab - sabc ) > [math]\epsilon[/math] * abs ( sabc ) ) //[math]\epsilon[/math] - заданная точность
{
PUT_INTO_STACK( a, c, fa, fc, sac );
a = c;
fa = fc;
sab = scb;
}
else
{
I += sabc;
if( STACK_IS_NOT_FREE )
{
break;
}
GET_FROM_STACK( a, b, fa, fb, sab );
}
}
return I;
}
Работа со стеком происходит через операции доступа к данным. В основной функции в цикле происходит вычисление частичных сумм sac и scb, затем проверяется точность if( abs( sab - sacb ) >[math]\epsilon[/math] * abs ( sacb ) ). В случае достижения необходимой точности частичные суммы добавляются к значению интеграла I, если отрезков не осталось, то программа завершает работу, иначе из стека выгружается следующий отрезок. Если точность не достигнута, то правый полуотрезок загружается в стек, а левый полуотрезок устанавливается как текущий для следующей итерации цикла.
Когда в стеке не останется отрезков, это будет означать, что программа рассчитала все отрезки до точки a включительно, и возвращает значение I как приближённое значение интеграла.
1.6 Последовательная сложность алгоритма
Пусть для работы алгоритма было необходимо разбить отрезок [math] \left[a, b\right] [/math] на сегменты [math] \left[a=x_0 , x_1\right], \left[a=x_1 , x_2\right],... \left[a=x_{n-1} , x_n = b\right] [/math]. Так как каждый раз, когда нам приходится вычислять площадь трапеции на более коротком сегменте, мы делим отрезок пополам, получаем, что длина каждого отрезка равна [math] \left( x_i - x_{i - 1} \right) = \frac{b - a}{2^k} [/math] для некоторого натурального [math] k [/math].
Назовём глубиной метода максимальное [math] k [/math] из всех [math] k_i : \left( x_i - x_{i - 1} \right) = \frac{b - a}{2^{k_i}} [/math].
Очевидно, что для каждой функции [math] y [/math] и для каждой точности [math] \epsilon [/math] глубина алгоритма будет разной. То есть можно считать, что [math] k = k(f(x), \epsilon). [/math] Также понятно, что, если [math] k [/math]- глубина алгоритма при фиксированных [math] y [/math] и [math] \epsilon [/math], то максимально возможное количество полученных отрезков, для которых считалась частичная сумма, и количество точек на отрезке [math] \left[a, b\right] [/math] равны соответственно [math] 2^k [/math] и [math] 2^k + 1 [/math] при [math] k_i = k, i = 1,2,...,n [/math]. В этом худшем с точки зрения количества операций случае алгоритм прокрутит цикл while( 1 ) [math] 1 + 2 + 4 + ... + 2^k = (2^{k + 1}-1) [/math] раз.
Если не учитывать при расчёте сложности операции работы с памятью, а только сложения/вычитания и умножения*деления, получим, что за каждый выполненный цикл while( 1 ) алгоритм выполняет 7 сложений и 6 умножений. Итого получаем в худшем случае [math] 7*2^k [/math] сложений и [math] 6*2^k [/math] умножений. Кроме этого, алгоритм посчитает значение [math] f(x) [/math] в [math] n+1 [/math] точках. При этом понятно, что [math] k \leq log(n). [/math]
Получаем, что при разбиении исходного отрезка на [math] n [/math] подотрезков получаем глубину алгоритма [math] k \leq log(n) [/math] и сложность алгоритма [math] O\left( n + 2^{log n} \right) = O\left( n + n \right) = O\left( n \right) [/math].
При этом из всего вышесказанного сразу видно, что при достаточном количестве вычислительных ресурсов распараллеливания высота ярусно-параллельной формы параллельной программы будет равна глубине [math] k \leq log(n), [/math], а ширина будет не больше, чем количество отрезков [math] n. [/math]
1.7 Информационный граф
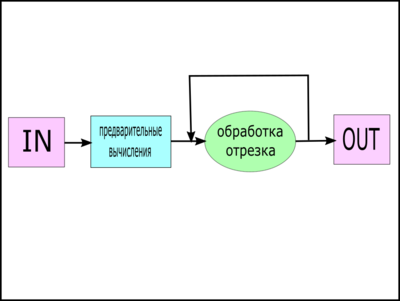
На Рис.1 изображена макроструктура алгоритма. На вход алгоритма подаётся функция, границы отрезка интегрирования и нужная точность. В предварительных вычислениях задаются границы первого отрезка и значения функции в них. Далее запускается операция обработки отрезка, в случае недостаточной точности повторяющаяся для двух подотрезков (и так далее, пока не будет достигнута нужная точность), на выход алгоритм выдаёт приближённое значение интеграла на заданном отрезке с необходимой точностью.
Рассмотрим процедуру обработки отрезка подробнее.
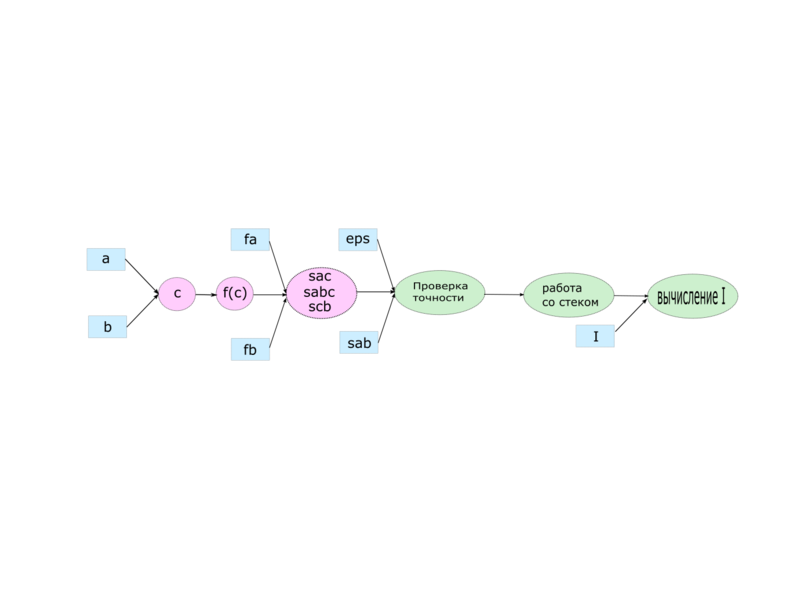
На Рис.2 изображён информационный граф алгоритма обработки отрезка. Синими прямоугольниками изображены входные данные итерации цикла, внутри подписаны имена данных. Кругами изображены операции вычисления переменных, имена которых указаны внутри кругов. Зелёными овалами изображены прочие операции, выполняемые алгоритмом. После операции проверки точности алгоритм загружает правый отрезок в стек, а левый настраивает на дальнейшую обработку, если точность не достигнута, иначе загружает новый отрезок из стека. Затем происходит суммирование текущей частичной суммы с полученными ранее. При отсутствии отрезков в стеке итерация завершается.
1.8 Ресурс параллелизма алгоритма
Представленный алгоритм обладает хорошим ресурсом параллелизма. В самом деле, пусть в нашем распоряжении есть доступный всем параллельным процессам список отрезков интегрирования, организованный в виде стека. Назовём его глобальным стеком. Предположим, что перед запуском параллельных процессов в глобальный стек помещается единственная запись - координаты концов отрезка интегрирования - в дальнейшем - "отрезок". Тогда возможно реализовать следующую схему алгоритма, выполняемую каждым из параллельных процессов:
Пока в глобальном стеке есть отрезки:
- взять один отрезок из глобального стека;
- выполнить алгоритм локального стека, выполняя при записи в локальный стек следующие операции:
- если в локальном стеке есть несколько отрезков, а в глобальном стеке отрезки отсутствуют, то
- переместить часть отрезков из локального стека в глобальный;
- по исчерпании локального стека добавить полученную частичную сумму к общему значению интеграла.
- если в локальном стеке есть несколько отрезков, а в глобальном стеке отрезки отсутствуют, то
1.9 Входные и выходные данные алгоритма
Входные данные:
- функция [math] y = f(x)[/math];
- точность [math] \epsilon [/math];
- границы отрезка интегрирования [math] a, b.[/math]
Формально оценить объём входных данных не получится, так как функция может иметь любой вид представления. Кроме функции, на вход подаётся три вещественных числа, их объём - [math] 3 * sizeof( double ) [/math].
Выходные данные:
- число [math]I [/math], приближённо равное [math] \int_a^b{f(x)dx}[/math] с точностью [math] \epsilon [/math].
На выход алгоритм выдаёт одно вещественное число, его объём - [math] sizeof( double ) [/math].
1.10 Свойства алгоритма
Алгоритм обладает большой вычислительной мощностью. Кроме того, у него имеется большой потенциал для распараллеливания.
Алгоритм не обладает свойством детерминированности, так как в зависимости от специфических свойств графика входных функций может вести себя для них совершенно по-разному.
Соотношение последовательной и параллельной сложности алгоритма высоко и равно приблизительно [math] \frac{n}{log(n)} [/math].
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.
Для распараллеливания программы был выбран алгоритм геометрического параллелизма. Весь отрезок интегрирования делился на равные части, количество которых было равно количеству процессов. Далее каждый процесс выполнял функцию [math] IntTrap(a_i, b_i) [/math] для своего отрезка [math] [ a_i, b_i ] [/math] независимо от других процессов. При таком алгоритме мало затрат на обмен данными между процессами, поэтому было решено воспользоваться только средствами библиотеки MPI.
Для оценки масштабируемости были произведены запуски на 1, 2, 4, 8, 16, 32, 48, 64, 80, 96, 112 и 128 процессах. Кроме того, для каждого количества процессов были произведены запуски при разной точности вычисления интеграла, от [math]10^{-5} [/math] до [math]10^{-7} [/math].
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
На данный момент реализация алгоритма локального стека была указана только в книге Якобовского М.В., Кульковой Е.Ю. "Решение задач на многопроцессорных вычислительных системах с разделяемой памятью."
3 Литература
- Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», 1972. 640 с.
- Якобовский М.В., Кулькова Е.Ю. Решение задач на многопроцессорных вычислительных системах с разделяемой памятью. - М.: СТАНКИН, 2004. – 30 c.