Участник:Dlin/Алгоритм концептуальной кластеризации COBWEB: различия между версиями
Dlin (обсуждение | вклад) |
Dlin (обсуждение | вклад) |
||
| Строка 17: | Строка 17: | ||
Алгоритм COBWEB – классический метод инкрементальной концептуальной кластеризации. Он создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт и содержит вероятностное описание этого концепта, которое включает в себя вероятность принадлежности концепта к данному узлу и условные вероятности вида: <math>P(A_{j}={\upsilon}_{ij}|C_k)</math>, где <math>A_{i}={\upsilon}_{ij} </math> – пара атрибут-значение, <math>C_{k}</math> – класс концепта. | Алгоритм COBWEB – классический метод инкрементальной концептуальной кластеризации. Он создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт и содержит вероятностное описание этого концепта, которое включает в себя вероятность принадлежности концепта к данному узлу и условные вероятности вида: <math>P(A_{j}={\upsilon}_{ij}|C_k)</math>, где <math>A_{i}={\upsilon}_{ij} </math> – пара атрибут-значение, <math>C_{k}</math> – класс концепта. | ||
Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории – прирост ожидаемого числа корректных предположений о значениях атрибутов при знании об их принадлежности к определённой категории относительно ожидаемого числа корректных предположений о значениях атрибутов без этого знания. | Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории – прирост ожидаемого числа корректных предположений о значениях атрибутов при знании об их принадлежности к определённой категории относительно ожидаемого числа корректных предположений о значениях атрибутов без этого знания. | ||
| − | |||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| Строка 56: | Строка 55: | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| − | + | cobweb(Node, Instance) | |
| − | + | Begin | |
| − | if | + | if узел Node - это лист, then |
| − | + | begin | |
| − | + | создать два дочерних узла L1 и L2 для узла Node; | |
| − | + | задать для узла L1 те же вероятности, что и для узла Node; | |
| + | инициализировать вероятности для узла L2 соответствующими значениями объекта Instance; | ||
| + | добавить Instance к Node, обновив вероятности для узла Node ; | ||
| + | end | ||
else | else | ||
| − | + | begin | |
| − | + | добавить Instance к Node, обновив вероятности для узла Node; | |
| − | + | для каждого дочернего узла С узла Node вычислить полезность категории при отнесении экземпляра Instance к категории С; | |
| − | + | пусть S1 - значение полезности для наилучшей классификации C1; | |
| − | end | + | пусть S2 - значение для второй наилучшей классификации C2; |
| − | + | пусть S3 - значение полезности для отнесения экземпляра к новой категории; | |
| − | + | пусть S4 - значение для слияния C1 и C2 в одну категорию; | |
| − | + | пусть S5 - значение для разделения C1 (замены дочерними категориями); | |
| − | + | end | |
| − | + | if S1 - максимальное значение CU, then | |
| − | + | cobweb(C1, Instance) %отнести экземпляр к C1 | |
| − | + | else | |
| − | + | if S3 - максимальное значение CU, then | |
| − | + | инициализировать вероятности для новой категории Cm значениями Instance | |
| − | + | else | |
| − | + | if S4 - максимальное значение CU, then | |
| − | + | begin | |
| − | + | пусть Cm - результат слияния C1 и C2; | |
| + | cobweb(Cm, Instance); | ||
| + | end | ||
| + | else | ||
| + | if S5 - максимальное значение CU, then | ||
| + | begin | ||
| + | разделить C1; % Cm - новая категория | ||
| + | cobweb(Cm, Instance) | ||
| + | end; | ||
| + | end | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| Строка 94: | Строка 105: | ||
=== Информационный граф === | === Информационный граф === | ||
| + | [[File:cobweb_graph.png|thumb|450 px|Выбор операции]] | ||
| + | |||
| + | На данном информационном графе изображен алгоритм выбора нужного действия при добавлении нового объекта в дерево классификации. А именно функция COBWEB, которая во время выполнения программы вызывается рекурсивно. | ||
| + | |||
| + | Входными данными являются текущий объект, который надо добавить, а также один из узлов дерева. На первой итерации это корень дерева. | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| Строка 101: | Строка 117: | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| − | На вход алгоритм принимает множество объектов, представляемых в виде бинарных списков, характеризуемых набором свойств. | + | На вход алгоритм принимает множество объектов, представляемых в виде бинарных списков, характеризуемых набором свойств. Результатом работы алгоритма является построенное дерево классификации, листья которого представляют собой различные классы объектов и содержат сами объекты принадлежащие данному классу. |
=== Свойства алгоритма === | === Свойства алгоритма === | ||
Версия 20:43, 1 декабря 2016
Основные авторы описания: Линь Данил (1.1-1.10, 2.7)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм COBWEB был впервые предложен профессором университета Вандербильта, Douglas H. Fisher в 1987 году и относится к классу концептуальных алгоритмов кластеризации.
Кластеризацией называется подход к описанию данных, в котором наиболее схожие данные объединяются в группы(кластеры). Кластеризация является распространенным подходом для анализа данных и используется во многих сферах научной деятельности, таких как машинное обучение, анализ данных, распознавание шаблонов, анализ изображений и биоинформатика.
Кластеризация представляет собой комбинирование рассматриваемых объектов так, чтобы каждая группа объектов обладала схожим свойством. В общем случае кластеризация характеризуются следующими критериями: - Каждая группа или кластер однородны; объекты, принадлежащие одной группе имеют схожие свойства; - Каждая группа или кластер отличаются от других кластеров т.е. объекты, принадлежащие одному кластеру, должны отличатся от объектов других кластеров
В отличие от традиционной кластеризации, которая обнаруживает группы схожих объектов на основе меры сходства между ними, концептуальная кластеризация определяет кластеры как группы объектов, относящейся к одному классу или концепту – определённому набору пар атрибут-значение.
Алгоритм COBWEB – классический метод инкрементальной концептуальной кластеризации. Он создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт и содержит вероятностное описание этого концепта, которое включает в себя вероятность принадлежности концепта к данному узлу и условные вероятности вида: [math]P(A_{j}={\upsilon}_{ij}|C_k)[/math], где [math]A_{i}={\upsilon}_{ij} [/math] – пара атрибут-значение, [math]C_{k}[/math] – класс концепта. Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории – прирост ожидаемого числа корректных предположений о значениях атрибутов при знании об их принадлежности к определённой категории относительно ожидаемого числа корректных предположений о значениях атрибутов без этого знания.
1.2 Математическое описание алгоритма
В алгоритме COBWEB реализовано вероятностное представление категорий. Принадлежность категории определяется не набором значений каждого свойства объекта, а вероятностью появления значения. Например, [math]P(A_{j}={\upsilon}_{ij}|C_k)[/math] - это условная вероятность, с которой свойство [math]A_{j}[/math], принимает значение [math]{\upsilon}_{ij}[/math], если объект относится к категории [math]C_{k}[/math]. Для каждой категории в иерархии определены вероятности вхождения всех значений каждого свойства. При предъявлении нового экземпляра система COBWEB оценивает качество отнесения этого примера к существующей категории и модификации иерархии категорий в соответствии с новым представителем. Критерием оценки качества классификации является полезность категории (category utility), которая учитывает влияние категорий базового уровня и другие аспекты структуры человеческих категорий.
1.3 Вычислительное ядро алгоритма
Чтобы встроить новый объект в дерево классификации, алгоритм COBWEB итеративно проходит всё дерево в поисках «лучшего» узла, к которому отнести этот объект. Выбор узла осуществляется на основе помещения объекта в каждый узел и вычисления полезности категории получившегося среза. Также вычисляется полезность категории для случая, когда объект относится к вновь создаваемому узлу. В итоге объект относится к тому узлу, для которого полезность категории больше.
Критерий полезности категории максимизирует вероятность того, что два объекта, отнесенные к одной категории, имеют одинаковые значения свойств и значения свойств для объектов из различных категорий отличаются. Полезность категории определяется формулой:
[math] CU = \sum_{k} { \sum_{i} { \sum_{j} { {P(A={\upsilon}_{ij}|C_k)} {({P(C_k | A={\upsilon}_{ij})} P(A={\upsilon}_{ij})} } } } [/math]
Значения суммируются по всем категориям [math]C_{k}[/math], всем свойствам [math]A_{j}[/math] и всем значениям свойств [math]{\upsilon}_{ij}[/math]. Значение [math]P(A_{j}={\upsilon}_{ij}|C_k)[/math] называется предсказуемостью (predictability). Это вероятность того, что объект, для которого свойство [math]A_{j}[/math] - принимает значение [math]{\upsilon}_{ij}[/math], относится к категории [math]C_k[/math]. Чем выше это значение, тем вероятнее, что свойства двух объектов, отнесенных к одной категории, имеют одинаковые значения. Величина [math]P(C_k | A={\upsilon}_{ij})[/math] называется предиктивностью (predictiveness). Это вероятность того, что для объектов из категории [math]C_k[/math] свойство [math]A_j[/math] принимает значение [math]{\upsilon}_{ij}[/math]. Чем больше эта величина, тем менее вероятно, что для объектов, не относящихся к данной категории, это свойство будет принимать указанное значение. Значение [math]P(A={\upsilon}_{ij}[/math] - это весовой коэффициент, усиливающий влияние наиболее распространенных свойств. Благодаря совместному учету этих значений высокая полезность категории означает высокую вероятность того, что объекты из одной категории обладают одинаковыми свойствами, и низкую вероятность наличия этих свойств у объектов из других категорий.
После некоторых преобразований (Байеса в частности) и некоторых агрументированных изменений мы получаем более правильную формулу:
[math]CU= \frac{ \sum_{k=1}^N {P(A={\upsilon}_{ij}|C_k)} \sum_{j} { \sum_{i} {({P(C_k | A={\upsilon}_{ij})}^2 - {P(A={\upsilon}_{ij})}^2)}}}{N} [/math]
где N -число категорий.
1.4 Макроструктура алгоритма
Алгоритм COBEWB создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт. Каждый концепт представляется в виде набора объектов, а объекты являтются бинарными списками. В качестве примера возьмем задачу отнесения особи к определенной биологической группе. Рассмотрим концепт [math]C_1[/math], включающий в себя 4 объекта:
[1 0 1][0 1 1][0 1 0][0 1 1]
Признаки объекта могут иметь следующий смысл: [мужского_пола, птица, ведущий_ночной_образ_жизни]. Концепт характеризуется целочисленным списком, в котором хранятся суммы соответствующих значений объектов. Для [math]C_1[/math] данный счетчик будет [1 3 3], что означает что биологическая группа включает в себя одну особь мужского пола, три птицы и три особи ведущие ночной образ жизни. Данный счетчик является основанием для вероятностного описания конкретного концепта. Таким образом, вероятность того, что особь, принадлежащая концепту [math]C_1[/math], мужского пола равна [math]1/4 = 0.25[/math], а концепт в целом можно характеризовать как [.25 .75 .75]. Рисунок справа иллюстрирует дерево классификации для 5 концептов. [math]C_0[/math] - корневой концепт, включающий в себя все объекты из набора данных. [math]C_1[/math] и [math]C_2[/math] - концепты-потомки, объединяющие 4 и 6 объектов соответственно. [math]C_2[/math] в свою очередь, является концептом-родителем для [math]C_3[/math], [math]C_4[/math], [math]C_5[/math].
1.5 Схема реализации последовательного алгоритма
cobweb(Node, Instance)
Begin
if узел Node - это лист, then
begin
создать два дочерних узла L1 и L2 для узла Node;
задать для узла L1 те же вероятности, что и для узла Node;
инициализировать вероятности для узла L2 соответствующими значениями объекта Instance;
добавить Instance к Node, обновив вероятности для узла Node ;
end
else
begin
добавить Instance к Node, обновив вероятности для узла Node;
для каждого дочернего узла С узла Node вычислить полезность категории при отнесении экземпляра Instance к категории С;
пусть S1 - значение полезности для наилучшей классификации C1;
пусть S2 - значение для второй наилучшей классификации C2;
пусть S3 - значение полезности для отнесения экземпляра к новой категории;
пусть S4 - значение для слияния C1 и C2 в одну категорию;
пусть S5 - значение для разделения C1 (замены дочерними категориями);
end
if S1 - максимальное значение CU, then
cobweb(C1, Instance) %отнести экземпляр к C1
else
if S3 - максимальное значение CU, then
инициализировать вероятности для новой категории Cm значениями Instance
else
if S4 - максимальное значение CU, then
begin
пусть Cm - результат слияния C1 и C2;
cobweb(Cm, Instance);
end
else
if S5 - максимальное значение CU, then
begin
разделить C1; % Cm - новая категория
cobweb(Cm, Instance)
end;
end
1.6 Последовательная сложность алгоритма
Сложность алгоритма зависит не только от количества атрибутов, но и от количества их возможных значений. Данный факт, а также сложная структура дерева, получаемая после процедуры обучения, делает невозможным оценку сложности алгоритма в целом, однако сложность функции полезности категории поддается оценке:
[math] O(|C|*|A|*|V|*|O|)[/math], где
- [math]|C|[/math] - количество классов в срезе
- [math]|A|[/math] - количество аттрибутов объекта
- [math]|V|[/math] - количество возможных значений
- [math]|O|[/math] - количество объектов.
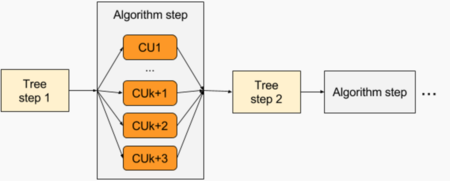
1.7 Информационный граф
На данном информационном графе изображен алгоритм выбора нужного действия при добавлении нового объекта в дерево классификации. А именно функция COBWEB, которая во время выполнения программы вызывается рекурсивно.
Входными данными являются текущий объект, который надо добавить, а также один из узлов дерева. На первой итерации это корень дерева.
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
На вход алгоритм принимает множество объектов, представляемых в виде бинарных списков, характеризуемых набором свойств. Результатом работы алгоритма является построенное дерево классификации, листья которого представляют собой различные классы объектов и содержат сами объекты принадлежащие данному классу.
1.10 Свойства алгоритма
Алгоритм COBWEB достаточно эффективен и выполняет кластеризацию на разумное число классов. Поскольку в нем используется вероятностное представление принадлежности, получаемые категории являются гибкими и робастными. Кроме того, в нем проявляется эффект категорий базового уровня, поддерживается прототипирование и учитывается степень принадлежности. Он основан не на классической логике, а, подобно методам теории нечетких множеств, учитывает "неопределенность" категоризации как необходимый компонент обучения и рассуждений в гибкой и интеллектуальной манере. Однако COBWEB имеет ряд ограничений. Во-первых, он предполагает, что распределения вероятностей значений различных атрибутов статистически независимы друг от друга. Однако это предположение не всегда верно, потому как часто между значениями атрибутов существует корреляция. Во-вторых, вероятностное представление кластеров делает очень сложным их обновление, особенно в том случае, когда атрибуты имеют большое число возможных значений.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- Working python implementation of COBWEB библиотека реализации алгоритмов COBWEB и COBWEB/3 для языка Python.
3 Литература
[1] Fisher D. Knowledge Acquisition Via Incremental Conceptual Clustering, 1987. – P. 142–153. - http://link.springer.com/article/10.1007/BF00114265
[2] Методы и средства анализа данных - Алгоритм Cobweb: http://bourabai.ru/tpoi/analysis6.htm#.D0.90.D0.BB.D0.B3.D0.BE.D1.80.D0.B8.D1.82.D0.BC_Cobweb
[3] МОДЕЛЬ И МЕТОД КОНЦЕПТУАЛЬНОЙ КЛАСТЕРИЗАЦИИ ОБЪЕКТОВ, ХАРАКТЕРИЗУЕМЫХ НЕЧЕТКИМИ ПАРАМЕТРАМИ // Фундаментальные исследования. – 2014. – № 9 (часть 5) – С. 993-997 - http://www.fundamental-research.ru/ru/article/view?id=35003
[4] Обзор алгоритмов кластеризации числовых пространств данных: https://habrahabr.ru/post/164417/