Участник:Prokopenko/Алгоритм построения бифуркационной диаграммы динамической системы: различия между версиями
| Строка 81: | Строка 81: | ||
<math>N</math> - количество узлов сетки значений параметров; | <math>N</math> - количество узлов сетки значений параметров; | ||
| − | <math> | + | <math>t_{stabilize}</math> - номер кванта времени, после которого считаем систему стабильной; |
| − | <math> | + | <math>t_{print}</math> - номер кванта времени, после которого прекращается вывод результатов; |
<math>rmin, rmax</math> - краевые значения параметров; | <math>rmin, rmax</math> - краевые значения параметров; | ||
Версия 21:49, 30 ноября 2016
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм предназначен для графического изображения смены возможных динамических режимов системы при изменении значений бифуркационных параметров.
1.2 Математическое описание алгоритма
Рассматривается динамическая система: [math]u_{t+1} = f(u_t, \ldots, u_{t - k}, r_0, \ldots, r_l), u_0 = u^0 = const, \ldots, u_k = u^k = const, r_0 = const \gt 0, \ldots, r_l = const \gt 0[/math]. Для построения бифуркационной диаграммы системы необходимо:
1. Выбрать подпространство значений параметров, на котором будет рассматриваться поведение системы.
2. Для каждого набора значений параметров вычислить [math]N[/math] последовательных состояний системы, начиная с начального состояния, где [math]N[/math] - достаточно большое число квантов времени. Этот шаг выполняется для стабилизации системы, в случае если для данного значения параметров система не ведет себя хаотично (имеет устойчивую точку, цикл, аттрактор и т.п.).
3. Вычислить еще [math]K[/math] состояний системы, начиная с [math]N[/math]-го состояния и вывести соответствующие результаты вместе со значениями параметров в файл. Чем больше число [math]K[/math], тем точнее будет бифуркационная диаграмма.
4. Отобразить полученные результаты графически.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является цикл прохода по сетке рассматриваемых значений параметров. На каждой итерации внешнего цикла проходятся два цикла, последовательно вычисляющие последующие состояния системы на основании рассматриваемых значений параметров и необходимого количества предыдущих состояний системы. В первом цикле рассчитываются [math]N[/math] состояний системы без вывода полученных данных, где [math]N[/math] — достаточно большое число итераций, необходимое для того, чтобы система стабилизировалась. Во втором цикле рассчитываются следующие [math]K[/math] состояний системы, полученные значения выводятся. Здесь [math]K[/math] задается исходя из желаемого качества отображения бифуркационной диаграммы.
1.4 Макроструктура алгоритма
Как уже сказано в описании ядра алгоритма, основную часть метода составляют вычисления состояний системы в зависимости от значений параметров и характерного для рассматриваемой системы числа предыдущих состояний.
1.5 Схема реализации последовательного алгоритма
Рассмотрим фрагмент реализации алгоритма на c++ для системы [math]u_t = ru_{t - 1}(1 - u_{t-1}), u_0 = u^0[/math] на области изменения параметра [math]0\leqslant r \leqslant 4[/math].
double system_func(double u0, double r) //задаем систему
{
return r*u0*(1 - u0);
}
int main()
{
int t_stabilize = 900; //номер кванта времени, после которого считаем, что система стабильна
int t_print = 1000; //номер кванта времени, на котором преращаем вывод полученных точек для системы при конкретном значении параметра
double rmin = 0; //минимальное рассматриваемое значение параметра
double rmax = 4; //максимальное рассматриваемое значение параметра
double r;
double u0;
int N = 1024;
double coef = (rmax - rmin)/N; //расчет шага сетки
int i;
double t;
double u;
for (i = 1; i <= N; i++)
{
r = rmin + coef*i; //взятие нового значения параметра на сетке
u0 = 0.1; //взятие начального состояния системы
u = u0;
for (t = 1; t <= t_stabilize; t++) //расчет последовательных состояний системы до момента стабилизации
{
u = system_func(u0, r); //расчет следующего состояния системы
u0 = u; //фиксация предыдущего состояния системы для следующей итерации
}
for (t = t_stabilize + 1; t <= t_print; t++) //расчет заданного количества состояний системы после момент стабилизации для вывода
{
u = system_func(u0, r);
cout << r << ' ' << u << end; //вывод значения параметра и состояния системы для последующей визуализации
u0 = u;
}
}
}
1.6 Последовательная сложность алгоритма
Рассмотрим сложность последовательной реализации ядра алгоритма в терминах арифметических операций: сложений/вычитаний и умножений/делений.
Пусть на сетке значений параметра [math]P[/math] узлов, система стабилизируется за [math]N[/math] квантов времени, выводится [math]K[/math] состояний системы. Пусть для вычисления следующего значения функции нужно привести [math]m[/math] умножений/делений и [math]a[/math] сложений/вычитаний. Тогда сложность последовательной реализации составляет [math]P(1 +(N + K)m)[/math] умножений/делений и [math]P(1 + (N + K)a)[/math] сложений/вычитаний.
1.7 Информационный граф
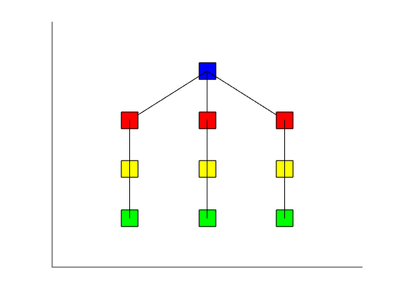
Синим цветом обозначен блок инициализации начальных условий (например, шага сетки), красным - взятие текущего значения параметров на сетке, желтым - блок стабилизации системы (проход первого внутреннего цикла), зеленым - расчет последующих состояний системы с выводом (проход второго внутреннего цикла).
1.8 Ресурс параллелизма алгоритма
Ресурс параллелизма алгоритма заключается в информационной независимости итераций внешнего цикла. Таким образом можно разделить внешний цикл по значениям параметра на разные процессы.
1.9 Входные и выходные данные алгоритма
Входные данные:
[math]N[/math] - количество узлов сетки значений параметров;
[math]t_{stabilize}[/math] - номер кванта времени, после которого считаем систему стабильной;
[math]t_{print}[/math] - номер кванта времени, после которого прекращается вывод результатов;
[math]rmin, rmax[/math] - краевые значения параметров;
Функция, описывающая поведение системы.
Выходные данные:
Наборы, представляющие собой состояние системы и соответствующие значения параметров.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
Вторая часть описания алгоритмов в рамках AlgoWiki рассматривает все составные части процесса их реализации. Рассматривается как последовательная реализация алгоритма, так и параллельная. Описывается взаимосвязь свойств программ, реализующих алгоритм, и особенностей архитектуры компьютера, на которой они выполняются. Исследуется работа с памятью, локальность данных и вычислений, описывается масштабируемость и эффективность параллельных программ, производительность компьютеров, достигаемая на данной программе. Обсуждаются особенности реализации для разных классов архитектур компьютеров, приводятся ссылки на реализации в существующих библиотеках.
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Задача данного раздела - показать пределы масштабируемости алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование сильной и слабой масштабируемости алгоритма и его реализаций.
Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).
Ключевой момент данного раздела заключается в том, чтобы показать реальные параметры масштабируемости программы для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи [1]. При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.
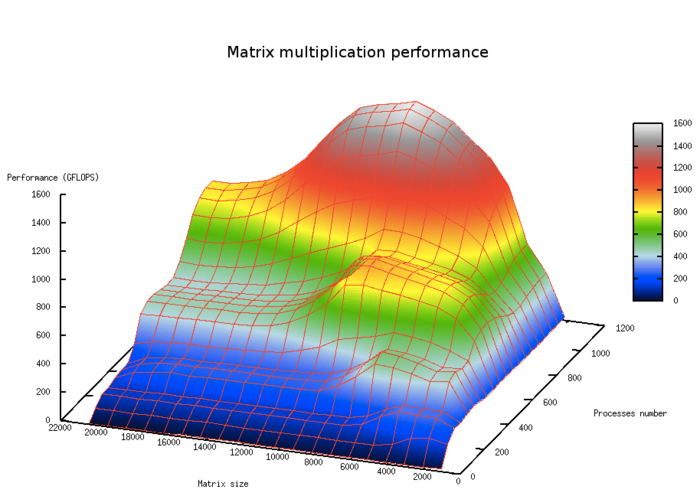
На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Для многих пар алгоритм+компьютер уже созданы хорошие реализации, которыми можно и нужно пользоваться на практике. Данный раздел предназначен для того, чтобы дать ссылки на основные существующие последовательные и параллельные реализации алгоритма, доступные для использования уже сейчас. Указывается, является ли реализация коммерческой или свободной, под какой лицензией распространяется, приводится местоположение дистрибутива и имеющихся описаний. Если есть информация об особенностях, достоинствах и/или недостатках различных реализаций, то это также нужно здесь указать. Хорошими примерами реализации многих алгоритмов являются MKL, ScaLAPACK, PETSc, FFTW, ATLAS, Magma и другие подобные библиотеки.
- ↑ Антонов А.С., Теплов А.М. О практической сложности понятия масштабируемости параллельных программ// Высокопроизводительные параллельные вычисления на кластерных системах (HPC 2014): Материалы XIV Международной конференции -Пермь: Издательство ПНИПУ, 2014. С. 20-27.