Участник:Prokopenko/Алгоритм построения бифуркационной диаграммы динамической системы: различия между версиями
| Строка 144: | Строка 144: | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| − | + | Последовательные реализации: | |
| + | [http://www.physics.sfsu.edu/~mstevens/chaos/bifur2.htm] - построение бифуркационной диаграммы для хаотического маятника. | ||
| + | [https://www.math.utah.edu/~jasonu/code/] - построение бифуркационной диаграммы логистического отображения. | ||
Версия 22:13, 30 ноября 2016
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм предназначен для графического изображения смены возможных динамических режимов системы при изменении значений бифуркационных параметров.
1.2 Математическое описание алгоритма
Рассматривается динамическая система: [math]u_{t+1} = f(u_t, \ldots, u_{t - k}, r_0, \ldots, r_l), u_0 = u^0 = const, \ldots, u_k = u^k = const, r_0 = const \gt 0, \ldots, r_l = const \gt 0[/math]. Для построения бифуркационной диаграммы системы необходимо:
1. Выбрать подпространство значений параметров, на котором будет рассматриваться поведение системы.
2. Для каждого набора значений параметров вычислить [math]N[/math] последовательных состояний системы, начиная с начального состояния, где [math]N[/math] - достаточно большое число квантов времени. Этот шаг выполняется для стабилизации системы, в случае если для данного значения параметров система не ведет себя хаотично (имеет устойчивую точку, цикл, аттрактор и т.п.).
3. Вычислить еще [math]K[/math] состояний системы, начиная с [math]N[/math]-го состояния и вывести соответствующие результаты вместе со значениями параметров в файл. Чем больше число [math]K[/math], тем точнее будет бифуркационная диаграмма.
4. Отобразить полученные результаты графически.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является цикл прохода по сетке рассматриваемых значений параметров. На каждой итерации внешнего цикла проходятся два цикла, последовательно вычисляющие последующие состояния системы на основании рассматриваемых значений параметров и необходимого количества предыдущих состояний системы. В первом цикле рассчитываются [math]N[/math] состояний системы без вывода полученных данных, где [math]N[/math] — достаточно большое число итераций, необходимое для того, чтобы система стабилизировалась. Во втором цикле рассчитываются следующие [math]K[/math] состояний системы, полученные значения выводятся. Здесь [math]K[/math] задается исходя из желаемого качества отображения бифуркационной диаграммы.
1.4 Макроструктура алгоритма
Как уже сказано в описании ядра алгоритма, основную часть метода составляют вычисления состояний системы в зависимости от значений параметров и характерного для рассматриваемой системы числа предыдущих состояний.
1.5 Схема реализации последовательного алгоритма
Рассмотрим фрагмент реализации алгоритма на c++ для системы [math]u_t = ru_{t - 1}(1 - u_{t-1}), u_0 = u^0[/math] на области изменения параметра [math]0\leqslant r \leqslant 4[/math].
double system_func(double u0, double r) //задаем систему
{
return r*u0*(1 - u0);
}
int main()
{
int t_stabilize = 900; //номер кванта времени, после которого считаем, что система стабильна
int t_print = 1000; //номер кванта времени, на котором преращаем вывод полученных точек для системы при конкретном значении параметра
double rmin = 0; //минимальное рассматриваемое значение параметра
double rmax = 4; //максимальное рассматриваемое значение параметра
double r;
double u0;
int N = 1024;
double coef = (rmax - rmin)/N; //расчет шага сетки
int i;
double t;
double u;
for (i = 1; i <= N; i++)
{
r = rmin + coef*i; //взятие нового значения параметра на сетке
u0 = 0.1; //взятие начального состояния системы
u = u0;
for (t = 1; t <= t_stabilize; t++) //расчет последовательных состояний системы до момента стабилизации
{
u = system_func(u0, r); //расчет следующего состояния системы
u0 = u; //фиксация предыдущего состояния системы для следующей итерации
}
for (t = t_stabilize + 1; t <= t_print; t++) //расчет заданного количества состояний системы после момент стабилизации для вывода
{
u = system_func(u0, r);
cout << r << ' ' << u << end; //вывод значения параметра и состояния системы для последующей визуализации
u0 = u;
}
}
}
1.6 Последовательная сложность алгоритма
Рассмотрим сложность последовательной реализации ядра алгоритма в терминах арифметических операций: сложений/вычитаний и умножений/делений.
Пусть на сетке значений параметра [math]P[/math] узлов, система стабилизируется за [math]N[/math] квантов времени, выводится [math]K[/math] состояний системы. Пусть для вычисления следующего значения функции нужно привести [math]m[/math] умножений/делений и [math]a[/math] сложений/вычитаний. Тогда сложность последовательной реализации составляет [math]P(1 +(N + K)m)[/math] умножений/делений и [math]P(1 + (N + K)a)[/math] сложений/вычитаний.
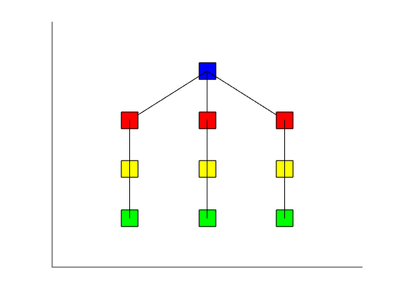
1.7 Информационный граф
Синим цветом обозначен блок инициализации начальных условий (например, шага сетки), красным - взятие текущего значения параметров на сетке, желтым - блок стабилизации системы (проход первого внутреннего цикла), зеленым - расчет последующих состояний системы с выводом (проход второго внутреннего цикла).
1.8 Ресурс параллелизма алгоритма
Ресурс параллелизма алгоритма заключается в информационной независимости итераций внешнего цикла. Таким образом можно разделить внешний цикл по значениям параметра на разные процессы.
1.9 Входные и выходные данные алгоритма
Входные данные:
[math]N[/math] - количество узлов сетки значений параметров;
[math]t_{stabilize}[/math] - номер кванта времени, после которого считаем систему стабильной;
[math]t_{print}[/math] - номер кванта времени, после которого прекращается вывод результатов;
[math]rmin, rmax[/math] - краевые значения параметров;
Функция, описывающая поведение системы.
Выходные данные:
Наборы, представляющие собой состояние системы и соответствующие значения параметров.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Рассматривается система [math]u_t = ru_{t - 1}(1 - u_{t-1}), u_0 = u^0[/math] на области изменения параметра [math]0\leqslant r \leqslant 4[/math], на сетке 1024 узла, система стабилизируется на 900 кванте времени, расчет и вывод останавливается на 1000 кванте времени.
| Число процессов | Время (с) |
|---|---|
| 128 | 0.234 |
| 64 | 0.24 |
| 32 | 0.248 |
| 16 | 0.254 |
| 8 | 0.272 |
| 4 | 0.29 |
| 2 | 0.323 |
| 1 | 0.34 |
Очевидно, что система плохо масштабируема за счет того, что вывод результатов довольно трудоемкий, но осуществлять его приходится часто.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Последовательные реализации: [1] - построение бифуркационной диаграммы для хаотического маятника. [2] - построение бифуркационной диаграммы логистического отображения.