Поиск в ширину (BFS): различия между версиями

[непроверенная версия]

Версия 12:33, 11 июля 2017

Содержание

1 Свойства и структура алгоритма
2 Программная реализация алгоритма
3 Литература

1 Свойства и структура алгоритма

Поиск в ширину (англ. Breadth-First Search, BFS) позволяет вычислить кратчайшие расстояния (в терминах количества рёбер) от выделенной вершины ориентированного графа до всех остальных вершин, и/или построить корневое направленное дерево, расстояния в котором совпадают с расстояниями в исходном графе. Алгоритм решает задачу поиска кратчайшего пути на графе в случае одинаковых весов рёбер. Впервые алгоритм поиска в ширину описан в работах Мура^[1] и Ли^[2].

1.1 Общее описание алгоритма

1.2 Математическое описание алгоритма

1.3 Вычислительное ядро алгоритма

1.4 Макроструктура алгоритма

1.5 Схема реализации последовательного алгоритма

1.6 Последовательная сложность алгоритма

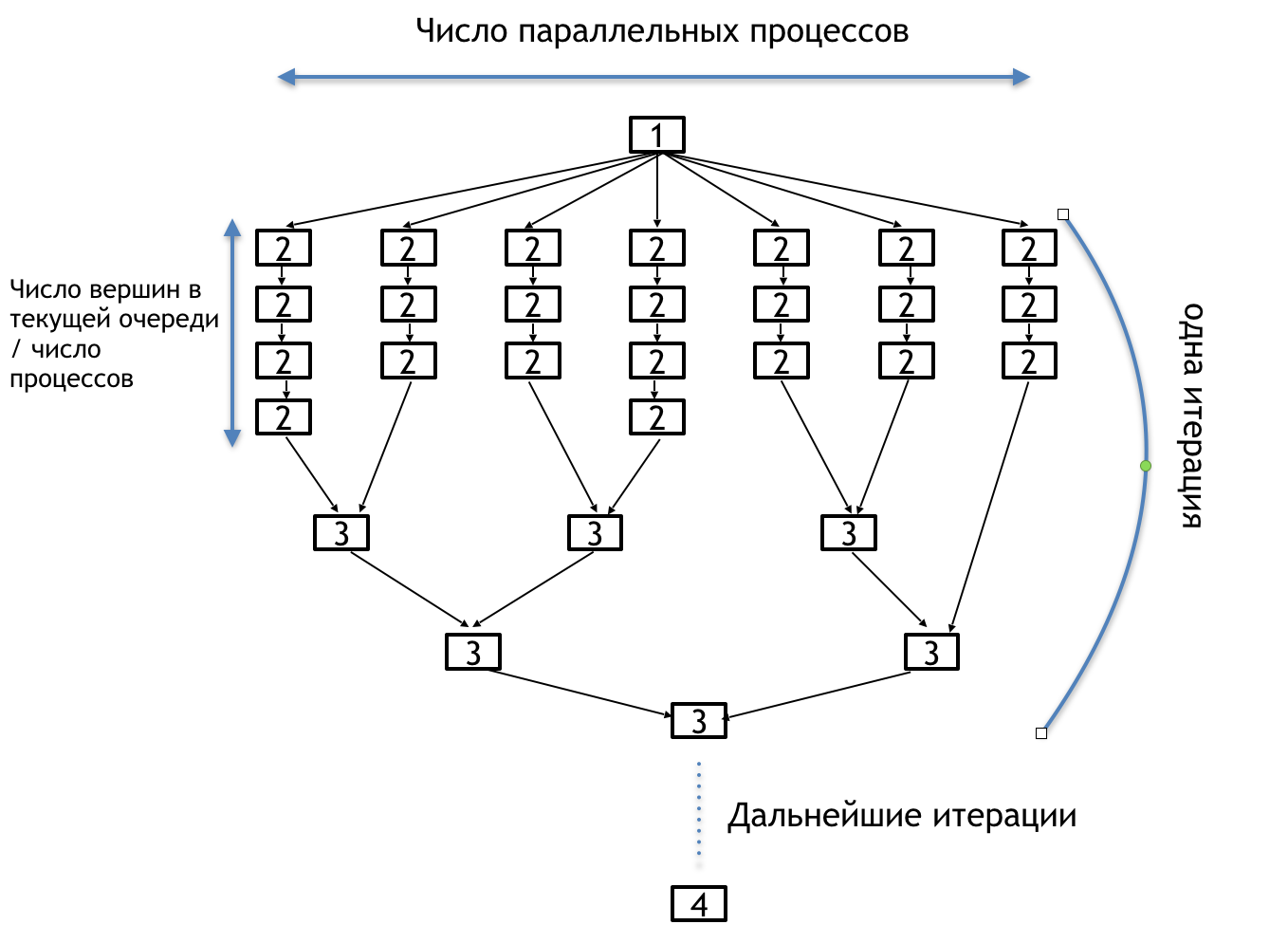
1.7 Информационный граф

Информационный граф

1.8 Ресурс параллелизма алгоритма

1.9 Входные и выходные данные алгоритма

1.10 Свойства алгоритма

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.2.1 Локальность реализации алгоритма

2.2.1.1 Структура обращений в память и качественная оценка локальности

2.2.1.2 Количественная оценка локальности

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

2.4.2 Масштабируемость реализации алгоритма

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Распределённый алгоритм поиска вширь является вычислительным ядром бенчмарка Graph500.
C++: Boost Graph Library (функции breadth_first_search, breadth_first_visit).
C++, MPI: Parallel Boost Graph Library (функция breadth_first_search).
Java: WebGraph (класс ParallelBreadthFirstVisit), многопоточная реализация.
Python: NetworkX (функция bfs_edges).
Python/C++: NetworKit (класс networkit.graph.BFS).

3 Литература

↑ Moore, Edward F. “The Shortest Path Through a Maze,” International Symposium on the Theory of Switching, 285–92, 1959.
↑ Lee, C Y. “An Algorithm for Path Connections and Its Applications.” IEEE Transactions on Electronic Computers 10, no. 3 (September 1961): 346–65. doi:10.1109/TEC.1961.5219222.

[1] Moore, Edward F. “The Shortest Path Through a Maze,” International Symposium on the Theory of Switching, 285–92, 1959.

[2] Lee, C Y. “An Algorithm for Path Connections and Its Applications.” IEEE Transactions on Electronic Computers 10, no. 3 (September 1961): 346–65. doi:10.1109/TEC.1961.5219222.

[1]

[2]

@@ Строка 10: / Строка 10: @@
 === Последовательная сложность алгоритма ===
 === Информационный граф ===
+Информационный граф
+[[Файл:BFS-информацинный_граф.png]]
 === Ресурс параллелизма алгоритма ===
 === Входные и выходные данные алгоритма ===