Приложение 4: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
[непроверенная версия][непроверенная версия]
(Полностью удалено содержимое страницы)
Строка 1: Строка 1:
 +
= Скалярное произведение векторов, вещественная версия, последовательно-параллельный вариант =
  
 +
== Свойства и структура алгоритма ==
 +
 +
=== Общее описание алгоритма ===
 +
 +
'''Скалярное произведение векторов''' используется в качестве одной из базовых операций в широком круге методов. При этом используется как в версии скалярного произведения собственно <math>n</math>-мерных векторов (одномерных массивов размера <math>n</math>), так и в версии скалярного произведения строк, столбцов и других линейных подмножеств массивов большей размерности. Последняя отличается от первой тем, что соответствующая подпрограмма получает, кроме стартовых адресов векторов, также и параметры смещения следующих элементов относительно предыдущих (в первой версии эти смещения равны 1). Разные формулы существуют для скалярных произведений в вещественной арифметике и для комплексных векторов. Здесь мы рассматриваем только вещественную арифметику и последовательно-параллельную реализацию.
 +
 +
=== Математическое описание алгоритма ===
 +
 +
Исходные данные: два одномерных массива n чисел.
 +
 +
Вычисляемые данные: сумма попарных произведений элементов массива.
 +
 +
Формулы метода:
 +
число <math>n</math> разлагается в выражение типа
 +
<math>n = (p - 1) k + q</math>,
 +
где <math>p</math> — количество процессоров, <math>k = \lceil \frac{n}{p} \rceil</math>,
 +
<math>q = n - k (p - 1)</math>.
 +
После этого на <math>i</math>-м процессоре (<math>i < p</math>) последовательно вычисляется «частичное» скалярное произведение подмассивов, начиная с <math>(i - 1) k + 1</math>-го номера элемента, до <math>ik</math>-го номера.
 +
 +
:<math>S_i = \sum_{j = 1}^k a_{k (i - 1) + j} b_{k (i - 1) + j}</math>
 +
 +
На <math>p</math>-м процессоре последовательно вычисляется «частичное» скалярное произведение подмассивов, начиная с <math>(p - 1) k + 1</math>-го номера элемента до <math>(p - 1) k + q</math>-го номера.
 +
 +
:<math>S_p = \sum_{j = 1}^q a_{k (p - 1) + j} b_{k (p - 1) + j}</math>
 +
 +
По окончании этого процесса процессоры обмениваются данными и на одном из них (либо на всех одновременно, если результат нужен далее на всех процессорах) получившиеся суммы суммируются последовательно друг с другом.
 +
 +
:<math>\sum_{i = 1}^p S_i</math>
 +
 +
При этом в последовательно-параллельном варианте при вычислений сумм из формул используется последовательный порядок суммирования (обычно от меньших индексов к большим).
 +
 +
=== Вычислительное ядро алгоритма ===
 +
 +
Вычислительное ядро скалярного произведения в последовательно-параллельном варианте можно представить как <math>p</math> вычислений «частных» скалярных произведений c последующим последовательным суммированием получившихся <math>p</math> чисел.
 +
 +
=== Макроструктура алгоритма ===
 +
 +
Как уже записано в описании ядра алгоритма, основную часть вычисления скалярного произведения составляют параллельное вычисление скалярных произведений меньшей размерности последовательным методом и последовательное вычисление суммы получившихся «частных» скалярных произведений подмассивов.
 +
 +
=== Схема реализации последовательного алгоритма ===
 +
 +
Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов).
 +
 +
=== Последовательная сложность алгоритма ===
 +
 +
Для вычисления скалярного произведения массивов, состоящих из <math>n</math> элементов, при любых разложениях количество операций умножения неизменно и равно <math>n</math>, а количество операций сложения равно <math>n - 1</math>. Поэтому алгоритм должен быть отнесён к алгоритмам ''линейной'' сложности по количеству последовательных операций.
 +
 +
=== Информационный граф ===
 +
 +
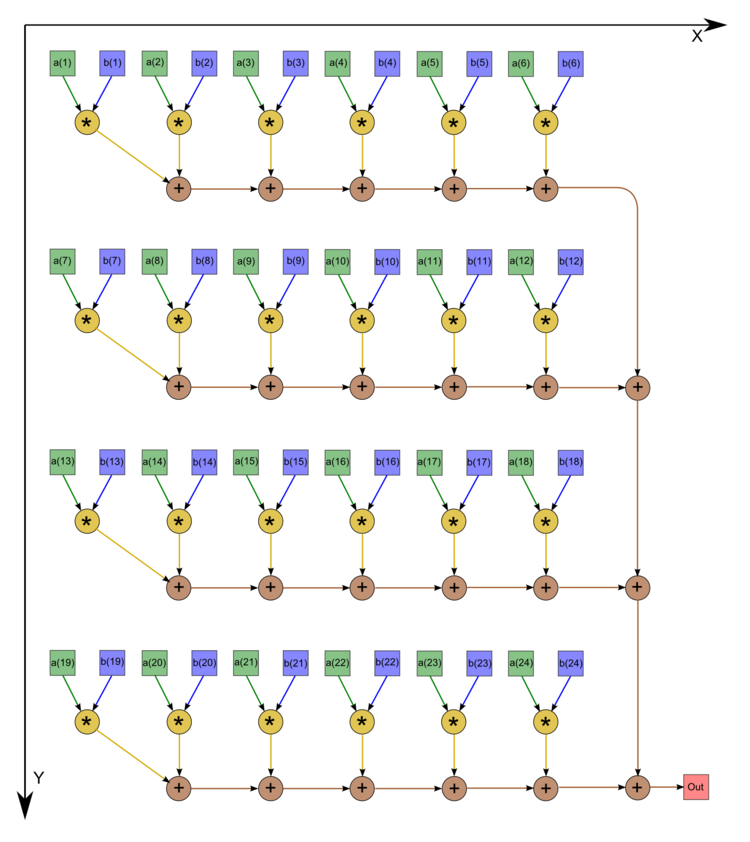
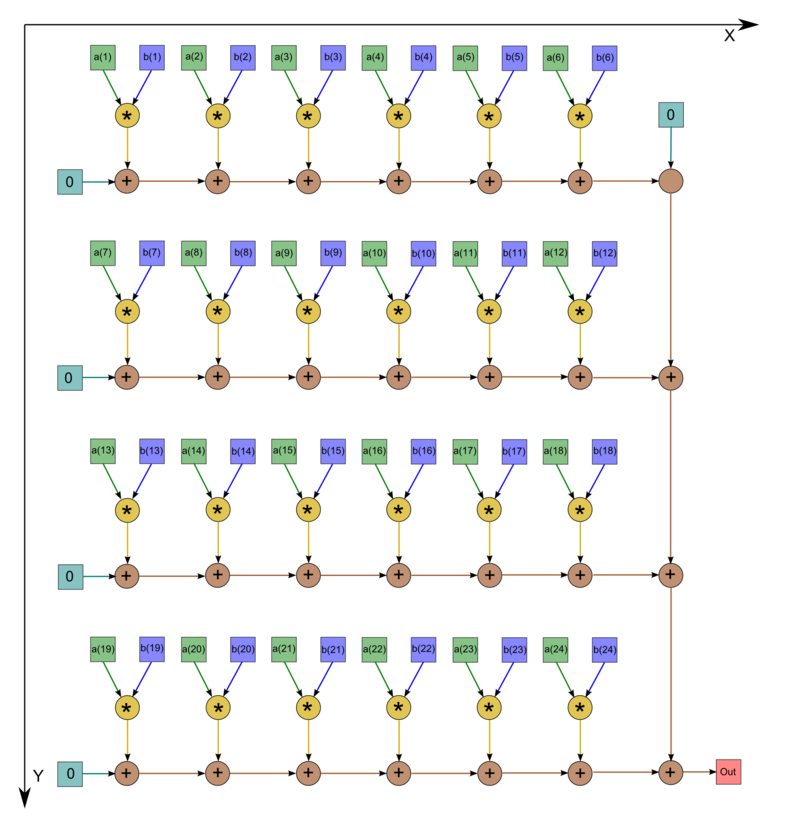
На рис.1 изображён граф аогоритма. Однако следует отметить, что в большинстве случаев программисты не экономят на одном вызове операции сложения, а инициализируют начальное значение переменной нулём. В этом случае граф становится таким, как на рис.2 (n=24).
 +
 +
{| align="left"
 +
    |- valign="top"
 +
    | [[file:series-parallel dot product graph.png|thumb|750px|Рисунок 1. Последовательно-параллельное вычисление скалярного произведения с экономией операций сложения]]
 +
    | [[file:Series-parallel dot product graph straight.png|thumb|790px|Рисунок 2. Последовательно-параллельное вычисление скалярного произведения без экономии операций сложения]]
 +
|}
 +
 +
=== Ресурс параллелизма алгоритма ===
 +
 +
Для вычисления скалярного произведения массивов порядка <math>n</math> последовательно-параллельным методом в параллельном варианте требуется последовательно выполнить следующие ярусы:
 +
* 1 ярус вычисления произведений,
 +
* <math>k - 1</math> ярусов суммирования по частям массивов (<math>p</math> ветвей),
 +
* <math>p - 1</math> ярусов суммирования (одна последовательная ветвь).
 +
 +
Таким образом, в параллельном варианте критический путь алгоритма  (и соответствующая ему высота ЯПФ) будет зависеть от произведённого разбиения массива на части. В оптимальном случае (<math>p = \sqrt{n}</math>) высота ЯПФ будет равна <math> 2 \sqrt{n} - 1</math>. При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам ''со сложностью «корень квадратный»''. При классификации по ширине ЯПФ его сложность также будет ''«корень квадратный»''.
 +
 +
=== Входные и выходные данные алгоритма ===
 +
 +
Входные данные: массивы <math>a</math> (элементы <math>a_i</math>), <math>b</math> (элементы <math>b_i</math>).
 +
 +
Дополнительные ограничения: отсутствуют.
 +
 +
Объём входных данных: <nowiki/><math>2 n</math>.
 +
 +
Выходные данные: сумма попарных произведений элементов массивов.
 +
 +
Объём выходных данных: один скаляр.
 +
 +
=== Свойства алгоритма ===
 +
 +
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является ''корнем квадратным'' (отношение линейной к корню квадратному). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего ''1 (входных и выходных данных почти столько же, сколько операций; если точнее - даже больше на 2)''. При этом алгоритм полностью детерминирован при заданном разложении <math>n</math>. Дуги информационного графа локальны. Для уменьшения ошибок округления режимом накопления в ряде алгоритмов, использующих скалярное произведение одинарной точности, оно вычисляется с двойной точностью. Впрочем, у последовательно-параллельного способа вычисления скалярного произведения и без режима накопления влияние ошибок округления «в среднем» меньше в <math>\sqrt{n}</math> раз.
 +
 +
== Литература ==
 +
<references />

Версия 11:10, 17 сентября 2015

1 Скалярное произведение векторов, вещественная версия, последовательно-параллельный вариант

1.1 Свойства и структура алгоритма

1.1.1 Общее описание алгоритма

Скалярное произведение векторов используется в качестве одной из базовых операций в широком круге методов. При этом используется как в версии скалярного произведения собственно [math]n[/math]-мерных векторов (одномерных массивов размера [math]n[/math]), так и в версии скалярного произведения строк, столбцов и других линейных подмножеств массивов большей размерности. Последняя отличается от первой тем, что соответствующая подпрограмма получает, кроме стартовых адресов векторов, также и параметры смещения следующих элементов относительно предыдущих (в первой версии эти смещения равны 1). Разные формулы существуют для скалярных произведений в вещественной арифметике и для комплексных векторов. Здесь мы рассматриваем только вещественную арифметику и последовательно-параллельную реализацию.

1.1.2 Математическое описание алгоритма

Исходные данные: два одномерных массива n чисел.

Вычисляемые данные: сумма попарных произведений элементов массива.

Формулы метода: число [math]n[/math] разлагается в выражение типа [math]n = (p - 1) k + q[/math], где [math]p[/math] — количество процессоров, [math]k = \lceil \frac{n}{p} \rceil[/math], [math]q = n - k (p - 1)[/math]. После этого на [math]i[/math]-м процессоре ([math]i \lt p[/math]) последовательно вычисляется «частичное» скалярное произведение подмассивов, начиная с [math](i - 1) k + 1[/math]-го номера элемента, до [math]ik[/math]-го номера.

[math]S_i = \sum_{j = 1}^k a_{k (i - 1) + j} b_{k (i - 1) + j}[/math]

На [math]p[/math]-м процессоре последовательно вычисляется «частичное» скалярное произведение подмассивов, начиная с [math](p - 1) k + 1[/math]-го номера элемента до [math](p - 1) k + q[/math]-го номера.

[math]S_p = \sum_{j = 1}^q a_{k (p - 1) + j} b_{k (p - 1) + j}[/math]

По окончании этого процесса процессоры обмениваются данными и на одном из них (либо на всех одновременно, если результат нужен далее на всех процессорах) получившиеся суммы суммируются последовательно друг с другом.

[math]\sum_{i = 1}^p S_i[/math]

При этом в последовательно-параллельном варианте при вычислений сумм из формул используется последовательный порядок суммирования (обычно от меньших индексов к большим).

1.1.3 Вычислительное ядро алгоритма

Вычислительное ядро скалярного произведения в последовательно-параллельном варианте можно представить как [math]p[/math] вычислений «частных» скалярных произведений c последующим последовательным суммированием получившихся [math]p[/math] чисел.

1.1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть вычисления скалярного произведения составляют параллельное вычисление скалярных произведений меньшей размерности последовательным методом и последовательное вычисление суммы получившихся «частных» скалярных произведений подмассивов.

1.1.5 Схема реализации последовательного алгоритма

Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов).

1.1.6 Последовательная сложность алгоритма

Для вычисления скалярного произведения массивов, состоящих из [math]n[/math] элементов, при любых разложениях количество операций умножения неизменно и равно [math]n[/math], а количество операций сложения равно [math]n - 1[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.

1.1.7 Информационный граф

На рис.1 изображён граф аогоритма. Однако следует отметить, что в большинстве случаев программисты не экономят на одном вызове операции сложения, а инициализируют начальное значение переменной нулём. В этом случае граф становится таким, как на рис.2 (n=24).

Рисунок 1. Последовательно-параллельное вычисление скалярного произведения с экономией операций сложения
Рисунок 2. Последовательно-параллельное вычисление скалярного произведения без экономии операций сложения

1.1.8 Ресурс параллелизма алгоритма

Для вычисления скалярного произведения массивов порядка [math]n[/math] последовательно-параллельным методом в параллельном варианте требуется последовательно выполнить следующие ярусы:

  • 1 ярус вычисления произведений,
  • [math]k - 1[/math] ярусов суммирования по частям массивов ([math]p[/math] ветвей),
  • [math]p - 1[/math] ярусов суммирования (одна последовательная ветвь).

Таким образом, в параллельном варианте критический путь алгоритма (и соответствующая ему высота ЯПФ) будет зависеть от произведённого разбиения массива на части. В оптимальном случае ([math]p = \sqrt{n}[/math]) высота ЯПФ будет равна [math] 2 \sqrt{n} - 1[/math]. При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам со сложностью «корень квадратный». При классификации по ширине ЯПФ его сложность также будет «корень квадратный».

1.1.9 Входные и выходные данные алгоритма

Входные данные: массивы [math]a[/math] (элементы [math]a_i[/math]), [math]b[/math] (элементы [math]b_i[/math]).

Дополнительные ограничения: отсутствуют.

Объём входных данных: [math]2 n[/math].

Выходные данные: сумма попарных произведений элементов массивов.

Объём выходных данных: один скаляр.

1.1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является корнем квадратным (отношение линейной к корню квадратному). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных почти столько же, сколько операций; если точнее - даже больше на 2). При этом алгоритм полностью детерминирован при заданном разложении [math]n[/math]. Дуги информационного графа локальны. Для уменьшения ошибок округления режимом накопления в ряде алгоритмов, использующих скалярное произведение одинарной точности, оно вычисляется с двойной точностью. Впрочем, у последовательно-параллельного способа вычисления скалярного произведения и без режима накопления влияние ошибок округления «в среднем» меньше в [math]\sqrt{n}[/math] раз.

1.2 Литература

Источник — https://algowiki-project.org/w/ru/index.php?title=Приложение_4&oldid=2541