Участник:Даниил Глазков/Алгоритм кластеризации DBSCAN: различия между версиями
| Строка 70: | Строка 70: | ||
1. Разделение данных | 1. Разделение данных | ||
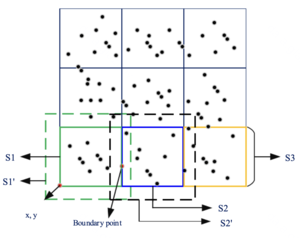
| − | Набор данных <math> D </math> разбивается на несколько непересекающихся подмножеств <math> D_1, D_2, \ldots, D_k </math>. При этом каждая часть данных обрабатывается независимо, что позволяет эффективно распределить вычисления между узлами параллельной | + | Набор данных <math> D </math> разбивается на несколько непересекающихся подмножеств <math> D_1, D_2, \ldots, D_k </math>. При этом каждая часть данных обрабатывается независимо, что позволяет эффективно распределить вычисления между узлами параллельной |
| + | |||
| + | [[Файл:Разбиение данных.png|мини]] | ||
2. Локальное выполнение DBSCAN | 2. Локальное выполнение DBSCAN | ||
Версия 21:36, 6 декабря 2024
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм DBSCAN (Density-Based Spatial Clustering of Applications with Noise) — это алгоритм кластеризации, предназначенный для решения задачи обнаружения плотных областей в пространстве данных и выделения их как кластеров. Этот алгоритм относится к классу алгоритмов плотностной кластеризации, где основным критерием для объединения точек в кластеры является их плотность.
В отличие от алгоритмов, основанных на минимизации расстояний между точками (например, K-средних), DBSCAN автоматически определяет количество кластеров и не требует задания их количества заранее. Кроме того, DBSCAN хорошо справляется с шумами и выбросами, поскольку точки, не принадлежащие к плотным областям, маркируются как шумовые.
Особенности объектов, с которыми работает DBSCAN:
- Входные данные представлены набором точек в пространстве, где каждая точка характеризуется набором признаков. Для двухмерного пространства точки могут быть представлены как (x, y), но алгоритм также применим и для данных с большим числом признаков.
- Алгоритм подходит для плотностных структур, где кластеры имеют разную форму и размеры, что делает его особенно полезным для географических и пространственных данных.
Основные параметры DBSCAN:
- eps — радиус, в пределах которого точки считаются соседними и могут быть включены в один кластер.
- minPts — минимальное количество точек, необходимых для того, чтобы область считалась "плотной" и могла образовать кластер.
Алгоритм выделяет три типа точек:
1. Ядровые точки: точки, которые имеют по меньшей мере minPts соседей в радиусе eps. Эти точки образуют ядро кластера.
2. Граничные точки: точки, которые находятся в радиусе eps от ядровой точки, но сами не обладают достаточным количеством соседей, чтобы быть ядровыми.
3. Шумовые точки: точки, которые не принадлежат ни к одному кластеру, так как не попадают в плотные области.
DBSCAN широко применяется в задачах с нерегулярной структурой данных и особенно полезен в задачах обработки пространственных данных и аномалий.
1.2 Математическое описание алгоритма
Пусть имеется множество точек [math] \mathcal{D} = \{p_1, p_2, \dots, p_n\} [/math] в d-мерном пространстве, где каждая точка [math] p_i \in \mathbb{R}^d [/math] характеризуется d признаками. Определим формально параметры:
1. Радиус eps > 0.
2. Параметр плотности [math] minPts \in \mathbb{N} [/math], указывающий минимальное количество точек, необходимых для формирования кластера.
Для каждой точки [math] p_i \in \mathcal{D} [/math], определим её eps-окрестность:
[math]N_{\varepsilon}(p_i) = \{p_j \in \mathcal{D} \mid d(p_i, p_j) \leq \varepsilon\}[/math]
где [math] d(p_i, p_j) [/math] — метрика расстояния, например, Евклидово расстояние.
Для определения точек в терминах DBSCAN вводятся следующие условия:
- Ядровая точка: точка [math] p_i [/math] считается ядровой, если [math] |N_{\varepsilon}(p_i)| \geq minPts [/math].
- Граничная точка: точка [math] p_j [/math] считается граничной, если [math] p_j [/math] находится в \eps-окрестности ядровой точки, но сама не является ядровой.
- Шумовая точка: точка <marh> p_k </math> не является ни ядровой, ни граничной, если [math] |N_{\varepsilon}(p_k)| \lt minPts [/math] и она не принадлежит eps-окрестности ни одной из ядровых точек.
Процесс кластеризации:
1. Для каждой точки [math] p_i \in \mathcal{D} [/math]:
- Если [math] p_i [/math] является ядровой точкой, то создаётся новый кластер C.
- Все точки в eps-окрестности [math] p_i [/math] добавляются в кластер C.
- Процесс расширения продолжается рекурсивно для всех ядровых точек в окрестности.
2. Граничные точки добавляются в кластеры, если они находятся в окрестности eps хотя бы одной ядровой точки, но не создают новые кластеры.
3. Все оставшиеся точки, не принадлежащие ни одному кластеру, считаются шумовыми.
Таким образом, DBSCAN создает множество кластеров [math] \{C_1, C_2, \dots, C_k\} [/math], где k — количество обнаруженных кластеров, а точки, не входящие ни в один из [math] C_i [/math], классифицируются как шумовые точки.
1.3 Вычислительное ядро алгоритма
Основные этапы ядра алгоритма:
1. Разделение данных Набор данных [math] D [/math] разбивается на несколько непересекающихся подмножеств [math] D_1, D_2, \ldots, D_k [/math]. При этом каждая часть данных обрабатывается независимо, что позволяет эффективно распределить вычисления между узлами параллельной
2. Локальное выполнение DBSCAN На каждом подмножестве [math] D_i [/math] выполняется локальная версия алгоритма DBSCAN:
- Поиск [math] \varepsilon [/math]-соседей для каждой точки в [math] D_i [/math].
- Проверка, является ли точка плотностным ядром в рамках текущего подмножества [math] D_i [/math].
- Формирование локальных кластеров.
Эти операции аналогичны стандартному алгоритму DBSCAN, но выполняются только на локальных подмножествах, что снижает вычислительную сложность в каждом
3. Слияние границ кластеров. После обработки всех подмножеств необходимо объединить кластеры, пересекающие границы [math] D_i [/math] и [math] D_j [/math]. Это достигается путём:
- Если граничная точка [math] P \in D_i [/math] имеет соседей в [math] D_j [/math], то выполняется пересечения кластеров
1.4 Макроструктура алгоритма
- Разбиение данных на подмножества: На этом этапе набор данных [math]D[/math] разбивается на несколько непересекающихся подмножеств [math]D_1, D_2, \ldots, D_k[/math]
- Кластеризация: Основной этап алгоритма. Для каждого полученного подмножества применяется алгоритм кластеризации DBSCAN
- Слияние кластеров на границах: Если точка [math] P \in D_i [/math] имеет соседей в [math] D_j [/math], то выполняется пересечения кластеров
1.5 Схема реализации последовательного алгоритма
Псевдокод для реализации алгоритма DBSCAN
# Инициализация
clusters = []
visited = set()
noise = set()
# Основная итерация
for P in dataset:
if P in visited:
continue
visited.add(P)
# Поиск соседей
neighbors = find_neighbors(P, epsilon)
if len(neighbors) < MinPts:
noise.add(P)
continue
# Создание нового кластера
cluster = []
clusters.append(cluster)
cluster.append(P)
# Расширение кластера
expand_cluster(P, neighbors, cluster, visited, epsilon, MinPts)
# Возврат результатов
return clusters, noise
1.6 Последовательная сложность алгоритма
Разбиение данных на подмножества:
- Функция для разбиения имеет временную сложность O(N), так как она проходит по всем точкам и проверяет их принадлежность к региону.
Кластеризация точек:
- Основная часть алгоритма — это функция кластеризация DBSCAN, которая выполняет поиск соседних точек и расширение кластера. В худшем случае, алгоритм может обрабатывать все точки, что приводит к временной сложности [math]O(N^2)[/math] для одного процесса. Поскольку алгоритм параллельный и точки распределены между процессами, временная сложность для каждого процесса будет [math]O((N/P)^2)[/math], где P — количество процессов.
Объединение пересекающихся кластеров:
- Функция объединения кластеров имеет временную сложность [math]O(N^2)[/math], так как она проходит по всем точкам и проверяет совпадение координат для граничных точек.
Общая временная сложность алгоритма для одного процесса составляет [math]O(N^2)[/math]. В параллельной версии с P процессами временная сложность для каждого процесса составляет [math]O((N/P)^2)[/math]. Однако, учитывая накладные расходы на коммуникацию между процессами, общая временная сложность параллельного алгоритма будет примерно [math]O(N^2/P)[/math].
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
2 Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
2.2 Существующие реализации алгоритма
3 Литература
1. Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, № 7, С. 36-39.
2. https://www.sciencedirect.com/science/article/pii/S0165178123002159#sec0002