Нахождение суммы элементов массива сдваиванием: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
VadimVV (обсуждение | вклад) |
VadimVV (обсуждение | вклад) |
||
| Строка 67: | Строка 67: | ||
На рис. 12.1 представлен профиль обращений в память для реализации суммирования элементов массива методом сдваивания. Данный профиль устроен достаточно просто – он представляет собой набор итераций, на каждой итерации происходит последовательный перебор элементов массива с некоторым шагом, причем с каждой следующей итерацией шаг увеличивается вдвое. Этим обуславливается тот факт, что на рис. 12.1 каждая следующая прямая расположена под большим углом. Подобный профиль обладает достаточно высокой пространственной локальностью, поскольку большая часть обращений происходит к соседним или близким элементам. Однако при этом временная локальность низка – к половине элементов обращения происходят только однажды, к четверти – дважды и т.д. | На рис. 12.1 представлен профиль обращений в память для реализации суммирования элементов массива методом сдваивания. Данный профиль устроен достаточно просто – он представляет собой набор итераций, на каждой итерации происходит последовательный перебор элементов массива с некоторым шагом, причем с каждой следующей итерацией шаг увеличивается вдвое. Этим обуславливается тот факт, что на рис. 12.1 каждая следующая прямая расположена под большим углом. Подобный профиль обладает достаточно высокой пространственной локальностью, поскольку большая часть обращений происходит к соседним или близким элементам. Однако при этом временная локальность низка – к половине элементов обращения происходят только однажды, к четверти – дважды и т.д. | ||
| + | |||
| + | ===== Количественная оценка локальности ===== | ||
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg. | Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg. | ||
| Строка 80: | Строка 82: | ||
[[file:Sum doub cvg.png|thumb|center|700px|Рисунок 12.2. Сравнение значений оценки cvg]] | [[file:Sum doub cvg.png|thumb|center|700px|Рисунок 12.2. Сравнение значений оценки cvg]] | ||
| − | |||
===== Анализ на основе теста Apex-Map ===== | ===== Анализ на основе теста Apex-Map ===== | ||
Версия 16:30, 17 сентября 2014
Содержание
- 1 Описание свойств и структуры алгоритма
- 1.1 Словесное описание алгоритма
- 1.2 Математическое описание
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Описание схемы реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Описание входных и выходных данных
- 1.10 Свойства алгоритма
- 2 Программная реализация
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Описание локальности данных и вычислений
- 2.3 Возможные способы и особенности реализации параллельного алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
1 Описание свойств и структуры алгоритма
1.1 Словесное описание алгоритма
Метод сдваивания используется в качестве быстрого варианта вычисления длинных последовательностей ассоциативных операций (например, массового суммирования). Получил распространение благодаря как наименьшей из возможных высоте алгортима, так и из-за ряда своих вычислительных характеристик, а также (в среде нечисленных алгоритмов) из-за своей рекурсивности, то есть лёгкости записи.
1.2 Математическое описание
Исходные данные: одномерный массив [math]n[/math] чисел.
Вычисляемые данные: сумма элементов массива.
Формулы метода: элементы на каждом этапе алгоритма разбиваются на пары. В каждой из пар находится сумма составляющих её элементов. На следующем этапе на пары разбиваются уже эти суммы (и те элементы, которые не вошли в уже вычисленные суммы), и т. д.
1.3 Вычислительное ядро алгоритма
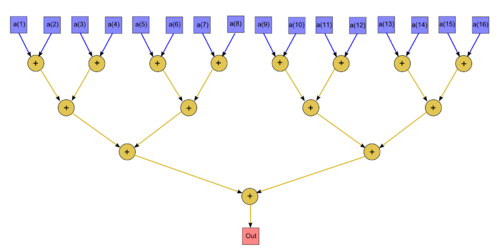
Вычислительное ядро последовательно-параллельного метода суммирования можно составить как из элементарных бинарных (всего [math]n - 1[/math]) вычислений сумм, так и (рекуррентно) из набора реализаций метода сдваивания меньших размерностей.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть метода составляют рекурсивные вызовы сумм массивов меньшей размерности.
1.5 Описание схемы реализации последовательного алгоритма
В своём чистом виде суммирование сдваиванием редко используют при последовательной реализации, поскольку при этом усложняется общая схема алгоритма и резко растёт потребность в памяти, нужной для хранения промежуточных данных.
1.6 Последовательная сложность алгоритма
Для вычисления суммы массива, состоящего из [math]N[/math] элементов, при любых разложениях [math]N[/math] на пары суть алгоритма сводится к простому переставлению скобок в формуле суммирования, и количество операций неизменно и равно [math]N - 1[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.
1.7 Информационный граф
Опишем граф алгоритма в виде рисунка. В данном случае выполнено суммирование 16 элементов массива.
1.8 Описание ресурса параллелизма алгоритма
Для суммирования массива порядка [math]n[/math] методом сдваивания в параллельном варианте требуется последовательно выполнить [math]\lceil \log_2 n \rceil[/math] ярусов с убывающим (от [math]\frac{n}{2}[/math] до [math]1[/math]) количеством операций суммирования. При классификации по высоте ЯПФ, таким образом, метод сдваивания относится к алгоритмам с логарифмической сложностью. При классификации по ширине ЯПФ его сложность будет линейной.
1.9 Описание входных и выходных данных
Входные данные: массив [math]x[/math] (элементы [math]x_i[/math]).
Дополнительные ограничения: отсутствуют.
Объём входных данных: [math]N[/math].
Выходные данные: сумма элементов массива.
Объём выходных данных: один скаляр.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является [math]\frac{n}{\log_2 n}[/math] (отношение линейной к логарифмической). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных столько же, сколько операций). При этом алгоритм полностью детерминирован. Дуги информационного графа нелокальны, от яруса к ярусу наблюдается показательный рост их длины, при любом размещении вершин графа.
2 Программная реализация
2.1 Особенности реализации последовательного алгоритма
2.2 Описание локальности данных и вычислений
2.2.1 Описание локальности алгоритма
2.2.2 Описание локальности реализации алгоритма
2.2.2.1 Описание структуры обращений в память и качественная оценка локальности
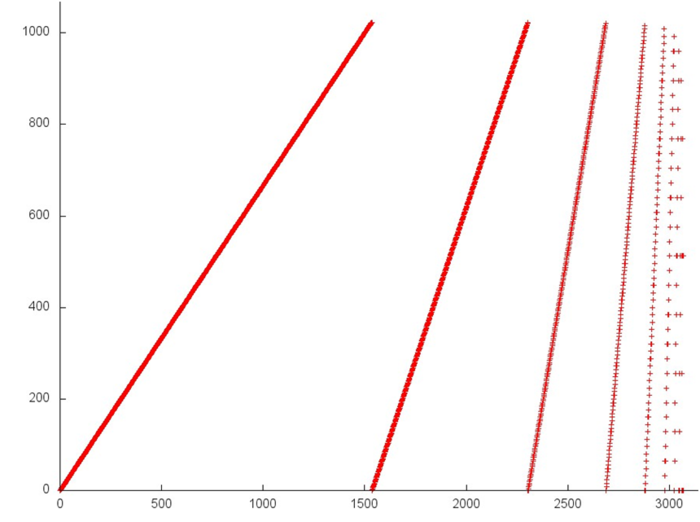
На рис. 12.1 представлен профиль обращений в память для реализации суммирования элементов массива методом сдваивания. Данный профиль устроен достаточно просто – он представляет собой набор итераций, на каждой итерации происходит последовательный перебор элементов массива с некоторым шагом, причем с каждой следующей итерацией шаг увеличивается вдвое. Этим обуславливается тот факт, что на рис. 12.1 каждая следующая прямая расположена под большим углом. Подобный профиль обладает достаточно высокой пространственной локальностью, поскольку большая часть обращений происходит к соседним или близким элементам. Однако при этом временная локальность низка – к половине элементов обращения происходят только однажды, к четверти – дважды и т.д.
2.2.2.2 Количественная оценка локальности
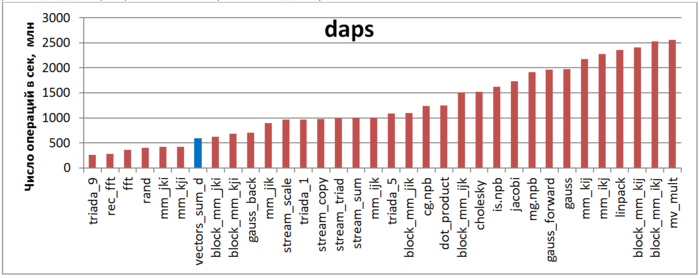
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рисунке 12.2 значения приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что из-за низкой временной локальности значение daps для данной программы находится на уровне самых неэффективных вариантов реализации перемножения матриц и лишь немногим лучше реализации программы со случайным доступом.
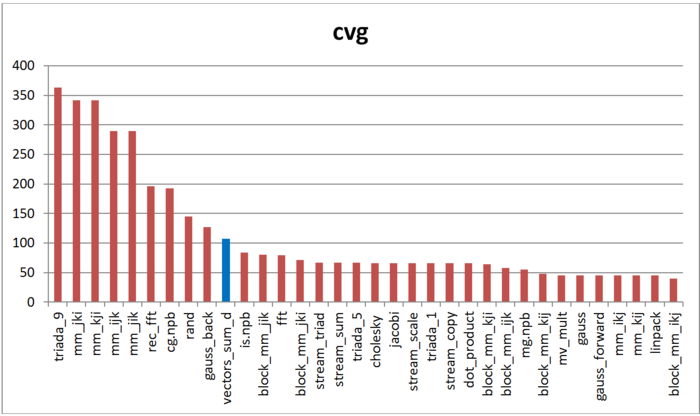
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рисунке 12.3 значения приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, локальность реализации суммирования сдваиванием достаточно низка, что согласуется с результатами по оценке daps и анализом самого профиля обращений.