Участница:Sannikovats/Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки (1): различия между версиями
(Новая страница: «{{algorithm | name = Вычисление определённого интеграла с использованием адаптивно сгуща…») |
|||
| Строка 8: | Строка 8: | ||
}} | }} | ||
| − | Основные авторы описания:[[Участница:Sannikovats| Санникова Татьяна Сергеевна]],[[Участник:Plukshin| Лукшин | + | Основные авторы описания:[[Участница:Sannikovats| Санникова Татьяна Сергеевна]],[[Участник:Plukshin| Лукшин Петр Андреевич]]. |
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
Версия 23:50, 11 октября 2016
| Вычисление определённого интеграла с использованием адаптивно сгущающейся сетки | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]...[/math] |
| Объём входных данных | [math]...[/math] |
| Объём выходных данных | [math]...[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]...[/math] |
| Ширина ярусно-параллельной формы | [math]...[/math] |
Основные авторы описания: Санникова Татьяна Сергеевна, Лукшин Петр Андреевич.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
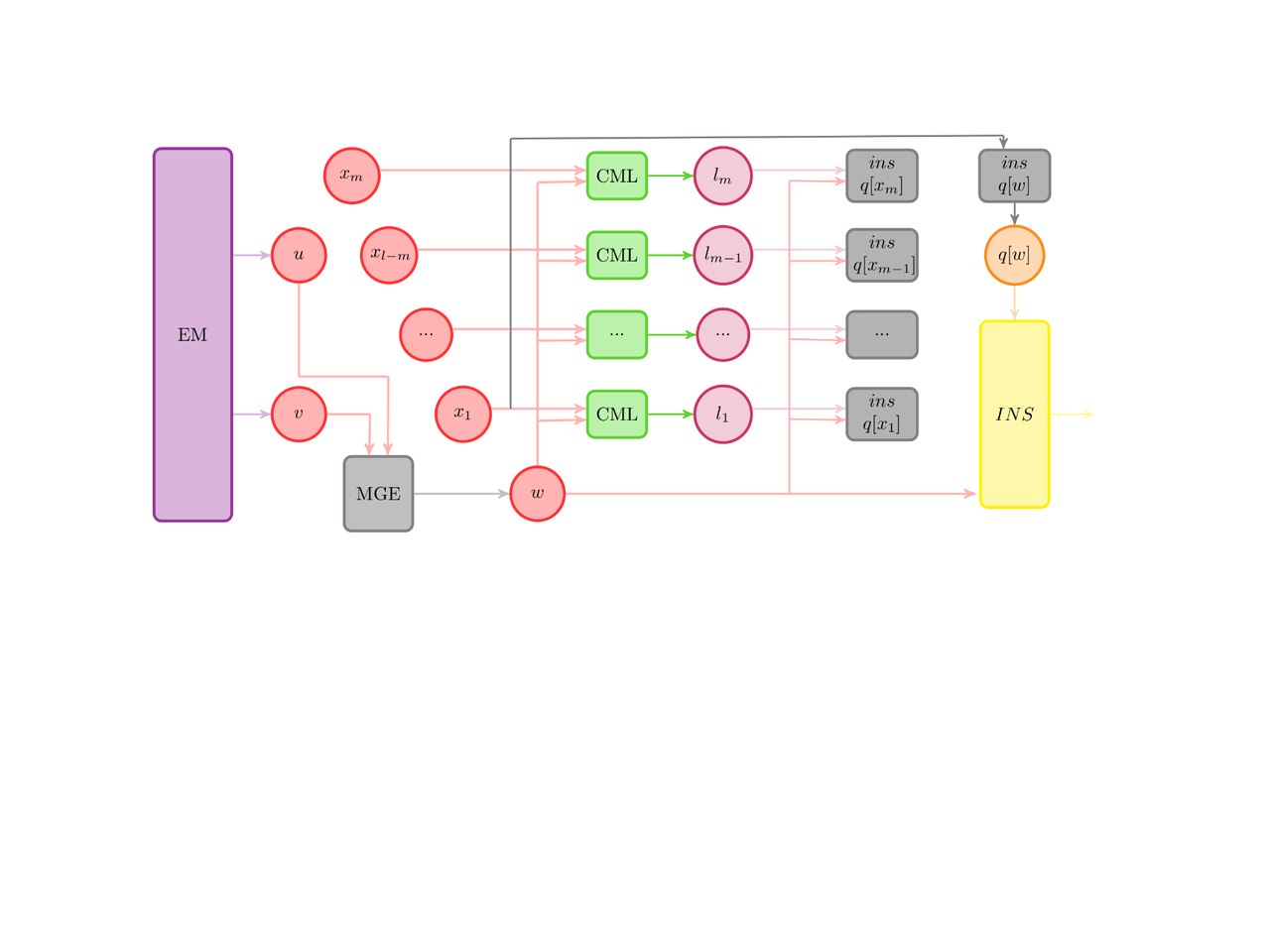
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Допустим, нам дана функция [math]f(x)[/math] , определенная на отрезке, и возможность получать ее численное значение в любой из точек области определения за фиксированное время. Задача — вычислить определенный интеграл данной функции по заданной области и дать оценку погрешности вычисления.
Существуют различные методы построения адаптивных подвижных сеток, которые позволяют значительно повысить точность вычисления определенного интеграла за счет учета характера изменения подынтегральной функции. В данной статье будет рассмотрен простейший метод рекурсивного деления, выигрыш от применения которого достигается за счет возможности использования сеток с разным числом узлов на разных участках интервала интегрирования.
Суть метода: интервал интегрирования разбивается на две части и независимо интегрируется функция [math]f(x)[/math] на каждой из них при соответствующих шагах интегрирования. Процедуру разбиения отрезков можно рекурсивно повторить до получения отрезков, на которых подынтегральная функция имеет простой вид и может быть аппроксимирована отрезком прямой с заданной точностью.
1.2 Математическое описание алгоритма
"Исходные данные:" заданная функция [math]f(x)[/math], определенная на отрезке [math][A,B][/math],точное решение, заданная точность решения ε.
"Выходные данные:" число, представляющее собой приближенное значение интеграла.
В качестве модельной задачи рассматривается проблема вычисления с точностью ε значения определенного интеграла