Участник:Bagnikita/Face Recognition: различия между версиями
Bagnikita (обсуждение | вклад) |
Bagnikita (обсуждение | вклад) |
||
| Строка 56: | Строка 56: | ||
После выполнения поиска в базе необходимо произвести нормализацию полученных значений оценивающей функции. В системах распознавания лиц обычно используют диапазон [0.0 - 1.0], где 0.0 означает минимальное сходство двух изображений лиц, а 1.0 максимальное. | После выполнения поиска в базе необходимо произвести нормализацию полученных значений оценивающей функции. В системах распознавания лиц обычно используют диапазон [0.0 - 1.0], где 0.0 означает минимальное сходство двух изображений лиц, а 1.0 максимальное. | ||
| + | |||
| + | === Вычислительное ядро алгоритма === | ||
| + | |||
| + | Основные операции составляют построение биометрического шаблона, и поиск в базе | ||
| + | |||
| + | ==== Построение биометрического шаблона ==== | ||
| + | |||
| + | Обозначим за <math>E(w,h,c)</math> сложность операции вычисления биометричсекого шаблона по входному изображению лица человека. Поскольку сверточной нейронной сети с полносвязными слоями должно подаваться на вход изображения фиксированного размера, то необходимо изменить разрешение исходного изображения. В данной реализации алгоритма распознавания лиц используется билинейная интерполяция. Нейронная сеть получает на вход одноканальные изображения размером <math>100*100</math>. Поэтому число необходимых операций (по операциям умножения) можно оценить как <math>O(w*h*c) + O(100 * 100 * 6) = O(w*h*c) + Const</math>. На практике эта константа существенна, поскольку эти операции неоднородны по памяти. | ||
| + | |||
| + | Непосредственно время работы нейронной сети существенно зависит от предложенной архитектуры (глубины сети, типов слоев и числа выходов каждого слоя). | ||
| + | |||
| + | В реализации, предлолженной в практической части, используются более 10 сверточных слоев. Количестве операций можно оценить исходя из количества весов связей в нейронной сети - 80M и размера сверток <math>3*3</math>. Оценка числа операций получилась ~2 GFlops на одну операцию применения нейросети (forward pass, 180ms). Она согласуется с реальным временем работы системы и производительностью системы на тесте linpack (130GFlops 4 cores) на ноутбуке. | ||
| + | |||
| + | ==== Поиск в базе ==== | ||
| + | |||
| + | Поиск в базе состоит из следующих частей: | ||
| + | * сравнение между собой двух дескрипторов изображений и вычисление метрики по базе | ||
| + | * агрегация результатов по людям | ||
| + | * сортировка по убыванию метрики сходства двух изображений | ||
| + | |||
| + | ===== Сравнение между собой двух дескрипторов изображений и вычисление метрики по базе ===== | ||
| + | |||
| + | В практической реализации алгоритма используется косинусовая метрика <math>M(x,y)=\frac{dot(x,y)}{\lVert x \lVert * \lVert y \lVert}</math>. Заметим, что вектора <math>x, y</math> уже нормированы на предыдущем этапе. Поэтому число операций для вычисления метрики составляет <math>d</math> умножений и <math>d - 1</math> сложений, где d - размерность дескриптора. В практической реализации размерность дескриптора 128. Если размер базы <math>n</math>, то число операций <math>O(n*d+n*(d-1))=O(n*d)</math>. | ||
| + | |||
| + | ===== Агрегация результатов по людям ===== | ||
| + | |||
| + | Для выполнения операции unique (без использования дополнительной памяти) необходимо отсортировать элементы (person_id, match_score) массива по ключу person_id, а при совпадении по score. После этого можно за линейное время удалить дубликаты по person_id, оставив первый элемент (который будет максимальным по match_score). Сложность таких операций <math>O(n*logn+n)=O(n*logn)</math>. | ||
| + | |||
| + | ===== Cортировка по убыванию метрики сходства двух изображений ===== | ||
| + | |||
| + | Финальная сортировка по match_score будет выполнена за O(n*logk), где k - количество результатов в выдаче. Обычно на практике число k не более 1000, поскольку обработка результата чаще всего производится вручную оператором. | ||
== Практическая реализация системы == | == Практическая реализация системы == | ||
Версия 14:24, 14 октября 2016
| Распознавание лиц | |
| Последовательный алгоритм | |
| Последовательная сложность | O(n*d) + O(n*log(n)) + O(E(w,h,c)) |
| Объём входных данных | w*h*c |
| Объём выходных данных | O(k) |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(k) |
| Ширина ярусно-параллельной формы | O(n) |
Основные авторы описания: Н.Ю.Багров
Содержание
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Распознавание лиц при помощи компьютера было впервые предложено в 1966 г. Woody Bledsoe и др. В первой системе использовался графический планшет, на котором было необходимо вручную отметить ключевые особенности на лице (брови, губы и тд). Система в дальнешейм использовала расстояния между этими точками для сравнения разных изображений. Поскольку требовалось много ручной работы, то оператор мог обработать около 40 изображений в час. В 1997 была создана система, которая непосредственно работала с видеоданными и могла применяться на практике. В дальшейшем с увеличением производительности вычислительных систем появились более качественные алгоритмы, но они заметно уступали человеку на данной задаче. С появлением высокороизводительных видеокарт в 2014 году появились системы, точность которых уже превышала точность оператора (человека). Основное преимущество таких систем в том, что они могут обрабатывать большие объемы данных - производительность человека намного ниже (требуется несколько секунд на сравнение пары изображений).
Задачу распознавания лиц можно разбить на несколько этапов:
- Обучение нейронной сети
- построение биометрического шаблона
- сравнение биометрических шаблонов
- поиск в базе и формирование результата
1.2 Математическое описание алгоритма
Алгоритм состоит из построения биометрических шаблонов (дескрипторов) по изображению и поиску заданного шаблона в базе уже вычисленных дескрипторов.
В дальшейшем будем рассматривать только сверточные нейронные сети. Классические архитектуры нейронных сетей с полносвязными слоями неприменимы на практике для анализа изображений, поскольку количество параметров такой сети экспоненциально возрастает с размером входных данных и количеством слоев. В таких сетях каждый нейрон не связан со всеми нейронами предыдущего слоя, а домножается на некоторый коэффициент (ядро свертки) по всему изображению. Таким образом, каждый такой слой применяет операцию свертки ко входам со своими коэффициентами, что заметно уменьшает число весов в нейронной сети. Это позволяет уменьшить потребление памяти и эффект переобучения сети, который проявляется в том, что сеть хорошо работает на классификации элементов обучающей выборки и хуже на валидационной.
1.2.1 Обучение сверточной нейронной сети
Для обучения нейронной сети используется стохастический градиентный спуск. Начальные веса сети устанавливаются случайными. Заметим, что существенное время занимают сверточные и полносвязные слои. Их можно свести к операции перемножения матриц следуюим образом:
- пусть размерность фильтра свертки k*k
- скопируем блоки исходного изображения размером k*k в столбцы новой матрицы
- умножим эту матрицу на коэффициеты фильтра свертки
- полученная матрица будет результатом применения свертки к входному изображению
Сложность задачи вычисления свертки зависит квадратично от размера фильтра и линейно от количества выходных данных.
FeatureMap = A^{n, w * h} * B^{w * h, c * k^2}, где FeatureMap - результат применения свертки, а A и B - входное изображение и матрица весов слоя нейронной сети
Существуют библиотеки (NVIDIA cuDNN) которые решают данную задачу более эффективно. Например, свертки размером 3x3, 5x5 могут быть реализованы с использованием FFT (что работает на видеокарте быстрее, чем умножение матриц)
1.2.2 Построение биометрического шаблона
Будем называть биометрическим шаблоном вектор {R}^d, который является представлением лица человека. Этот вектор получается после применения нейронной сети к изображению - в качестве такого вектора используют отклики с одного последних слоев нейронной сети. Для обеспечения возможности сравнивать между собой эти шаблоны вектор нормализуют.
1.2.3 Сравнение биометрических шаблонов
На предыдущем этапе был получен вектор значений D={A}^d, где d - размерность дескриптора. Можно рассматривать достаточно много различных оценивающих функций (метриками их называть некорректно, т.к для них не всегда выполняется неравенство треугольника). Например, в качестве такой функции можно рассматривать cosine distance - косинус угла между векторами-признаками в d-мерном пространстве. Также достаточно часто используют L2 метрику, либо более сложные контрукции, такие как Joint Bayesian. У всех таких "метрик" есть преимущества и недостатки, например в L2 можно легко проводить кластеризацию, тогда как в JointBayes и cosine metric нет. JointBayes можно дообучить на целевой выборке и повысить точность работы алгоритма.
1.2.4 Поиск в базе и формирование результата
Предположим, что для каждого человека в базе есть несколько фотографий. Тогда после выполнения операции сравнения биометрических шаблона изображения-запроса P и всех изображений в базе G={g1,g2,...,gn} необходимо выбрать результат с максимальным значением оценивающей функции для данного человека. Т.е необходимо оставить в результате только уникальные по людям совпадения, выбрав при этом максимальное значение при удалении дубликатов по людям.
После выполнения поиска в базе необходимо произвести нормализацию полученных значений оценивающей функции. В системах распознавания лиц обычно используют диапазон [0.0 - 1.0], где 0.0 означает минимальное сходство двух изображений лиц, а 1.0 максимальное.
1.3 Вычислительное ядро алгоритма
Основные операции составляют построение биометрического шаблона, и поиск в базе
1.3.1 Построение биометрического шаблона
Обозначим за E(w,h,c) сложность операции вычисления биометричсекого шаблона по входному изображению лица человека. Поскольку сверточной нейронной сети с полносвязными слоями должно подаваться на вход изображения фиксированного размера, то необходимо изменить разрешение исходного изображения. В данной реализации алгоритма распознавания лиц используется билинейная интерполяция. Нейронная сеть получает на вход одноканальные изображения размером 100*100. Поэтому число необходимых операций (по операциям умножения) можно оценить как O(w*h*c) + O(100 * 100 * 6) = O(w*h*c) + Const. На практике эта константа существенна, поскольку эти операции неоднородны по памяти.
Непосредственно время работы нейронной сети существенно зависит от предложенной архитектуры (глубины сети, типов слоев и числа выходов каждого слоя).
В реализации, предлолженной в практической части, используются более 10 сверточных слоев. Количестве операций можно оценить исходя из количества весов связей в нейронной сети - 80M и размера сверток 3*3. Оценка числа операций получилась ~2 GFlops на одну операцию применения нейросети (forward pass, 180ms). Она согласуется с реальным временем работы системы и производительностью системы на тесте linpack (130GFlops 4 cores) на ноутбуке.
1.3.2 Поиск в базе
Поиск в базе состоит из следующих частей:
- сравнение между собой двух дескрипторов изображений и вычисление метрики по базе
- агрегация результатов по людям
- сортировка по убыванию метрики сходства двух изображений
1.3.2.1 Сравнение между собой двух дескрипторов изображений и вычисление метрики по базе
В практической реализации алгоритма используется косинусовая метрика M(x,y)=\frac{dot(x,y)}{\lVert x \lVert * \lVert y \lVert}. Заметим, что вектора x, y уже нормированы на предыдущем этапе. Поэтому число операций для вычисления метрики составляет d умножений и d - 1 сложений, где d - размерность дескриптора. В практической реализации размерность дескриптора 128. Если размер базы n, то число операций O(n*d+n*(d-1))=O(n*d).
1.3.2.2 Агрегация результатов по людям
Для выполнения операции unique (без использования дополнительной памяти) необходимо отсортировать элементы (person_id, match_score) массива по ключу person_id, а при совпадении по score. После этого можно за линейное время удалить дубликаты по person_id, оставив первый элемент (который будет максимальным по match_score). Сложность таких операций O(n*logn+n)=O(n*logn).
1.3.2.3 Cортировка по убыванию метрики сходства двух изображений
Финальная сортировка по match_score будет выполнена за O(n*logk), где k - количество результатов в выдаче. Обычно на практике число k не более 1000, поскольку обработка результата чаще всего производится вручную оператором.
2 Практическая реализация системы
Построение биометрических шаблонов выполнено при помощи библиотеки распознавания лиц FaceSDK. В этом разделе приводится эффективность параллельной реализации сравнения изображени лица с некоторой базой лиц.
2.1 Быстрое сравнение биометрических шаблонов
При выполнении оценки производительности системы использовалась простая реализация cosine метрики (цикл для вычисления скалярного произведения) и с использованием FMA инстукций. Набор инструкций FMA позволяет выполнять операцию y = ax + b без дополнительных операций.
Псевдокод операции mm256_fmadd (intel)
FOR j := 0 to 7
i := j*32
dst[i+31:i] := (a[i+31:i] * b[i+31:i]) + c[i+31:i]
ENDFOR
dst[MAX:256] := 0
В результате тестирования (процессор 6300HQ, ноутбук, база 30М биометрических шаблонов) однопоточной программы было установлено, что FMA3 версия в 5 раз быстрее по сравнению с обычным циклом (880ms vs 4600ms). Все дальнейшие экспериенты будут проводиться с FMA3 реализацией (если не указано иначе). Компиляция производится gcc 5.4 с флагами -O3 -static-libgcc -static-libstdc++ -mavx -mavx2 -mfma -fopenmp
Применение openmp позволило ускорить версию с обычным циклом до 1300ms, что медленнее FMA3. Вычисление в несколько потоков не ускорило реализацию на FMA3. Вероятно, причина в пропускной способности оперативной памяти - для DDR4 15GBps на канал. Объем тестовой базы 15.5GB, поэтому не менее 500ms должно было занять чтение из памяти.
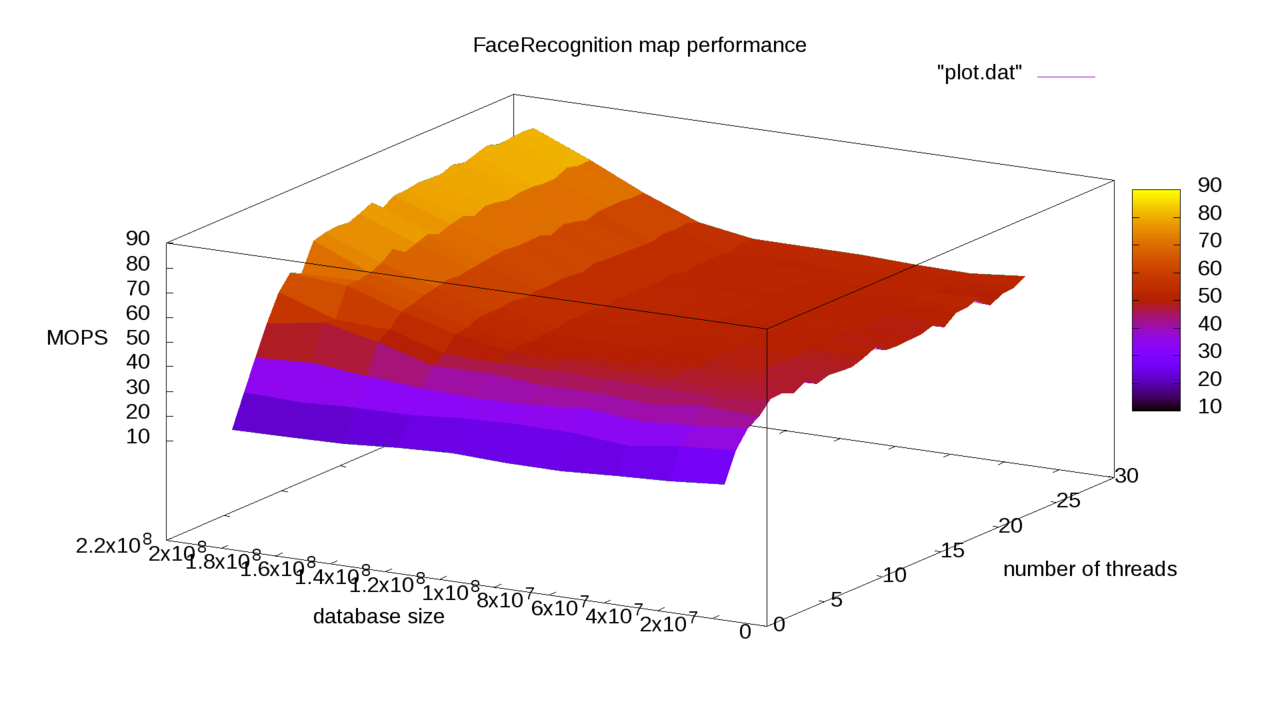
На сервере (2x E5-2683v3 256GB RAM, база 150М биометрических шаблонов) получилось следующее ускорение от использования FMA3 + OpenMP (MOPS - количество операций сравнения в секунду):
Также в процессе тестирования было замечено, что при превышении размера базы лиц объема оперативной памяти, напрямую доступной одному из процессоров, скороость работы снижается.
Количество операций с плавающей точкой (умножения) для сравнения биометрических шаблонов: n*128 FLOP.
2.2 Быстрое формирование результата
Если на каждой операции поиска изображения в базе необходимо выбирать максимальную фотографию для каждого челокека в базе, то задача сводится к классической map/reduce:
- map - вычисление скалярных произведений
- reduce - группировка результатов по людям и выдача N максимально похожих
В reduce применение openmp позволило увеличить скорость с 3000ms до 1000ms на 4 ядрах процессора (ноутбук с 6300HQ, 30M записей в базе)
Из дальшейнего фрагмента кода очевидно, что при таком распараллеливании нет зависимостей по переменным. Эксперимент показал, что применять openmp для inplace_merge неэффективно для текущих ограничений на размер базы (200-300M).
vector<MatchResult> OMP_Blob::reduce(size_t top_k, bool merge_person)
{
const int num_chunks = static_cast<int>(_chunks.size());
vector<MatchResult> result;
vector<vector<MatchResult>> results(num_chunks);
#pragma omp parallel for num_threads(_num_threads)
for(int i = 0; i < num_chunks; ++i) {
results[i] = _chunks[i].reduce(top_k, merge_person, false);
}
for(int i = 0; i < num_chunks; ++i) {
result.insert(result.end(), results[i].begin(), results[i].end());
}
if(merge_person) {
size_t csum = 0;
for(int i = 0; i < num_chunks; ++i) {
inplace_merge(result.begin(), result.begin() + csum, result.begin() + csum + results[i].size(), [](const MatchResult &a, const MatchResult &b) {
return a.person_id < b.person_id || (a.person_id == b.person_id && a.score > b.score);
});
csum += results[i].size();
}
result.resize(unique(result.begin(), result.end(), [](const MatchResult &a, const MatchResult &b) {
return a.person_id == b.person_id;
}) - result.begin());
}
size_t result_size = min(top_k, result.size());
partial_sort(result.begin(), result.begin() + result_size, result.end(), [](const MatchResult &a, const MatchResult &b) {
return a.score > b.score;
});
result.resize(result_size);
result.shrink_to_fit();
return result;
}
Финальную сортировку результатов по score ускорять не требуется, поскольку top_k на практике не более 1000.