High Performance Conjugate Gradient (HPCG) benchmark: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
VadimVV (обсуждение | вклад) |
Konshin (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
== Описание свойств и структуры алгоритма == | == Описание свойств и структуры алгоритма == | ||
| − | === | + | === Общее описание алгоритма === |
HPCG является тестом, разработанным для тестирования производительности компьютерных систем. По сути это генерирование некоторой системы линейных алгебраических уравнений (СЛАУ) <math>A \vec{x} = \vec{b}</math> с разрежённой квадратной положительно определённой симметричной матрицей <math>A</math> и вектором <math>\vec{b}</math>, с последующим решением этой СЛАУ. В качестве метода решения выбран один из методов сопряжённых направлений, основанных на ортогонализации последовательностей Крылова: метод сопряжённых градиентов с предобуславливателем Гаусса-Зейделя. В качестве тестируемой СЛАУ используется дискретизация уравнения диффузии в 3-мерной области с такими условиями на границе и в правой части, чтобы правильное решение СЛАУ состояло из одних единиц. При этом на одну строку (столбец) приходится по 27 ненулевых элементов («внутри» матрицы) и от 7 до 18 на «приграничных» строках и столбцах. Всего в тесте 48 384 000 линейных уравнений, причём матрица содержит 1 298 936 872 ненулевых элемента. | HPCG является тестом, разработанным для тестирования производительности компьютерных систем. По сути это генерирование некоторой системы линейных алгебраических уравнений (СЛАУ) <math>A \vec{x} = \vec{b}</math> с разрежённой квадратной положительно определённой симметричной матрицей <math>A</math> и вектором <math>\vec{b}</math>, с последующим решением этой СЛАУ. В качестве метода решения выбран один из методов сопряжённых направлений, основанных на ортогонализации последовательностей Крылова: метод сопряжённых градиентов с предобуславливателем Гаусса-Зейделя. В качестве тестируемой СЛАУ используется дискретизация уравнения диффузии в 3-мерной области с такими условиями на границе и в правой части, чтобы правильное решение СЛАУ состояло из одних единиц. При этом на одну строку (столбец) приходится по 27 ненулевых элементов («внутри» матрицы) и от 7 до 18 на «приграничных» строках и столбцах. Всего в тесте 48 384 000 линейных уравнений, причём матрица содержит 1 298 936 872 ненулевых элемента. | ||
Версия 17:51, 24 марта 2015
Содержание
- 1 Описание свойств и структуры алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Описание схемы реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Описание входных и выходных данных
- 1.10 Свойства алгоритма
- 2 Программная реализация
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Описание локальности данных и вычислений
- 2.3 Возможные способы и особенности реализации параллельного алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
1 Описание свойств и структуры алгоритма
1.1 Общее описание алгоритма
HPCG является тестом, разработанным для тестирования производительности компьютерных систем. По сути это генерирование некоторой системы линейных алгебраических уравнений (СЛАУ) A \vec{x} = \vec{b} с разрежённой квадратной положительно определённой симметричной матрицей A и вектором \vec{b}, с последующим решением этой СЛАУ. В качестве метода решения выбран один из методов сопряжённых направлений, основанных на ортогонализации последовательностей Крылова: метод сопряжённых градиентов с предобуславливателем Гаусса-Зейделя. В качестве тестируемой СЛАУ используется дискретизация уравнения диффузии в 3-мерной области с такими условиями на границе и в правой части, чтобы правильное решение СЛАУ состояло из одних единиц. При этом на одну строку (столбец) приходится по 27 ненулевых элементов («внутри» матрицы) и от 7 до 18 на «приграничных» строках и столбцах. Всего в тесте 48 384 000 линейных уравнений, причём матрица содержит 1 298 936 872 ненулевых элемента.
1.2 Математическое описание
Исходные данные: разрежённая квадратная положительно определённая симметричная матрица A (элементы a_{ij}), вектор правой части \vec{b} (элементы b_i). В реальности они не вполне входные (элементы матрицы генерирует сама программа), но для разбора общей схемы алгоритма удобно считать их входными данными.
Вычисляемые данные: вектор решения \vec{x} (элементы x_i), вектор \vec{r} (элементы r_i) невязки.
Детальные формулы отдельных частей алгоритма здесь описывать не будем, поскольку они являются самостоятельными алгоритмами и их детальные описания должны быть выполнены раздельно. Поэтому здесь будет приведена только общая схема алгоритма. Обращаем внимание на то, что в учебной литературе обычно приводится схема метода сопряжённых градиентов без предобуславливателя. Введение предобуславливателя объясняется тем, что без него матрица системы A \vec{x} = \vec{b} может быть плохо обусловленной, и это увеличивает необходимое для окончания работы метода сопряжённых градиентов количество итераций сверх меры. Дело в том, что, хотя метод сопряжённых градиентов по своему построению и математическому обоснованию является прямым (то есть у него известно количество операций, после которого он наверняка сойдётся к решению), но из-за того, что он использует точные формулы, выполняющиеся в процессах ортогонализации только в точной арифметике, появляющаяся неустойчивость настолько критична, что становится необходимым уменьшить количество итераций по сравнению с верхней теоретической оценкой. Это возможно только существенным уменьшением обусловленности матрицы системы с помощью матрицы M, называемой пере(пред-)обуславливателем. Эта матрица должна быть «приближением» матрицы A и в то же время легко обращаться. Тогда вместо плохо обусловленной СЛАУ A \vec{x} = \vec{b} будет решаться хорошо обусловленная СЛАУ M^{-1} A \vec{x} = M^{-1} \vec{b}. Само собой, фактической замены СЛАУ никто не производит, поскольку матрица M^{-1} A не является разрежённой. Вместо этого «умножение на M^{-1}» производят, когда в методе сопряжённых уравнений переходят от невязок \vec{r}_i к векторам M^{-1} \vec{r}_i.
Стартовая часть: программа генерирует матрицу A в некотором структурном виде и вектор правой части b.
Начало процесса: вычисляется стартовый вектор невязки \vec{r}_0 = \vec{b} - A \vec{x}_0, в качестве другого стартового вектора p_0 используется вектор x_0.
После этого стартует циклический процесс. Номер исполнения тела цикла обозначим i. В цикле выполняются следующие операции:
- Выполняется вычисление предобусловленной невязки z_i := M^{-1} \vec{r}_{i - 1}. Это происходит в три этапа, в которых используется разбиение матрицы A на две треугольные и диагональную (L - нижний треугольник A, U - верхний треугольник A, D — диагональ A (а также диагональ матриц L и U), так что A = L + U - D, U = L^T):
- Вычисляется \vec{t} = L^{-1} \vec{r}_{i - 1}
- Вычисляется \vec{s} = \vec{r}_{i-1} - (L - D) \vec{t}
- Вычисляется \vec{z}_i = U^{-1} \vec{s}.
- После этого вычисляются вектор p_i и вспомогательные скаляры по формулам:
- если i = 1, то
- \begin{align} \vec{p}_1 & = \vec{z}_1 \\ \alpha_1 & = (\vec{r}_0, \vec{z}_1) \end{align}
- иначе
- \begin{align} \alpha_i & = (\vec{r}_{i-1}, \vec{z}_i) \\ \beta_i & = \frac{\alpha_i}{\alpha_{i - 1}} \\ \vec{p}_i & = \beta_i \vec{p}_{i - 1} + \vec{z}_i \end{align}
- Затем вычисляются новые приближения к вектору решения и невязки:
- \begin{align} \gamma_i & = \frac{\alpha_i}{(\vec{p}_i,A \vec{p}_i)} \\ \vec{x}_i & = \vec{x}_{i - 1} + \gamma_i \vec{p}_i \\ \vec{r}_i & = \vec{r}_{i - 1} - \gamma_i A \vec{p}_i \end{align}
- В заключение цикла вычисляется || \vec{r}_i ||_2 и сравнивается с установленным пределом ошибки. Если норма ниже предела, процесс прерывается.
1.3 Вычислительное ядро алгоритма
Саму генерацию матрицы и правой части мы в алгоритм включать не будем. Вычислительное ядро алгоритма состоит из следующих крупных операций:
- Вычисление стартовой невязки
- и затем циклически:
- «прямая» обратная подстановка для решения СЛАУ с нижней треугольной матрицей,
- новое вычисление «невязки», но не с полной, а с нижней треугольной матрицей,
- обратная подстановка для решения СЛАУ с верхней треугольной матрицей,
- вычисление скалярного произведения 2 векторов,
- вычисление взвешенной суммы двух векторов,
- вычисление произведения матрицы на вектор,
- вычисление скалярного произведения двух векторов,
- вычисление взвешенной суммы двух векторов,
- вычисление квадратичной нормы вектора.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, макроструктура алгоритма состоит в последовательном выполнении следующих макроопераций:
- Вычисление стартовой невязки,
- и затем циклически:
- «прямая» обратная подстановка для решения СЛАУ с нижней треугольной матрицей,
- новое вычисление «невязки», но не с полной, а с нижней треугольной матрицей,
- обратная подстановка для решения СЛАУ с верхней треугольной матрицей,
- вычисление скалярного произведения 2 векторов,
- вычисление взвешенной суммы двух векторов,
- вычисление произведения матрицы на вектор,
- вычисление скалярного произведения двух векторов,
- вычисление взвешенной суммы двух векторов,
- вычисление квадратичной нормы вектора.
1.5 Описание схемы реализации последовательного алгоритма
Математическое описание алгоритма описано выше. При этом в ходе вычислений, реализующих какое-либо вычисление произведений матрицы на вектор (включая вычисления невязок или решения треугольных СЛАУ) следует учитывать, что для вектора размерности n каждая его компонента умножается не более чем на 27 элементов матрицы.
1.6 Последовательная сложность алгоритма
Поскольку для вектора размерности n каждая его компонента умножается не более чем на 27 элементов матрицы, то все макрооперации, связанные с умножением матрицы на вектор, имеют линейную последовательную сложность с коэффициентом 27 (или менее). Вычисления скалярных произведений (в т. ч. квадратичной нормы невязки) также линейны по последовательной сложности. Таким образом, общая последовательная сложность алгоритма линейна. Коэффициент пропорциональности между n и сложностью в общем случае зависит не только от разрежённости матриц, но и от количества итераций, требуемых для достижения требуемой точности решения.
В одном вычислении невязки для конкретных матриц теста сложность составит около 27 n операций типа «умножить и сложить». Вычисление скалярного произведения даёт порядка n таких операций. Таким образом, для тела цикла последовательная сложность составит порядка 112 n операций умножения и сложения.
1.7 Информационный граф
Граф состоит из информационных графов своих основных частей, поэтому здесь нет смысла приводить его целиком: совместное представление только усложнило бы общую картину, которую, вне сомнения, следует изучать по графам отдельных частей - методов, составляющих этот алгоритм. При этом следует отметить, что одной из таких отдельных частей будет вычисление предобусловленной невязки, а не её внутренние части типа решения треугольных СЛАУ и невязки треугольной матрицы. Это связано с тем, что эти внутренние части вычисления предобусловленной невязки хорошо стыкуются друг с другом.
1.8 Описание ресурса параллелизма алгоритма
При изучении ресурса параллелизма видно, что основная сложность (линейная) будет у вычислений скалярных произведений. Остальные части алгоритма в силу разреженности матриц имеют не более постоянной сложности с небольшим коэффициентом. Поэтому для оптимизации вычислений нужно заняться именно оптимизацией вычисления скалярных произведений.
1.9 Описание входных и выходных данных
По сути теста у него всегда одни и те же данные, причём вычисляемые в самом же тесте. Поэтому в строгом смысле у алгоритма нет входных данных.
Выходными данными являются вычисляемые и выдаваемые тестом нормы невязки, решения, матрицы и их отношения, а также вычисляемая мощность вычислений целевой вычислительной системы.
1.10 Свойства алгоритма
2 Программная реализация
2.1 Особенности реализации последовательного алгоритма
2.2 Описание локальности данных и вычислений
2.2.1 Описание локальности реализации алгоритма
2.2.1.1 Описание структуры обращений в память и качественная оценка локальности
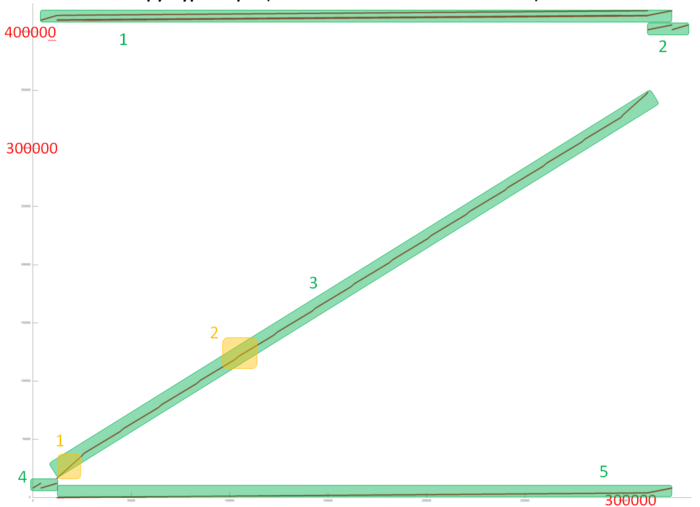
На рисунке 12.1 представлен общий профиль обращений в память для теста HPCG. В данном тесте выполняются операции над разреженной матрицей, поэтому большая часть элементов массивов не задействуются (поскольку являются нулевыми). В результате объем задействованной памяти (около 350-400 тысяч обращений) меньше общего числа обращений, т.е. в среднем к каждому элементу было выполнено менее 1 обращения. Данный профиль можно разбить на несколько фрагментов, которые выделены на рис. 12.1 зеленым цветом.
Сразу отметим, что, поскольку в данной программе задействовано очень большое число массивов, мы не можем получать отдельные профили для каждого фрагмента и визуализировать их независимо. Поэтому мы используем фильтрацию общего профиля для получения нужного подмножества обращений. В этом случае графики для фрагментов остаются такими же, как и при независимо построении. Также номер обращения всегда начинается с нуля. Однако значения по оси ординат остаются соответствующими общему профилю и потому начинаются не с нуля.
Фрагмент 1 представлен на рис. 12.2. Он устроен достаточно сложно, однако явно обладает регулярной структурой. Для ее понимания рассмотрим отдельно ее различные части, выделенные на рисунке оранжевым цветом.
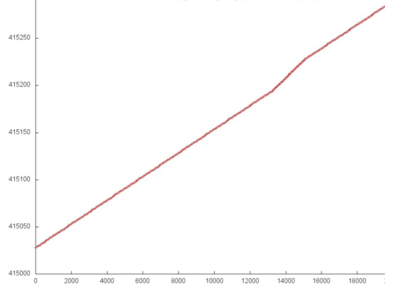
При ближайшем рассмотрении можно увидеть, что часть 1, как и подобная ей часть 3, представляют собой обычный последовательный перебор элементов, возможно, с некоторым небольшим шагом по памяти. На рис. 12.3 представлена область из середины части 2. Можно заметить, что в данном случае также выполняется последовательный перебор элементов, однако шаг по памяти нерегулярный. По всей видимости, это связано с нерегулярностью наполненности разреженной матрицы.
В данном случае нерегулярность перебора элементов не влияет на локальность. Поэтому можно сказать, что части 1-3 обладают высокой пространственной локальностью, поскольку используется шаг по памяти, однако очень низкой временной локальностью, поскольку повторные обращения просто отсутствуют.
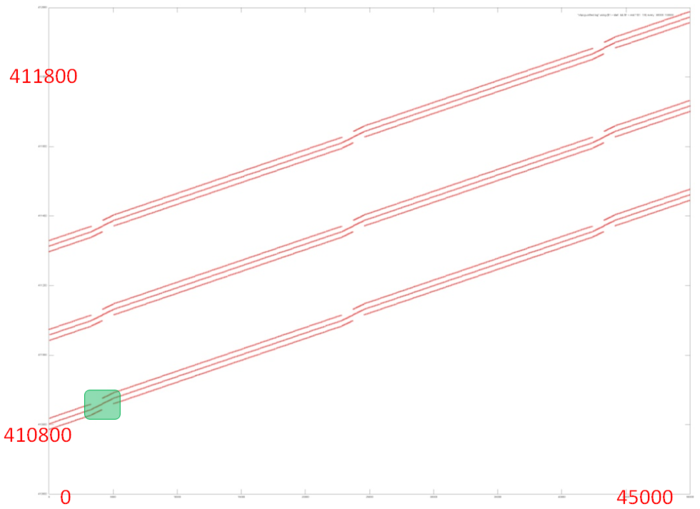
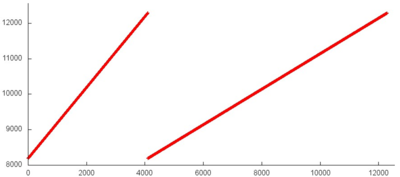
На рис. 12.4 представлена область из середины части 4. При таком приближении заметно, что часть 4 состоит из трех параллельно идущих профилей, каждый из которых состоит из набора подобных итераций, выполняемых над другим набором элементов. Каждый итерация, в свою очередь, состоит из трех параллельно идущих переборов с одинаковым шагом (поскольку наклон линий одинаков).
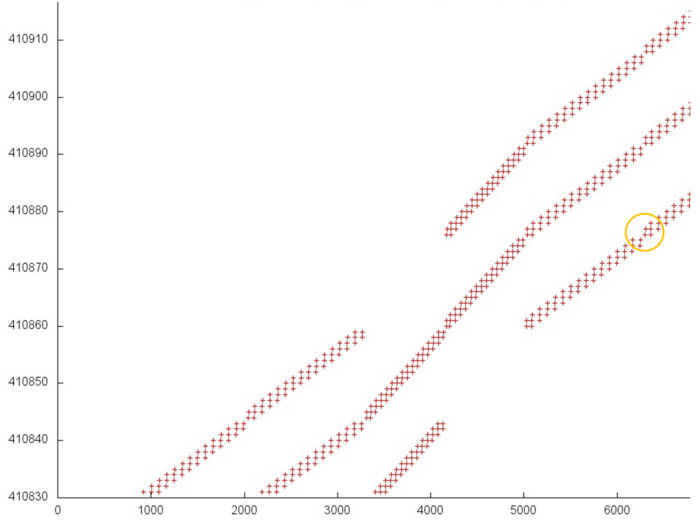
Рассмотрим более подробно область около перехода от одной итерации к другой (рис. 12.5). Видно, что каждая итерация устроена заметно сложнее, чем просто последовательный перебор, однако регулярность обращений подтверждается. Каждый из трех параллельно идущих переборов итерации состоит из набора фрагментов с одинаковой структурой; переход от одного от одного фрагмента к следующему выделен на рисунке оранжевым кругом. Каждый такой небольшой фрагмент представляет собой последовательный перебор с шагом 1, однако на каждом шаге перебора происходит 3 обращения к идущим подряд элементам.
Переход от одной итерации к другой устроен похожим образом, только меняется число параллельно выполняемых переборов.
В целом видно, что часть 4 характеризуется высокой пространственной локальностью – обращения в каждой части выполняются к соседним элементам. При этом временная локальность также высока, поскольку повторные обращения происходят достаточно часто.
В результате про фрагмент 1 можно сказать, что он обладает хорошей пространственной локальностью, поскольку во все частях основным является последовательный перебор или его более сложный аналог. Про временную локальность сделать выводы сложнее, однако, с достаточно большой вероятностью, она тоже достаточно высока, поскольку основная часть обращений сосредоточена в части 4.
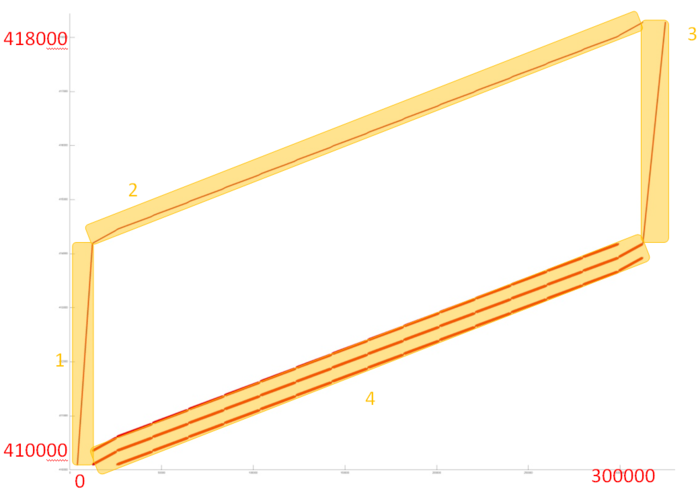
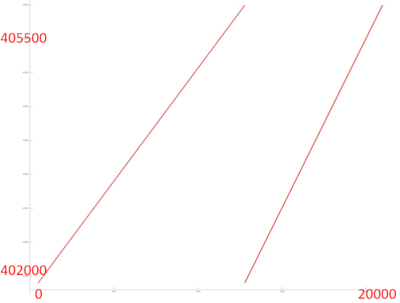
Теперь перейдем к рассмотрению фрагмента 2, профиль обращений которого показан на рис. 12.6. Видно, что данный фрагмент состоит из существенно меньшего числа обращений, чем предыдущий фрагмент, и состоит из двух этапов, каждый из которых похож на перебор элементов массива. Более подробный анализ показывает, что в обоих случаях действительно выполняется обычный простой последовательный перебор с фиксированным шагом. Более того, шаг по памяти у них одинаков, а разный наклон вызван тем, что параллельно с первым перебором выполняется больше обращений к другим массивам, в результате чего кажется, что данный перебор выполняется дольше.
Подобный фрагмент обладает высокой пространственной и низкой временной локальностью.
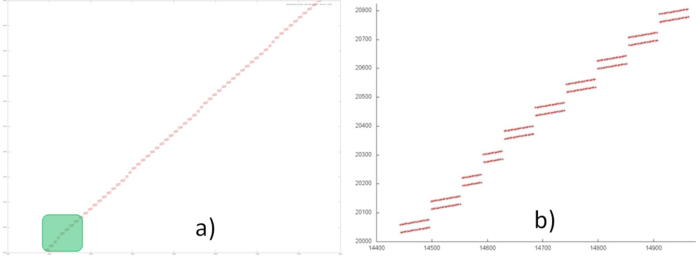
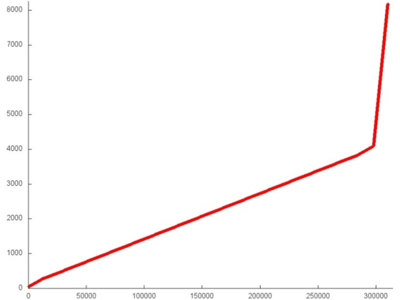
Фрагмент 3, который задействует наибольший диапазон данных в программе, напоминает перебор элементов с нерегулярным шагом, о чем говорит ломаный характер линии. Отметим, что из рис. 12.1 нельзя понять, не обладает ли на самом деле эта линия более сложным строением. Однако можно предположить, что основная часть фрагмента обладает схожей структурой, а в начале и конце данного фрагмента находятся две похожие области, которые явно отличаются от остальной части. Поэтому рассмотрим отдельно две части, отмеченные на рис. 12.1 оранжевым цветом.
При более близком рассмотрении части 1 (рис. 12.7a) становится понятным, что фрагмент 3 обладает более сложной структурой, чем простой перебор с нерегулярным шагом. Можно заметить наличие подобных областей, которые имеют разный размер, однако по виду схожую структуру. Если выполнить дальнейшее приближение (рис. 12.7b, приближение выделенного зеленым участка на рис. 12.7a), мы увидим, что, действительно, данные небольшие области подобны и представляют собой два параллельно выполняемых перебора элементов.
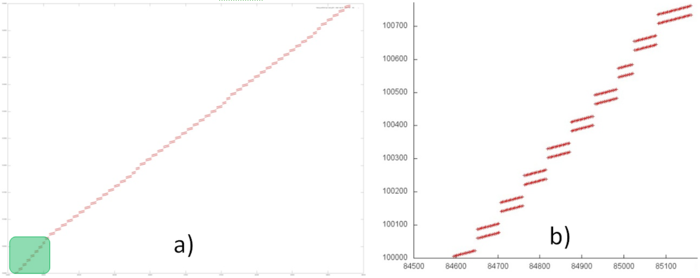
Подробное рассмотрение показывает, что часть 2 фрагмента 3 очень похожей структурой (рис. 12.8). Более того, шаг по памяти примерно одинаков, поэтому можно предположить, что две данные части на самом деле однотипны. В этом случае разница в их представлении на рис. 12.1 вызвана разным числом обращений к другим массивам: одновременно с частью 1 выполнялось меньше обращений к другим массивам, поэтому на графике угол наклона этой части кажется больше.
Таким образом, можно сказать, что данный фрагмент обладает достаточно высокой пространственной локальностью, поскольку зачастую следующее обращение происходит к соседнему элементу, и не очень высокой временной локальностью, поскольку число повторных обращений достаточно мало, хотя они и расположены близко друг к другу.
Фрагмент 4, представленный на рис. 12.9, обладает ровно такой же структурой, что и фрагмент 2; меняется только число обращений, и как следствие, вероятно, число задействованных элементов.
Перейдем к рассмотрению последнего фрагмента. На рис. 12.10 явно выделяется две области, однако в данном случае, также как и в остальных фрагментах, изменение в угле наклона связано с параллельно выполняемыми обращениями к другим массивам, и на самом деле структура двух областей одинакова.
При дальнейшем рассмотрении становится понятным, что данный профиль на самом деле представляет собой обычный последовательный перебор элементов с шагом 1.
В целом общий профиль рассматриваемой программы обладает непростой и не всегда регулярной структурой, поэтому сложно делать предположения относительно локальности в целом. Однако если резюмировать полученные выводы по фрагментам, можно предположить следующее, что пространственная локальность всего профиля достаточно высока, поскольку часто встречаются последовательные переборы; при этом временная локальность, наоборот, достаточно низка, так как повторные обращения встречаются нечасто.
2.2.1.2 Количественная оценка локальности
Реализация, на основе которой были получены количественные оценки, приведена здесь (данная реализация взята отсюда). Условия запуска описаны здесь.
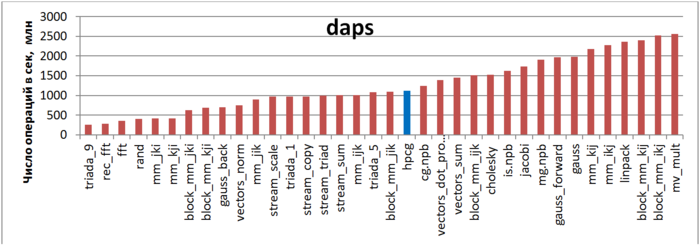
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рисунке 12.11 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что, несмотря на работу с разреженной матрицей, данная программа показывает достаточно высокие результаты, значительно выше теста со случайным доступом (rand) или обратного хода метода Гаусса решения СЛАУ (gauss_back).
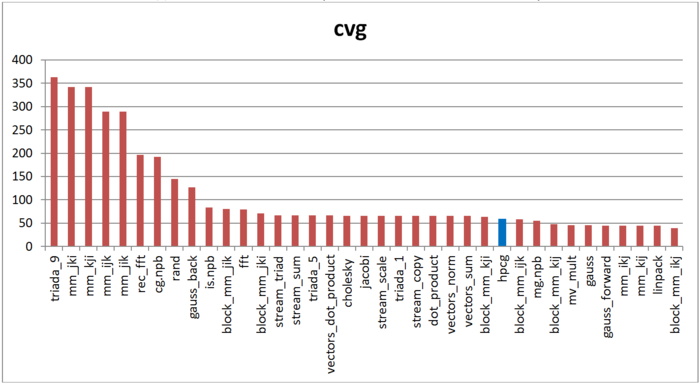
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рисунке 12.12 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, результаты hpcg даже несколько лучше по сравнению с оценкой daps. В первую очередь это связано с высокой пространственной локальностью, однако означает, что и временная локальность не так уж низка.
2.3 Возможные способы и особенности реализации параллельного алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Описание масштабируемости алгоритма
2.4.2 Описание масштабируемости реализации алгоритма
Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:
- число процессоров [4 : 256]
- размер матрицы [1024 : 5120]
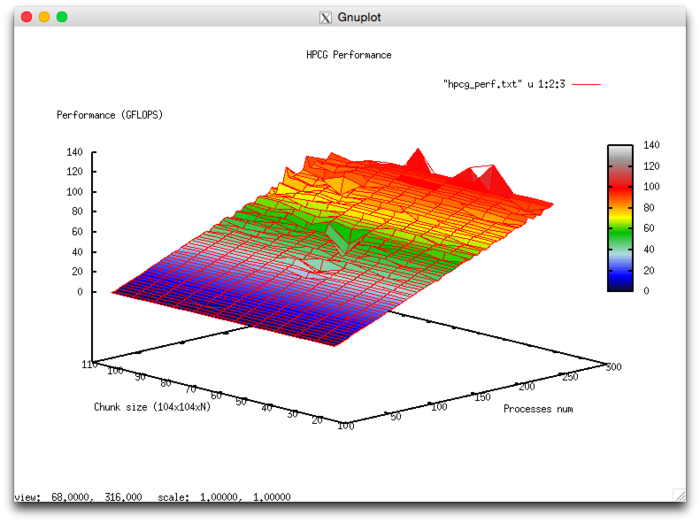
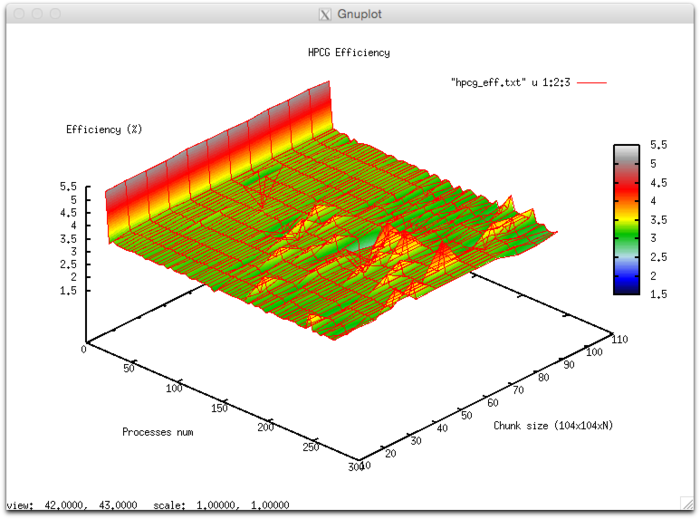
Эффективность выполнения реализации алгоритма
- Минимальная эффективность 0,11 %
- Максимальная эффективность 6.65%
Оценка масштабируемости
- По числу процессов: -0.000101 – при увеличении числа процессов эффективность в целом уменьшается по рассматриваемой области, хотя и менее интенсивно, чем при увеличении числа процессов. Учитывая разницу между максимальным и минимальным значением эффективности в 6,5% можно сделать вывод, что на рассмотренной области снижение эффективности, скорее всего, достаточно равномерное. Снижение эффективности объясняется тем, что при росте вычислительной сложности существенно возрастают объемы передаваемых данных. Могут присутствовать области возрастания эффективности, на всех рассмотренных размерах матрицы. Это может объясняться увеличением вычислительной сложности задачи, что при постоянных накладных расходах на организацию параллельного взаимодействия приводит к общему увеличению эффективности работы.
- По размеру задачи:-0.00674– при увеличении размера задачи эффективность в целом уменьшается по рассматриваемой области. Это может свидетельствовать о том, что при увеличении размера задачи возрастают и накладные расходы на организацию параллельного взаимодействия. Так как интенсивность снижения эффективности по этому направлению выше, чем по направлению числа процессов, скорее всего падение интенсивности значительно при малом числе процессов более интенсивное, чем в присутствующих областях возрастания эффективности при большом числе процессов.
- По двум направлениям: -6.621e-05 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, однако интенсивность уменьшения эффективности очень мала. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров составляет почти 6,5 % говорит о том, что если на поверхности присутствуют области с очень интенсивным изменением эффективности, но очень малые по площади. На остальной поверхности изменения эффективности незначительны и находятся на приблизительно одном и том же уровне.
Исследованная реализация теста
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Существующая реализация теста одна. При этом следует отметить важный момент: для параллельных систем версия программы представляет собой алгоритм, отличающийся от последовательного. Разработчиками заявлено, что это сделано для оптимизации распараллеливания программы, и при этом количество требующихся для сходимости к нужной точности итераций увеличивается в сравнении с последовательной версией. Таким образом, под одним названием существуют как минимум 2 алгоритма.