Участник:Pandvik/Ортогонализация Грама - Шмидта

Авторы описания алгоритма: Павлов Андрей, Филимонов Владимир.

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

В конечномерном евклидовом пространстве существует ортонормированный базис.

Для доказательства этого факта требуется находить и строить такие базисы. Построить ортонормированный базис можно, отталкиваясь от некоторого исходного базиса, при помощи алгоритма, который называют процессом ортогонализации Грама — Шмидта.

Процесс ортогонализации Грама-Шмидта используется для квадратных невырожденных матриц, которые преобразуются, либо уже преобразованы, к верхнему(нижнему) треугольному виду.

Процесс ортогонализации Грама-Шмидта нашёл применение в оптимизации оценивания параметров моделей управления объектом, в протоколах безопасности, в обработке сигналов, в вычислении локальных минимумов целочисленных решёток и многом другом.

Обычно, процесс ортогонализации используется как промежуточный шаг в других алгоритмах для уменьшения количества вычислений.

1.2 Математическое описание алгоритма

Исходные данные: квадратная матрица A с линейно независимыми векторами $\mathbf{a}_1,...,\mathbf{a}_N$.

Определяется оператор проекции $\mathbf{proj}_b a = \frac{\left \langle a,b \right \rangle}{\left \langle b,b \right \rangle }b$, где $\left \langle a,b \right \rangle$ - скалярное произведение векторов a и b. Данный оператор используется для проецирования вектора a коллинеарно вектору b.

$\mathbf{b}_1 = \mathbf{a}_1$

$\mathbf{b}_2 = \mathbf{a}_2 - \mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_2$

$\mathbf{b}_3 = \mathbf{a}_3 - \mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_3 - \mathbf{proj}_{\mathbf{b}_2} \mathbf{a}_3$

$\mathbf{b}_4 = \mathbf{a}_4 - \mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_4 - \mathbf{proj}_{\mathbf{b}_2} \mathbf{a}_4 - \mathbf{proj}_{\mathbf{b}_3} \mathbf{a}_4$

$\vdots$

$\mathbf{b}_N = \mathbf{a}_N - \sum_{j=1}^{N-1} \mathbf{proj}_{\mathbf{b}_j} \mathbf{a}_N$

На основе каждого вектора $\mathbf{b}_j (j = 1 \cdots N)$ может быть получен нормированный вектор $\mathbf{e}_j = \frac{\mathbf{b}_j}{||\mathbf{b}_j||}$.

Результаты процесса ортогонализации Грама-Шмидта: $\mathbf{b}_1\cdots\mathbf{b}_N$ - система ортогональных векторов либо система ортонормированных векторов $\mathbf{e}_1\cdots\mathbf{e}_N$.

1.3 Вычислительное ядро алгоритма

Основная вычислительная сложность данного алгоритма заключается в вычислении суммы проекций векторов $\sum_{j=1}^{i-1} \mathbf{proj}_{\mathbf{b}_j} \mathbf{a}_N$, на основе которой получается $b_i$.

Подробное описание общей сложности алгоритма представлено в разделе #Последовательная сложность алгоритма

1.5 Схема реализации последовательного алгоритма

1. $\mathbf{b}_1 = \mathbf{a}_1$

2. $\mathbf{b}_i = \mathbf{a}_i - \sum_{j=1}^{i-1} \mathbf{proj}_{\mathbf{b}_{j}} \mathbf{a}_i$ при $i = 2 \cdots N$, где для каждого $\mathbf{proj}_b a$ выполняется $\frac{\left \langle a,b \right \rangle}{\left \langle b,b \right \rangle}b$.

1.6 Последовательная сложность алгоритма

Последовательный алгоритм требует:

${\color{Blue}\bullet} \quad \frac{n(n-1)}{2}n$ - вычитаний;

${\color{Blue}\bullet} \quad \frac{n(n-1)}{2}n$ - делений;

${\color{Blue}\bullet} \quad n \cdot 2 \cdot (n-1)(n-2)$ - умножений.

Исходя из вышесказанного, получаем итоговую сложность последовательного алгоритма $O(n^3)$.

1.7 Информационный граф

Опишем информационный граф алгоритма.

Для вычисления $b_i$ требуется найти $proj_{b_{j}}a_{i}$ для всех $j \in [1, i]$. Следовательно для полного вычисления вектора $b_{i}$ требуется знать все $b_{j}$ с меньшим индексом. Такая зависимость по данным очень не удачна для параллелизма. Однако, если разбить процесс вычисления $b_{i}$ на несколько этапов, соответствующих функциям проекции ($proj_{b_{j}}a_{i}$), то это позволит производить некоторые предварительные вычисления для $b_{j}$ до момента, когда станут известны все предшествующие ей $b_{i}$.

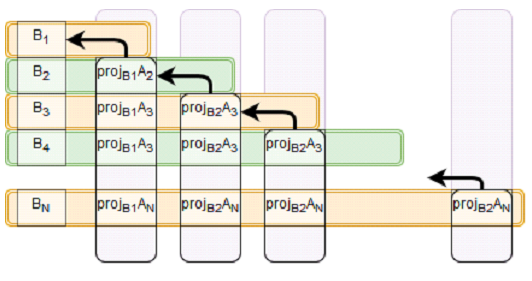
На Рис. 1 изображена зависимость каждого из этапов от предыдущих вычислений. Первая строка овалов содержит все проекции, зависящие от $b_{1}$, вторая строка - все проекции, зависящие от $b_{2}$, $\;\cdots\;$ самая верхняя строка содержит проекцию, которая зависит от $b_{N-1}$.

Рис. 2 показывает зависимость по данным немного в другом формате. Каждая строка представляет собой набор данных, которые требуются для вычисления $b_{i}$ из первого столбца. Второй и последующие столбцы группируют проекции, зависящие от одной из $b_{i}$ и, с помощью стрелки, показывают эту зависимость.

Рис. 1. Информационный граф алгоритма Грама-Шмидта

Рис. 2. Информационный граф алгоритма Грама-Шмидта

1.8 Ресурс параллелизма алгоритма

На основе графа зависимости по данным, представленном на Рис. 1 или Рис. 2 раздела #Информационный граф можно выделить следующий ресурс параллелизма. После вычисления $b_{i}$ можно начинать параллельно вычислять все $proj_{b_i}a_{j}$. На Рис. 2 блоки, которые можно вычислять параллельно представлены столбцами.

Кроме того, при очень больших размерностях можно также распараллелить вычисление проекций. Так как в функции проекции участвует пара векторов $a$ и $b$, а сама операция проекции определяется как $\mathbf{proj}_b a = \frac{\left \langle a,b \right \rangle}{\left \langle b,b \right \rangle }b$, где $\left \langle a,b \right \rangle$ - скалярное произведение векторов $a$ и $b$, то с помощью использования векторных операций можно получить некоторый выигрыш в производительности.

1.8.1 Оценка ускорения параллельной реализации алгоритма

Рассмотрим случай, когда присутствует возможность запуска бесконечного числа потоков. Попробуем оценить сложность вычисления ортогональных векторов, при условии, что параллельно будут запускаться все проекции использующие одинаковую $b_i$. В этом случае, останется критический путь зависимости по данным: $b_1 \leftarrow proj_{b_2}a_{2} \leftarrow b_2 \leftarrow proj_{b_3}a_{3} \leftarrow \ldots \leftarrow proj_{b_{N-1}}a_{N-1} \leftarrow b_N$. Следовательно для оценки сложность распараллеленной версии алгоритма достаточно почитать сложность представленной цепочки вычислений.

${\color{Blue}\bullet} \quad N \cdot 3$ умножения в одной проекции;

${\color{Blue}\bullet} \quad (N-1) \cdot 2$ сложения и 1 деление.

В цепочке зависимости данных присутствует $N-1$ проекция, значит всего:

${\color{Blue}\bullet} \quad N \cdot N \cdot 3$ - умножений;

${\color{Blue}\bullet} \quad N \cdot (N-1) \cdot 2$ - сложений;

${\color{Blue}\bullet} \quad N \cdot 1$ - делений.

Получаем итоговую сложность $O(N^{2})$.

1.9 Входные и выходные данные алгоритма

Входные данные: квадратная матрица A (элементы $\mathbf{a}_{ij}$). Матрица может быть приведена к верхнему(нижнему) треугольному виду.

Ограничение: матрица A должна быть невырожденной.

Объём входных данных: $\frac{n(n+1)}{2}$ (после преобразования матрицы к треугольному виду достаточно хранить только ненулевые элементы).

Выходные данные: матрица B (система ортогональных векторов $\mathbf{b}_{1} \cdots \mathbf{b}_{N}$).

Объём выходных данных: $\frac{n(n+1)}{2}$ (в силу треугольного вида матрицы).

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейной(последовательная реализация - $O(n^3)$, параллельная реализация - $O(n^2)$).

Отношение числа операций к суммарному объему входных и выходных данных - линейное.

В силу теоремы о существовании ортонормированного базиса в результате работы алгоритма получаем систему из, минимум, одного линейно независимого ортогонального(ортонормированного) вектора. Из-за различных способов приведения исходной матрицы к треугольному виду(в случае использования разных методов или библиотек), а также ошибок округления в самом начале алгоритма ортогонализации могут получаться различные ортогональные(ортонормированные) системы в итоге.

2 ЧАСТЬ. Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Пример реализации базового алгоритма с использованием технологий OpenMP и MPI представлен в статье .

Существует реализация процесса отртогонализации Грама-Шмидта, которая является вычислительно более устойчивой, такая реализации имеет название Модифицированный процесс Грама-Шмидта.