Участник:Sergey Lavrushkin/EM-алгоритм кластеризации: различия между версиями
| Строка 1: | Строка 1: | ||
| + | {{algorithm | ||
| + | | name = EM-алгоритм кластеризации | ||
| + | | serial_complexity = <math>O(nkq^2)</math> | ||
| + | | pf_width = <math>O(nk)</math> | ||
| + | | input_data = <math>nq + 1</math>. | ||
| + | | output_data = <math>k(n + q^2 + q + 1)</math> | ||
| + | }} | ||
| + | |||
Автор статьи: [[Участник: Sergey Lavrushkin|Сергей Лаврушкин]] (группа 620) | Автор статьи: [[Участник: Sergey Lavrushkin|Сергей Лаврушкин]] (группа 620) | ||
Версия 19:16, 15 октября 2016
| EM-алгоритм кластеризации | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(nkq^2)[/math] |
| Объём входных данных | [math]nq + 1[/math]. |
| Объём выходных данных | [math]k(n + q^2 + q + 1)[/math] |
| Параллельный алгоритм | |
| Ширина ярусно-параллельной формы | [math]O(nk)[/math] |
Автор статьи: Сергей Лаврушкин (группа 620)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
1.1.1 EM-алгоритм
EM-алгоритм (англ. expectation-maximization) — алгоритм, используемый в математической статистике для нахождения оценок максимального правдоподобия параметров вероятностных моделей, в случае, когда модель зависит от некоторых скрытых переменных. Каждая итерация алгоритма состоит из двух шагов. На E-шаге (expectation) вычисляется ожидаемое значение функции правдоподобия, при этом скрытые переменные рассматриваются как наблюдаемые. На M-шаге (maximization) вычисляется оценка максимального правдоподобия, таким образом увеличивается ожидаемое правдоподобие, вычисляемое на E-шаге. Затем это значение используется для E-шага на следующей итерации. Алгоритм выполняется до сходимости.[1]
Как правило, ЕМ-алгоритм применяется для решения задач двух типов:
- К первому типу можно отнести задачи, связанные с анализом действительно неполных данных, когда некоторые статистические данные отсутствуют в силу каких-либо причин.
- Ко второму типу задач можно отнести те задачи, в которых функция правдоподобия имеет вид, не допускающий удобных аналитических методов исследования, но допускающий серьезные упрощения, если в задачу ввести дополнительные «ненаблюдаемые» (скрытые, латентные) переменные. Примерами прикладных задач второго типа являются задачи распознавания образов, реконструкции изображений. Математическую суть данных задач составляют задачи кластерного анализа, классификации и разделения смесей вероятностных распределений.
Алгоритм основан на методике итеративного вычисления оценок максимального правдоподобия, предложенной в 1977 г. (A. P. Demster, N. M. Laird, D. B. Rubin. Maximum Likelihood from Incomplete Data via the EM Algorithm).[2]
1.1.2 Кластеризация с помощью EM-алгоритма
Кластеризация — задача разбиения заданной выборки объектов (ситуаций) на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались [3]. В основе идеи применения EM-алгоритма для кластеризации лежит предположение, что исследуемое множество данных может быть смоделировано с помощью линейной комбинации многомерных нормальных распределений, а целью является оценка параметров распределения, которые максимизируют логарифмическую функцию правдоподобия, используемую в качестве меры качества модели. К оцениваемым параметрам относятся математические ожидания и ковариационные матрицы. Предполагается, что любое наблюдение принадлежит ко всем кластерам, но с разной вероятностью. Задача заключается в "подгонке" распределений смеси к данным, а затем в определении вероятностей принадлежности наблюдения к каждому кластеру. Наблюдение должно быть отнесено к тому кластеру, для которого данная вероятность выше.
Алгоритм EM основан на вычислении расстояний. Он может рассматриваться как обобщение кластеризации на основе анализа смеси вероятностных распределений. В процессе работы алгоритма происходит итеративное улучшение решения, а остановка осуществляется в момент, когда достигается требуемый уровень точности модели. Мерой в данном случае является монотонно увеличивающаяся статистическая величина, называемая логарифмическим правдоподобием.[4]
1.2 Математическое описание алгоритма
Исходные данные:
- [math]k[/math] — число кластеров,
- [math]X =\{x_{1}, x_{2}, ..., x_{n}\}[/math] — множество из [math]n[/math] наблюдений [math]q[/math]-мерного пространства.
Вычисляемые данные:
- [math](w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)[/math] — параметры смеси гауссовых распределений,
- [math]Y[/math] — матрица размера [math]n \times k[/math] с вероятностями членства в кластерах.
1.2.1 Постановка задачи разделения смеси гауссовых распределений
Пусть [math]w_1, ..., w_k[/math] — априорные вероятности кластеров, [math]p_1(x), ..., p_k(x)[/math] — плотности распределения кластеров. Тогда плотность распределения вектора признаков [math]x[/math] сразу по всем кластерам равна:
- [math] \begin{align} p(x) = \sum_{j=1}^{k}w_jp_j(x) \end{align} [/math]
Необходимо на основе выборки оценить параметры модели [math]w_1, ..., w_k, p_1(x), ..., p_k(x)[/math]. Это позволит оценивать вероятность принадлежности к кластеру и, таким образом, решить задачу кластеризации. Такая задача называется задачей разделения смеси распределений:
- [math] \begin{align} p(x) = \sum_{j=1}^{k}w_jp_j(x),\quad p_j(x) = \phi(\theta_j; x), \end{align} [/math]
где [math]\theta_j[/math] — параметры распределения [math]p_j(x)[/math]. В случае смести гауссовых распределений предполагается, что все компоненты имеют многомерное нормальное распределение. То есть в случае [math]q[/math]-мерного пространства признаков [math]\phi(\theta_j; x)[/math] имеют следующий вид:
- [math] \begin{align} & \phi(\theta_j; x) = \frac{1}{\Big(2\pi\Big)^{\frac{q}{2}}\sqrt{|\Sigma_j|}}\exp{\bigg\{-\frac{\delta^2}{2}\bigg\} },\\ & \delta^2 = \Big( x - \mu_j \Big)^T \Sigma_j^{-1} \Big( x - \mu_j \Big), \end{align} [/math]
где:
- [math]\Sigma_j[/math] — ковариационная матрица размером [math]q \times q[/math],
- [math]\mu_j[/math] — [math]q[/math]-мерный вектор математических ожиданий,
- [math]\delta^2[/math] — квадратичное расстояние Махаланобиса.
В случае смеси гауссовых распределений получаем, что [math]\theta_j = (\mu_j, \Sigma_j)[/math]. То есть для решения задачи разделения смеси гауссовых распределений необходимо оценить вектор параметров [math](w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)[/math]. Согласно принципу максимизации правдоподобия:
- [math] \begin{align} w, \theta = \underset{w, \theta}{\operatorname{argmax}} \sum_{i=1}^{n}\ln{p(x_i)} = \underset{w, \theta}{\operatorname{argmax}} \sum_{i=1}^{n}\ln{\sum_{j=1}^{k}w_jp_j(x_i)} \end{align} [/math]
Таким образом, имеет место задача максимизации суммы логарифмов сумм, решение которой представляет большую трудность. В таком случае полезным оказывается итеративный метод решения — EM-алгоритм.[5]
1.2.2 EM-алгоритм
Оптимальные параметры задачи разделения смеси гауссовых распределений отыскиваются последовательно с помощью итерационного EM-алгоритма. Основная идея – вводится вспомогательный вектор скрытых переменных. Это позволяет свести сложную оптимизационную задачу к последовательности итераций по пересчету коэффициентов (скрытых переменных по текущему приближению вектора параметров - E-шаг) и максимизации правдоподобия (с целью найти следующее приближение вектора - М-шаг).[6]
EM-алгоритм заключается в следующем:
- В начале работы алгоритма задаются параметры начального приближения. Наиболее общим способом инициализации является присвоение элементам матрицы математических ожиданий случайных значений [math] \mu_j \leftarrow Random [/math], начальные ковариационные матрицы определяются как единчиные [math]\Sigma_j \leftarrow I[/math], веса кластеров задаются одинаковыми [math]w_i \leftarrow \frac{1}{k}[/math]. Также в качестве начальных параметров можно использовать результат работы алгоритма K-means. (Данная эвристика применяется, так как K-means требуется намного меньше итераций до достижения стабилизации, в то время как каждый шаг EM требует больших вычислительных затрат).
- Далее итеративно выполняется следующая пара процедур:
- E-шаг: используя текущее значение вектора параметров [math](w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)[/math], вычисляем значение вектора скрытых переменных [math]y[/math]:
- [math] \begin{align} & y_{ij} = \frac{w_j p_j(x_i)}{\sum_{l=1}^{k}w_lp_l(x_i)} \end{align} [/math]
- М-шаг: переоценка вектора параметров, используя текущее значение вектора скрытых переменных:
- [math] \begin{align} & n_j = \sum_{i = 1}^{n}y_{ij}, \\ & \mu_j^{new} = \frac{1}{n_j} \sum_{i = 1}^{n}y_{ij}x_i, \\ & \Sigma_j^{new} = \frac{1}{n_j} \sum_{i = 1}^{n}y_{ij}(x_i - \mu_j^{new})(x_i - \mu_j^{new})^T,\\ & w_j^{new} = \frac{n_j}{n}. \end{align} [/math]
- E-шаг: используя текущее значение вектора параметров [math](w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)[/math], вычисляем значение вектора скрытых переменных [math]y[/math]:
Итерации происходят до сходимости (норма разности векторов скрытых переменных или изменение логарифмического правдоподобия на каждой итерации не будет превышать заданную константу) или достижения максимального числа итераций.
1.3 Вычислительное ядро алгоритма
В вычислительное ядро EM-алгоритма входят:
- Вычисление скрытых переменных [math]y_{ij}[/math] на E-шаге (всего их [math]nk[/math]).
- Переоценка вектора параметров [math](w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)[/math] на M-шаге, используя текущие значения скрытых переменных [math]y_{ij}[/math].
1.4 Макроструктура алгоритма
Как записано в описании ядра алгоритма, основную часть метода составляют множественные вычисления скрытых переменных [math]y_{ij}[/math] на E-шаге и обновление вектора параметров [math](w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)[/math] на M-шаге. Также стоит выделить вычисление определителя и обратной матрицы ковариационных матриц [math]\Sigma_j[/math] в начале E-шага.
1.5 Схема реализации последовательного алгоритма
Последовательная реализация алгоритма EM может быть проиллюстрирована с помощью следующего псевдокода:
- Инициализация: установка начальных значений [math]\mu, \, \Sigma_j \, (j = \overline{1, k}), \, w[/math].
- Пока изменение логарифмического правдоподобия [math]\Delta llh \geq \epsilon[/math] и не достигнуто максимальное число итераций [math]m[/math], выполнять шаги E и M.
Шаг E
def E-step:
Инициализировать нулевыми значениями [math]\mu^{'}, \, \Sigma_j^{'} \, (j = \overline{1, k}), \, w^{'}, \, llh[/math]
for [math]j = \overline{1, k}[/math]:
Вычислить определитель и обратную матрицу матрицы [math]\Sigma_j[/math]
for [math]i = \overline{1, n}[/math]:
[math]sump_i = 0[/math]
for [math]j = \overline{1, k}[/math]:
[math]\delta_{ij} = \big( x_i - \mu_j \big)^T \Sigma_j^{-1} \big( x_i - \mu_j \big)[/math]
[math]g_{ij} = \frac{w_j}{{2 \pi}^\frac{q}{2}|\Sigma_j|}\exp{\big\{-\frac{\delta^2}{2}\big\} }[/math]
[math]sump_i \mathrel{+}= g_{ij}[/math]
[math]y_i = \frac{g_i}{sump_i}[/math]
[math]llh \mathrel{+}= \ln(sump_i)[/math]
[math]\mu^{'} \mathrel{+}= x_iy_i^T[/math]
[math]w^{'} \mathrel{+}= y_i[/math]
Шаг M
def M-step:
for [math]j = \overline{1, k}[/math]:
[math]\mu_j = \frac{\mu_j^{'}}{w_j^{'}}[/math]
for [math]i = \overline{1, n}[/math]:
[math]\Sigma_j^{'} \mathrel{+}= (x_i - \mu_j)y_{ij}(x_i - \mu_j)^T[/math]
[math]\Sigma_j = \frac{\Sigma_j^{'}}{w_j^{'}}[/math]
[math]w = \frac{w^{'}}{n}[/math]
Логаририфмическое правдоподобие вычисляется как:
- [math] \begin{align} llh=\sum_{i=1}^{n}\ln{(sump_i)} \end{align} [/math]
Матрицы [math]\mu^{'}, \, \Sigma_j^{'} \, (j = \overline{1, k}), \, w^{'}[/math] являются временными и используются только для вычислений.
1.6 Последовательная сложность алгоритма
Последовательная сложность одной итерации EM-алгоритма:
- E-шаг:
В случае недиагональных ковариационных матриц сложность вычислений:- Определителей ковариационных матриц [math]|\Sigma_j|[/math] ([math]j = \overline{1, k}[/math]) методом Гаусса: [math]O(kq^3)[/math],
- Матриц, обратных ковариационным матрицам [math]\Sigma_j^{-1}[/math] ([math]j = \overline{1, k}[/math]) методом Гаусса-Жордана: [math]O(kq^3)[/math],
- Скрытых переменных [math]y_{ij}[/math] ([math]i = \overline{1, n}, j = \overline{1, k}[/math]): [math]O(nkq^2)[/math].
- Определителей ковариационных матриц [math]|\Sigma_j|[/math] ([math]j = \overline{1, k}[/math]): [math]O(kq)[/math],
- Матриц, обратных ковариационным матрицам [math]\Sigma_j^{-1}[/math] ([math]j = \overline{1, k}[/math]): [math]O(kq)[/math],
- Скрытых переменных [math]y_{ij}[/math] ([math]i = \overline{1, n}, j = \overline{1, k}[/math]): [math]O(nkq)[/math].
-
М-шаг:
В случае недиагональных ковариационных матриц сложность вычислений:- Обновление математических ожиданий [math]\mu_j[/math] ([math]j = \overline{1, k}[/math]): [math]O(nkq)[/math],
- Обновление ковариационных матриц [math]\Sigma_j[/math] ([math]j = \overline{1, k}[/math]): [math]O(nkq^2)[/math],
- Обновление весов кластеров [math]w_j[/math] ([math]j = \overline{1, k}[/math]): [math]O(nk)[/math].
- Обновление математических ожиданий [math]\mu_j[/math] ([math]j = \overline{1, k}[/math]): [math]O(nkq)[/math],
- Обновление ковариационных матриц [math]\Sigma_j[/math] ([math]j = \overline{1, k}[/math]): [math]O(nkq)[/math],
- Обновление весов кластеров [math]w_j[/math] ([math]j = \overline{1, k}[/math]): [math]O(nk)[/math].
Таким образом, последовательная сложность итерации EM-алгоритма в случае недиагональных ковариационных матриц имеет порядок [math]O(kq^3 + nkq^2)[/math], а в случае диагональных ковариационных матриц — [math]O(nkq)[/math]. При этом, обычно размерность элементов выборки [math]q[/math], также как и число кластеров [math]k[/math], значительно меньше числа элементов выборки [math]n[/math] ([math]k \ll n, q \ll n[/math]), поэтому в случае недиагональных ковариационных матриц сложность может быть записана в виде [math]O(nkq^2)[/math].
1.7 Информационный граф
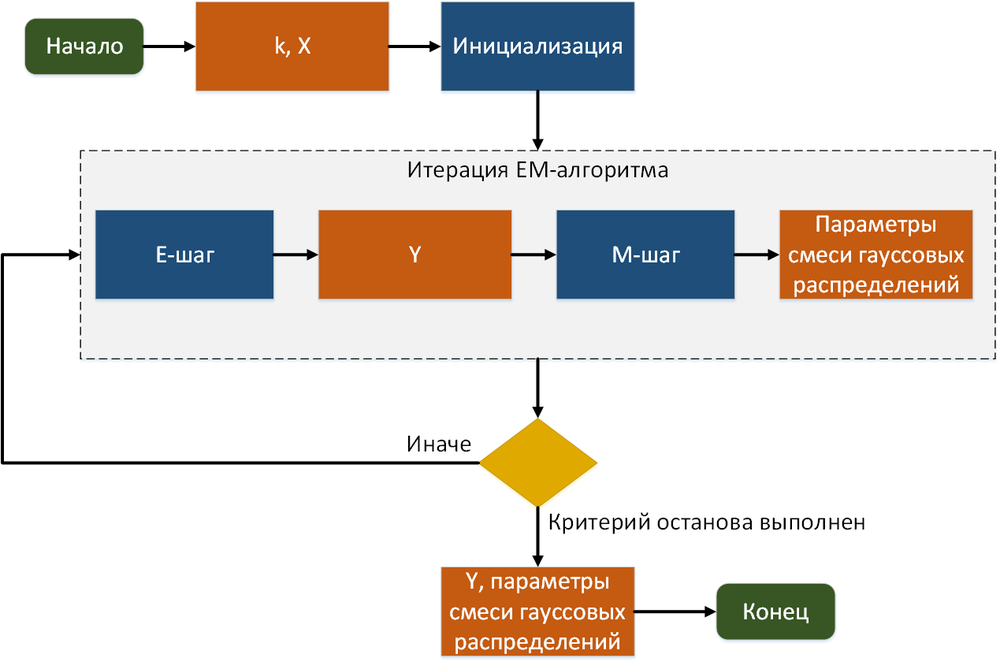
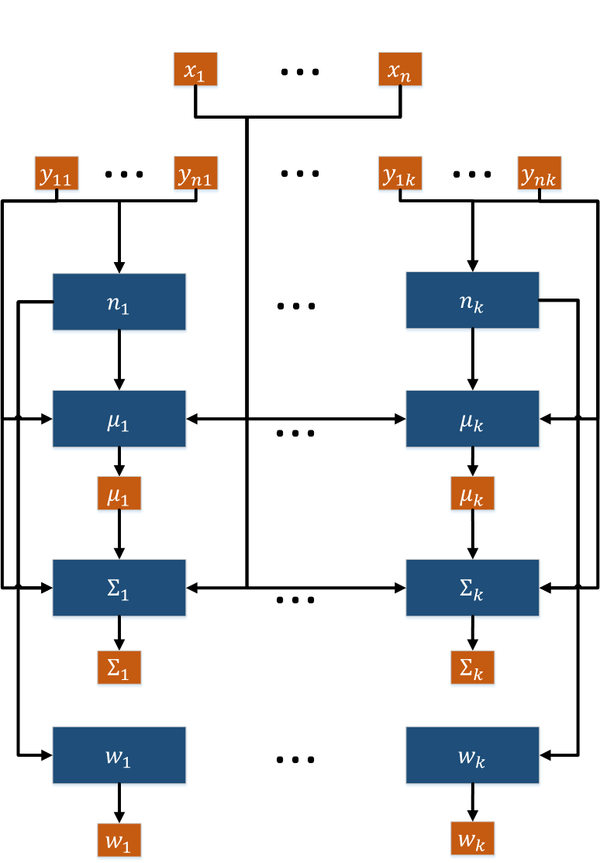
Граф алгоритма в терминах E-шагов и M-шагов представлен на рис. 1. Каждая итерация алгоритма зависит от результата работы предыдущей итерации, M-шаг зависит от результата E-шага.
Рассмотрим по отдельности информационные графы E-шага и M-шага.
1.7.1 E-шаг
Опишем граф E-шага как аналитически, так и в виде рисунка.
Граф алгоритма состоит из четырех групп вершин:
- Первая группа вершин соответствует вычислению обратных матриц и определителей ковариационных матриц. Число вершин: [math]k[/math]. Аргументом этой операции является ковариационная матрица [math]\Sigma_j[/math]. Результат срабатывания операции является промежуточным данным алгоритма.
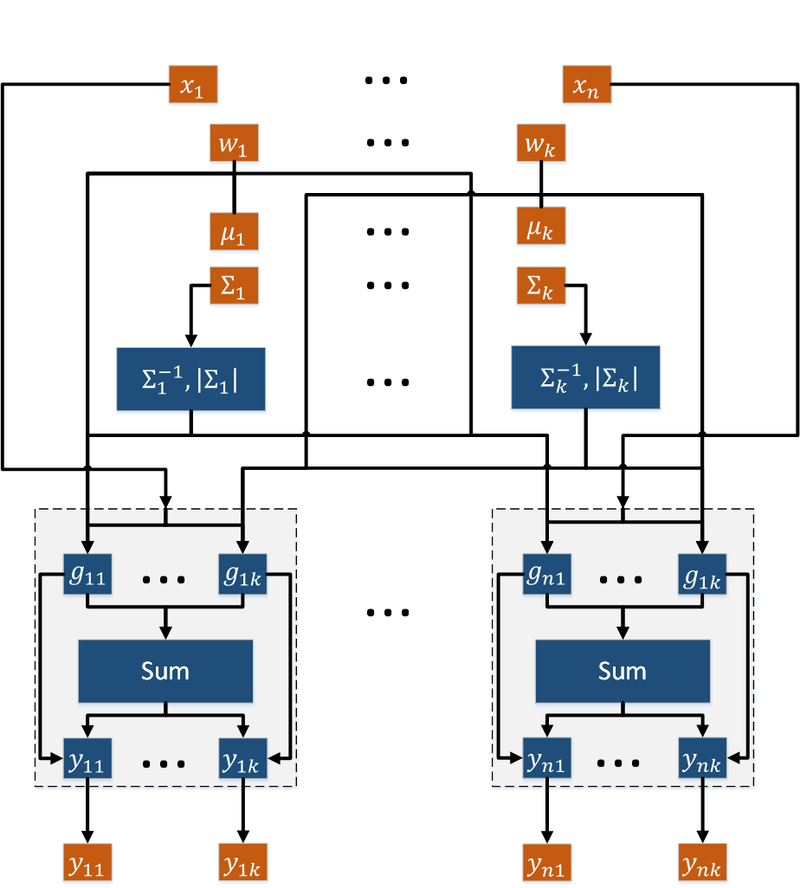
- Вторая группа вершин соответствует вычислению [math]g_{ij} = \frac{w_j}{{2 \pi}^\frac{q}{2}|\Sigma_j|}\exp{\big\{-\frac{1}{2} \big( x_i - \mu_j \big)^T \Sigma_j^{-1} \big( x_i - \mu_j \big) \big\}}[/math]. Число вершин: [math]nk[/math]. Аргументами этой операции являются вес кластера [math]w_j[/math], математическое ожидание [math]\mu_j[/math], ковариационная матрица [math]\Sigma_j[/math], наблюдение элемент выборки [math]x_i[/math]. Результат срабатывания операции является промежуточным данным алгоритма.
- Третья группа вершин соответствует вычислению нормировочных коэффициентов [math]\sum_{l=1}^{k}g_{ij}[/math]. Число вершин: [math]n[/math]. Аргументами этой операции являются значения [math]g_{ij}, \, j = \overline{1, k}[/math]. Результат срабатывания операции является промежуточным данным алгоритма.
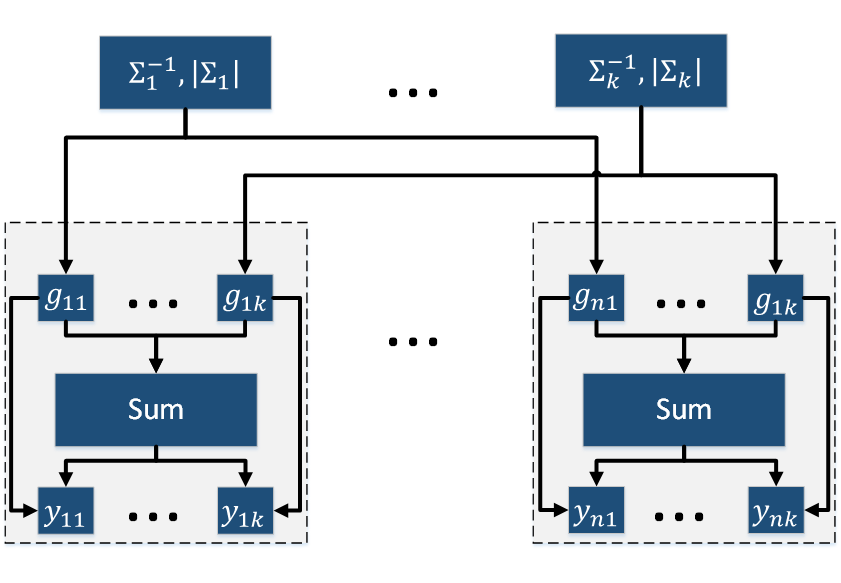
- Четвертая группа вершин соответствует вычислению скрытых переменных [math]y_{ij}[/math]. Число вершин: [math]nk[/math]. Аргументами этой операции являются значение [math]g_{ij}[/math] и нормировочный коэффициент. Результат срабатывания операции является выходным данным алгоритма.
Описанный граф представлен на рис.2 и рис.3. Здесь вершины одной группы расположены в одной строке. Вершины-операции обозначены синим цветом, вершины-данные — оранжевым.
1.7.2 M-шаг
Опишем граф M-шага как аналитически, так и в виде рисунка.
Граф алгоритма состоит из четырех групп вершин:
- Первая группа вершин соответствует вычислению нормировочных коэффициентов [math]n_j[/math]. Число вершин: [math]k[/math]. Аргументами этой операции являются скрытые переменные [math]y_{ij}, \, i = \overline{1, n}[/math]. Результат срабатывания операции является промежуточным данным алгоритма.
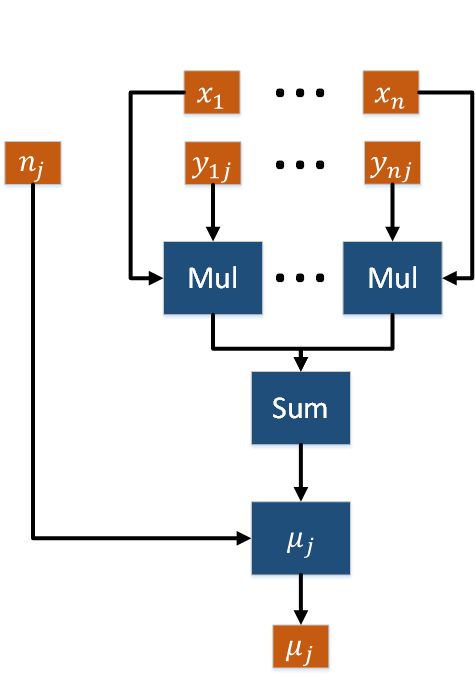
- Вторая группа вершин соответствует вычислению математических ожиданий [math]\mu_j[/math]. Число вершин: [math]k[/math]. Аргументами этой операции являются множество наблюдений [math]X[/math], скрытые переменные [math]y_{ij}, \, i = \overline{1, n}[/math], нормировочный коэффициент [math]n_j[/math]. Результат срабатывания операции является выходным данным алгоритма.
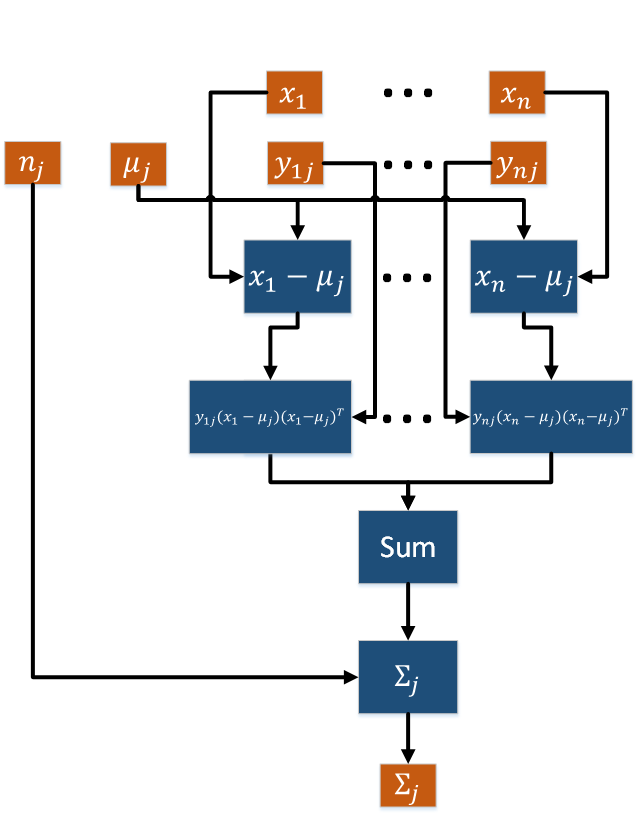
- Третья группа вершин соответствует вычислению ковариационных матриц [math]\Sigma_j[/math]. Число вершин: [math]k[/math]. Аргументами этой операции являются множество наблюдений [math]X[/math], скрытые переменные [math]y_{ij}, \, i = \overline{1, n}[/math], нормировочный коэффициент [math]n_j[/math], математическое ожидание [math]\mu_j[/math]. Результат срабатывания операции является выходным данным алгоритма.
- Четвертая группа вершин соответствует вычислению весов кластеров [math]w_{j}[/math]. Число вершин: [math]k[/math]. Аргументом этой операции является нормировочный коэффициент [math]n_j[/math]. Результат срабатывания операции является выходным данным алгоритма.
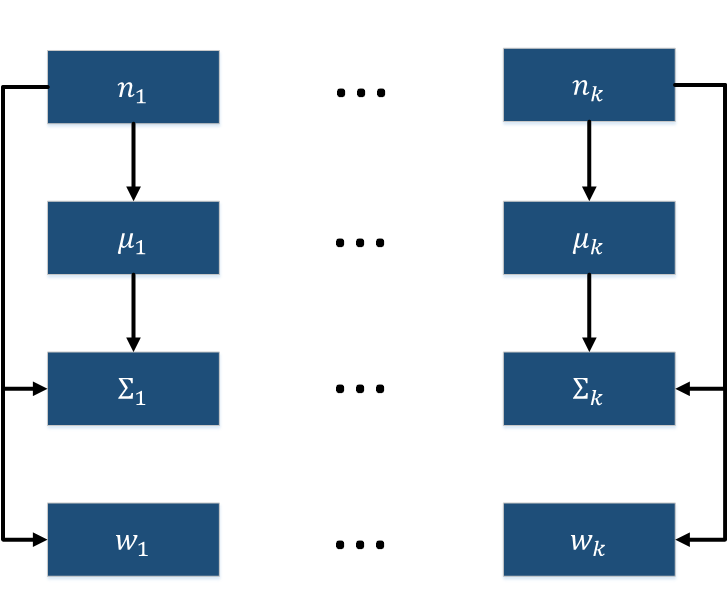
Описанный граф представлен на рис.4 и рис.5. Здесь вершины одной группы расположены в одной строке. Вершины-операции обозначены синим цветом, вершины-данные — оранжевым.
Графы вычисления математических ожиданий [math]\mu_j[/math] и ковариационных матриц [math]\Sigma_j[/math] представлены на рис. 6 и рис. 7.
1.8 Ресурс параллелизма алгоритма
По графам из пункта 1.7 видно, что скрытые переменные [math]y_{ij}[/math] в E-шаге, [math]y_{ij}x_i[/math] в вычислении математических ожиданий [math]\mu_{j}[/math] и [math]y_{ij}(x_i - \mu_j)(x_i - \mu_j)[/math] в вычислении ковариационных матриц [math]\Sigma_{j}[/math] в M-шаге вычисляются независимо ([math]i = \overline{1, n}, \, j = \overline{1, k}[/math]). Таким образом, при условии наличия неограниченного числа процессоров эти операции можно распараллелить как по числу наблюдений, так и по числу кластеров. Однако в отсутствии неограниченного числа процессорв целесообразно проводить распараллеливание по числу наблюдений, потому что, как правило, число наблюдений значительно больше числа кластеров ([math]n \gg q[/math]).
При классификации по ширине ЯПФ его сложность будет [math]O(nk)[/math]. Сложность ЯПФ при классификации по высоте зависит от способа вычисления обратных матриц и определителей ковариационных матриц, а также от способа суммирования при вычислении скрытых переменных и обновлении вектора параметров.
1.9 Входные и выходные данные алгоритма
Входные данные: [math]k[/math] — число кластеров; [math]X =\{x_{1}, x_{2}, ..., x_{n}\}[/math] — множество из [math]n[/math] наблюдений [math]q[/math]-мерного пространства.
Объем входных данных: [math]nq + 1[/math].
Выходные данные: [math](w, \theta) = (w_1, ..., w_k; \mu_1, ..., \mu_k; \Sigma_1, ..., \Sigma_k)[/math] — параметры смеси гауссовых распределений; [math]Y[/math] — матрица размера [math]n \times k[/math] с вероятностями членства в кластерах.
Объем выходных данных: [math]k(n + q^2 + q + 1)[/math].
1.10 Свойства алгоритма
Алгоритм является недетерминированным. Число итераций до сходимости метода зависит от начального приближения и выбранного критерия останова.
1.10.1 Достоинства и недостатки алгоритма
Среди достоинств EM-алгоритма можно выделить следующие:
- Мощная статистическая основа.
- Линейное увеличение сложности при росте объема данных.
- Устойчивость к шумам и пропускам в данных.
- Возможность построения желаемого числа кластеров.
- Быстрая сходимость при удачной инициализации.
К недостаткам EM-алгоритма можно отнести следующее:
- Алгоритм неустойчив по начальным данным (то есть тем, которые инициализируют вектор параметров на первой итерации), так как он находит локальный экстремум, значение которого может оказаться гораздо ниже, чем глобальный максимум. В зависимости от выбора начального приближения алгоритм может сходиться к разным точкам. Также может сильно варьироваться скорость сходимости.
- Алгоритм не позволяет определять количество [math]k[/math] компонент смеси. Эта величина является структурным параметром алгоритма.
- Предположение о нормальности всех измерений данных не всегда выполняется.
2 Программная реализация алгоритма
2.1 Масштабируемость реализации алгоритма
2.2 Существующие реализации алгоритма
- OpenCV
- Armadillo — OpenMP реализация с предположением диагональности ковариационных матриц
- MLPack
- scikit-learn
- Matlab
- CUDA реализация №1
- CUDA реализация №2
3 Литература
<references \>
- ↑ ЕМ-алгоритм, его модификации и обобщения http://www.machinelearning.ru/
- ↑ A. Dempster, N. Laird and D. Rubin. Maximum likelihood estimation from incomplete data. – Journal of the Royal Statistical Society, Series B, 1977, vol. 39, p. 1-38.
- ↑ Кластеризация www.machinelearning.ru
- ↑ EМ — масштабируемый алгоритм кластеризации basegroup.ru
- ↑ Поиск структуры в данных — Lecture 9 — Expectation Maximization (EM-алгоритм) www.coursera.org
- ↑ EM алгоритм (пример) www.machinelearning.ru