Участник:JuliaA/Алгоритм кластеризации с использованием представлений

Основные авторы описания: Ю.А. Антохина, С.А. Шатков

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Пусть дан набор точек и заданы правила определения расстояния между ними. Задача кластеризации сгруппировать эти точки в определенное число кластеров. Члены одного кластера похожи, а члены разных классов различны.

В алгоритме CURE применяется иерархическая кластеризация. Есть два подхода к иерархической кластеризации. В одном случае один большой кластер на каждом шаге разбивается на несколько, пока число кластеров не будет равно заданному заранее числу кластеров. В другом случае наоборот кластеры, состоящие каждый из одной точки объединяются в большие. Второй метод используется в CURE.

Результат кластеризации зависит от того, как будут представлены кластеры. Например, средним всех точек кластера, или всеми точками кластера. Применение среднего возможно только в евклидовом пространстве. А использование всех точек неустойчиво к случайным выбросам. В CURE используется другой метод: для каждого кластера выбираются точки представители. Выбирается постоянное число точек, которые будут представлять каждый кластер. Кластеры с наиболее похожими наборами репрезентативных точек объединяются на каждом шаге алгоритма.

За счет использования точек представителей алгоритм CURE устойчив к выбросам и может выделять кластеры сложной формы и различных размеров.

Описание шагов

Шаг 1. Если все данные использовать сразу как входные для CURE, то эффективность алгоритма будет низкая, а время выполнения большим. Поэтому на первом шаге мы случайным образом выбираем часть точек которые помещаются в память, затем группируем наиболее похожие с помощью иерархического метода. Дальше работаем с кластерами.

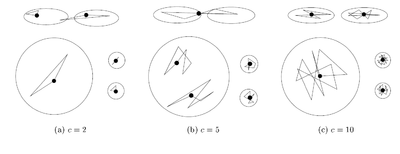
Шаг 2. Для каждого кластера выбираем [math]c[/math] точек представителей, максимально удаленных друг от друга. Чисто [math]c[/math] остается постоянным.

Шаг 3. Объединяем кластеры с наиболее похожими наборами точек представителей. Если не достигнуто нужное число кластеров, то перейти на шаг 2. Чтобы при объединении кластеров не выбирать каждый раз c точек представителей из всех точек, мы выбираем их только из [math]2c[/math] точек объединенных кластеров.

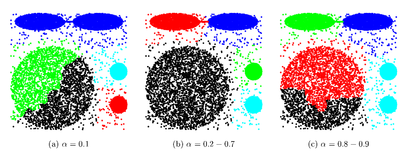
Выбранные точки сдвигаются на следующем шаге на [math]\alpha[/math] к центроиду кластера. Алгоритм становится основанным на методе поиска центроида при [math]\alpha = 1[/math], и основанным на всех точках кластера при [math]\alpha = 0[/math].

Пример работы алгоритма для разных параметров [math]\alpha[/math].

1.2 Математическое описание алгоритма

Пусть дана матрица [math]x \in R^{m\times n}[/math], количество кластеров [math]k[/math], число точек представителей [math]c[/math], параметр [math]\alpha[/math], параметр [math]\gamma[/math]. Каждая строка матрицы представляет собой точку в [math]n[/math] - мерном пространстве.

m число точек для кластеризации, n размерность.

Расстояние [math]\rho(p,k)[/math] между точками [math]p = (p_{1},\dots,p_{n})[/math] и [math]k = (k_{1},\dots,k_{n})[/math] будем вычислять по формуле:

[math]\rho(p,k) = \sqrt{\sum_{i=1}^n (p_{i} - k_{i})^2}[/math]

Шаг "Инициализация"

Выбираются [math]\lceil \gamma m\rceil[/math] строк матрицы случайным образом. Например, можно использовать Алгоритм R.

В основной памяти выделяется куча, часть которой используется для размещения дерева, листьями которого являются выбранные строки, соединённые ребром с вершиной дерева.

Шаг "Кластеризация"

В самом начале шага считаем каждую выбранную точку одноточечным кластером с центроидой в этой же точке.

Далее выполняем следующие шаги 1-2, пока количество кластеров не станет равно [math]k[/math]:

Шаг 1:

Для каждого [math]i[/math]-го кластера вычисляется центроида [math]\mu_{i}[/math] по формуле:

[math]\mu_{i} = \frac{1}{s_{i}}\sum_{j\in S_{i}} x^{j}[/math], где [math]S_{i}[/math] - номера строк матрицы [math]x[/math], входящие в [math]i[/math]-й кластер; [math]s_{i}[/math] - количество элементов в множестве [math]S_{i}[/math]; [math]x^{j}[/math] - [math]j[/math]-я строка матрицы [math]x[/math].

Шаг 2:

Выполняется поиск пары кластеров, "наиболее подходящих" для объединения. В качестве критерия выбора можно рассматривать: наименьшее расстояние между центроидами кластеров или наименьшее расстояние между элементами, входящими в рассматриваемую пару кластеров. Существуют также другие критерии выбора "подходящих" классов, например, сравнение плотности кластеров до объединения и после. Далее выполняется слияние найденных кластеров. Для дерева это означает добавление новой вершины, соединённой ребром с корнем; поддеревья кластеров становятся ветвями этой новой вершины.

Шаг "Назначение представителей"

На данном шаге для каждого кластера определяются [math]c[/math] точек-представителей. Для наилучшего отображения формы множества предполагается использование точек, максимально удалённых друг от друга.

Для этого используем следующий алгоритм:

Выберем произвольную точку кластера и назначим её представителем.

ПОКА количество представителей меньше [math]c[/math] ВЫПОЛНЯТЬ

 Назначаем представителем точку, наименьшее расстояние от которой до уже выбранных точек-представителей является максимальным среди всех оставшихся точек.

Шаг "Сдвиг представителей к центроиде"

Для каждого представителя выполняется сдвиг к центроиде соответствующего кластера в [math]\alpha[/math] раз.

Шаг "Присваивание"

На данном шаге происходит присвоение неиспользованных точек (строк матрицы [math]x[/math]) к кластерам. Для точки-строки [math]p[/math] вычисляется расстояние до каждого представителя. Результат: строка [math]p[/math] добавляется в поддерево кластера, которому принадлежит наиближайший представитель.

Результатом работы алгоритма является дерево, ветвями которого являются отдельные кластеры. Листьями кластеров являются строки из матрицы [math]x[/math].

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма представляет собой итерационное построение [math]k[/math] кластеров, вычисление их центроид и назначение точек-представителей.

1.4 Макроструктура алгоритма

Основную часть метода составляют разбиение случайной выборки строк на [math]k[/math] кластеров и нахождение точек-представителей для каждого кластера.

1.6 Последовательная сложность алгоритма

Максимальное время выполнения алгоритма [math]O(n^2 logn)[/math]. Для двумерного пространства временная сложность может быть [math]O(n^2)[/math]. Так что сложность алгоритма не хуже чем у центроидного. То есть при такой размерности входных данных CURE выполняется за полиномиальное время.

(ПОЯСНЕНИЯ, ЕСЛИ ЕСТЬ ВРЕМЯ)

1.9 Входные и выходные данные алгоритма

Входные данные: матрица [math]x \in R^{m\times n}[/math], количество кластеров [math]k[/math], число точек представителей [math]c[/math], параметр [math]\alpha[/math], параметр [math]\gamma[/math].

[math]m[/math] число точек для кластеризации, [math]n[/math] размерность.

Параметр [math]\alpha[/math] для сжатия точек представления к центру кластера. В оригинальной статье авторы показывают что [math]\alpha[/math] от [math]0.2[/math] до [math]0.7[/math] помогает хорошо выявлять несферические кластеры и подавлять редкие выбросы.

Параметр [math]\gamma[/math] задаёт какая часть от [math]m[/math] точек будет использована при случайной выборке точек на шаге "Инициализация".

Число точек представителей выбирается в зависимости от данных. Если возможно появление кластеров сложной формы, то точек должно быть больше, чтобы выявить их форму. В оригинальной статье авторы показывают что уже при [math]c[/math] равном [math]10[/math] достигается неплохая эффективность.

Пример работы алгоритма для разных параметров [math]c[/math].

1.10 Свойства алгоритма

Алгоритм CURE выполняет иерархическую кластеризацию с использованием набора определяющих точек. Он действует только в евклидовом пространстве и предназначен для кластеризации очень больших наборов числовых данных.

Преимущества: выполняет кластеризацию на высоком уровне даже при наличии выбросов, выделяет кластеры сложной формы и различных размеров, обладает линейно зависимыми требованиями к месту хранения данных и квадратичную временную сложность для данных высокой размерности.

Недостатки: есть необходимость в задании пороговых значений и количества кластеров, работает только на числовых данных, эффективен только для данных низкой размерности

2 ЧАСТЬ. Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Данный раздел будет заполнен к 15 ноября.

2.7 Существующие реализации алгоритма

Последовательная реализация CURE-алгоритма для кластеризации для Python/C++ представлена в пакете: pyclustering.

Также существует параллельная реализация алгоритма, описанная в сборнике [3]. Алгоритм предложенный в статье использует массив данных состоящий из размеров кластера, его центроида и репрезентативных точек, а при объединении кластеров информацию о новом кластере просто записывают в строчку предыдущего. Также для каждого алгоритма требуется считать индекс и расстояние до ближайшего кластера. Именно их поиск авторы статьи и предлагают распараллелить.

3 Литература

[1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.

[2] Sudipto Guha (Stanford), Rajeev Rastogi (Bell Labs), Kyuseok Shim (Korea Institute of Technology). CURE: an efficient clustering algorithm for large databases. SIGMOD '98 Proceedings of the 1998 ACM SIGMOD international conference on Management of data, pp 73-84

[3] Panagiotis E. Hadjidoukas, Laurent Amsaleg. OpenMP Shared Memory Parallel Programming. Volume 4315 of the series Lecture Notes in Computer Science pp 289-299 Parallelization of a Hierarchical Data Clustering Algorithm Using OpenMP