Участник:Kozlov Vladimir/Алгоритм Ланцоша для арифметики с плавающей точкой с полной переортогонализацией

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша — это итерационный алгоритм поиска $k$ приближённых собственных значений симметричной вещественной матрицы $A$ размера $n \times n$. Алгоритм применяется, когда матрица $A$ слишком велика, чтобы к ней можно было применять точные прямые методы вычисления собственных значений. Алгоритм метод Рэлея — Ритца поиска приближённых собственных значений и метод Ланцоша построения крыловского подпространства.

Метод Рэлея — Ритца является методом поиска $k$ приближённых собственных значений симметричной вещественной матрицы $A$ размера $n \times n$. Если $Q = [Q_k, Q_u]$ — ортонормированная матрица размера $n \times n$, $Q_k$ имеет размер $n \times k$, $Q_u$ имеет размер $n \times n - k$, то можно записать равенство

$T = Q^T A Q = [Q_k, Q_u]^T A [Q_k, Q_u] = \left[ \begin{array}{cc} Q_k^T A Q_k & Q_k^T A Q_u\\ Q_u^T A Q_k & Q_u^T A Q_u \end{array} \right] = \left[ \begin{array}{cc} T_{k} & T_{ku}^T\\ T_{ku} & T_{u} \end{array} \right].$

Метод Рэлея — Ритца заключается в том, что собственные значения матрицы $T_k = Q_k^T A Q_k$ объявляются приближёнными собственными значениями матрицы $A$. Такое приближение является в некотором смысле «наилучшим»: можно показать, что если $T_k = V \Lambda V^{-1}$ — спектральное разложение $T_k$, то пара $(Q_k V, \Lambda)$ минимизирует функционал $L(P_k, D) = \Vert A P_k - P_k D \Vert_2$, причём $L(Q_k V, \Lambda) = \Vert T_{ku} \Vert_2$, то есть $A \approx (Q_k V) \Lambda (Q_k V)^{-1}$. Из этого также видно, что метод Рэлея — Ритца позволяет получать приближения для собственных векторов матрицы $A$. Более того, можно показать, что собственные значения $T$ отличаются от некоторых собственных значений $A$ не более чем на $\Vert T_{ku} \Vert_2$.

Метод Ланцоша — это метод построения матрицы $Q$, при использовании которого, во-первых, матрица $T$ оказывается симметричной трёхдиагональной, во-вторых, столбцы $Q$ и $T$ вычисляются последовательно. Трёхдиагональность $T$ приводит к следующим явлениям:

1. матрица $T_k$ является трёхдиагональной матрицей меньшей размерности, а для трёхдиагональных матриц существуют высокоэффективные методы поиска собственных значений;
2. матрица $T_{ku}$ имеет только один ненулевой (возможно) элемент — правый верхний, а значит, для оценки погрешности полученных собственных значений достаточно знать только этот элемент.

В теории в методе Ланцоша для вычисления каждого следующего столбца $q_{j + 1}$ матрицы $Q$ достаточно знать только $q_{j - 1}$ и $q_{j}$ в силу трёхдиагональности матрицы $T$. На практике из-за ошибок округления, если не предпринимать специальных мер, набор векторов $q_{1}, \dots, q_{k}$ перестаёт быть ортогональным. Для борьбы с этим явлением на каждом шаге метода Ланцоша приходится выполнять так называемую переортогонализацию — повторно запускать процесс ортогонализации Грама — Шмидта.

1.2 Математическое описание алгоритма

Исходные данные: симметричная вещественная матрица $A$ — матрица, для которой будут вычисляться собственные значения, вектор $b$ — начальное приближение для метода Ланцоша.

Выходные данные: трёхдиагональная симметричная вещественная матрица $T_k = \left[ \begin{array}{cccc} \alpha_1 & \beta_1 & & \\ \beta_1 & \ddots & \ddots & \\ & \ddots & \ddots & \beta_{k - 1}\\ & & \beta_{k - 1} & \alpha_k \end{array} \right]$, ортонормированный набор векторов $q_1, \dots, q_k$: $T_k = [q_1, \dots, q_k]^T A [q_1, \dots, q_k]$.

Формулы метода:

$\begin{array}{l} q_1 = b / \Vert b \Vert_2\\ j = \overline{1, k}:\\ \quad z_j = A q_j \\ \quad \alpha_j = q_j^T A q_j = q_j^T z_j \\ \quad z_j' = z_j - \sum_{i=1}^j (z_j^T q_i) q_i \\ \quad z_j'' = z_j' - \sum_{i=1}^j (z_j'^T q_i) q_i\\ \quad \beta_j = \Vert z_j'' \Vert_2\\ \quad q_{j+1} = z_j'' / \Vert z_j'' \Vert_2 = z_j''/\beta_j \end{array}$

Собственные значения и собственные векторы матрицы $T_k$ ищутся любым прямым алгоритмом.

Вычисление $z_j', z_j''$ — это полная переортогонализация $z_j$ методом Грама — Шмидта. Двойной запуск практически гарантирует, что $z_j''$ будет ортогонален $q_1, \dots, q_j$. Заметим, что $\sum_{i=1}^j (z^T q_i) q_i = Q_j Q_j^T z$, где $Q_j = [q_1, \dots, q_j]$, поэтому переортогонализацию можно переписать в виде $z'_j = z_j - Q_j Q_j^T z_j, z_j'' = z_j' - Q_j Q_j^T z_j'$.

Если $\beta_j = 0$ для какого-либо $j \lt k$, то $\Vert T_{ju}\Vert_2 = 0$, а значит, собственные значения $T_j$ в точности совпадают с каким-то собственными значениями $A$. В этом случае дальнейшие вычисления прекращаются и либо используется полученная $T_j$ размерности меньшей, чем $k$, либо процедура запускается заново с другим начальным вектором $b$.

1.3 Вычислительное ядро алгоритма

У алгоритма построения матрицы $T_k$ в том виде, как он описан выше, можно выделить два ядра:

1. умножение матрицы $A$ на вектор $q_j$: $z_j = A q_j$ ($O(n^2)$ умножений вещественных чисел);
2. переортогонализация: $z'_j = z_j - Q_j Q_j^T z_j,\; z_j'' = z_j' - Q_j Q_j^T z_j'$ ($O(nk^2)$ умножений вещественных чисел).

1.4 Макроструктура алгоритма

Для реализации алгоритма по указанным выше формулам имеет смысл выделить следующие макрооперации:

• арифметические операции над матрицами и векторами (сложение и умножение на число);
• умножение матрицы на вектор и скалярное произведение векторов;
• вычисление нормы вектора;
• добавление к матрице столбца.

1.5 Схема реализации последовательного алгоритма

$\begin{array}{l} \mathtt{input:}\; A, b, k\\ q_1 = b / \Vert b \Vert_2\\ Q = q_1\\ \mathtt{for}\; j = \overline{1, k}:\\ \quad z = A q_j \\ \quad \alpha_j = q_j^T z \\ \quad z = z - Q \left( Q^T z \right) \\ \quad z = z - Q \left( Q^T z \right)\\ \quad \beta_j = \Vert z \Vert_2\\ \quad \mathtt{if }\; \beta_j = 0\\ \quad \quad \mathtt{exit}\\ \quad \mathtt{end \; if}\\ \quad q_{j+1} = z/\beta_j\\ \quad Q = [Q, q_{j + 1}]\\ \mathtt{end \; for}\\ \mathtt{output:}\; [\alpha_1, \dots, \alpha_k], [\beta_1, \dots, \beta_{k - 1}], [q_1, \dots, q_k]. \end{array}$

Следует заметить, что очень часто в макрооперациях возникает операция вычисления суммы всех элементов массива. Её необходимо выполнять и при умножении матрицы на вектор, и при вычислении скалярного произведения, и при вычислении нормы вектора. Разные методы суммирования дают разный ресурс параллелизма. В этой работе предполагается, что везде для суммирования используется последовательный способ.

1.6 Последовательная сложность алгоритма

На $j$-ой итерации алгоритм выполняет

• $n^2 + n + 4nj + n + n = n^2 + 3n + 4nj$ умножений и делений;
• $n(n - 1) + (n - 1) + (4n - 2)j + (n - 1) = n^2 + (n - 2) + (4n - 2)j$ сложений и вычитаний;
• одно извлечение квадратного корня.

Всего за $k$ итераций алгоритм выполняет

• $(n + 3)nk + 2nk(k + 1)$ умножений и делений;
• $(n^2 + n - 2)k + (2n - 1)k(k + 1)$ сложений и вычитаний.

Таким образом, алгоритм имеет последовательную сложность $O(n^2k) + O(nk^2)$.

1.7 Информационный граф

Рисунок 1. Информационный граф алгоритма Ланцоша на уровне итераций с входными и выходными данными. In — входные данные (матрица $A$ и вектор $b$), Out — выходные данные ($\alpha_j, \beta_j$ и $q_j$), nrm — вычисление еклидовой нормы вектора, / — деление вектора на число, Iter — итерации алгоритма.

Рисунок 2. Информационный граф итерации алгоритма Ланцоша на уровне макроопераций. In — входные данные (матрица $A$), Out — выходные данные ($\alpha_j, \beta_j$ и $q_j$), dprod — скалярное произведение векторов, mprod — произведение матрицы на вектор, - — разность векторов, nrm — вычисление еклидовой нормы вектора, / — деление вектора на число.

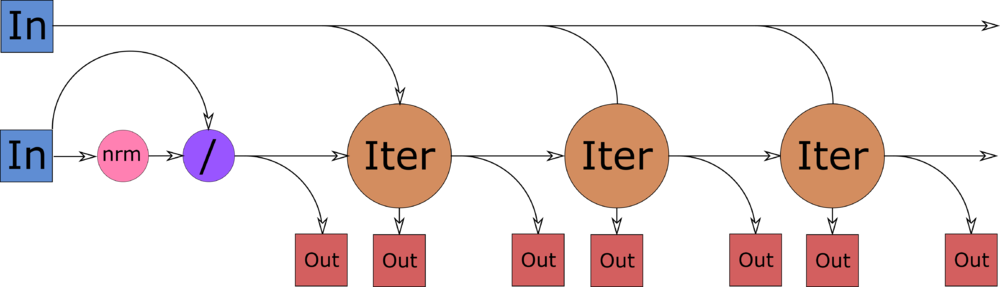
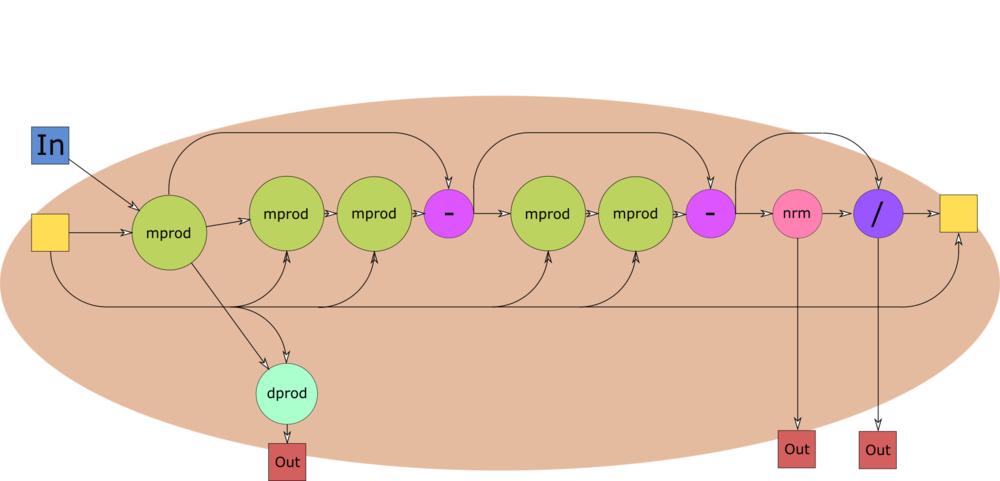
1.8 Ресурс параллелизма алгоритма

Для реализации $j$-ой итерации алгоритма нужно выполнить следующие ярусы:

1. $n$ ярусов сложений с $n$ операциями умножения в каждом (вычисление $z$);
2. $n$ ярусов сложений с $1$ операцией умножения в каждом (вычисление $\alpha_j$);
3. $j$ ярусов сложений с $n$ операциями умножения в каждом, $n$ ярусов сложений с $j$ операциями умножения в каждом, $1$ ярус вычитаний размера $n$ (первая переортогонализация);
4. $j$ ярусов сложений с $n$ операциями умножения в каждом, $n$ ярусов сложений с $j$ операциями умножения в каждом, $1$ ярус вычитаний размера $n$ (вторая переортогонализация);
5. $n$ ярусов сложений с $1$ операцией умножения в каждом (вычисление $\beta_j$);
6. $1$ ярус делений размера $n$ (вычисление $q_{j + 1}$).

Итого ширина ЯПФ одной итерации составляет $O(n)$, высота — $4n + 2j + 3$. Ширина ЯПФ всего алгоритма составляет $O(n)$, высота — $O(nk) + O(k^2)$.

1.9 Входные и выходные данные алгоритма

Входные данные: вещественная симметричная матрица $A$, вектор $b$, число $k$.

Размер входных данных: $n^2 + n$.

Выходные данные: набор чисел $\alpha_1, \dots, \alpha_k, \beta_1, \dots, \beta_{k - 1}$, набор векторов $q_1, \dots, q_k$.

Размер выходных данных: $2k - 1 + nk$.

1.10 Свойства алгоритма

• Алгоритм недетерминирован, так как он может досрочно завершить работу.
• Алгоритм устойчив благодаря операции переортогонализации.
• Соотношение последовательной и параллельной сложности алгоритма — $n$. Распараллелирование позволяет сделать алгоритм из квадратичного по $n$ линейным по $n$.
• Вычислительная мощность — порядка $2k$.
• В алгоритме есть длинные дуги — на протяжение всех итераций необходимо хранить набор векторов $Q$.