Участник:Nikita270a: различия между версиями
| Строка 9: | Строка 9: | ||
| − | Авторы: | + | Авторы: Алексейчук Н.Н 616, Ястребов К.С. 609. |
== Общее описание алгоритма. == | == Общее описание алгоритма. == | ||
| Строка 30: | Строка 30: | ||
<math> K_m(v,A) = span[x_1, Ax_1, A^2x_1, ..., A^{k-1}x_1] </math> | <math> K_m(v,A) = span[x_1, Ax_1, A^2x_1, ..., A^{k-1}x_1] </math> | ||
| − | В качестве входных данных для алгоритма Ланцоша подаются квадратная матрица размерности <math>n</math>X<math>n</math>: <math>A=A^T</math>; а так же вектор начального приближения <math>b</math>. | + | В качестве входных данных для алгоритма Ланцоша подаются квадратная матрица размерности <math>n</math>X<math>n</math>: <math>A=A^T</math>; а так же вектор начального приближения <math>b</math>. |
| + | Метод осуществляет поиск трехдиагональной симметричной матрицы <math>T_k=Q_k^TAQ_k</math>. Причем собственные значения <math>T_k</math> таковы, что приближают собственные значения исходной матрицы <math>A</math>. То есть на каждом <math>k</math>-м шаге из ортонормированных векторов Ланцоша строится матрица <math>Q_k = [q_1,q_2,...,q_k]</math> и в качестве приближенных собственных значений матрицы <math>A</math> принимаются числа Ритца. | ||
| + | |||
| + | == Вычислительное ядро алгоритма == | ||
| + | |||
| + | Вычислительным ядром данного алгоритма являются следующие шаги: | ||
| + | *1. <math>Aq=( \sum\nolimits_{i=^n}a_{1i}q_i, \sum\nolimits_{i=2}^na_{2i}q_i, ..., \sum\nolimits_{i=1}^na_{ni}q_i)</math>. | ||
| + | |||
| + | *2. <math>z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i.</math> | ||
| + | |||
| + | В данном случае первая операция выполняет умножение симметричной матрицы <math>A</math> размерности <math>n</math>X<math>n</math> на <math>n</math>-мерный вектор <math>q</math>, вследствие чего вычислительная сложность выполнения заключается в <math>n^2</math> умножений и <math>n^2-n</math> сложений. Второе действие является процессом ортогонализации Грама-Шмидта. В последнем действии вычисляются <math>k^2n+k(n+2)</math> умножений и <math>k^2n + k(n + 1) + 2</math> операций сложения. | ||
== Схема == | == Схема == | ||
| Строка 55: | Строка 65: | ||
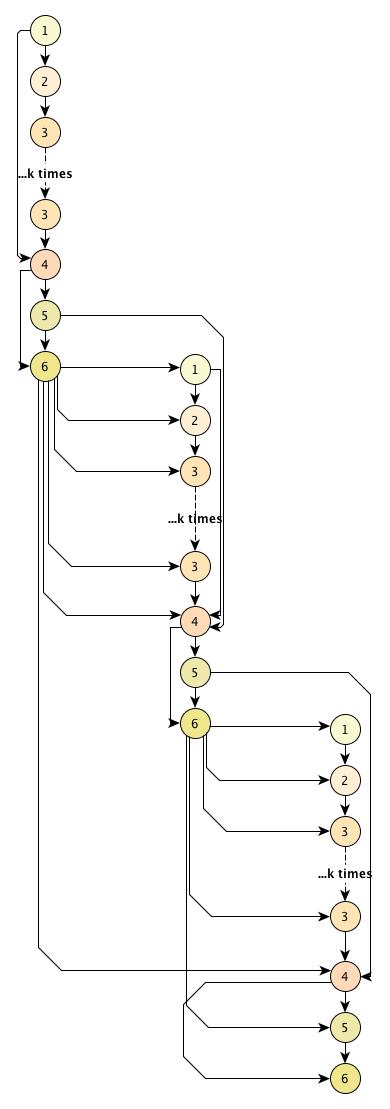
== Информационный граф == | == Информационный граф == | ||
| − | + | [[Файл:Graph.jpg]] | |
== Библиотеки реализующие алгоритм== | == Библиотеки реализующие алгоритм== | ||
Версия 00:20, 17 октября 2016
| Алгоритм Ланцоша с полной переортогонализацией | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n^2)[/math] |
| Объём входных данных | [math]\frac{n(n + 1)}{2}[/math] |
| Объём выходных данных | [math]k(n + 1)[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(k)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n^2)[/math] |
Авторы: Алексейчук Н.Н 616, Ястребов К.С. 609.
Содержание
1 Общее описание алгоритма.
Алгоритм Ланцоша ищет собвственные значения и собственные векторы для симетричной матрицы A вещественных чисел. Является итерацонным алгоритмом. Алгоритм Ланцоша использует степенной метод ([math] b_{k+1} = \frac{Ab_k}{||Ab_k||} [/math]) для поиска наибольших собственных значений и векторов матриц.
В отличие от прямых алгоритмов требует мешьше памяти и мощности, что является несомненным плюсом для больших матриц.
Несмотря на свою скорость работы и экономию памяти, сначала не был популярным алгоритмом из – за недостаточной вычислительной устойчивости. В 1970 году Ojalvo и Newman показали способ сделать алгоритм достаточно устойчивым. В этой же статье алгоритм был применен к расчету инженерной конструкции с большим количеством узлов, которые подвергались динамической нагрузке.
2 Математическое описание алгоритма
Памятка: Степенной метод нахождения наибольшего собственного числа матрицы можно сформулировать в предельном виде: если [math] b_0 [/math] – случайный вектор, и [math] b_n+1 = Ab_n [/math], тогда для больших чисел n предел [math]x_n/||x_n|| [/math] стремится к нормированному наибольшему собственному вектору.
Алгоритм Ланцоша комбинирует метод Ланцоша для нахождения крыловского подпространства и метод Релэя – Ритца.
Подпространство Крылова для степенного метода: [math] K_m(v,A) = span[x_1, Ax_1, A^2x_1, ..., A^{k-1}x_1] [/math]
В качестве входных данных для алгоритма Ланцоша подаются квадратная матрица размерности [math]n[/math]X[math]n[/math]: [math]A=A^T[/math]; а так же вектор начального приближения [math]b[/math].
Метод осуществляет поиск трехдиагональной симметричной матрицы [math]T_k=Q_k^TAQ_k[/math]. Причем собственные значения [math]T_k[/math] таковы, что приближают собственные значения исходной матрицы [math]A[/math]. То есть на каждом [math]k[/math]-м шаге из ортонормированных векторов Ланцоша строится матрица [math]Q_k = [q_1,q_2,...,q_k][/math] и в качестве приближенных собственных значений матрицы [math]A[/math] принимаются числа Ритца.
3 Вычислительное ядро алгоритма
Вычислительным ядром данного алгоритма являются следующие шаги:
- 1. [math]Aq=( \sum\nolimits_{i=^n}a_{1i}q_i, \sum\nolimits_{i=2}^na_{2i}q_i, ..., \sum\nolimits_{i=1}^na_{ni}q_i)[/math].
- 2. [math]z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i.[/math]
В данном случае первая операция выполняет умножение симметричной матрицы [math]A[/math] размерности [math]n[/math]X[math]n[/math] на [math]n[/math]-мерный вектор [math]q[/math], вследствие чего вычислительная сложность выполнения заключается в [math]n^2[/math] умножений и [math]n^2-n[/math] сложений. Второе действие является процессом ортогонализации Грама-Шмидта. В последнем действии вычисляются [math]k^2n+k(n+2)[/math] умножений и [math]k^2n + k(n + 1) + 2[/math] операций сложения.
4 Схема
Input: A, b (random vector with unit norm)
- [math] \begin{align} q_1 = b/||b||_2, \beta_0 = 0, q_0 = 0 \\ for j = 1 ,...,k \\ q_1&=b/||b||,\beta_0=0,q_o=0. \\ z&=Aq_j, \\ \alpha_j&=q_j^Tz, \\ z&=z-\alpha_jq_j-\beta_{j-1}q_{j-1}, \\ \beta&=||z||,\\ q_{j+1}&=z/\beta_j, \quad j \in [1, k]. \end{align} [/math]
5 Информационный граф
6 Библиотеки реализующие алгоритм
The IETL Project http://www.comp-phys.org/software/ietl/ C++
NAG Library http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R
ARPACK https://people.sc.fsu.edu/~jburkardt/m_src/arpack/arpack.html MATLAB
GrapLab https://turi.com/products/create/open_source.html C++
С частично переортаганализацией
LANSO/PLANSO http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran (уже распараллелена)