Участник:Alexander34396/Обобщенный метод минимальных невязок: различия между версиями
Kpetrov (обсуждение | вклад) |
Kpetrov (обсуждение | вклад) |
||
| Строка 135: | Строка 135: | ||
:a) Вычисление этой формулы требует <math> nm </math> мультипликативных операций. | :a) Вычисление этой формулы требует <math> nm </math> мультипликативных операций. | ||
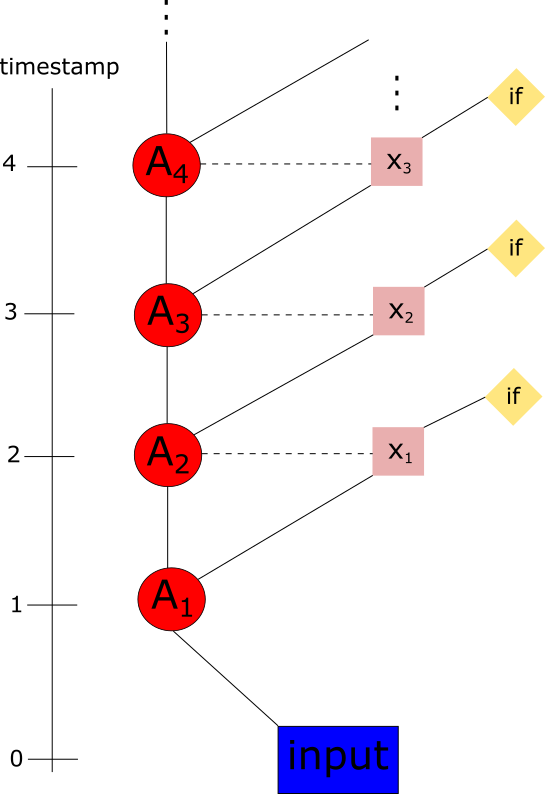
| − | + | [[File: Drawing.png]] | |
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
Версия 01:27, 18 октября 2016
 | Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 18.10.2016 Авторы этой статьи считают, что задание выполнено. |
Основные авторы описания: А.А.Ульянов (разделы 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.9, 2.7), К.Петров (разделы 1.7, 1.8, 1.10, 2.4).
| Обобщенный метод минимальных невязок | |
| Последовательный алгоритм | |
| Последовательная сложность | O(nm^2) |
| Объём входных данных | (n + 1)^2 |
| Объём выходных данных | n |
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Ресурс параллелизма алгоритма
- 1.8 Входные и выходные данные алгоритма
- 1.9 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Обобщённый метод минимальных невязок (англ. Generalized minimal residual method, GMRES) - итерационный метод численного решения системы линейных алгебраических уравнений с невырожденной матрицей. Метод основан на минимизации квадратичного функционала невязки на подпространствах Крылова. Разработан Юсефом Саадом и Мартином Шульцем[1] в 1986 году как обобщение метода MINRES[2] на случай систем с несимметричными матрицами.
1.2 Математическое описание алгоритма
Исходные данные:
- система линейных алгебраических уравнений вида Ax = b , где A — невырожденная матрица размера n-на- n ;
- x_0 - начальное приближение.
Вычисляемые данные:
- x_k - приближённое решение исходной системы.
Метод GMRES приближает точное решение исходной системы Ax = b вектором x_k , который минимизирует l_2 -норму невязки r_k = Ax_k - b на подпространстве Крылова:
- K_k = K_k(A,b) = \operatorname{span} \, \{ b, Ab, A^2b, \ldots, A^{k-1}b \} .
На каждой итерации метода решение уточняется поправкой, представленной в виде разложения по l_2 -ортонормированному базису пространства K_k :
- x_k = x_0 + z_k , где x_0 - некоторое начальное приближение, z_k \in K_k - поправка решения.
1.2.1 Ортогонализация Арнольди
Для построения ортонормированного базиса K_k метод использует процесс Арнольди.
Исходные данные:
- v_1 , такой что \|v_1\|_2 = 1 ;
- матрица A размером n -на- n .
Формула процесса:
- h_{j+1j}v_{j+1} = Av_j - \sum_{i=1}^j h_{ij}v_{j} , где h_{ij} = (Av_j, v_i), \quad j=1,\ldots,k .
Алгоритм процесса:
Выполнять для \quad j=1,\ldots,k :
- h_{ij} = (Av_j, v_i), \quad i=1,\ldots,j ;
- \hat{v}_{j+1} = Av_j - \sum_{i=1}^j h_{ij}v_{i} ;
- h_{j+1j} = \|\hat{v}_{j+1}\|_2 ;
- v_{j+1} = \frac{\hat{v}_{j+1}}{h_{j+1j}} .
При введении матричных обозначений можно записать:
- z_k = V_ky_k , где y_k \in \mathbb{R}^k - вектор коэффициентов;
- AV_k = V_kH_k + h_{k+1k}v_{k+1} e_k^T = V_{k+1}\overline{H}_k , где V_k = [v_1|v_2|...|v_k] , а \overline{H}_k - верхняя матрица Хессенберга размерности (j+1) на j .
1.2.2 Минимизация функционала невязки
Для решения исходной системы GMRES вычисляет приближённое решение x_k , которое минимизизует функционал невязки:
- J(y) = \|b- A x_k\|_2 = \|b - A(x_0 + V_ky)\|_2 = \|\beta e_1 - \overline{H}_ky_k \|_2 , где \beta = \|r_0\|_2 .
Вектор y_k может найден как решение линейной задачи наименьших квадратов размера k+1 -на- k :
- y_k = \arg\min_{y}\| \beta e_1 - \overline{H}_ky\|_2 .
Для решения задачи матрица \overline{H}_k приводится к верхнему треугольному виду с помощью k последовательных вращений Гивенса.
1.2.3 Общая схема метода
В общем виде k-aя итерация алгоритма GMRES может быть записан следующим образом:
- найти ортонормированный базис V_k подпространства K_k с помощью ортогонализации Арнольди;
- найти y_k , минимизирующий \|r_k\|_2 ;
- вычислить x_k = x_0 + V_ky_k , где x_0 - начальное приближение;
- вычислить r_k и остановиться,если требуемая точность была достигнута, иначе повторить.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро последовательной версии метода GMRES состоит из двух частей:
- Вычисление ортонормированного базиса K_k ;
- Формирование приближенного решения x_k .
Для вычисления ортонормированного базиса K_k метод использует процесс Арнольди:
- h_{j+1j}v_{j+1} = Av_j - \sum_{i=1}^j h_{ij}v_{j} , где h_{ij} = (Av_j, v_i), \quad j=1,\ldots,k .
Для нахождения приближённого решения x_k метод использует формулу:
- x_k = x_0 + V_ky_k .
1.4 Макроструктура алгоритма
В алгоритме можно выделить следующие макрооперации:
- Умножение матрицы на вектор;
- Вычисление скалярного произведения векторов;
- Вычисление l_2 -нормы вектора;
- Умножение вектора на скаляр;
- Деление вектора на скаляр.
1.5 Схема реализации последовательного алгоритма
На практике используется перезапускаемая версия метода - GMRES(m):
1 Подготовка перед итерационным процессом:
- 1.1 Выбрать начальное приближение x_0 ;
- 1.2 Посчитать невязку r_0 = b - Ax_0 ;
- 1.3 Вычислить v_1 = \frac{r_0}{\|r_0\|_2} .
2 Построение ортонормированного базиса K_m :
- Для всех j от 1 до m по нарастанию выполнять:
- 2.1 h_{ij} := (Av_j, v_i), \quad i=1,\ldots,j ;
- 2.2 \hat{v}_{j+1} := Av_j - \sum_{i=1}^j h_{ij}v_{i} ;
- 2.3 h_{j+1j} = \|\hat{v}_{j+1}\|_2 ;
- 2.4 v_{j+1} = \frac{\hat{v}_{j+1}}{h_{j+1j}} .
3 Вычисление x_m :
- 3.1 x_m = x_0 + V_my_m , где y_m минимизирует \|r_0 - AV_my_m\|_2;
- 3.2 Вычислить r_m ;
- 3.3 Если требуемая точность достигнута, остановиться.
4 Перезапуск:
- 4.1 x_0 = x_m;
- 4.2 v_1 = \frac{r_m}{\|r_m\|_2};
- 4.3 Перейти к шагу 2.
1.6 Последовательная сложность алгоритма
Если пренебречь сложностью вычисления y_m , то общую сложность алгоритма GMRES можно разделить на две части:
1. Сложность вычисления ортонормированного базиса пространства K_m :
- a) Для вычисления j -го вектора базиса K_m, j \lt m требуется:
- NZ + (2j + 1)n мультипликативных операций, где NZ - количество ненулевых элементов матрицы A .
- b) Вычисление последнего вектора базиса требует:
- n(m + 1) мультипликативных операций.
- c) Общая мультипликативная сложность вычисления ортонормированного базиса K_m :
- O(nm^2) .
2. Сложность вычисления приближённого решения x_m :
- a) Вычисление этой формулы требует nm мультипликативных операций.
1.7 Ресурс параллелизма алгоритма
1.8 Входные и выходные данные алгоритма
Входные данные:
- A – квадратная матрица размера n -на- n ;
- b – вектор правой части размера n ;
- x_0 – начальное приближение размера n ;
- \epsilon – погрешность решения.
Для перезапускаемой версии алгоритма дополнительно:
- m – число итераций.
Объём входных данных: n^2 + 2n + 1 .
Выходные данные:
- x_k - вектор приближённого решения размера n .
Объём выходных данных: n .
1.9 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Реализации алгоритма GMRES присутствуют во многих программных пакетах:
3 Литература
<references \>
- ↑ Y.Saad, M.H. Schultz, GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems, SIAM J. Scientific and Stat. Comp. 7: 856-869 (1986)
- ↑ C. C. Paige and M. A. Saunders. Solution of sparse indefinite systems of linear equations, SIAM J. Numerical Analysis 12, 617-629 (1975)