Участник:KibAndrey/Ортогонализация Грама-Шмидта: различия между версиями
KibAndrey (обсуждение | вклад) |
KibAndrey (обсуждение | вклад) |
||
| Строка 22: | Строка 22: | ||
'''Процесс ортогонализации Грама–Шмидта'''<ref>Математическая энциклопедия / Гл. ред. | '''Процесс ортогонализации Грама–Шмидта'''<ref>Математическая энциклопедия / Гл. ред. | ||
| − | И. М. Виноградов — М: Советская энциклопедия — Т.4 Ок–Сло, 1984. — 215 с.</ref> — алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства <math>V</math> ортогональной системы ненулевых векторов | + | И. М. Виноградов — М: Советская энциклопедия — Т.4 Ок–Сло, 1984. — 215 с.</ref> — алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства <math>V</math> ортогональной системы ненулевых векторов, при котором каждый вектор построенной системы линейно выражается через векторы данной системы. |
| − | Исторически это первый алгоритм, описывающий процесс ортогониализации. Традиционно его связывают с именами [https://en.wikipedia.org/wiki/J%C3%B8rgen_Pedersen_Gram Йоргена Педерсена Грама] и [https://en.wikipedia.org/wiki/Erhard_Schmidt Эрхарда Шмидта]. Йорган Педерсен Грам<ref name="multiple">Meyer C. D. Matrix analysis and applied linear algebra. — Siam, 2000. — Т.2.</ref> был датским актуарием, который в неявном виде представил суть процесса ортогонализации в 1883 году. Нельзя не сказать о том, что метод ортогонализации в несколько ином, модифицированом виде, ранее использовал [https://en.wikipedia.org/wiki/Pierre-Simon_Laplace Пьер-Симон Лаплас] при нахождении массы Сатурна и Юпитера из систем нормальных уравнений и расчете распределения ошибок при этих вычислениях <ref> [https://books.google.ru/books?id=fjAVAAAAQAAJ&printsec=frontcover&hl=ru&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false Marquis de Laplace P. S. Théorie analytique des probabilités. ] — V. Courcier, 1820.</ref>. Ясно, что Й. Грам не знал о том, что Лаплас ранее использовал этот метод. Эрхард Шмидт<ref name="multiple">Meyer C. D. Matrix analysis and applied linear algebra. — Siam, 2000. — Т.2.</ref> был учеником великих математиков [https://en.wikipedia.org/wiki/Hermann_Schwarz Германа Шварца] и [https://en.wikipedia.org/wiki/David_Hilbert Давида Гильберта]. Алгоритм ортогонализации был опубликован Э. Шмидтом в 1907 году в его исследовании интегральных уравнений<ref name=Shmidt>Erchard Shmidt. Mathematische Annalen Zur Theorie der linearen und nichtlinearen Integralgleichungen, 1. Teil: Entwicklung willkürlicher | + | Исторически это первый алгоритм, описывающий процесс ортогониализации. Традиционно его связывают с именами [https://en.wikipedia.org/wiki/J%C3%B8rgen_Pedersen_Gram Йоргена Педерсена Грама] и [https://en.wikipedia.org/wiki/Erhard_Schmidt Эрхарда Шмидта]. Йорган Педерсен Грам<ref name="multiple">Meyer C. D. Matrix analysis and applied linear algebra. — Siam, 2000. — Т.2.</ref> был датским актуарием, который в неявном виде представил суть процесса ортогонализации в 1883 году. Нельзя не сказать о том, что метод ортогонализации в несколько ином, модифицированом виде, ранее использовал [https://en.wikipedia.org/wiki/Pierre-Simon_Laplace Пьер-Симон Лаплас] при нахождении массы Сатурна и Юпитера из систем нормальных уравнений и расчете распределения ошибок при этих вычислениях<ref> [https://books.google.ru/books?id=fjAVAAAAQAAJ&printsec=frontcover&hl=ru&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false Marquis de Laplace P. S. Théorie analytique des probabilités. ] — V. Courcier, 1820.</ref>. Ясно, что Й. Грам не знал о том, что Лаплас ранее использовал этот метод. Эрхард Шмидт<ref name="multiple">Meyer C. D. Matrix analysis and applied linear algebra. — Siam, 2000. — Т.2.</ref> был учеником великих математиков [https://en.wikipedia.org/wiki/Hermann_Schwarz Германа Шварца] и [https://en.wikipedia.org/wiki/David_Hilbert Давида Гильберта]. Алгоритм ортогонализации был опубликован Э. Шмидтом в 1907 году в его исследовании интегральных уравнений<ref name=Shmidt>Erchard Shmidt. Mathematische Annalen Zur Theorie der linearen und nichtlinearen Integralgleichungen, 1. Teil: Entwicklung willkürlicher |
Funktionen nach Systemen vorgeschriebener. – Mathematische Annalen, 63 (1907), pp. 433–476.</ref>, которое в свою очередь дало основание для развития теории гильбертовых пространств. Шмидт использовал процесс ортогонализации применительно к геометрии гильбертова пространства решений интегральных уравнений отмечал, что процесс ортогонализации принципиально такой же, какой прежде использовал Й. Грам. В отечественной литературе иногда этот процесс называют ''ортогонализацией Сонина–Шмидта''<ref>Краснов М.Л. Интегральные уравнения. Введение в теорию. — М.: Наука, 1975. — 302 с.</ref><ref>Марченко В.А. Введение в теорию обратных задач спектрального анализа. — Харьков: Акта, 2005. — 143 с.</ref>. Это название связано с тем, что разработанный Сониным<ref>О некоторых неравенствах, относящихся к определенным интегралам. Записки Академии наук по физико-математическому отделению. Серия 8. Т. 6 № 6. — C. 1–53.</ref> метод ортогонализации системы функций для частного случая по существу не отличается от метода ортогонализации системы функций, предложенного ранее Шмидтом<ref name=Shmidt>Erchard Shmidt. Mathematische Annalen Zur Theorie der linearen und nichtlinearen Integralgleichungen, 1. Teil: Entwicklung willkürlicher | Funktionen nach Systemen vorgeschriebener. – Mathematische Annalen, 63 (1907), pp. 433–476.</ref>, которое в свою очередь дало основание для развития теории гильбертовых пространств. Шмидт использовал процесс ортогонализации применительно к геометрии гильбертова пространства решений интегральных уравнений отмечал, что процесс ортогонализации принципиально такой же, какой прежде использовал Й. Грам. В отечественной литературе иногда этот процесс называют ''ортогонализацией Сонина–Шмидта''<ref>Краснов М.Л. Интегральные уравнения. Введение в теорию. — М.: Наука, 1975. — 302 с.</ref><ref>Марченко В.А. Введение в теорию обратных задач спектрального анализа. — Харьков: Акта, 2005. — 143 с.</ref>. Это название связано с тем, что разработанный Сониным<ref>О некоторых неравенствах, относящихся к определенным интегралам. Записки Академии наук по физико-математическому отделению. Серия 8. Т. 6 № 6. — C. 1–53.</ref> метод ортогонализации системы функций для частного случая по существу не отличается от метода ортогонализации системы функций, предложенного ранее Шмидтом<ref name=Shmidt>Erchard Shmidt. Mathematische Annalen Zur Theorie der linearen und nichtlinearen Integralgleichungen, 1. Teil: Entwicklung willkürlicher | ||
Funktionen nach Systemen vorgeschriebener. — Mathematische Annalen, 63 (1907), pp. 433–476.</ref>. | Funktionen nach Systemen vorgeschriebener. — Mathematische Annalen, 63 (1907), pp. 433–476.</ref>. | ||
Версия 19:15, 21 октября 2016
| Ортогонализация Грама-Шмидта | |
| Последовательный алгоритм | |
| Последовательная сложность | O\left(k^2n\right) |
| Объём входных данных | kn |
| Объём выходных данных | kn |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(k\log{n}) |
| Ширина ярусно-параллельной формы | O(kn) |
 | Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 21.10.2016 Авторы этой статьи считают, что задание выполнено. |
Основные авторы описания: А.В.Кибанов, Т.З.Аджиева. Все пункты данной статьи обсуждались и создавались совместно, доля ответственности равноправна.
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритма
1.1 Общее описание алгоритма
Процесс ортогонализации Грама–Шмидта[1] — алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства V ортогональной системы ненулевых векторов, при котором каждый вектор построенной системы линейно выражается через векторы данной системы.
Исторически это первый алгоритм, описывающий процесс ортогониализации. Традиционно его связывают с именами Йоргена Педерсена Грама и Эрхарда Шмидта. Йорган Педерсен Грам[2] был датским актуарием, который в неявном виде представил суть процесса ортогонализации в 1883 году. Нельзя не сказать о том, что метод ортогонализации в несколько ином, модифицированом виде, ранее использовал Пьер-Симон Лаплас при нахождении массы Сатурна и Юпитера из систем нормальных уравнений и расчете распределения ошибок при этих вычислениях[3]. Ясно, что Й. Грам не знал о том, что Лаплас ранее использовал этот метод. Эрхард Шмидт[2] был учеником великих математиков Германа Шварца и Давида Гильберта. Алгоритм ортогонализации был опубликован Э. Шмидтом в 1907 году в его исследовании интегральных уравнений[4], которое в свою очередь дало основание для развития теории гильбертовых пространств. Шмидт использовал процесс ортогонализации применительно к геометрии гильбертова пространства решений интегральных уравнений отмечал, что процесс ортогонализации принципиально такой же, какой прежде использовал Й. Грам. В отечественной литературе иногда этот процесс называют ортогонализацией Сонина–Шмидта[5][6]. Это название связано с тем, что разработанный Сониным[7] метод ортогонализации системы функций для частного случая по существу не отличается от метода ортогонализации системы функций, предложенного ранее Шмидтом[4].
1.2 Математическое описание алгоритма
Bходные данные: k линейно независимых векторов \mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a_k} длины n \left(\alpha_{ij}\right., j=1,2, \ldots,n, — координаты вектора \left.\mathbf{a_i}\right) .
Вычисляемые данные:
k ортогональных векторов \mathbf{b_1},\mathbf{b_2},...,\mathbf{b_k} длины n, причем \mathbf{b_1}=\mathbf{a_1}, либо
k ортонормированных векторов \mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k} длины n, причем \mathbf{q_i}=\frac{\mathbf{b_i}}{|\mathbf{b_i}|}, i=1,2, \ldots,k.
Формулы процесса ортогонализации:
- \begin{align} \mathbf{b_{1}} & =\mathbf{a_{1}}, \\ \mathbf{b_{2}}& =\mathbf{a_{2}}-\mathbf{b_{1}} proj_{\mathbf{b_1}}\mathbf{a_{2}}, \\ & ...\\ \mathbf{b_{i}} & =\mathbf{ a_{i}}-\sum\limits_{j=1}^{i-1}\mathbf{b_{i}} proj_{\mathbf{b_j}}\mathbf{a_{i}}.\\ & ...\\ \mathbf{b_{k}} & =\mathbf{ a_{k}}-\sum\limits_{j=1}^{k-1}\mathbf{b_{k}} proj_{\mathbf{b_j}}\mathbf{a_{k}}.\\ \end{align}
Здесь proj_{\mathbf{b_j}}\mathbf{a_{i}}, для j=1,...,i-1 — это число, равное по величине проекции вектора \mathbf{a_{j}} на ось, проходящую через вектор \mathbf{b_j}.
Формула для ее вычисления, полученная из определения скалярного произведения: proj_{\mathbf{b_j}}\mathbf{a_{i}}=\dfrac{(ai,bj)}{\mathbf{\left \|b_j\right \|}}, для j=1,...,i-1
Произведение длин \mathbf{|b_1|},\mathbf{|b_2|},\ldots ,\mathbf{|b_k|} равно объему параллелепипеда, построенного на векторах системы \left\{\mathbf{a_i}\right\}, i=1,2,\ldots ,k, как на ребрах.
Явное выражение векторов \mathbf{b_i} для i=1,...,k через \mathbf{a_1},\mathbf{a_2},...,\mathbf{a_k} дает формула
\mathbf{b_i}= \begin{vmatrix} (a_1,a_1) & \cdots & (a_1,a_i-1) &a_1 \\ (a_{2},a_1) & \cdots & (a_2,a_i-1) &a_2 \\ \cdots & \cdots & \cdots& \cdots \\ (a_{i},a_1) & \cdots & (a_i,a_i-1) &a_i \\ \end{vmatrix} . (В правой части этого равенства определитель следует формально разложить по последнему столбцу).
Иногда полученные векторы нормируются сразу после их нахождения и находится система ортонормированных векторов \mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k}. В этом случае знаменатель в формуле для вычисления проекции |\mathbf{q_i}|=1 для i=1,...,k-1, что существенно упрощает вычисления алгоритма. В настоящей статье применяя процесс ортогонализации к системе линейно независимых векторов, мы так и будем поступать.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит из вычисления:
- \dfrac{k(k+1)}{2} скалярных произведений векторов
(включая нахождения скалярных произведений одинаковых векторов дальнейшего нахождения их длин);
- \dfrac{(k-1)k}{2} умножений векторов на число после вычисления нового базисного вектора на итерации.
1.4 Макроструктура алгоритма
В уже отмечено описании вычислительного ядра алгоритма, основную часть метода составляют вычисления скалярных произведений, как для вычислении длины очередного вектора так и для расчета проекций прочих векторов на новый вектор, а также умножения векторов на числа, используемые при корректировке значений остальных векторов после вычисления очередного вектора, ортогонального предыдущим.
1.5 Схема реализации последовательного алгоритма
Входные данные: k линейно независимых векторов \mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a_k} длины n \left(\alpha_{ij}\right., где j=1,2, \ldots,n — координаты вектора \mathbf{a_i}, для \left.i=1,2, \ldots,k\right).
Вычисляемые данные:
k ортогональных векторов \mathbf{b_1},\mathbf{b_2},...,\mathbf{b_k} длины n \left(\beta_{ij}\right., где j=1,2, \ldots,n — координаты вектора \mathbf{b_i}, для \left.i=1,2, \ldots,k\right), причем \mathbf{b_1}=\mathbf{a_1}, либо
k ортонормированных векторов \mathbf{q_1},\mathbf{q_2},\ldots,\mathbf{q_k} длины n (\gamma_{ij}, j=1,2, \ldots,n — координаты вектора \mathbf{q_i}, для \left.i=1,2, \ldots,k\right), причем \mathbf{q_1}=\frac{\mathbf{b_i}}{|\mathbf{b_i}|}, для i=1,2, \ldots,k.
Последовательность исполнения метода:
1. len(a_1)=\sqrt{\alpha_{11}^2+\alpha_{12}^2+\ldots+\alpha_{1n}^2}.
2. При i от 1 до n:
- \gamma_{1j}= \frac{\alpha_{1j}}{len(a_1)}.
3. При i от 2 до k:
- при j от 1 до n:
- \beta_{ij}=\alpha_{ij}-\sum\limits_{k=1}^{j-1}\left(\sum\limits_{m=1}^n \alpha_{im}\gamma_{km}\right)\gamma_{kj}
- len(b_i)=\sqrt{\beta_{i1}^2+\beta_{i2}^2+\ldots+\beta_{in}^2}
- при j от 1 до n:
- \gamma_{ij}= \frac{\beta_{ij}}{len(b_{i})}.
- при j от 1 до n:
1.6 Последовательная сложность алгоритма
Для ортогонализации n линейно независимых векторов длины n в последовательном варианте с помощью классического метода ортогонализации Грама-Шмидта потребуется:
- k вычислений квадратного корня
- \frac{k(k-1)(n-1)}{2} сложений,
- \frac{k(k-1)(n-1)}{2} вычитаний,
- k^2 n умножений,
- k делений.
Умножения, сложения и вычитания составляют основную часть алгоритма.
При классификации по последовательной сложности, таким образом, метода ортогонализации Грама-Шмидта с кубической сложностью.
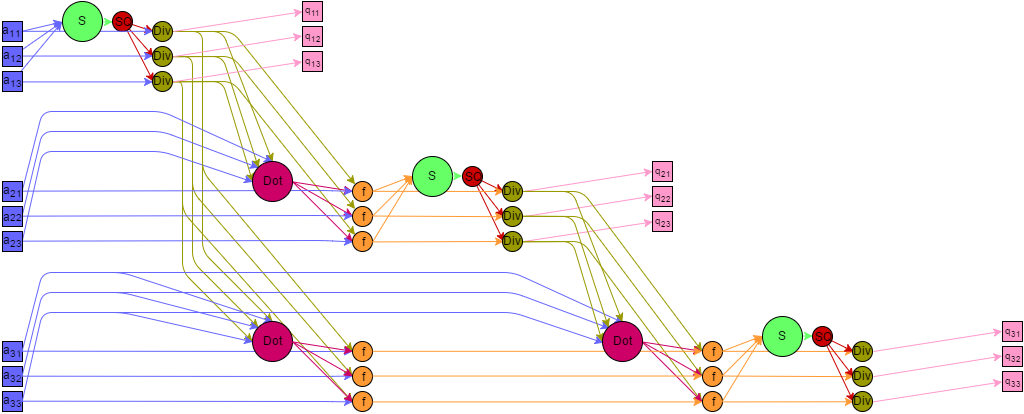
1.7 Информационный граф
Представим граф алгоритма с помощью текстового описания, а также с помощью изображения.
Все вершины графа можно разбить на шесть групп, каждой из которых соответствует вид исполняемой операции. Каждая вершина расположена в точках с целочисленными координатами, в пространствах с числом измерений от 1 до 4. Дадим описание каждой из групп.
Первая группа — вершины, которым соответствует операция возведение в квадрат. На графе они располагаются в двумерной области. i изменяется от 1 до k, p изменяется от 1 до n.
Значениями аргументов для этих функций являются:
- при i = 1 — входные данные a_{1p};
- при i \gt 1 — результат выполнения функции в вершине шестой группы с координатами i-1,1,\mathbf{p}.
Результат этих операций является промежуточным данным алгоритма.
Вторая группа — вершины соответствующие операции сложения, которые проще разбить на две подгруппы, соответствующие четным и нечетным индексам. Они располагаются в четырехмерной области, i изменяется от 1 до 2k-1, j равно 1 для нечетных i и изменяется от 2 до k+1-\left\lceil{\dfrac{i}{2}}\right\rceil для четных i, p изменяется от 1 до \left\lceil{\dfrac{n}{2^{i}}}\right\rceil, t изменяется от 1 до T = \left\lceil{\log_{2}(p)}\right\rceil.
Значениями аргументов для этих функций являются:
- при j = 1, t = 1 — результат выполнения функций в вершинах первой группы с координатами (i+1)/2,1,2p и (i+1)/2,1,2p - 1;
- при j \gt 1, t = 1 — результат выполнения функции в вершинах пятой группы с координатами i/2,j-1,2p и i,j-1,2p - 1;
- при t \gt 1 — результат выполнения функций в вершинах второй группы с координатами i,j,2p,t-1 и i,j,2p-1,t-1 (это точно верно для случаев p являющихся степенью двойки. Для остальных вариантов аргументом может являться результат выполнения функций в вершинах второй группы с последней координатой меньшей чем t-1).
Результат этих операций является промежуточным данным алгоритма.
Третья группа — вершины, которым соответствует операция SQRT извлечения квадратного корня. Они расположены в одномерной области, i изменяется от 1 до k. Значением аргумента для этих функций является результат выполнения функции в вершине второй группы, с координатами i,1,1,T
Результат является промежуточным данным алгоритма
Четвертая группа – вершины, которым соответствует операция деления. Располагаются в двумерной области, i изменяется от 1 до k, p изменяется от 1 до n. Значениями аргументов для этих функций являются:
- делимое:
- при i = 1 — входные данные a_{1p};
- при i \gt 1 — результат выполнения функции в вершине шестой группы с координатами i-1,1,p;
- делитель - результат выполнения функции в вершине третьей группы с координатой i
Результат является выходным данным алгоритма q_{ip}
Пятая группа — вершины, которым соответствует операция a*b. Располагаются в трехмерной области, i изменяется от 1 до k-1, j изменяется от 1 до k-i, p изменяется от 1 до n. Значениями аргументов для этих функций являются:
- a:
- при i = 1 — входные данные a_{1+j,p};
- при i \gt 1 — результат выполнения функции в вершине шестой группы с координатами i-1,j+1,p;
- b — результат выполнения функции в вершине четвертой группы с координатой i
Результат является промежуточным данным алгоритма
Шестая группа – вершины которые соответствуют операции a - b*c. Располагаются в трехмерной области, i изменяется от 1 до k-1, j изменяется от 1 до k-i, p изменяется от 1 до n. Значениями аргументов для этих функций являются:
- a:
- при i = 1 — входные данные a_{1+j,p};
- при i \gt 1 — результат выполнения функции в вершине шестой группы с координатами i-1,j+1,p;
- b — результат выполнения функции в вершине второй группы, с координатами i,j+1,1,T
- c — результат выполнения функции в вершине четвертой группы с координатой i
Результат является промежуточным данным алгоритма.
Описанный граф для случая k = 3, n = 4 изображен на рисунке. Каждая группа вершин отличается цветом и буквенным обозначением. "S" — первая группа, "+" — вторая группа, "SQ" — третья группа, "Div" — четвертая группа, "M" — пятая группа, "f" — шестая группа. Квадратные метки "In" и "out" обозначают передачу входных и выходных данных соответственно.
1.8 Ресурс параллелизма алгоритма
Для построения ортонормированного базиса методом Грама–Шмидта необходимо выполнить следующие ярусы операций:
- k ярусов вычисления квадратов числа (по n операций на каждом);
- (2k-1)\left(\left\lceil{\log_{2}(n)}\right\rceil\right) ярусов суммирования (от 1 до \;(k-1)\cdot\dfrac{n}{2}\; операций на каждом);
- k ярусов вычисления квадратного корня (по одной операции на каждом);
- k ярусов деления( по k операций на каждом);
- k-1 ярус умножения пары чисел (от n до (k-1)n операций на каждом);
- k-1 ярус умножения/вычитания чисел (от n до (k-1)n операций на каждом).
В этом случае сложность алгоритма при классификации по высоте ЯПФ — O(k\log{n}), при классификации по ширине ЯПФ — O(kn).
1.9 Входные и выходные данные алгоритма
Входные данные: матрица A с элементами \alpha_{ij}, где i принимает значения 1,\ldots,k, j принимает значения 1,\ldots,n. Здесь k\leqslant n. По строкам этой матрицы записаны k линейно-независимых векторов некоторого пространства размерности n.
Объем входных данных: kn.
Выходные данные: матрица Q с элементами \gamma_{ij}. Строки этой матрицы также задают k векторов единичной длины размерности n, причем всякое скалярное произведение двух различных векторов этой системы равно 0.
Объем выходных данных: kn.
Замечание: Алгоритм может работать с вырожденной матрицей, он выдаёт нулевую строку на шаге j, если строка j матрицы A является линейной комбинацией предыдущих строк. В этом случае для корректного продолжения работы алгоритма необходима дополнительная проверка на равенство строки нулю и пропуск соответствующих строк. Количество построенных векторов будет равняться размерности пространства, порождаемого строками матрицы.
1.10 Свойства алгоритма
Отношение последовательной и параллельной сложности алгоритма в случае неограниченных ресурсов равно \dfrac{k^2n}{k\log{n}}=\dfrac{kn}{\log{n}}. Вычислительная мощность алгоритма линейная.
Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления.
Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов.
Большинство дуг информационного графа являются локальными. Исключение составляют дуги исходящие из операций деления и извлечения корня — для первой группы количество дуг пропорционально квадрату количества векторов, а для второй — пропорционально размерности пространства, в котором заданы эти вектора. Возникающие при это длинные дуги могут быть заменены несколькими короткими пересылками между соседями.
2 ЧАСТЬ Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Срок сдачи продлён до 15-го ноября.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Для классического метода ортогонализации Грама–Шмидта существуют реализации в математических программных пакетах, таких как Matlab, Maxima, Mathematica. Также метод реализован в библиотеке SpectralPython для языка Python. Для устранения проблемы ошибок численных округлений иногда используется повторное применение метода к уже построенному ортогональному базису.
Поскольку метод ортогонализации Грама–Шмидта гарантирует получение j ортогональных векторов к концу шага j, а не в самом конце работы алгоритма, используется в итерационных методах, таких как метод Арнольди. Для поддержки работы этого метода реализация ортогонализации Грама-Шмидта включена в библиотеку ARPACK.
3 Литература
- ↑ Математическая энциклопедия / Гл. ред. И. М. Виноградов — М: Советская энциклопедия — Т.4 Ок–Сло, 1984. — 215 с.
- ↑ Перейти обратно: 2,0 2,1 Meyer C. D. Matrix analysis and applied linear algebra. — Siam, 2000. — Т.2.
- ↑ Marquis de Laplace P. S. Théorie analytique des probabilités. — V. Courcier, 1820.
- ↑ Перейти обратно: 4,0 4,1 Erchard Shmidt. Mathematische Annalen Zur Theorie der linearen und nichtlinearen Integralgleichungen, 1. Teil: Entwicklung willkürlicher
Funktionen nach Systemen vorgeschriebener. – Mathematische Annalen, 63 (1907), pp. 433–476. Ошибка цитирования Неверный тег
<ref>: название «Shmidt» определено несколько раз для различного содержимого - ↑ Краснов М.Л. Интегральные уравнения. Введение в теорию. — М.: Наука, 1975. — 302 с.
- ↑ Марченко В.А. Введение в теорию обратных задач спектрального анализа. — Харьков: Акта, 2005. — 143 с.
- ↑ О некоторых неравенствах, относящихся к определенным интегралам. Записки Академии наук по физико-математическому отделению. Серия 8. Т. 6 № 6. — C. 1–53.