Участник:LKruglov/Алгоритм устойчивой кластеризации с использованием связей

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 28.10.2016 Авторы этой статьи считают, что задание выполнено.

Алгоритм устойчивой кластеризации с использованием связей
Последовательный алгоритм
Последовательная сложность	[math]O(n^{2,37} + n^2\log n)[/math], если для вычисления количества связей используется алгоритм Копперсмита—Винограда
Объём входных данных	Вектор из [math]n[/math] точек в виде векторов характеристик произвольного вида, дополнительно одно вещественное и одно челое число [math]k[/math]
Объём выходных данных	Сгруппированные в [math]k[/math] кластеров [math]n[/math] классифицируемых точек представленных индексами во входном векторе

Авторы: Круглов Л. В.(1.1,1.2,1.3,1.6,1.8,1.10), Баранов М. С.(1.1,1.2,1.3,1.4,1.5,1.7,1.9,2.7)

1 Общее описание алгоритма

1.1 Свойства и структура алгоритма

В связи с наличием огромного количества накопленной информации задача добычи данных становится все более важной. Кластеризация позволяет распределять данные по группам (кластерам) так, что в каждой группе данные обладают схожими характеристиками, а в разных группах характеристики различаются.

Алгоритм устойчивой кластеризации с использованием связей (robust clustering using links, ROCK [1]) построен на основе понятий связей между кластеризуемыми точками и их соседства. Две точки считаются соседями, если являются достаточно близким (схожими): [math]sim({p_i}, {p_j}) \gt = \theta[/math], где [math]\theta[/math] - заданное пороговое значение в интервале [math](0, 1)[/math]. Связь [math]link({p_i}, {p_j})[/math] между двумя точками определяется как число общих соседей между точками [math]{p_i}[/math] и [math]{p_j}[/math]. Таким образом, чем большее значение функции связи для двух точек, тем более вероятно они принадлежат одному кластеру.

В отличие от алгоритмов кластеризации, учитывающих только локальные характеристики точек, данный алгоритм учитывает глобальную информацию о соседстве при принятии решений о выделении кластеров, что делает его очень устойчивым [1].

ROCK принадлежит к классу иерархических алгоритмов кластеризации. На первом этапе работы алгоритма происходит определение соседей для каждой точки и подсчет количества связей для каждой пары точек. Изначально каждая точка рассматривается в качестве отдельного кластера и для каждого такого кластера рассчитываются значения функции качества,которые используются при последующем слиянии кластеров. Далее в ходе итерационного процесса на каждом шаге выбираются и объединяются два кластера и пересчитываются количество связей и функции качества для нового кластера. По достижении требуемого числа кластеров работа алгоритма завершается.

1.2 Математическое описание алгоритма

Задача кластеризации сводится к выделению такого разбиения точек на кластеры, которое максимизирует сумму связей точек принадлежащих одному кластеру, и минимизирует эту функцию для точек из разных кластеров. Таким образом, для разбияния на [math]k[/math] кластеров необходима максимизация следующей функции.

[math]E_l = \sum_{i=1}^k n_i * \sum_{p_q, p_r \in C_i} \frac{link(p_q, p_r)}{n_i^{1+2f(\theta)}} \qquad(1)[/math]

Данная функция отличается от простой суммы связей для каждого кластера, так как не обеспечивает распределение точек, имеющих мало связей между собой, по разным кластерам. Поэтому действительную сумму связей в кластере следует разделить на ожидаемую сумму связей. Функция [math]f(\theta)[/math] задается пользователем исходя из свойств обрабатываемых данных и ожидаемого характера кластеризации. Она должна обладать следующим свойством: каждая точка, принадлежащая кластеру [math]C_i[/math], имеет приблизительно [math]n_i^{f(\theta)}[/math] соседей в этом кластере.

Связь между двумя кластерами определяется как

[math]link({C_i}, {C_j}) = \sum^{}_{{p_q}\in{C_i}, {p_r}\in{C_j}}{link[{C_i}, {C_j}]}[/math]

Тогда для выбора кластеров для объединения определяется целевая функция качества:

[math]g(C_i, C_j) = \frac{link[C_i, C_j]}{(n_i+n_j)^{1+2f(\theta)} - f_i^{1+2f(\theta)} - f_j^{1+2f(\theta)}}[/math]

Аналогично целевой функции (1) значение связи между двумя кластерами делится на ожидаемое число связей между кластерами.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит из двух частей:

1. Подсчет количества связей между точками;
2. Итеративное объединение кластеров.

Один из возможных подходов к подсчету количества связей основывается на матрице смежности точек: достаточно умножить матрицу смежности на себя, и тогда каждая клетка полученной матрицы будет содержать число связей соответствующей точки.

Итеративная часть алгоритма может быть реализована с помощью структуры данных куча. На каждой итерации с каждым кластером [math]i[/math] связана своя куча [math]q[i][/math], содержащая все связанный с ним кластеры, упорядоченная по убыванию функции качества. Также поддерживается глобальная куча [math]Q[/math], содержащая все кластеры [math]j[/math], упорядоченные по мере убывания функции качества [math]g(j, max(q[j]))[/math], где [math]max(q[j])[/math] - это вершина кучи [math]q[j][/math]. Тогда на каждой итерации объединяются кластер [math]j[/math] с вершины глобальной кучи и кластер [math]q[j][/math]. После объединения необходимо обновить все кучи, содержащие объединенные кластеры, обновить глобальную кучу [math]Q[/math] и создать кучу для нового кластера. Итеративный процесс продолжается до тех пор, пока в глобальной куче [math]Q[/math] не останется требуемое число кластеров.

1.4 Макроструктура алгоритма

Как было описано выше, основную часть каждой итерации алгоритма составляет обновление куч, содержащих сливаемые кластеры.

1.5 Схема реализации последовательного алгоритма

Следующая схема последовательного алгоритма представлена в работе [1] (псевдокод):

 1 procedure cluster(S, k)
 2 begin
 3     link := compute_links(S)
 4     for s in S do
 5     begin
 6         q[s] := build_local_heap(link, s)
 7     end
 8     Q := build_global_heap(S, q)
 9     while size(Q) > k do
10     begin
11         u := extract_max(Q)
12         v := max(q[u])
13         delete(Q, v)
14         w := merge(u, v)
15         for each x in q[u] or q[v] do
16         begin
17             link[x, w] := link[x, u] + link[x, v]
18             delete(q[x], u)
19             delete(q[x], v)
20             insert(q[x], w, g(x, w))
21             insert(q[w], x, g(x, w))
22             update(Q, x, q[x])
23         end
24         insert(Q, w, q[w])
25         deallocate(q[u])
26         deallocate(q[v])
27     end
28 end

1.6 Последовательная сложность алгоритма

Для вычисления количества связей с помощью возведения матрицы в квадрат можно воспользоваться алгоритмом Копперсмита—Винограда [2], вычислительная сложность которого равна [math]O(n^{2,37})[/math] ([math]n[/math] - количество кластеризуемых точек). Для случаев разреженной матрицы смежности в работе [1] описывается алгоритм, имеющий сложность [math]O(n^2 + n{m_m}{m_a})[/math], где [math]{m_a}[/math] и [math]{m_m}[/math] - это среднее и максимальное количество соседей точки соответственно.

Каждая куча может быть построена за время [math]O(n)[/math] [3]. Внешний цикл итерационной части алгоритма исполняется [math]O(n)[/math] раз. Так как на очередной итерации размер каждой локальной кучи в худшем случае может равняться [math]n[/math], то новый кластер должен быть помещен в [math]n[/math] локальных куч, что дает временную сложность вложенного цикла [math]O(n\log{n})[/math]. Таким образом, сложность внешнего цикла в худшем случае будет [math]O(n^2\log{n})[/math].

Итак, оценка времени выполнения алгоритма [math]C_t[/math] задается следующей формулой:

[math]C_t = O(n^{2,37} + n^2\log{n})[/math]

Пространственную сложность подсчета количества связей можно оценить как [math]O(min(n^2, n{m_m}{m_a}))[/math]. Так как при слиянии двух кластеров размер новой кучи не превосходит суммы размеров куч объединяемых кластеров, то пространственная сложность итерационной части алгоритма зависит только от размеров исходных куч и задается формулой:

[math]C_s = O(min(n^2, n{m_m}{m_a}))[/math].

1.7 Информационный граф

Визуализация информационного графа для n = 100 исходных точек и k = 8 требуемых кластеров

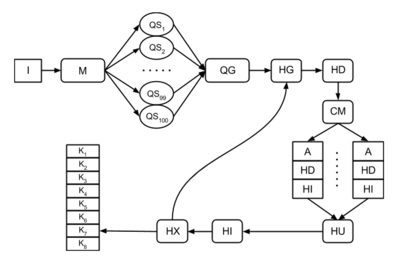
На рисунке представлен информационный граф алгоритма. Используются следующие обозначения:

• I - входные данные
• M - вычисление матрицы связей
• QS - созданиение локальной кучи
• QG - создание глобальной кучи
• HG - взятие элемента/элементов из кучи
• HD - удаление элемента из кучи
• HI - добавление элемента в кучу
• HU - обновление кучи
• HX - удаление куч
• CM - слияние кластеров
• A - арифметические операции
• K - полученный кластер

1.8 Ресурс параллелизма алгоритма

В описанном последовательном алгоритме основной ресурс параллелизма заключается в возможности параллельного вычисления количества связей (например, используя алгоритм параллельного вычисления произведения матриц), создания очередей, и параллельной обработки локальных очередей во внутреннем цикле итерационного этапа алгоритма. В таком случае при распараллеливании алгоритма на [math]p[/math] вычислительных узлов верна следующая оценка времени работы алгоритма:

[math]C_{t_p} = {C_{L_p}} + O(\frac{n^2\log n}{p})[/math],

где [math]{C_{L_p}}[/math] - оценка времени работы выбранного параллельного алгоритма подсчета числа связей.

1.9 Входные и выходные данные алгоритма

Входные данные:

1. Множество [math]n[/math] точек, которые необходимо кластеризовать
2. Пороговое значение [math]\theta[/math] из интервала [math](0, 1)[/math]
3. Требуемое число кластеров [math]k[/math]

Также к входным данным относится информация о характеристиках точек (например в виде таблицы булевых значений принадлежности характеристик точкам).

Выходные данные:

1. [math]n[/math] точек, распределенных по [math]k[/math] кластерам

1.10 Свойства алгоритма

Рассматриваемый алгоритм является детерминированным.

Его вычислительная мощность равна

[math]\frac{O(n^{2,37} + n^2\log n)}{2n+2}[/math]

Отношение последовательной и параллельной сложности:

[math]\frac{O(n^{2,37} + n^2\log n)}{{C_{L_p}} + O(\frac{n^2\log n}{p})}[/math],

где [math]C_{L_p}[/math] - сложность параллельного алгоритма подсчета числа связей (оценки приведены для использования алгоритма Копперсмита—Винограда для вычисления количества связей).

Одним из важных вопросов, влияющих на эффективность алгоритма, является выбор исходных точек. Подход к выбору размера исходного набора точек, достаточного для качественной кластеризации, описывается в работе [4]. Использование случайной стратегии выбора исходных точек помогает алгоритму кластеризации отбрасыванием выпадающих точек (то есть точек, слабо связанных с другими точками). Различные алгоритмы случайного выбора исходных точек рассматриваются в работе [5].

Обработка выпадающих точек в рассматриваемом алгоритме обеспечивается выбором порогового значения [math]\theta[/math]. Также такие точки могут быть принудительно отброшены на последних итерациях алгоритма.

После завершения кластеризации выбранных исходных точек, оставшиеся точки распределяются по кластерам следующим образом. Из каждого кластера выбирается набор точек [math]{L_i}[/math], и очередная точка [math]p[/math] помещается в кластер [math]i[/math], если [math]p[/math] имеет наибольшее число соседей множеством [math]{L_i}[/math].

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

1. Библиотека annoviko/pyclustering включает реализации для Python и C++ под GPL 3
2. Пакет CBA из репозитория CRAN содержит реализацию на R под GPL 2
3. Библиотеки Weka и feed4weka содержат реализацию для Java под GPL 2

3 Литература

[1] Guha S., Rastogi R., Shim K. ROCK: A robust clustering algorithm for categorical attributes //Data Engineering, 1999. Proceedings., 15th International Conference on. – IEEE, 1999. – С. 512-521.

[2] Coppersmith D., Winograd S. Matrix multiplication via arithmetic progressions //Proceedings of the nineteenth annual ACM symposium on Theory of computing. – ACM, 1987. – С. 1-6.

[3] Thomas H. Cormen et al. Introduction to algorithms. – Cambridge : MIT press, 2001. – Т. 6.

[4] Guha S., Rastogi R., Shim K. Cure: an efficient clustering algorithm for large databases //Information Systems. – 2001. – Т. 26. – №. 1. – С. 35-58.

[5] Vitter J. S. Random sampling with a reservoir //ACM Transactions on Mathematical Software (TOMS). – 1985. – Т. 11. – №. 1. – С. 37-57.