Участник:Smirnov.maxim/BIRCH

Авторы: Морозова Светлана, Смирнов Максим. Вклад авторов:

Смирнов максим:

• п.1.5
• п.1.7
• п.1.8
• п.1.9
• п.2.7

Морозова Светлана

• п.1.1
• п.1.2
• п.1.3
• п.1.4
• п.1.6
• п.1.10
• п.3

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Нахождение полезных для анализа закономерностей в больших объёмах данных с недавних пор вызывает значительный интерес. В связи с этим ввелось и стало активно развиваться такое понятие как кластеризация.

Ранние работы и алгоритмы, разработанные в этой области, не уделяли достаточного внимания анализу очень больших наборов данных или минимизации издержек на процессы ввода-вывода. Решением этих проблем стал алгоритм, известный как BIRCH.

BIRCH- алгоритм, применяемый в области Data mining и использующий принципы иерархической кластеризации.

Если имеется очень большой набор данных, то в пространстве он распределен, как правило, неравномерно. Кластерный анализ определяет места наибольшего и наименьшего скоплений, чтобы таким образом понять всю картину целиком. Кроме того, полученные кластеры визуализируются гораздо нагляднее, чем начальные "сырые" данные. Задачей алгоритмов кластеризации является не только простое разбиение данных на кластеры, но и работа в рамках ограниченного объёма доступной памяти (как правило, её объём гораздо меньше, чем размер исходного набора данных) и минимизация времени, требуемого на операции ввода-вывода.

Для наилучшего решения этих проблем BIRCH распределяет входящие данные по кластерам динамически. Для эффективной кластеризации алгоритму требуется всего одно сканирование данных (т.е. с увеличением количества данных сложность увеличивается линейно). А при помощи одной (или более) дополнительных итераций можно и далее улучшать эффективность. BIRCH также является первым алгоритмом, предложенным для эффективного управления "шумами" (данными, которые не вписываются в общее представление модели).

1.2 Математическое описание алгоритма

1.2.1 Теоретическая основа

Пусть в кластере имеются [math]N[/math] точек размерности [math]d[/math]: [math]\{\vec{X_i}\}, i=1,2,...,N[/math]. Тогда центроид [math]{\vec{{X_0}}}[/math], радиус [math]R[/math] и диаметр [math]D[/math] кластера определяются следующим образом:

[math]{\vec{X_0}}=\frac{\sum_{i=1}^N\vec{X_i}}{N}[/math]

[math]R = (\frac{\sum_{i=1}^N{(\vec{X_i} - \vec{X_0})}^2}{N})^{1/2}[/math]

[math]D = (\frac{\sum_{i=1}^N\sum_{j=1}^N{(\vec{X_i} - \vec{X_j})}^2}{N(N-1)})^{1/2}[/math]

[math]R[/math] - это среднее расстояние от каждой точки до центроида. [math]D[/math] - это среднее расстояние между парами в кластере. Данные величины являются альтернативными метриками плотности кластера относительно центроида.

Для измерения близости друг к другу двух кластеров вводятся следующие метрики:

пусть даны центроиды двух кластеров [math]\vec{X_{01}}[/math] и [math]\vec{X_{02}}[/math]. Евклидова метрика [math]D_0[/math] и метрика Манхэттена [math]D1[/math] между двумя кластерами определяются следующим образом:

[math]D_0 = ((\vec{X_{01}}-\vec{X_{02}})^2)^{1/2}[/math]

[math]D_1 = |\vec{X_{01}}-\vec{X_{02}}| = \sum_{i=1}^d |{\vec{X_{01}}}^{(i)}-{\vec{X_{02}}}^{(i)}| [/math]

Пусть имеются два кластера, содержащих соответственно [math]N_1[/math] и [math]N_2[/math] точек размерности [math]d[/math]: [math]\{\vec{X_i}\}[/math], где [math]i= 1,2, ...,N_1[/math] и [math]\{\vec{X_j}\}[/math], где [math]j= N_1+1,N_1+2, ...,N_1+N_2[/math].

Среднее расстояние [math]D_2[/math], среднее внутрикластерное расстояние [math]D_3[/math] и дисперсия [math]D_4[/math] для двух кластеров определяются следующим образом:

[math]D_2 = (\frac{\sum_{i=1}^{N_1}\sum_{j=N_1+1}^{N_1+N_2}{(\vec{X_i} - \vec{X_j})}^2}{N_1N_2})^{1/2}[/math]

[math]D_3 = (\frac{\sum_{i=1}^{N_1+N_2}\sum_{j=1}^{N_1+N_2}{(\vec{X_i} - \vec{X_j})}^2}{(N_1+N_2)(N_1+N_2-1)})^{1/2}[/math]

[math]D_4 = \sum_{k=1}^{N_1+N_2}(\vec{X_k} - \frac{\sum_{i=1}^{N_1+N_2}\vec{X_i}}{N_1+N_2})^2 - \sum_{i=1}^{N_1}(\vec{X_i} - \frac{\sum_{i=1}^{N_1}\vec{X_i}}{N_1})^2 - \sum_{j=N_1+1}^{N_1+N_2}(\vec{X_j} - \frac{\sum_{i=N_1+1}^{N_1+N_2}\vec{X_i}}{N_2})^2[/math]

Таким образом, величины [math]\vec{X_0}[/math], [math]R[/math] и [math]D[/math] относятся к отдельным кластерам, а [math]D_0[/math], [math]D_1[/math], [math]D_2[/math], [math]D_3[/math] и [math]D_4[/math] - к объединению двух кластеров.

1.2.2 Кластерный элемент и кластерное дерево

В основе концепции алгоритма BIRCH лежат понятия кластерного элемента и кластерного дерева (CF Tree).

1.2.2.1 Кластерный элемент

Определение. Пусть в кластере содержатся [math]N[/math] точек размерности [math]d[/math]:[math]\{\vec{X_i}\}[/math], где [math]i=1,2,...,N[/math]. Кластерный элемент (CF) - тройка чисел, характеризующая информацию о кластере: [math]CF = (N, \vec{LS}, SS)[/math], где [math]N[/math] - количество элементов входных данных, содержащихся в кластере, [math]\vec{LS}[/math] - линейная сумма входных данных (т.е. [math]\sum_{i=1}^{N}\vec{X_i}[/math]), [math]SS[/math] - сумма квадратов входных данных (т.е. [math]\sum_{i=1}^{N}{\vec{X_i}}^2[/math])

Теорема Пусть [math]CF_1 = (N_1, \vec{LS_1}, SS_1)[/math] и [math]CF_2 = (N_1, \vec{LS_2}, SS_2)[/math] - CF векторы двух непересекающихся кластеров. Тогда при их объединении образуется кластер со следующим CF вектором:

[math]CF = CF_1 + CF_2 = (N_1+N_2, \vec{LS_1}+\vec{LS_2}, SS_1+SS_2)[/math].

Из указанных выше определения и теоремы вытекает тот факт, что при объединении кластеров их CF вектор может вычисляться инкрементно и точно. Легко показать, что вычислить величины [math]\vec{X_0}[/math], [math]R[/math], [math]D[/math], [math]D_0[/math], [math]D_1[/math], [math]D_2[/math], [math]D_3[/math], [math]D_4[/math], как и обычные метрики, также не составит труда.

Таким образом, в данном случае информацией о кластере является не весь набор точек, а вектор CF. Хранение одного только вектора может показаться неэффективным, но этого вполне достаточно для оперирования всеми необходимыми метриками, на основе которых принимаются решения в алгоритме BIRCH.

1.2.2.2 Кластерное дерево

Определение. Кластерное дерево (CF Tree) - это взвешенно сбалансированное дерево с двумя параметрами: [math]B[/math] - коэффициент разветвления, [math]T[/math] - пороговая величина.

Каждый нелистьевой узел дерева имеет не более чем [math]B[/math] вхождений узлов следующей формы: [math][CF_i,child_i][/math], где [math]i=1,2,...,B[/math], child - указатель на i-й дочерний узел, [math]CF_i[/math] - CF вектор соответствующего подкластера.

Каждый листьевой узел имеет ссылку на два соседних узла (prev и next) для того, чтобы связать все узлы для эффективного сканирования. Все листьевые узлы должны удовлетворять пороговому ограничению [math]T[/math], т.е. диаметр (радиус) не должен превосходить [math]T[/math]. В процессе вставки новых данных CF дерево строится динамически. Оно использует вставку данных для кластеризации точно также как [math]B+[/math] дерево использует её для поиска. CF дерево очень компактно, поскольку каждый листьевой узел - это не просто точка, а подкластер (который объединяет множество точек с учётом ограничения [math]T[/math]).

1.2.2.3 Операция вставки в CF дерево

Опишем алгоритм вставки элемнта [math]Ent[/math] в CF дерево:

1) Определение подходящего листа: Начиная с корня, алгоритм рекурсивно спускается по CF дереву, выбирая ближайший дочерний узел в соответствии с выбранной метрикой [math]D0[/math], [math]D1[/math], [math]D2[/math], [math]D3[/math] или [math]D4[/math].

2) Преобразование листа: Когда алгоритм доходит до листа, он находит ближайшую листьевой элемент, скажем, [math]L_1[/math], а затем проверяет, можно ли добавить Ent к [math]L_1[/math] без нарушения порогового условия. Если да, то с учётом этого изменяется CF вектор для [math]L_1[/math]; если нет, то Ent становится новым элементом листа. Если в листе для этого достаточно места, то шаг окончен, иначе он должен "расщепиться". Расщепление узла производится при помощи выбора за основу наиболее удалённой друг от друга пары элементов и перераспределение оставшихся элементов в соответствии с выбранным критерием близости.

3) Преобразование пути к листу: После вставки Ent в лист мы должны обновить информацию о CF для каждого нелистьевого элемента на пути к листу. При отсутствии расщепления это означает простое сложение CF векторов для отражения факта добавления Ent. Расщепление листа же требует вставки нового нелистьевого элемента в родительский узел для задания только что созданного листа. Если у родителя есть место для этого элемента, то необходимо просто преобразовать CF векторы на всех более высоких уровнях. В общем случае, однако, нам также придётся расщепить родительский узел, и так далее до корня. Если расщеплён корень, то высота дерева увеличивается на единицу.

4) Улучшение слияния: Расщепление вызвано ограничением на размер узла, который не зависит от кластеризационных свойств данных. Если во входящем потоке присутствуют "искажённые" (из областей с низкой плотностью) данные, это может повлиять на качество кластеризации, а также уменьшить эффективность использования памяти. Дополнительный шаг алгоритма помогает решить эти проблемы: предположим, что произошло расщепление листа, и распространение этого процесса остановилось на некотором нелистьевом узле [math]N_j[/math], то есть [math]N_j[/math] может вместить дополнительный элемент, полученный после расщепления. Теперь мы сканируем узел [math]N_j[/math] для нахождения двух наиболее близких элементов. Если это не пара, отвечающая расщеплению, мы пытаемся объединить их и поставить в соответствие два дочерних узла. Если количество элементов в дочерних узлах больше B, мы снова расщепляем результат объединения. В процессе повторного расщепления, в случае, если один источник собирает достаточно элементов для того, чтобы полностью заполнить узел, оставшиеся элементы передаются другом источнику. В итоге, если объединённые элементы помещаются в одном узле, в нём освобождается место для ещё одного элемента. Тем самым увеличивается степень использования свободного пространства и откладывается дальнейшее расщепление. В ином случае мы улучшаем распределение элементов в двух ближайших подкластерах.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма заключается в многократном выполнении операции вставки нового элемента в дерево, в процессе чего требуется вычисление следующих величин:

• радиуса [math]R[/math] или диаметра [math]D[/math] кластерного элемента. Выполняется при попытке вставить новый элемент в один из подкластеров листьевого узла дерева.

• расстояния между двумя элементами. Выполняется при поиске ближайшего по отношению к новому элементу подкластера в узле дерева по одной из рассмотренных в разд. 1.2.1 метрик [math]D_0[/math], [math]D_1[/math], [math]D_2[/math], [math]D_3[/math] или [math]D_4[/math].

Зная характеристики кластерных элементов [math]N[/math], [math]\vec{LS}[/math] и [math]S[/math], в результате алгебраических преобразований можно получить следующие упрощенные формулы вычисления необходимых значений:

[math]\vec{X_0} = \frac{\vec{LS}}{N}[/math]

[math]R = (\frac{SS - 2\vec{X_0}\vec{LS} + N(\vec{X_0})^2}{N})^{1/2}[/math]

[math]D = (\frac{2(N*SS - (\vec{LS})^2)}{N(N-1)})^{1/2}[/math]

[math]D_2 = (\frac{N_1*SS_2 + N_2*SS_1 - 2\vec{LS_1}\vec{LS_2}}{N_1*N_2})^{1/2}[/math]

[math]D_3 = (\frac{2((N_1+N_2)(SS_1+SS_2)-(\vec{LS_1}+\vec{LS_2})^2)}{(N_1+N_2)(N_1+N_2-1)})^{1/2}[/math]

1.4 Макроструктура алгоритма

Реализация алгоритма BIRCH состояит из следующих четырёх фаз:

• Фаза 1. Главной задачей фазы 1 является сканирование всех данных и построение в памяти исходного CF дерева, используя заданное количество памяти. Это дерево стремится отразить информацию о кластеризации данных настолько хорошо, насколько это позволяют ограничения по памяти. При этом плотно распределённые данные группируются в подкластеры, а более разрозненные данные удаляются. После завершения фазы 1 вспомогательные вычисления в дальнейших фазах будут:

1) быстрее, потому что (а) больше не нужны операции ввода-вывода, (b) проблема кластеризации начальных данных упрощается до проблемы кластеризации подкластеров в листьях;

2) точнее, потому что (а) большинство данных с низкой плотностью удалены, (b) оставшиеся данные распределены оптимально (в соответствии с доступным количеством памяти);

• Фаза 2. Данная фаза является опциональной. Известно, что существующие методы глобальной кластеризации, используемые в рамках фазы 3, имеют различные диапазоны входных значений, при которых их реализация наиболее эффективна. Поэтому потенциально существует пробел между размером фазы 1 и входными значениями фазы 3. И фаза 2 как раз является недостающим связующим звеном: так же как и фаза 1, она сканирует листьевые элементы начального CF дерева для того, чтобы построить меньшее дерево, удаляя ещё больше элементов с низкой плотностью и группируя переполненные подкластеры в большие кластеры.

• Фаза 3. В данной фазе для листьевых элементов применяется (любой подходящий) алгоритм глобальной кластеризации. Существующие алгоритмы кластеризации наборов точек могут также работать с наборами подкластеров, каждый из которых представлен своим CF вектором. Зная CF вектор, можно вычислить центроид и в дальнейшем заменить всю информацию о кластере этим значением (этого достаточно для вычисления большинства необходимых метрик). После фазы 3 мы получаем набор кластеров, который отражает основные характеристики распределяемых данных.

Однако, всё ещё могут оставаться некоторые неточности, для устранения которых существует фаза 4.

• Фаза 4. Данная фаза является опциональной и влечёт за собой затраты на дополнительное сканирование данных для корректировки неточностей и дальнейшего улучшения кластеризации. Фаза 4 использует центроиды кластеров, полученные в фазе 3 для как основы и перераспределяет точки входных данных в ближайшие для них основы для получения нового списка кластеров. Фаза 4, если это необходимо пользователю, может быть расширена дополнительными проходами для уверенности в том, что результат приближается к оптимальному.

1.5 Схема реализации последовательного алгоритма

Последовательную реализацию основных операций алгоритма BIRCH можно продемонстрировать на примере следующего фрагмента кода на языке C++:

void CF_Node::insert(const CF_Cluster &entry)
{
    //Находим ближайший к новому элементу подкластер в узле
    СF_Vector_it closest = entry.findClosest(subclusters);
    //Если узел пустой, добавляем в него новый подкластер
    if (closest == subclusters.end()) {
        subclusters.push_back(entry);
        return;
    }
    closest->add(entry);
    //Если узел является листьевым, и ближайший подкластер не может вместить
    //новый элемент, добавляем в узел новый подкластер
    if (leaf) {
        if (closest->D > threshold) {
            closest->remove(entry);
            subclusters.push_back(entry);
        }
    }
    else {
        CF_Node *node = closest->child;
        node->insert(entry);
        //Если при добавлении нового элемента в дочерний узел тот переполнился,
        //расщепляем его        
        if (node->getSubclusters().size() > bFactor) {
            CF_Vector newClusters = node->splitNode();
            delete node;
            subclusters.erase(closest);
            subclusters.insert(subclusters.end(), newClusters.begin(), newClusters.end());
        }
    }
    //Если узел является корневым и он переполнен, расщепляем его
    if (root && subclusters.size() > bFactor) {
        subclusters = splitNode();
        leaf = false;
    }
}

CF_Vector CF_Node::splitNode()
{
    if (subclusters.size() < 2)
        return (root) ? subclusters : CF_Vector{CF_Cluster(this)};
    //Находим пару наиболее удаленных друг от друга подкластеров
    CF_Vector_it pole1, pole2;
    data_t longestDist = 0.0;
    for (auto lhs = subclusters.begin(); lhs != subclusters.end() - 1; ++lhs) {
        for (auto rhs = lhs + 1; rhs != subclusters.end(); ++rhs) {
            auto distance = getDistance(*lhs, *rhs);
            if (distance > longestDist) {
                longestDist = distance;
                pole1 = lhs;
                pole2 = rhs;
            }
        }
    }
    //Разделяем множество всех подкластеров узла на две части
    CF_Vector subclusters1, subclusters2;
    for (auto it = subclusters.begin(); it != subclusters.end(); ++it) {
        if (getDistance(*it, *pole1) < getDistance(*it, *pole2))
            subclusters1.push_back(*it);
        else
            subclusters2.push_back(*it);
    }
    //Создаем два новых узла
    CF_Node *node1 = new CF_Node(threshold, bFactor, count, leaf, subclusters1),
            *node2 = new CF_Node(threshold, bFactor, count, leaf, subclusters2);
    //Связываем листья
    if (leaf) {
        if (prevLeaf) {
            node1->setPrevLeaf(prevLeaf);
            prevLeaf->setNextLeaf(node1);
        }
        if (nextLeaf) {
            node2->setNextLeaf(nextLeaf);
            nextLeaf->setPrevLeaf(node2);
        }
        node1->setNextLeaf(node2);
        node2->setPrevLeaf(node1);
    }
    CF_Cluster cluster1(node1), cluster2(node2);
    return CF_Vector{cluster1, cluster2};
}

1.6 Последовательная сложность алгоритма

Для начала проанализируем вычислительную сложность фазы 1. Максимальный размер дерева [math]\frac{M}{P}[/math], где [math]P[/math] - ограничение по памяти на размер узла, а [math]M[/math] - общий объем памяти. Для того чтобы вставить элемент, мы должны пройти путь от корня до листа (это около [math]1+log_B\frac{M}{P}[/math] узлов). В каждом узле в поисках "ближайшего" нам необходимо просмотреть B элементов; сложность для каждого элемента пропорциональна размерности d.

Поэтому сложность вставки всех входных точек [math]O(d \cdot N \cdot B(1+log_B\frac{M}{P}))[/math].

В случае, когда необходимо перестроить дерево, предположим, что ES - это размер CF элемента. Существует максимум [math]\frac{M}{ES}[/math] листьевых элементов для вставки, поэтому сложность повторной вставки листьевых элементов [math]O(d \cdot \frac{M}{ES} \cdot B(1+log_B\frac{M}{P}))[/math].

Количество итераций перестройки дерева зависит от пороговой величины. На самом деле, это около [math]log_2\frac{N}{N_0}[/math] (двоичное основание появилось из-за того, что мы не можем провести оценку более чем в 2 раза отличающуюся от текущего размера). [math]N_0[/math] - это число входных точек, загруженных в память с пороговым ограничением [math]T_0[/math].

Соответственно, итоговая сложность фазы 1 [math]O(d \cdot N \cdot B(1+log_B\frac{M}{P})+log_2\frac{N}{N_0} \cdot d \cdot \frac{M}{ES} \cdot B(1+log_B\frac{M}{P}))[/math].

Анализ фазы 2 проводится аналогично.

Что касается операций ввода-вывода, то в фазе 1 данные сканируются один раз, а в фазе 2 не сканируются вовсе. Некоторое количество вычислений связано с удалением точек из областей с низкой плотностью. Если количество доступной для этой операции памяти не больше M и проведено порядка [math]log_2\frac{N}{N_0}[/math] перестроек дерева, то сложность ввода-вывода для фазы 1 существенно не отличается от сложности чтения из файла. Основываясь рассуждениях выше, сложность фаз 1 и 2 будет линейно увеличиваться с ростом N.

В фазе 3 нет операций ввода-вывода. Её сложность ограничена константой, которая зависит от максимального размера входных данных, и варианта выбранного алгоритма для кластеризации.

Фаза 4 снова сканирует данные и записывает каждую точку в подходящий кластер; время работы пропорционально [math]N \cdot K[/math].

[math][/math]

1.7 Информационный граф

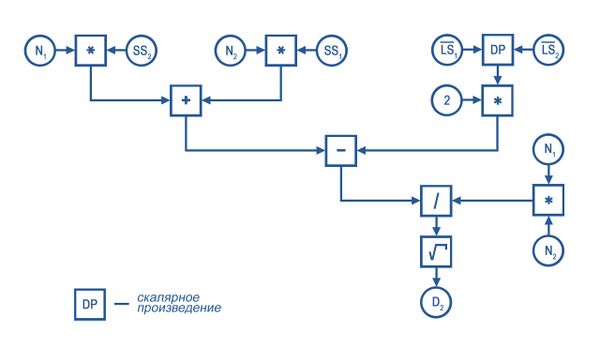
1.7.1 Вычисление расстояния

[math]D_2=\frac{N_1\cdot SS_2+N_2\cdot SS_1-2 \cdot \vec{LS_1}\cdot \vec{LS_2}}{N_1\cdot N_2}[/math], где

[math]CF_1=[N_1,\vec{LS_1},SS_1][/math]

[math]CF_2=[N_2,\vec{LS_2},SS_2][/math]

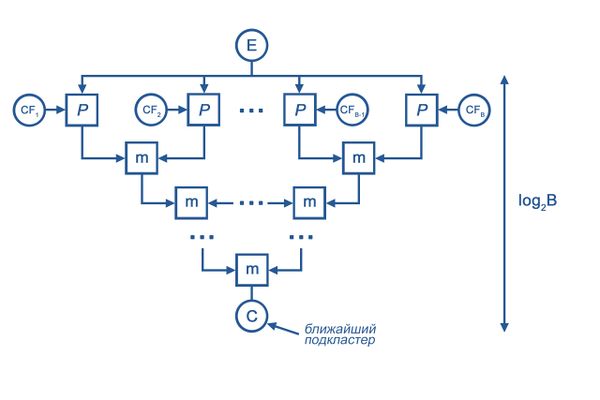
1.7.2 Поиск ближайшего подкластера

[math]E[/math] - новый элемент

[math]CF_i, i = 1,...,B[/math] - подкластеры узла

[math]m[/math] - операция min

[math]\rho[/math] - нахождение расстояния

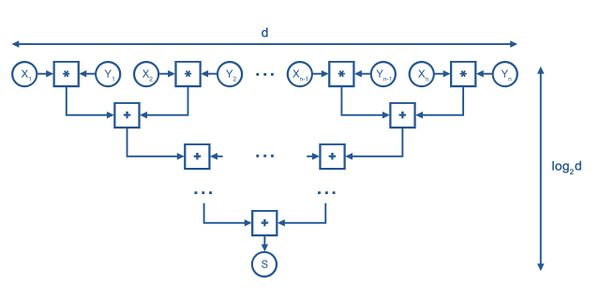
1.7.3 Скалярное произведение

[math]s = \vec{x}\cdot\vec{y}=\sum_{i=1}^d x_i\cdot y_i[/math]

[math][/math]

1.8 Ресурс параллелизма алгоритма

Параллельно могут быть выполнены следующие шаги алгоритма:

• Нахождение ближайшего к новому элементу подкластера в узле при выполнении операции вставки. Это возможно за счет того, что расстояние между парами элементов может быть вычислено независимо друг от друга.
• Вычисление величин [math]\vec{LS},\vec{X0}, R, D, D_0-D_4[/math], в процессе чего выполняются операции сложения и скалярного произведения векторов.

Таким образом, параллельная сложность фазы 1 алгоритма будет равна [math]O((N + log_2\frac{N}{N_0} \cdot \frac{M}{ES})(log_2 B + log_2 d)(1+log_B\frac{M}{P}))[/math]

Другим способом параллелизации алгоритма может служить создание и заполнение сразу множества кластерных деревьев, между которыми будут распределены входные данные. Множество всех подкластеров листьевых узлов полученных таким образом деревьев может быть подвергнуто глобальной кластеризации с помощью какого-либо из известных параллельных алгоритмов, например, k-средних.

1.9 Входные и выходные данные алгоритма

Входные данные: набор из [math]N[/math] точек [math]\{X_i\}, i=1,...,N[/math] размерности [math]d[/math].

Объем входных данных: [math]N \cdot d[/math]

Выходные данные: кластерное дерево с не более чем [math]\frac{M}{P}[/math] узлами.

Объем выходных данных: [math]M[/math]

1.10 Свойства алгоритма

1.10.1 Вычислительная сложность

Вычислительная сложность алгоритма имеет порядок [math]O(\frac{d \cdot B \cdot (1+log_B\frac{M}{P}) \cdot (N +log_2\frac{N}{N_0} \cdot \frac{M}{ES})}{N \cdot d + M})[/math]

1.10.2 Достоинства алгоритма

По сравнению с предыдущими методами BIRCH обладает следующими достоинствами:

1. BIRCH является локальным алгоритмом, то есть каждое решение о каждом элементе кластера принимается без повторного сканирования данных или уже существующих кластеров. Используются только метрики, отражающие близость элементов друг к другу.

2. BIRCH использует факт неравномерного распределения данных в пространстве и поэтому не все данные рассматриваются как одинаково важные для построения кластера. Области с большой плотностью обрабатываются как единый кластер. Данные в более разреженных областях могут удаляться (опционально).

3. BIRCH использует всю доступную память для получения наилучших из возможных подкластеров, в то же время минимизируя затраты на операции ввода/вывода. Оптимизация процесса кластеризации достигается за счет использования взвешенно-сбалансированного дерева. При этом время исполнения линейно.

4. BIRCH не требует всего набора данных заранее (при этом просматривает его всего один раз).

1.10.3 Недостатки алгоритма

1. Алгоритм позволяет работать только с числовыми данными.

2. BIRCH хорошо выделяет только кластеры сферической формы.

3. Существует необходимость в задании пороговых значений.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

В составе пакетов и библиотек:

• scikit-learn
• NU-MineBench

Пользовательские реализации:

• JBIRCH