Участник:Elena777mc/Плотностный алгоритм кластеризации DBSCAN: различия между версиями
Sleo (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
| − | {{Assignment}} | + | {{Assignment|Sleo}} |
| − | |||
{{algorithm | {{algorithm | ||
| name = Плотностный алгоритм кластеризации DBSCAN | | name = Плотностный алгоритм кластеризации DBSCAN | ||
Версия 01:53, 14 ноября 2016
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 14.11.2016 Данная работа соответствует формальным критериям. Проверено Sleo. |
| Плотностный алгоритм кластеризации DBSCAN | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n \log n)[/math] |
| Объём входных данных | [math]n[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(|X| \log |X|)[/math] |
| Ширина ярусно-параллельной формы | [math]O(m)[/math] |
Основные авторы описания: Малахова Е.С. (1.2,1.4-1.8,2.7), Сагиолданова Ж. (1.1-1.3,1.9-1.10,3)
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Кластеризация – это процесс разбиения множества с [math]N[/math] элементами [math]x_1, x_2, ... , x_n (x_n[/math] имеет размерность [math]m[/math]) на [math]K[/math] кластеров, так, чтобы в каждом кластере все элементы были схожи в каком-то смысле. [math]x_i[/math] могут быть числовыми, категориальными или смешанными данными. В плотностных методах кластеры рассматриваются как регионы пространства данных с высокой плотностью объектов, которые разделены регионами с низкой плотностью объектов.
Алгоритм DBSCAN (Density Based Spatial Clustering of Applications with Noise) [1] –плотностной алгоритм для кластеризации пространственных данных с присутствием шума, был предложен Мартином Эстер, Гансом-Питером Кригель и их коллегами в 1996 году как решение проблемы разбиения (изначально пространственных) данных на кластеры произвольной формы.
Большинство алгоритмов, производящих плоское разбиение, создают кластеры по форме близкие к сферическим, так как минимизируют расстояние точки до центра кластера.
Авторы DBSCAN экспериментально показали, что их алгоритм способен распознать кластеры различной формы. Идея, положенная в основу алгоритма, заключается в том, что внутри каждого кластера плотность точек (объектов) заметно выше, чем плотность снаружи кластера, а также плотность в областях с шумом ниже плотности любого из кластеров. Еще точнее, для каждой точки кластера ее окрестность в диапазоне заданного радиуса должна содержать не менее некоторого числа точек, которое задается пороговым значением.
1.2 Математическое описание алгоритма
Исходные данные: объекты, которые нужно кластеризовать, параметры [math]MinPts, \ \varepsilon[/math] . Между объектами можно считать расстояния.
Вычисляемые данные: разбиение объектов по кластерам. Количество кластеров зависит от исходных данных. [3]
Для построения оценки плотности, на основе соседства точек вводятся понятия достижимости и связности. Под [math]\varepsilon [/math] -соседями точки [math]x \in X[/math] понимается множество точек, расстояние до которых не превышает [math]\varepsilon [/math], т. е.
[math]N_\varepsilon (x) = \{y \in X | D(x, y) \le \varepsilon\}[/math].
Тогда точка [math]y[/math] достижима из точки [math]x[/math], если существует последовательность точек [math]x^{(1)}=x, x^{(2)},... , x^{(p-1)}, x^{(p)}=y[/math], для которой выполнено:
- [math] \begin{align} x^{(i+1)} \in N_\varepsilon (x^{(i)}), i=1,... ,p-1 \\ \mid N_\varepsilon (x^{(i)}) \mid \ge MinPts, i=1,... ,p-1 \end{align} [/math]
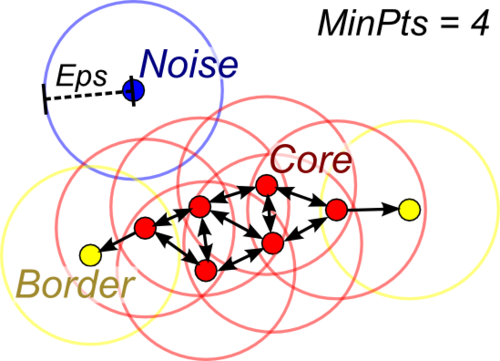
Здесь значение [math]MinPts[/math] задаётся пользователем и регулирует порог «шума». Согласно второму условию, у точек, находящихся внутри кластера, должно быть не менее [math]MinPts \ \varepsilon[/math] -соседей. Такие точки называются «ядрами». Остальные точки разделяются на граничные (имеющие менее [math]MinPts \ \varepsilon [/math] -cоседей, но достижимые из какого-либо «ядра») и шумовые. Две точки связны, если существует «ядро», из которого они обе достижимы. При такой постановке задачи, под кластером понимается максимальное связное подмножество множества [math]X[/math] . Точки, не попавшие в какой-либо кластер (не принадлежащие [math]\varepsilon[/math] -окрестности какого-либо «ядра»), относятся к классу «шум».
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является нахождение [math]\varepsilon[/math]-соседей каждого объекта входного множества [math]X[/math]. На эту часть алгоритма приходится основное время работы алгоритма, так как требуется найти всех соседей для каждого объекта заданного множества. Основные операции, которые применяются в вычислительном ядре алгоритма: нахождение расстояние между объектами и сравнение расстояния с порогом для определения того, являются ли данные объекты [math]\varepsilon[/math]-соседями.
1.4 Макроструктура алгоритма
Алгоритм DBSCAN использует пространственную структуру данных для определения соседних объектов. Это может быть R*-дерево или kd-дерево. Такие структуры данных позволяют найти все объекты в пределах определенного расстояния от текущего объекта. Сложность построения таких структур [math]O(n \log n)[/math], и использование такой структуры не увеличит сложность всего алгоритма (если сложность самого алгоритма [math]O(n \log n)[/math]). Также для построения таких деревьев нужно уметь находить расстояния между объектами [math]\rho(u,v)[/math], это расстояние можно вводить разными способами. Например, если [math]\rho(u,v)[/math] - метрика в евклидовом пространстве, [math]u=(u_1,...,u_n)[/math] и [math](v_1,...,v_n)[/math], то расстояние вычисляется следующим образом: [math]\rho(u,v)=\sqrt{(u_1-v_1)^2+(u_2-v_2)^2+...+(u_n-v_n)^2} = \sqrt{\sum_{k=1}^n(u_k-v_k)^2}[/math]
1.5 Схема реализации последовательного алгоритма
Последовательная реализация алгоритма может быть представлена следующим псевдокодом:
// Основная функция, которая реализует алгоритм кластеризации [math]DBSCAN(X, \varepsilon, MinPts)[/math] //Изначально все объекты в [math]X[/math]не кластеризованы [math]FORALL[/math] objects [math]x[/math] in [math]X\ DO[/math] [math]IF\ x[/math] is unclassified call function [math]expand\_cluster[/math] to construct a cluster wrt. [math]\varepsilon[/math] and [math]MinPts[/math] containing [math]x[/math]
// Вспомогательная функция, которая строит кластер на основе одной точки [math]FUNCTION\ expand\_cluster(x,X,\varepsilon, MinPts):[/math] [math]retrive\_\varepsilon neighborhood(x, \varepsilon)[/math]; [math]IF \mid N_{\varepsilon}(x) \mid \lt MinPts[/math] //т.е. [math]x[/math] - не ядровой объект mark [math]x[/math] as [math]noise[/math] and [math]RETURN[/math]; [math]ELSE[/math]//т.е. [math]x[/math] - ядровой объект select a new cluster-id and mark all objects in [math]N_{\varepsilon}(x)[/math] with this current [math]cluster-id[/math]; push all objects from [math]N_{\varepsilon}(x)[/math]\[math](x)[/math] onto the stack seeds; [math]WHILE\ NOT[/math] seeds.empty() [math]DO[/math] [math]currentObject[/math] := seeds.top(); seeds.pop(); [math]retrive\_\varepsilon neighborhood(currentObject, \varepsilon)[/math]; [math]IF \mid N_{\varepsilon}(currentObjects) \mid \ge MinPts[/math] select all objects in [math]N_{\varepsilon}(currentObject)[/math] not yet classified or marked as [math]noise[/math], push the unclassified objects onto seeds and mark all of these objects with current [math]cluster-id[/math]; [math]RETURN[/math]
// Вспомогательная функция, для определения [math]\varepsilon[/math]-соседей для объекта [math]FUNCTION\ retrive\_\varepsilon neighborhood(x, \varepsilon)[/math] //функция возвращает соседей на основе пространственной структуры данных return [math]\{ x' \ | \ \forall x' \in X: \rho(x, x') \lt \varepsilon \}[/math]
1.6 Последовательная сложность алгоритма
Для того, чтобы алгоритм мог кластеризовать все объекты, необходимо пройти по каждому из них хотя бы один раз. Если использовать R*-дерево или kd-дерево для определения соседних объектов со сложностью [math]O(\log n)[/math], то сложность алгоритма [math]O(n \log n)[/math]. Если не использовать эти структуры, то в худшем случае алгоритм будет иметь сложность [math]O(n^2)[/math], так как придется считать полную матрицу расстояний между объектами.
1.7 Информационный граф
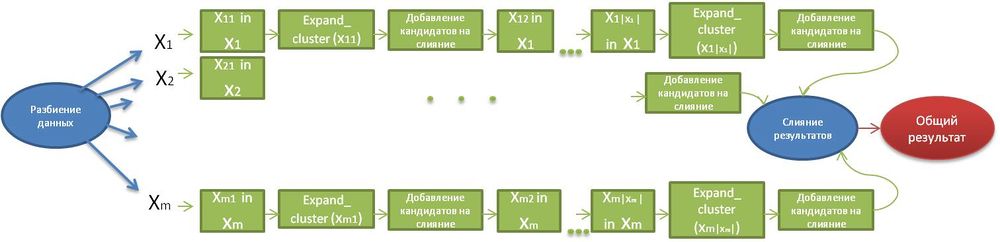
В настоящем алгоритме осуществляется параллелизм по данным. Ниже представлена общая структура данного алгоритма.
Разбиение данных происходит с помощью пространственной структуры данных (R*-дерево, kd-дерево), которая разбивает все множество объектов [math]X[/math] на [math]m[/math] частей: [math]X_1,X_2,...,X_m[/math].
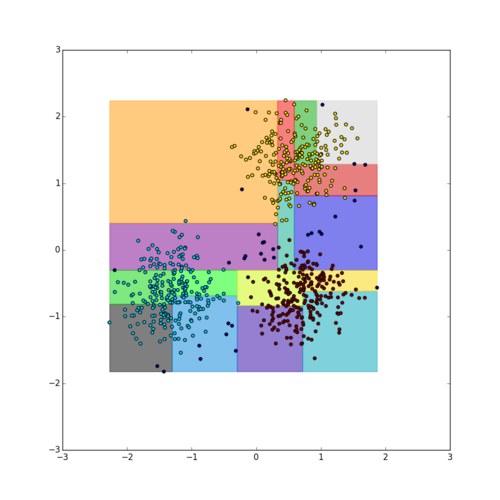
На каждой части объектов применяется алгоритм PDBSCAN (каждая часть использует пространственную структуру данных, которая распределяется вместе с каждой частью данных). Данный алгоритм отличается от общего алгоритма DBSCAN тем, что применяется к части объектов и для каждой из этих частей определяет кандидатов на слияние. Если для ядрового объекта части [math]X_i[/math] в [math]\varepsilon[/math]-окрестности находится объект из другой части [math]X_j[/math], то такие объекты становятся кандидатами на слияние.
Само слияние осуществляется следующим образом: для каждой пары кандидатов на слияние, объединяем кластеры, соответствующие этим кандидатам в один общий кластер.
1.8 Ресурс параллелизма алгоритма
Как видно из общей структуры графа алгоритма, ширина ярусно-параллельной формы алгоритма [math]O(m)[/math], где m - количество частей, на которые разбиваются все входное множество объектов [math]X[/math]. Высотой ярусно-параллельной формы алгоритма является [math]O(|X| \log |X|)[/math], где [math]\mid X \mid[/math] - максимальное количество среди числа объектов в каждой части разбиения. Именно такую сложность имеет алгоритм PDBSCAN, применяемый к каждой отдельной части разбиения.
1.9 Входные и выходные данные алгоритма
Входные данные: множество точек X из n-мерного пространства, на котором определена функция расстояния D. В наиболее распространенном случае пространственной кластеризации используется Евлидова метрика между векторами из [math]{R}^n[/math].
Объём входных данных: n (размерность входящего множества)
Выходные данные: размеченное множество точек X, в котором каждой точке соответствует номер ее кластера. Обычно каждой точке из X сопоставляется ее номер, а на выходе алгоритм дает отображение номеров точек в номера соответствующих им кластеров, например в виде вектора размера |X|
Объём выходных данных: n (размерность выходящего множества)
1.10 Свойства алгоритма
Вычислительная мощность, как отношение числа операций к суммарному объему входных и выходных данных логарифмическая.
Преимущества алгоритма
- алгоритм может обрабатывать большой объем данных и не зависит от порядка ввода данных;
- может определять кластера произвольной формы;
- параллельная реализация сбалансирована по количеству и виду производимых операций (вычисление расстояния, сравнение с [math]\varepsilon[/math]);
- не требуется задание числа кластеров;
- может выделять кластеры в присутствии «шума»и выбросов [5];
- число итераций определяется заранее.
Недостатки алгоритма
- не может выделять кластеры сложной структуры, например, имеющие разную плотность, так как параметры алгоритма не могут быть выбраны отдельно для каждого кластера;
- не может построить иерархическую структуру кластеров;
- не детерминирован, так как граничные точки, достижимые из более, чем одного кластера, могут быть частью любого из них в зависимости от порядка обрабатываемых данных. Однако такая ситуация возникает редко, а относительно ядровых точек и шума DBSCAN детерминирован.
- плохо работает на кластерах, которые имеют небольшое пересечение между собой.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- Scikit learn (Python, последовательная реализация)
- Northwestern University (C++, параллельная реализация kd-tree)
- github/ContinuumIO (Python, параллельная реализация)
- github/propanoid (C++, последовательная реализация VP tree)
- github/dparks1134 (С++, последовательная реализация)
- Disjoint-Set Data Structure based Parallel DBSCAN (C++ параллельная реализация kd-tree)
- github/bwoneill (Spark/Python параллельная реализация kd-tree)
- github/alitouka (Spark/Scala параллельная реализация)
- CRAN (R, последовательная реализация)
3 Литература
<references \> <references \>(A Fast Parallel Clustering Algorithm for Large Spatial Databases, JOCHEN JAGER, HANS-PETER KRIEGEL)
<references \>(АЛГОРИТМЫ КЛАСТЕРИЗАЦИИ В ЗАДАЧАХ СЕГМЕНТАЦИИ СПУТНИКОВЫХ ИЗОБРАЖЕНИЙ, Пестунов Игорь Алексеевич, Синявский Юрий Николаевич)
- ↑ A density-based algorithm for discovering clusters in large spatial database / M. Ester, H.-P. Kriegel, J. Sander, X. Xu // Proc. 1996 Intern. Conf. on Knowledge Discovery and Data Mining. – 1996. – P. 226 – 231.
- ↑ http://stats.stackexchange.com/questions/194734/dbscan-what-is-a-core-point
- ↑ "Xu, X. A fast parallel clustering algorithm for large spatial databases / X. Xu, M. Ester, H.-P. Kriegel // Proc. 1999 Intern. Conf. on Knowledge Discovery and Data Mining. – 1999. – Vol. 3, is. 3. – P. 263 – 290.
- ↑ https://github.com/bwoneill/pypardis/blob/master/plots/median_search_split/clusters_partitions.png
- ↑ АЛГОРИТМЫ КЛАСТЕРИЗАЦИИ В ЗАДАЧАХ СЕГМЕНТАЦИИ СПУТНИКОВЫХ ИЗОБРАЖЕНИЙ/ И. А. Пестунов, Ю. Н. Синявский// Вестник Кемеровского государственного университета. – 2012. – P. 263– 299.