Участник:Elmon/Плотностный алгоритм кластеризации DBSCAN: различия между версиями
Elmon (обсуждение | вклад) (Баг с блоком {{Assignment}} в конце статьи, переместил в начало) |
Sleo (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | + | {{Assignment|Sleo}} | |
| − | {{Assignment}} | ||
{{algorithm | {{algorithm | ||
Версия 02:25, 14 ноября 2016
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 14.11.2016 Данная работа соответствует формальным критериям. Проверено Sleo. |
| Плотностный алгоритм кластеризации DBSCAN | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n \log n)[/math] |
| Объём входных данных | [math]n[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(|H| \log |H|)[/math] |
| Ширина ярусно-параллельной формы | [math]O(w)[/math] |
Основной автор описания: Гилевич В.В.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Кластеризация — это процедура, упорядочивающая элементы из некоторого множества в сравнительно однородные группы (кластеры). Элементы могут содержать числовые, категориальные или смешанные данные. Плотностные методы выделяют кластеры на основе следующей идеи: кластером считается регион с высокой плотностью объектов, которые разделены разреженными регионами (с низкой плотностью объектов)
Алгоритм DBSCAN (Density Based Spatial Clustering of Applications with Noise) [1] — плотностной алгоритм для кластеризации пространственных данных с присутствием шума, был предложен Мартином Эстер, Гансом-Питером Кригель и их коллегами в 1996 году как решение проблемы разбиения данных на кластеры произвольной формы.
Алгоритм имеет ряд отличительных свойств:
- Не требуется заранее определять число кластеров
- Может отличать кластеры, которые нельзя разделить прямой линией (плоскостью, для N-мерного пространства), в том числе кластера, частично или полностью окруженные другим кластером.
- Хорошо работает в условиях зашумленных входных данных
1.2 Математическое описание алгоритма
1.2.1 Исходные данные
Множество [math]X[/math], на котором определена функция расстояния [math]D[/math].
1.2.2 Вычисляемые данные
Множество пар из элемента множества [math]X[/math], и соответствующий ему номер кластера.
1.2.3 Параметры алгоритма
- [math]\varepsilon[/math] — максимальное расстояние между соседями;
- [math]MinPts[/math] — минимальное количество элементов находящихся [math]\varepsilon[/math]-окрестности данного элемента для создания кластера.
1.2.4 Определения
- ядровой элемент: элемент [math]p[/math] является ядровым, если количество элементов в [math]\varepsilon[/math]-окрестности, включая сам элемент [math]p[/math] больше или равно [math]MinPts[/math];
- достижимость напрямую элемента [math]p[/math] из элемента q: элемент [math]p[/math] считается достижимым напрямую из элемента [math]q[/math], если элемент [math]q[/math] является ядровым, а элемент [math]p[/math] находится в [math]\varepsilon[/math]-окрестности элемента q;
- достижимость элемента [math]p[/math] из элемента [math]q[/math]: элемент [math]p[/math] достижим из элемента [math]q[/math], если существует путь [math]p_1, \dots, p_n[/math], где [math]p_1 = p[/math] и [math]p_n = q[/math], где [math]p_{i + 1}[/math] напрямую достижим из [math]p_{i}[/math];
- шум: все элементы, недостижимые из какого-либо другого считаются шумом.
Так как достижимость не является симметричным отношением (никакой элемент не может быть достижим из неядрового, вне зависимости от расстояния), то предлагается ввести следующее отношение:
- связанность элемента p и элемента q: элемент [math]p[/math] считается связанным с [math]q[/math], если существует такой элемент [math]o[/math], что [math]p[/math] и [math]q[/math] достижимы из него.
Таким образом кластер должен удовлетворять двум условиям:
- Все элементы внутри кластера взаимно связанны;
- Если элемент связан с каким-либо элементом кластера, то он тоже является частью кластера.

1.2.5 Пошаговое описание алгоритма
- Выбирается произвольная непосещенный элемент [math]p[/math].
- Элемент [math]p[/math] помечается как посещенный.
- Проверяется, является ли элемент [math]p[/math] ядровым.
- Если элемент [math]p[/math] является ядровым, то:
- Он становится началом нового кластера или сохраняет номер кластера, который был присвоен элементу ранее;
- Все элементы из [math]\varepsilon[/math]-окрестности элемента [math]p[/math] добавляются в его кластер (им присваевается номер кластера элемента [math]p[/math]);
- Процесс продолжается рекурсивно для каждого непосещенного элемента текущего кластера c шага 2.
- Если элемент [math]p[/math] не является ядровым, то [math]p[/math] объявляется шумом. Алгоритм продолжается с шага 4.
- Если элемент [math]p[/math] является ядровым, то:
- Если остались непосещенные точки, то алгоритм продолжается с шага 1.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является поиск элементов в [math]\varepsilon[/math]-окрестности каждого элемента входного множества [math]X[/math]. На эту часть алгоритма приходится основное время работы алгоритма, так как для каждого элемента необходимо выполнить эту операцию. Основные операции вычислительного ядра алгоритма: нахождение расстояние между элементами множества и сравнение его с порогом для определения того, являются ли один элемент достижимым напрямую из другого.
1.4 Макроструктура алгоритма
Алгоритм DBSCAN предполагает использование пространственной структуры данных (структуры, ориентированной на индексацию многомерной информации, такой как географические данные) — такие структуры позволяют найти все элементы в пределах определенного расстояния от текущего за [math]O(\log n)[/math]. Сложность построения таких структур [math]O(n \log n)[/math], таким образом, использование такой структуры не увеличивает сложность всего алгоритма.
1.5 Схема реализации последовательного алгоритма
[math]DBSCAN(X, \varepsilon, MinPts)[/math] [math]C = 0[/math] for [math]p[/math] in [math]X[/math]: if [math]p[/math] is [math]visited[/math]: # Skipping already visited elements continue mark [math]p[/math] as [math]visited[/math] # [Core operation] Searching for neighbors [math]neighbours[/math] = [math]\{ o \ | \ \forall o \in X: D(p, o) \le \varepsilon \}[/math] if [math]| neighbours | \ge MinPts[/math]: # Found new cluster [math]C = C + 1[/math] add [math]p[/math] to cluster [math]C[/math] # Looking for more neighbors, until none left for [math]q \in neighbours[/math]: if [math]q[/math] is not [math]visited[/math]: # If element is visited, then either it was marked as part of other cluster, or as noise mark [math]q[/math] as [math]visited[/math] # [Core operation] Searching for neighbors [math]q\_neighbours[/math] = [math]\{ o \ | \ \forall o \in X: D(q, o) \le \varepsilon \}[/math] if [math]| q\_neighbours | \ge MinPts[/math]: # We can expand neighbors with new elements from element [math]q[/math] [math]neighbours[/math] = [math]neighbours \cup q\_neighbours[/math] if [math]q[/math] has no cluster mark: # If it's noise — mark as edge-element part of cluster mark [math]q[/math] as part of cluster [math]C[/math] else: mark [math]p[/math] as [math]noise[/math]
1.6 Последовательная сложность алгоритма
Для того, чтобы проверить принадлежность элемента множества к кластеру необходимо получить список соседей в его [math]\varepsilon[/math]-окрестности. При использовании пространственной структуры данных данная операция может быть выполнена со сложностью [math]O(\log n)[/math]. Так как для необходимо определить принадлежность к кластеру всех элементов множества, то сложность самого алгоритма [math]O(n \log n)[/math]. При отказе от использования таких сткрутр сложность возрастает до [math]O(n^2)[/math], так как для каждого элемента требуется проверить на нахождение в [math]\varepsilon[/math]-окрестности все остальные элементы множества.
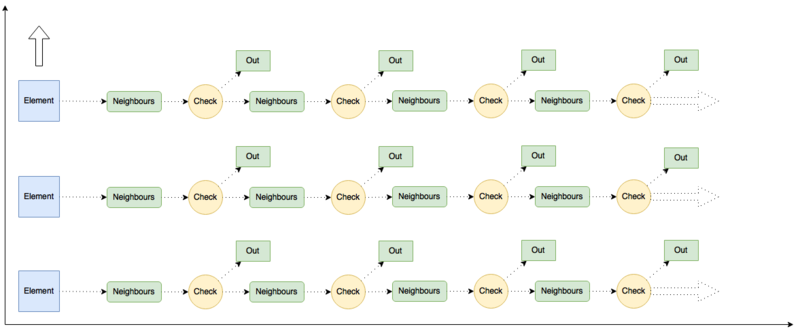
1.7 Информационный граф
Опишем граф алгоритма как аналитически, так и в виде рисунка:
Граф алгоритма состоит из двух групп вершин, расположенных узлах двух областей двумерной размерности.
Первой группе вершин соответствует операция Neighbours. Естественно введённые координаты области таковы:
- [math]i[/math] — меняется от [math]1[/math] до [math]k + f[/math], принимая все целочисленные значения, где [math]k[/math] — число результирующих кластеров, [math]f[/math] — число элементов помеченных, как шум
- [math]j[/math] — меняется от [math]1[/math] до [math]t[/math], принимая все целочисленные значения, где [math]t[/math] — число вершин в кластере [math]i[/math]
Второй группе вершин соответствует операция Check. Естественно введённые координаты области аналогичны предыдущей.
1.8 Ресурс параллелизма алгоритма
Так как в данном алгоритме присутствует параллелизм по данным, ширина ярусно-параллельной формы алгоритма [math]O(w)[/math], где [math]w[/math] — количество частей, на которые разбиваются все входное множество объектов [math]X[/math]. Высотой ярусно-параллельной формы алгоритма является [math]O(|H| \log |H|)[/math], где [math]|H|[/math] — максимальное количество элементов в области среди всех частей разбиения. Именно такую сложность имеет алгоритм PDBSCAN[3], применяемый к каждой отдельной части разбиения.
1.9 Входные и выходные данные алгоритма
Входные данные: множество [math]X[/math], на котором определена функция расстояния [math]D[/math].
Объём входных данных: [math]n[/math] (размерность входящего множества)
Выходные данные: размеченное множество точек [math]X[/math], в котором каждому элементу соответствует номер его кластера.
Объём выходных данных: [math]n[/math] (размерность выходящего множества)
1.10 Свойства алгоритма
Вычислительная мощность алгоритма (отношение числа операций к объему входных и выходных данных) является логарифмической.
- Алгоритм может определять кластера произвольной формы;
- Параллельная реализация при равномерном разбиении сбалансирована по количеству и виду производимых операций;
- Не требуется задание числа кластеров;
- Может выделять кластеры в присутствии шума;
- Не детерминирован относительно граничных точек кластеров.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- Параллельная реализация для Python на OpenMP/MPI
- Параллельная реализация для C++ на Boost и OpenMP с использованием VP-дерева
- Параллельная реализация для С++ на OpenMP с использованием системы непересекающихся множеств
- Параллельная реализация для многомерных данных для Python на SciPy и NumPy
- Последовательная реализация для R на С++
3 Литература
<references \> <references \>
<references \>
- ↑ A density-based algorithm for discovering clusters in large spatial database / M. Ester, H.-P. Kriegel, J. Sander, X. Xu // Proc. 1996 Intern. Conf. on Knowledge Discovery and Data Mining. – 1996.
- ↑ https://en.wikipedia.org/wiki/DBSCAN Density-based spatial clustering of applications with noise (DBSCAN)
- ↑ A New Scalable Parallel DBSCAN Algorithm Using the Disjoint-Set Data Structure \ Md. Mostofa Ali Patwary, Diana Palsetia, Ankit Agrawal, Wei-keng Liao, Fredrik Manne, Alok Choudhary