Участник:Bvdmitri/Адаптивное интегрирование

Основные авторы описания: Д.В.Багаев

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

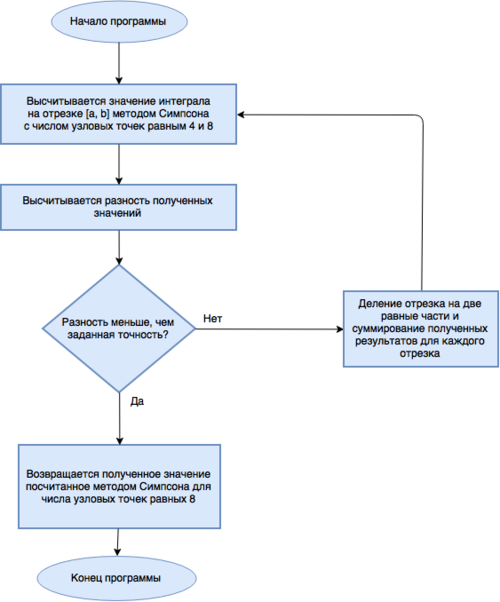
Адаптивное интегрирование — метод быстрого вычисления интеграла функции, который использует адаптивное изменение плотности сетки интегрирования. На промежутках, где функция гладкая, сетка разреженная, на промежутках со значительными колебаниями значений сетка гуще для получения необходимой точности.

1.2 Математическое описание алгоритма

Формулы метода:

1. Интеграл функции вычисляется по квадратурной формуле Симпсона с числом узловых точек равным 4 и 8 на отрезке [math][a, b] [/math].
2. Вычисляется разность найденных значений
   1. Если разность интегралов меньше либо равна желаемой точности интегрирования ε - заканчиваем процедуру.
   2. Если разность больше, то отрезок разбивается на два : [math][a, \tfrac{a + b} {2}][/math] и [math][\tfrac{a + b} {2}, b][/math] и для каждого отрезка повторяется процедура 1, затем возвращается сумма полученных значений.

Алгоритм имеет рекурсивную природу.

1.3 Вычислительное ядро алгоритма

Основное время работы алгоритма приходится на рекурсивные вызовы, а также на вычисление определенных интегралов методом Симпсона на отрезках, полученных в результате рекурсивного разбиения.

1.5 Схема реализации последовательного алгоритма

Простейшую рекурсивную реализацию данного алгоритма , которая не использует ресурсы параллелизма можно посмотреть здесь.

#include "SequentialMethod.h"

SequentialMethod::SequentialMethod(double eps, const std::function<double(double)> &f) : IntegrationMethod(eps, f) {}

double SequentialMethod::integrate(double a, double b) {
    double x = simpson(a, b, 4);
    double y = simpson(a, b, 8);
    if (fabs(x - y) < eps) {
        return y;
    } else {
        return integrate(a, (a + b) / 2.0) + integrate((a + b) / 2.0, b);
    }
}

SequentialMethod::~SequentialMethod() {}

1.6 Последовательная сложность алгоритма

Явную формулу сложности последовательного алгоритма выписать не представляется возможным, так как сложность зависит от структуры интегрируемой функции, длины отрезка, а так же необходимой точности.

1.7 Информационный граф

У алгоритма есть несколько возможностей для распараллеливания.
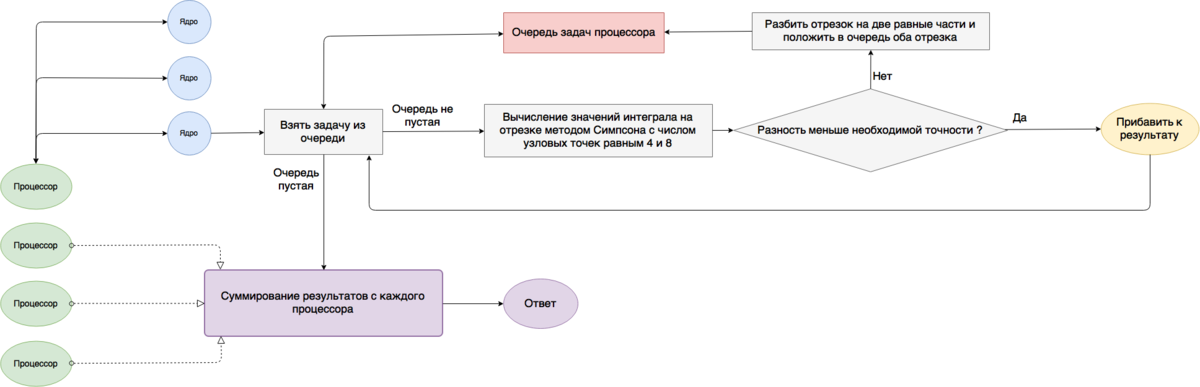
В первом случае можно разбить отрезок на фиксированное число подотрезков, и каждый подотрезок считать на одном процессоре с дальнейшим суммированием результатов с каждого процессора. Внутри процессора используется схема очереди задач. Рекурсия заменяется на операции добавить и достать задачу из общей очереди задач.

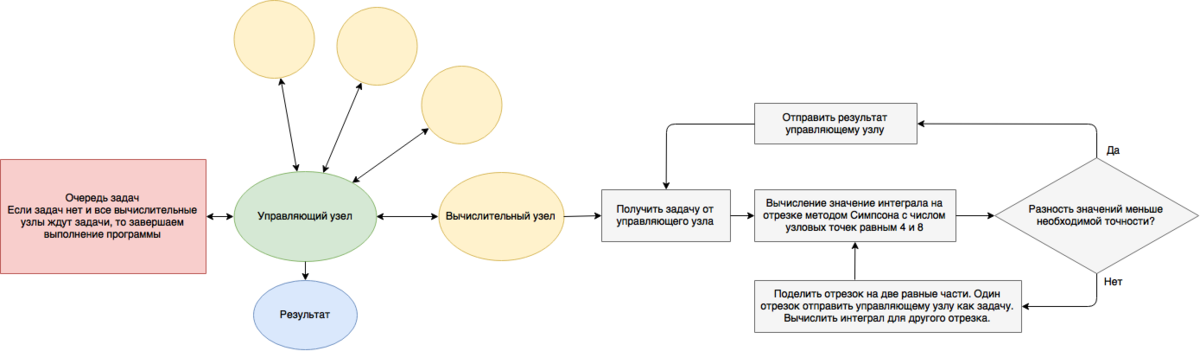
Во втором случае можно использовать управляющий узел для распределения задач между вычислительными узлами. В данном случае можно избежать ситуации, когда интегрируемая функция сильно осциллирует лишь на небольшом участке отрезка и большинство процессоров завершают свою работу раньше и ждут остальных.

1.8 Ресурс параллелизма алгоритма

Исходную задачу можно разбить на более мелкие задачи делением отрезка. Каждая задача может быть решаться отдельно от остальных, за счет чего можно достичь высокой масштабируемости.

1.9 Входные и выходные данные алгоритма

1.9.1 Входные данные

• Функция.
• Отрезок интегрирования [math][a, b][/math].
• Желаемая точность интегрирования [math]\varepsilon[/math].

1.9.2 Выходные данные

• Определенный интеграл функции на отрезке [a, b] с точностью ε.

1.10 Свойства алгоритма

• Алгоритм устроен таким образом, что шаг сетки необходимой для вычисления определенного интеграла с заданной точностью адаптируется под сложность функции.
• Алгоритм является устойчивым
• Алгоритм является детерминированным

2 Программная реализация алгоритма

2.3 Возможные способы и особенности параллельной реализации алгоритма

Алгоритм имеет несколько возможных параллельных реализаций.

2.3.1 Очередь задач на общей памяти

Реализация для эффективного использования многомерного процессора. В данном случае вместо рекурсии используется очередь задач общая для всех ядер процессора.

Плюсы данного подхода:

• Очень простая реализация

Минусы данного подхода:

• Нет возможности использовать многопроцессорные кластеры, так как очередь задач находится в общей памяти.
• Масштабируемость достигается только при увеличении количества ядер в одном процессоре.

2.3.2 Деление на подотрезки

Отрезок интегрирования делится на одинаковые по длине отрезки. Количество этих отрезков определяется числом доступных процессоров. Каждый процессор считает определенный интеграл лишь на своем отрезке используя внутри себя очередь задач в общей памяти.

Плюсы данного подхода:

• Хорошая масштабируемость на большом классе функций

Минусы данного подхода:

• Отсутсвие балансировки нагрузки; разброс нагрузок на процессоры может оказаться значительным, что приведет к простою части ядер.

2.3.3 Использование управляющего узла

Можно использовать управляющий узел, который будет распределять нагрузку между вычислительными узлами.

Плюсы данного подхода:

• Балансировка нагрузки

Минусы данного подхода:

• Более сложная реализация
• Хорошая масштабируемость достигается на очень узком классе функций
• Плохая масштабируемость при очень большом количестве вычислительных узлов, управляющий узел перестает успевать распределять задачи из-за чего большое количество вычислительных узлов простаивают

2.4 Масштабируемость алгоритма и его реализации

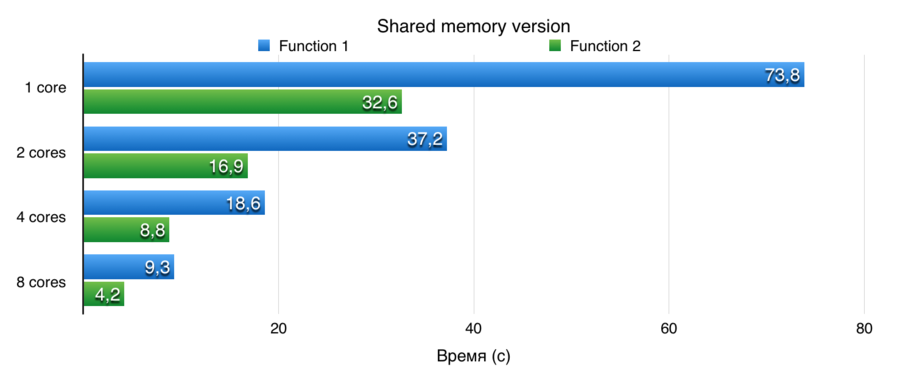
Для тестирования масштабируемости были проведены серии тестов с различными функциями. Функции и отрезки интегрирования выбирались таким образом, чтобы первоначальное время вычисление интеграла на последовательной версии было существенно большим. Далее проводились замеры времени для каждой реализации. Количество ядер выбиралось равным степени двойки, а также исходя из специфики самой реализации.

Все тесты проводились на суперкомпьютере Ломоносов. Характеристики вычислительного кластера: link.

2.4.1 Очередь задач на общей памяти

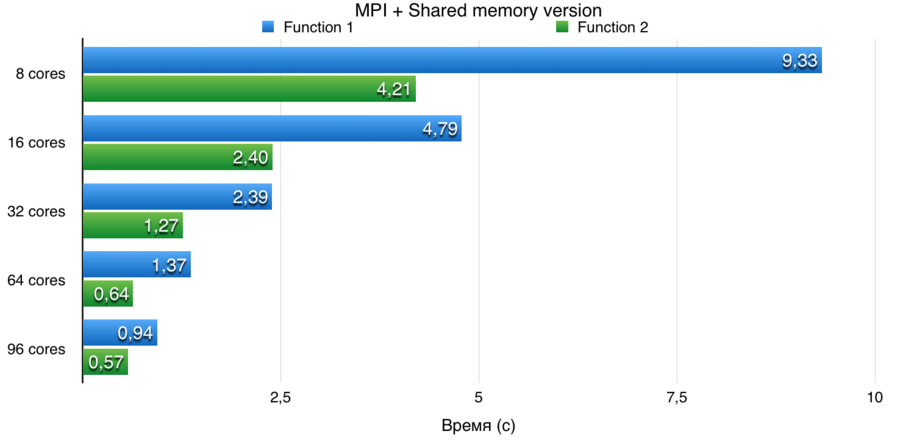
Данная реализация показывает практически линейную масштабируемость, но из-за использования для параллельности только общей памяти процессора, максимальное количество вычислительных единиц ограничено количеством ядер в одном процессоре.

2.4.1.1 Исходный код

GitHub

#include "TBBMethod.h"

TBBMethod::TBBMethod(double eps, const std::function<double(double)> &f) : IntegrationMethod(eps, f) {}

double TBBMethod::integrate(double a, double b) {
    double x = simpson(a, b, 4);
    double y = simpson(a, b, 8);
    if (fabs(x - y) < eps) {
        return y;
    } else {
        tbb::task_group group;

        group.run([&] {
            x = integrate(a, (a + b) / 2.0);
        });

        group.run_and_wait([&] {
            y = integrate((a + b) / 2.0, b);
        });

        return x + y;
    }
}

TBBMethod::~TBBMethod() {}

2.4.2 Деление на подотрезки

Данная реализация практически всегда показывает линейную масштабируемость.

2.4.2.1 Исходный код

GitHub

#include "MPI_TBBMethod.h"

MPI_TBBMethod::MPI_TBBMethod(double eps, const std::function<double(double)> &f) : IntegrationMethod(eps, f) {}

double MPI_TBBMethod::tbb_run(double a, double b) {
	double x = simpson(a, b, 4);
    double y = simpson(a, b, 8);
    if (fabs(x - y) < eps) {
        return y;
    } else {
        tbb::task_group group;

        group.run([&] {
            x = tbb_run(a, (a + b) / 2.0);
        });

        group.run_and_wait([&] {
            y = tbb_run((a + b) / 2.0, b);
        });

        return x + y;
    }
}

double MPI_TBBMethod::integrate(double a, double b) {
    double answer = 0.0;
    int nodes = 1;
    MPI_Comm_size(MPI_COMM_WORLD, &nodes);

    int node_id = 0;
    MPI_Comm_rank(MPI_COMM_WORLD, &node_id);

    double h = (b - a) / (double) nodes;

    a = a + h * node_id;
    b = a + h;

    double node_answer = tbb_run(a, b);
    MPI_Barrier(MPI_COMM_WORLD);
    if (node_id == 0) {
    	answer += node_answer;
        for (int i = 1; i < nodes; i++) {
            MPI_Recv(&node_answer, 1, MPI_DOUBLE, MPI_ANY_SOURCE, MPI_ANY_TAG, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
            answer += node_answer;
        }
    } else {
        MPI_Send(&node_answer, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
    }

    MPI_Barrier(MPI_COMM_WORLD);

	return answer;
}

MPI_TBBMethod::~MPI_TBBMethod() {}

2.4.3 Использование управляющего узла

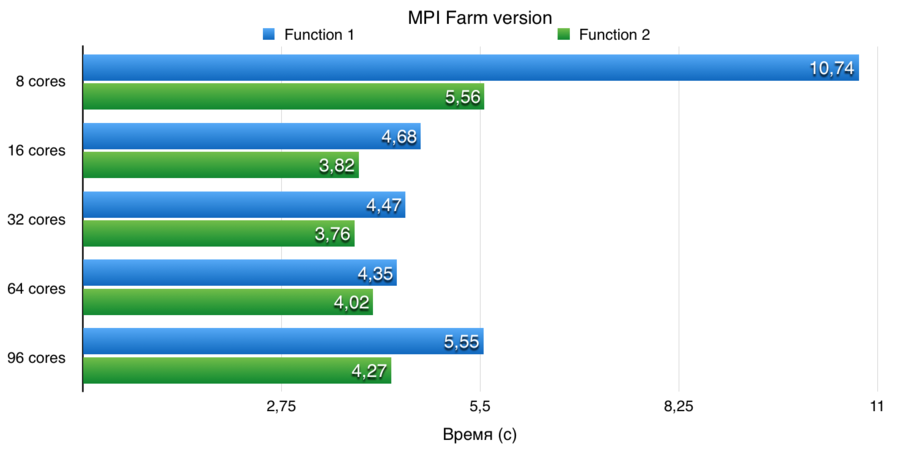
Данная реализация показывает плохую масштабируемость при очень большом количестве вычислительных узлов, управляющий узел перестает успевать распределять задачи из-за чего большое количество вычислительных узлов простаивают

2.4.3.1 Исходный код

GitHub.

Исходный код для управляющего узла.

#include "Farm.h"

Farm::Farm(int nodes_num, double a, double b, double tau) {
    this->nodes_num = nodes_num;
    this->availableNodes = (int *) calloc((size_t) nodes_num, sizeof(int));
    this->availableNodesCount = nodes_num - 1;
    this->a = a;
    this->b = b;
    this->tau = tau;
    this->answer = 0.0;


    this->jobCount = 0;
    this->jobs = (double *) calloc(FARM_JOBS_BUFFER_SIZE, sizeof(double));
    //Buf structure
    //0 - a
    //1 - b
    //2 - tau, if tau < 0, a = y or exit job

    this->message_buffer = (double *) calloc(FARM_MPI_BUFFER_SIZE, sizeof(double));
    MPI_Buffer_attach(message_buffer, FARM_MPI_BUFFER_SIZE * sizeof(double));
    //Main node is always busy
    availableNodes[0] = 1;
}

void Farm::SendInitialJobs() {
    double shift = (b - a) / (nodes_num - 1);
    double *buf = (double *) calloc(3, sizeof(double));
    for (int i = 0; i < nodes_num - 1; i++) {
        buf[0] = a + shift * i;
        buf[1] = buf[0] + shift;
        buf[2] = tau;

        MPI_Bsend(buf, 3, MPI_DOUBLE, i + 1, JOB_SEND_TAG, MPI_COMM_WORLD);
        availableNodes[i + 1] = 1;
        availableNodesCount -= 1;
    }
}

void Farm::work() {
    double buf[3];
    MPI_Status status;
    while (true) {
        MPI_Recv(buf, 3, MPI_DOUBLE, MPI_ANY_SOURCE, JOB_SAVE_OR_RESULT_TAG, MPI_COMM_WORLD, &status);
        int source = status.MPI_SOURCE;

        if (buf[2] < 0.0) {
            //Node send result
            answer += buf[0];
            if (jobCount != 0) {
                buf[0] = jobs[(jobCount - 1) * 3 + 0];
                buf[1] = jobs[(jobCount - 1) * 3 + 1];
                buf[2] = jobs[(jobCount - 1) * 3 + 2];
                jobCount -= 1;

                MPI_Bsend(buf, 3, MPI_DOUBLE, source, JOB_SEND_TAG, MPI_COMM_WORLD);
            } else {
                availableNodes[source] = 0;
                availableNodesCount += 1;
                if (availableNodesCount == (nodes_num - 1)) {
                    KillWorkers();
                    break;
                }
            }
        } else {
            //Node send job
            if (availableNodesCount != 0) {
                for (int i = 1; i < nodes_num; i++) {
                    if (availableNodes[i] == 0) {
                        MPI_Bsend(buf, 3, MPI_DOUBLE, i, JOB_SEND_TAG, MPI_COMM_WORLD);
                        availableNodes[i] = 1;
                        availableNodesCount -= 1;
                        break;
                    }
                }
            } else {
                jobs[jobCount * 3 + 0] = buf[0];
                jobs[jobCount * 3 + 1] = buf[1];
                jobs[jobCount * 3 + 2] = buf[2];
                jobCount += 1;
            }
        }

    }
}

void Farm::KillWorkers() {
    double buf[3];
    buf[2] = -1.0;
    for (int i = 1; i < nodes_num; i++) {
        MPI_Bsend(buf, 3, MPI_DOUBLE, i, JOB_SEND_TAG, MPI_COMM_WORLD);
    }
}

double Farm::Result() {
    return answer;
}

Farm::~Farm() {
    free(jobs);
    int size = FARM_MPI_BUFFER_SIZE * sizeof(double);
    MPI_Buffer_detach(message_buffer, &size);
    free(message_buffer);
}

Исходный код для вычислительных узлов.

#include <cmath>
#include "Worker.h"

Worker::Worker(const std::function<double(double)> &f): f(f) {
    this->buf = (double *) calloc(16, sizeof(double));
    this->message_buffer = (double *) calloc(WORKER_MPI_BUFFER_SIZE, sizeof(double));
    MPI_Buffer_attach(message_buffer, WORKER_MPI_BUFFER_SIZE * sizeof(double));
}

void Worker::work() {
    while (true) {
        GetJob();
        if (buf[2] > 0.0) {
            Calculate();
        } else {
            break;
        }
    }
}

void Worker::GetJob() {
    MPI_Recv(buf, 3, MPI_DOUBLE, 0, JOB_GET_TAG, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}

void Worker::Calculate() {
    double a = buf[0];
    double b = buf[1];
    double tau = buf[2];

    while (true) {
        double x = simpson(a, b, 4);
        double y = simpson(a, b, 8);

        if (fabs(x - y) < tau) {
            SendResult(y);
            break;
        } else {
            SaveJob(a, (a + b) / 2, tau / 2);
            a = (a + b) / 2;
            tau = tau / 2;
        }

    }
}

void Worker::SaveJob(double a, double b, double tau) {
    double job[3];
    job[0] = a;
    job[1] = b;
    job[2] = tau;
    MPI_Bsend(job, 3, MPI_DOUBLE, 0, JOB_SAVE_OR_RESULT_TAG, MPI_COMM_WORLD);
}

void Worker::SendResult(double result) {
    double r[3];
    r[0] = result;
    r[1] = 0.0;
    r[2] = -1.0;
    MPI_Bsend(r, 3, MPI_DOUBLE, 0, JOB_SAVE_OR_RESULT_TAG, MPI_COMM_WORLD);
}

Worker::~Worker() {
    free(buf);
    int size = WORKER_MPI_BUFFER_SIZE * sizeof(double);
    MPI_Buffer_detach(message_buffer, &size);
    free(message_buffer);
}


double Worker::simpson(double a, double b, int k) {
    double h = (b - a) / ((double) 2 * k);
    double answer = 0.0;
    for (int j = 1; j < 2 * k; j += 2) {
        answer += (f(a + h * (j - 1)) + 4 * f(a + h * j) +
                   f(a + h * (j + 1)));
    }
    return h * answer / 3;
}

2.7 Существующие реализации алгоритма

• Adaptive Simpson's method
• Якобовский М.В., Кулькова Е.Ю. "Решение задач на многопроцессорных вычислительных системах с разделяемой памятью."

3 Литература

• Adaptive Quadrature Wikipedia
• Simpson's Rule
• Якобовский М.В., Кулькова Е.Ю. "Решение задач на многопроцессорных вычислительных системах с разделяемой памятью."