Участник:Vlamakarenko/Трассировка лучей: различия между версиями
| Строка 51: | Строка 51: | ||
Энергетическую яркость, падающую на элемент поверхности, будем назвать '''падающей яркостью'''. Энергетическую яркость, испускаемую элементом поверхности, будем называть '''излучаемой яркостью'''. | Энергетическую яркость, падающую на элемент поверхности, будем назвать '''падающей яркостью'''. Энергетическую яркость, испускаемую элементом поверхности, будем называть '''излучаемой яркостью'''. | ||
| + | |||
| + | Из определений следует, что: | ||
| + | |||
| + | 1) <math>dE_i(\overline{p}, \overline{\omega}_i) = L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i \, d\omega_i</math> <br> | ||
| + | 2) <math>E(\overline{p}) = \int_{\Omega_i} L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i \, d\omega_i</math>, где интегрирование проводится по направлениям <math>\overline{w}_i</math> таким, что <math>(\overline{n}, \overline{w}_i)</math> > 0, то есть по полусфере.<br> (<math>\overline{n}</math> - нормаль к поверхности в точке <math>\overline{p}</math>). | ||
| + | |||
Пусть в точке <math>p</math> некоторой поверхности заданы два вектора: <math>w_i, w_o</math>. | Пусть в точке <math>p</math> некоторой поверхности заданы два вектора: <math>w_i, w_o</math>. | ||
Версия 23:28, 19 ноября 2016
авторы: В.А.Макаренко, Р.А.Габдуллин
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
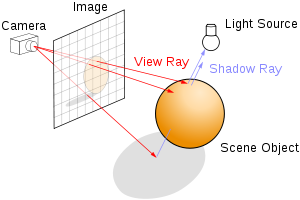
Трассировка лучей - это технология визуализации трехмерных сцен путем отслеживания обратной траектории лучей света (от наблюдателя к источнику). Достоинствами данного метода являются реалистичность итоговых изображений, возможность визуализации гладких объектов без аппроксимации полигональными поверхностями, простота реализации отражений, преломлений, взятия в фокус, реалистичного освещения; возможность параллельной обработки лучей.
1.2 Математическое описание алгоритма
1.2.1 Основные определения
Объект - поверхность в трехмерном пространстве.
Сцена - четверка {камера, объекты, источники света, видовая плоскость}.
1.2.1.1 Камера
Камера - "виртуальный глаз", через который мы видим объекты сцены.
Камера задается положением в пространстве и ортонормированным базисом [math](\overline{u}_c, \overline{v}_c, \overline{w}_c)[/math] (локальная система координат). [math]\overline{u}_c[/math] направлен вправо относительно наблюдателя, [math]\overline{v}_c[/math] - вверх, [math]\overline{w}_c[/math] - на наблюдателя. Таким образом, [math](\overline{u}_c, \overline{v}_c, \overline{w}_c)[/math] - правая тройка векторов. Вектор направления камеры в своей системе координат: [math](0, 0, -1)[/math].
1.2.1.2 Видовая плоскость
Перед камерой на расстоянии [math]d[/math] поставим пиксельную сетку [math]w \times h[/math] с размером пикселя [math]s \times s[/math] так, чтобы камера была направлена в ее центр. Итоговое изображение будет получено из этой сетки покраской пикселей в нужный цвет.
[math]p(i, j)[/math], где [math]i=\overline{0,h-1}, \quad j=\overline{0,w-1}[/math] - пиксел [math]i[/math]-ой строки снизу [math]j[/math]-го столбца слева.
Заметим, что с увеличением [math]d[/math] уменьшается угол обзора, а [math]s[/math] влияет на масштаб.
1.2.1.3 Определения из радиометрии
Энергия излучения - энергия, переносимая оптическим излучением. Обозначается через [math]Q[/math].
Поток излучения - мощность, переносимая оптическим излучением через какую-либо поверхность. [math]\Phi = \frac{dQ}{dt}[/math].
Плотность потока излучения - отношение потока излучения, проходящего через малый участок поверхности, к площади этой поверхности. [math]\frac{d\Phi}{dA}[/math], где [math]dA[/math] - дифференциал поверхности.
Облученность - отношение потока излучения, падающего на малый участок поверхности, к площади этой поверхности. [math]E=\frac{d\Phi}{dA}[/math], где [math]dA[/math] - дифференциал поверхности.
Энергетическая светимость - отношение потока излучения, испускаемого малым участком поверхности, к площади этой поверхности. [math]M=\frac{d\Phi}{dA}[/math], где [math]dA[/math] - дифференциал поверхности.
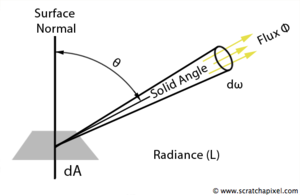
Сила излучения - мощность, переносимая излучением в некотором направлении. Равна отношению потока излучения, исходящего от источника, к малому телесному углу. [math]I=\frac{d\Phi}{d\omega}[/math].
Энергетическая яркость - отношение потока излучения через малую площадку поверхности и распространяющегося в малом телесном угле, к площади проекции этой площадки на плоскость, перпендикулярную направлению распространения, и величине телесного угла. [math]L=\frac{d^2\Phi}{dA\cdot d\omega \cdot \cos \theta}[/math]
Энергетическую яркость, падающую на элемент поверхности, будем назвать падающей яркостью. Энергетическую яркость, испускаемую элементом поверхности, будем называть излучаемой яркостью.
Из определений следует, что:
1) [math]dE_i(\overline{p}, \overline{\omega}_i) = L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i \, d\omega_i[/math]
2) [math]E(\overline{p}) = \int_{\Omega_i} L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i \, d\omega_i[/math], где интегрирование проводится по направлениям [math]\overline{w}_i[/math] таким, что [math](\overline{n}, \overline{w}_i)[/math] > 0, то есть по полусфере.
([math]\overline{n}[/math] - нормаль к поверхности в точке [math]\overline{p}[/math]).
Пусть в точке [math]p[/math] некоторой поверхности заданы два вектора: [math]w_i, w_o[/math].
1.2.1.4 Источники света
Типы источников света:
1) Point light - точка, излучающая свет одиноково во всех направлениях.
2) Directional light - бесконечно удаленный источник света, задается направлением.
3) Area light - объект, излучающий свет одинаково во всех направлениях.
1.2.2 Входные данные
[math]scene = \{objects, lights, camera\}[/math] - сцена, которая будет визуализирована алгоритмом, где
[math]objects[/math] - множество объектов (например сфера, плоскость, треугольник, составной объект и т. п.).
[math]lights[/math] - множество источников света (точечные источники, направленные источники, светящиеся объекты)
[math]camera[/math] - камера наблюдения ("виртуальный глаз").
Объекты задаются произвольным образом так, чтобы можно было найти пересечение луча с этим объектом (например, для сферы достаточно задать положение в пространстве и радиус, а для плоскости - точку, принадлежащую ей и нормаль). Также, для каждого объекта необходимо задать материал - информацию о его отражающих, преломляющих, поглощающих свойствах.
Источники света задаются по-разному, в зависимости от способа распространения света от источника. Например, точечные источники света задаются положением в пространстве и интенсивностью, направленные - интенсивностью и вектором направления.
Камера задается положением в пространстве и ортонормированным базисом [math](\overline{u}_c, \overline{v}_c, \overline{w}_c)[/math] (локальная система координат). [math]\overline{u}_c[/math] направлен вправо относительно наблюдателя, [math]\overline{v}_c[/math] - вверх, [math]\overline{w}_c[/math] - на наблюдателя. Таким образом, [math](\overline{u}_c, \overline{v}_c, \overline{w}_c)[/math] - правая тройка векторов. Вектор направления камеры в своей системе координат: [math](0, 0, -1)[/math].
1.2.3 Генерация луча
Перед камерой на расстоянии [math]d[/math] поставим пиксельную сетку [math]w \times h[/math] с размером пикселя [math]s \times s[/math] так, чтобы камера была направлена в центр сетки. Итоговое изображение будет получено из этой сетки покраской пикселей в нужный цвет.
Пусть [math]p(i, j)[/math], где [math]i=\overline{0,h-1}, \quad j=\overline{0,w-1}[/math] - пиксел [math]i[/math]-ой строки снизу [math]j[/math]-го столбца слева. Проведем луч из камеры к центру пикселя в локальной системе координат камеры. Начало луча в точке [math]\overline{pos}=(0,0,0)[/math]. Найдем вектор направления [math]\overline{dir}[/math]:
[math]\overline{dir}.x = s (j -\frac{w}{2} + \frac{1}{2}) [/math]
[math]\overline{dir}.y = s (i -\frac{h}{2} + \frac{1}{2}) [/math]
[math]\overline{dir}.z = d[/math]
Нормируем вектор [math]\overline{dir}[/math] и переведем луч в глобальную систему координат.
1.2.4 Пересечение луча с объектами сцены
Все точки луча [math]ray(\overline{p}, \overline{d})[/math] можно представить в виде:
[math]h(x,y,z)=\overline{p}+t \cdot \overline{d}, \quad t \in [0;\infty) [/math].
Луч пересекает объект [math]O_i[/math] тогда и только тогда, когда [math]t_i = \inf\{t \gt 0 \, | \quad \overline{p}+t \cdot \overline{d} \in O_i\} \, \lt \infty[/math]
Если луч пересекает объект [math]O_i[/math], то [math]h_i(x,y,z) = \overline{p}+t_i \cdot \overline{d}[/math] - их первое пересечение, [math]t_i[/math] - расстояние от начала луча до точки пересечения.
1.2.5 Вычисление цвета в точке пересечения
Найдем [math]T = \{t_i\}[/math] - параметры пересечения с объектами (см. предыдущий пункт).
[math]t_{min} = \min \{t_i\}, \quad O_{min} = \{O_i | t_i = t_{min}\}[/math]
Если [math]t_{min} = \infty[/math], то луч не пересекает ни один объект и нужно покрасить соответствующий пиксел в черный цвет (цвет фона).
Если [math]t_{min} \lt \infty[/math], то нужно найти выходящее излучение (цвет) из точки пересечения в камеру. Выходящее излучение зависит от свойств материала объекта, прямого (излучение, исходящее от источников света) и непрямого (отраженный свет) излучений, входящих в точку пересечения; угла между нормалью к поверхности в точке пересечения и направлением луча.
1.2.6 Вычисление прямого излучения
[math]h_{min}(x,y,z) = \overline{p}+t_{min} \cdot \overline{d}[/math].
[math]L_{is} = \sum_i L(S_i, h_{min})[/math] - прямое входящее излучение.
[math]L(S_i, h_{min})[/math] - излучение источника света [math]S_i[/math], приходящее в точку [math]h_{min}[/math].
Суммирование ведется по [math]i[/math] таким, что [math]S_i[/math] "виден" из точки [math]h_{min}[/math], в противном случае какой-то объект загораживает источник света, и в точку [math]h_{min}[/math] будет падать тень от этого объекта.
1.2.7 Вычисление непрямого излучения
Рассмотрим упрощенную модель непрямого излучения. Пусть материал объекта [math]O_{min}[/math] обладает способностью отражать свет.
Тогда нужно найти излучение, приходящее со стороны отраженного луча:
[math]ray(\overline{h}_{min}, \overline{w}_i)[/math] - отраженный луч.
[math]\overline{w}_i = \overline{d} -2\cdot (\overline{n}, \overline{d})\cdot \overline{n}[/math].
[math]L\{ray(\overline{h}_{min}, \overline{w}_i)\}[/math] - излучение приходящее со стороны отраженного луча. Оно находится тем же самым алгоритмом, что и цвет пикселя (то есть рекурсивно).
1.2.8 Улучшение визуальных качеств изображения
Чтобы сгладить изображение и избавиться от шума, обычно через пиксел проводят не один луч, а достаточно много лучей, для каждого считают цвет, а потом усредняют по всем лучам (берут среднее арифметическое).
1.3 Вычислительное ядро алгоритма
Основные вычисления связаны с:
1) поиском пересечения луча с объектами сцены.
2) расчетом излучения от каждого источника света (требуется определить, "виден" ли источник света из точки пересечения с объектом).
1.4 Макроструктура алгоритма
Для каждого пикселя изображения генерируется пучок лучей, проходящих через этот пиксел. Для каждого луча находится первое пересечение с объектами сцены, расчитывается прямое и непрямое входящие излучения и итоговое выходящее. После этого цвет усредняется по всем лучам данного пикселя.
1.5 Схема реализации последовательного алгоритма
Здесь приведен псевдокод ключевых моментов алгоритма.
//Покраска пикселей изображения
for (uint r = 0; r < h; r++) //строки
{
for (uint c = 0; c < w; c++) //столбцы
{
image(r,c) = renderPixel(r, c); //вычисляем цвет в пикселе
}
}
//renderPixel(r, c)
pixel_color = {0,0,0};
for (uint j = 0; j < num_rays_per_pixel; j++)
{
pp = generatePoint(); //генерируем произвольное смещение внутри пикеля
//вычисляем координаты точки на полотне
x = s * (c - 0.5 * w + pp.x);
y = s * (r - 0.5 * h + pp.y);
//cоздаем луч
Ray ray({0,0,0}, normalize({x,y,-d}));
Ray worldRay = convertToWorldCoords(ray);
pixel_color += traceRay(worldRay, 0) * 1.0 / num_rays_per_pixel; //вычисляем цвет для каждого луча и усредняем
}
//traceRay(ray, depth)
if (depth > max_depth) //превысили максимальную глубину луча, дальше не идем
{
return black; //возвращаем черный цвет
}
Intersection is = hitObjects(ray); //нашли первое пересечение с объектами сцены и записали информацию о нем в is:
//материал объекта, расстояние, нормаль и т. п.
if (is) //если есть пересечение
{
is.ray = ray; //запомнили луч
is.depth = depth; // и глубину
return shade(is); //расчитали цвет в точке пересечения в зависимости
//от материала объекта, используя информацию о пересечении
}
return getBackgroundColor(ray); //вернули цвет фона
//shade(is)
//цвета
direct_illumination = {0,0,0};
indirect_illumintaion = {0,0,0};
for (uint i = 0; i < light_count; i++)
{
if (light[i].isVisible(is)) //если источник света виден из точки пересечения
{
direct_illumination = getIllumination(light[i], is); //рассчитываем прямое излучение от i-го источника света
}
}
if (isReflective(is.object))
{
indirect_illumination = traceRay(reflecedRay(is.ray), is.depth + 1);
}
//зная входящее излучение, расчитываем выходящее в зависимости от свойств материала объекта
//...
1.6 Последовательная сложность алгоритма
[math]w[/math] - ширина полотна
[math]h[/math] - высота полотна
[math]depth_{max}[/math] - максимальная глубина луча в рекурсии (помимо первичного луча)
[math]N_{obj}[/math] - количество объектов сцены
[math]N_{lights}[/math] - количество источников света сцены
[math]N_{rays}[/math] - число лучей на один пиксел
На каждой итерации ищется пересечение луча со всеми объектами: [math]O(N_{obj})[/math]
После нахождения точки пересечения, выясняется, виден ли каждый источник света из этой точки. Для этого нужно найти первое пересечение теневого луча (начало в точке пересечения, направлен к источнику света) и сравнить расстояние до точки пересечения с расстоянием до источника света. Для всего этого требуется [math]O(N_{lights} \cdot N_{obj})[/math] операций.
Для каждого луча понадобится [math]O(depth_{max}(N_{obj} + N_{obj} \cdot N_{lights})) = O(depth_{max}\cdot N_{obj} \cdot N_{lights})[/math] операций.
Всего лучей, выходящих из камеры [math]w \cdot h \cdot N_{rays}[/math].
В итоге получаем [math]O(depth_{max}\cdot N_{obj} \cdot N_{lights} \cdot w \cdot h \cdot N_{rays})[/math] операций.
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
RenderMan
V-Ray
NVIDIA IRay
NVIDIA mental ray
Hydra Renderer