Участник:Максим

Метод Рунге-Кутты четвертого порядка решения системы линейных дифференциальных уравнений

Метод Рунге-Кутты четвертого порядка решения системы линейных дифференциальных уравнений

Автором статьи является Амбарцумян М.Е.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Ме́тод Ру́нге — Ку́тты 4-го порядка — важный итерационный метод численного решения систем обыкновенных дифференциальных уравнений. Он был разработан около 1900 года немецкими математиками К. Рунге и М. В. Куттой. Для численного решения системы на отрезке, на котором определена независимая переменная, задается сетка с некоторым маленьким шагом. Последовательно, на каждом шаге, вычисляем значения зависимых переменных через значения зависимых переменных на предыдущем шаге по формулам Рунге-Кутты.

1.2 Математическое описание алгоритма

Рассматривается следующая система ОДУ:

[math] \begin{align} X^'=f(t,X,Y,...)\\ Y^'=g(t,X,Y,...),... \end{align} [/math]

и т.д.

с начальным условием [math] X(t_0)=X_0,Y(t_0)=Y_0,... [/math]

Пусть h-шаг сетки, тогда имеем следующие формулы Рунге-Кутты численного решения системы:

[math] \begin{align} t_{k+1}=t_{k}+h\\ X_{k+1}=\frac{1}{6}(k_1+2k_2+2k_3+k_4),\\ Y_{k+1}=\frac{1}{6}(m_1+2m_2+2m_3+m_4),...,\\ k_1=f(t_k,X_k,Y_k,...)h,\\ m_1=g(t_k,X_k,Y_k,...)h,...,\\ k_2=f(t_k+\frac{h}{2},X_k+\frac{k_1}{2},Y_k+\frac{m_1}{2},...)h,\\ m_2=g(t_k+\frac{h}{2},X_k+\frac{k_1}{2},Y_k+\frac{m_1}{2},...)h,...,\\ k_3=f(t_k+\frac{h}{2},X_k+\frac{k_2}{2},Y_k+\frac{m_2}{2},...)h,\\ m_3=g(t_k+\frac{h}{2},X_k+\frac{k_2}{2},Y_k+\frac{m_2}{2},...)h,...,\\ k_4=f(t_k+h,X_k+k_3,Y_k+m_3,...)h,\\ m_4=g(t_k+h,X_k+k_3,Y_k+m_3,...)h,...\\ \end{align} [/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро метода Рунге-Кутты можно составить из множественных вычислений функций f,g,... и т.д.

1.4 Макроструктура алгоритма

На макроуровне алгоритм представляет из себя многократное вычисление функций f,g и т.д. на каждом шаге сетки. То есть на одном шаге для каждой зависимой переменной вычисляется 4 раза многомерная функция, чтобы найти коэффициенты, через которые находится очередное значение зависимой переменной на данной итерации.

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

[math] 1. t_{k+1}=t_{k}+h [/math]

[math] 2. k_1=f(t_k,X_k,Y_k,...)h,[/math]

[math]   m_1=g(t_k,X_k,Y_k,...)h,...,[/math]

[math]  k_2=f(t_k+\frac{h}{2},X_k+\frac{k_1}{2},Y_k+\frac{m_1}{2},...)h,[/math]

[math]  m_2=g(t_k+\frac{h}{2},X_k+\frac{k_1}{2},Y_k+\frac{m_1}{2},...)h,...,[/math]

[math]  k_3=f(t_k+\frac{h}{2},X_k+\frac{k_2}{2},Y_k+\frac{m_2}{2},...)h,[/math]

[math]   m_3=g(t_k+\frac{h}{2},X_k+\frac{k_2}{2},Y_k+\frac{m_2}{2},...)h,...,[/math]

[math]  k_4=f(t_k+h,X_k+k_3,Y_k+m_3,...)h,[/math]

[math]  m_4=g(t_k+h,X_k+k_3,Y_k+m_3,...)h,...[/math]

[math] 3. X_{k+1}=\frac{1}{6}(k_1+2k_2+2k_3+k_4),[/math]

[math] Y_{k+1}=\frac{1}{6}(m_1+2m_2+2m_3+m_4),...[/math]

Приведенные выше шаги выполняются в цикле m раз, где m-размер сетки. На первом шаге вычисляется очередная точка на сетке. На втором шаге считаются необходимые коэффициенты метода Рунге-Кутты для каждой зависимой переменной (4 коэффициента для каждой переменной). На третьем шаге получаем значения зависимых переменных на очередной итерации.

1.6 Последовательная сложность алгоритма

Пусть m-число узлов сетки, n-размерность системы ОДУ. Тогда найдем количество операций, требуемое для решения задачи.

Общая последовательная сложность алгоритма О(nm)

1. Сложений

[math] (7n+2)m [/math]

2. Умножений

[math] 4nm [/math]

3. Делений

[math] (4n+1)m [/math]

4. Вычислений значения многомерной функции

[math] 4nm [/math]

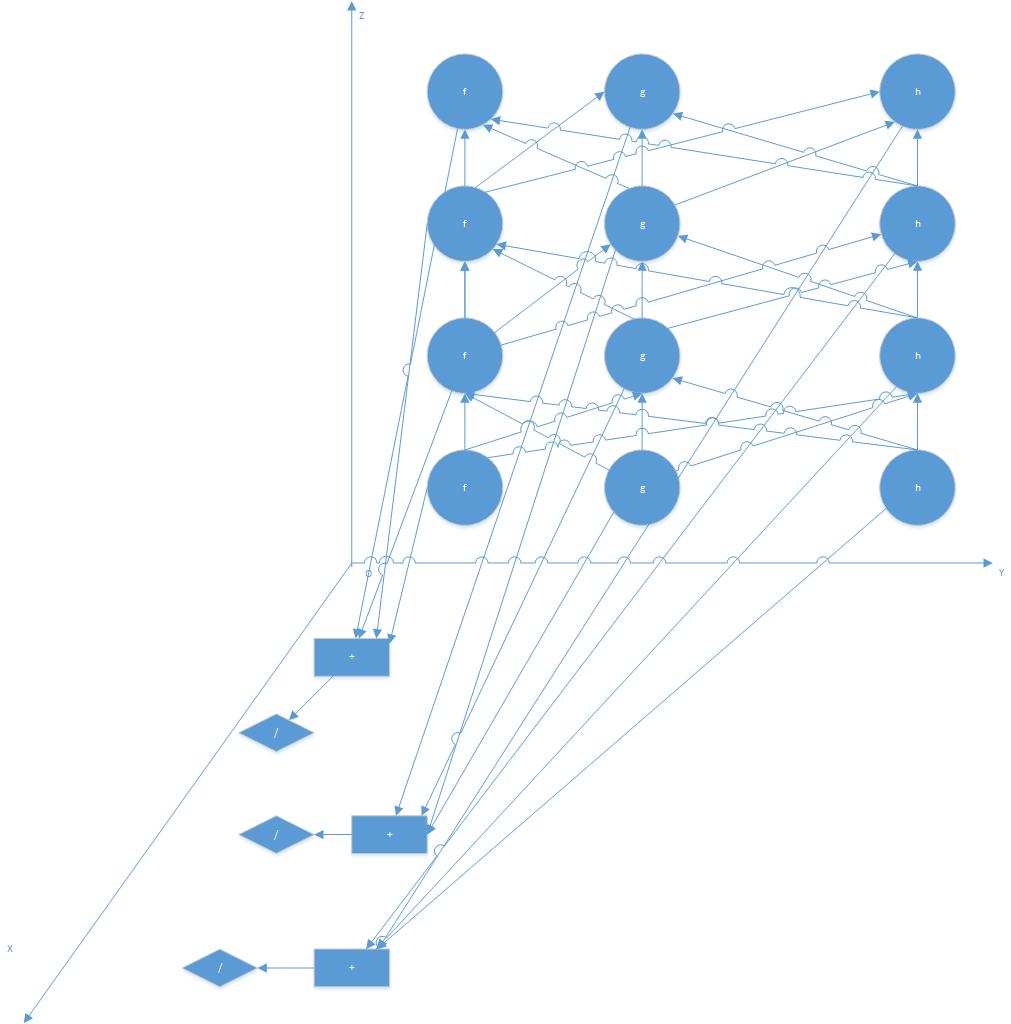
1.7 Информационный граф

Рисунок 1. Граф алгоритма

В плоскости Oyz происходит вычисление коэффициентов метода [math] k_1,k_2,k_3,k_4;m_1,m_2,m_3,m_4 [/math] и т.д. В плоскости Oxz происходит вычисление значений зависимых переменных [math] Y_{k+1} [/math] на очередном [math] k+1 [/math] шаге.

1.8 Ресурс параллелизма алгоритма

Для численного решения системы методом Рунге-Кутты в параллельном варианте требуется выполнить следующие ярусы (m-размер сетки, n-число уравнений):

1. [math] (3n+6)m [/math] ярусов сложений

2. [math] 4m [/math] ярусов умножений

3. [math] (3n+2)m [/math] ярусов делений

4. [math] 4m [/math] ярусов вычислений значения многомерной функции

Параллельная сложность алгоритма O(nm). Однако, не считая операций сложения, а также операций деления (в подавляющем большинстве это деление на 2), параллельная сложность будет равна O(m). То есть по сравнению с последовательным алгоритмом количество вычислений значения многомерной функции сокращается в n раз.

1.9 Входные и выходные данные алгоритма

Входные данные: вектор начальных данных размером n, вектор функций размером n

Выходные данные: матрица значений функций на каждом шаге сетки размером mn.

1.10 Свойства алгоритма

Параллельная версия алгоритма требует в n раз меньше операций умножения и вычислений значения многомерной функции. Особенностью алгоритма является то, что невозможно распараллелить вычисление значений зависимых переменных на каждом шаге сетки, так как алгоритм рекуррентный, то есть на каждом последующем шаге требуются данные с предыдущего.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – константа.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В простейшем варианте алгоритм можно записать на языке Delphi следующим образом:

unit RK_Method;

interface

type
        TVarsArray = array of Extended; // вектор переменных включая независимую
        TInitArray = array of Extended; // вектор начальных значений
        TFunArray = array of function(VarsArray: TVarsArray ):Extended;
        // вектор функций
        TResArray = array of array of Extended; // матрица результатов
        TCoefsArray = array of Extended; // вектор коэффициетов метода

function Runge_Kutt(  // метод Рунге-Кутта
        FunArray: TFunArray; // массив функций
        First: Extended; // начальная точка по независимой координате
        Last: Extended; // конечная точка по независимой координате
        Steps: Integer; // число шагов по независимой координате
        InitArray: TInitArray; // вектор начальных значений
        var Res: TResArray // матрица результатов включая независ. переменную
         ):Word; 
       // возвращаемое значение - код ошибки

implementation

Function Runge_Kutt(  // метод Рунге-Кутта
        FunArray: TFunArray; // массив функций
        First: Extended; // начальная точка по независимой координате
        Last: Extended; // конечная точка по независимой координате
        Steps: Integer; // число шагов по независимой координате
        InitArray: TInitArray; // вектор начальных значений
        var Res: TResArray // матрица результатов включая независ. переменную
         ):Word; // возвращаемое значение - код ошибки
var
        Num: Word; // число уравнений
        NumInit: Word; // число начальных условий
        Delt: Extended; // шаг разбиения
        Vars: TVarsArray; // вектор переменных включая независимую
        Vars2,Vars3,Vars4: TVarsArray; // значения перем. для 2-4 коэф.
        Coefs1: TCoefsArray; // вектор 1-ыx коэффициентов в методе
        Coefs2: TCoefsArray; // вектор 2 коэффициентов в методе
        Coefs3: TCoefsArray; // вектор 3 коэффициентов в методе
        Coefs4: TCoefsArray; // вектор 4 коэффициентов в методе
        I: Integer; // счетчик цикла по иттерациям
        J: Word; // индекс коэф.-тов метода
        K: Integer; // счетчик прочих циклов
begin
 Num:=Length(FunArray); // узнаем число уравнений
 NumInit:=Length(InitArray); // узнаем число начальных условий
 If NumInit<>Num then
   begin
     Result:=100; // код ошибки 100: число уравнений не равно числу нач. усл.
     Exit;
   end;
 Delt:=(Last-First)/Steps; // находим величину шага разбиений
 SetLength(Res,Num+1,Steps+1); // задаем размер матрицы ответов с незав. перем.
 SetLength(Vars,Num+1); // число переменных включая независимую
 SetLength(Vars2,Num+1); // число переменных для 2-го коэф. включая независимую
 SetLength(Vars3,Num+1); // число переменных для 3-го коэф. включая независимую
 SetLength(Vars4,Num+1); // число переменных для 4-го коэф. включая независимую
 SetLength(Coefs1,Num); // число 1-ыx коэф. метода по числу уравнений
 SetLength(Coefs2,Num); // число 2-ыx коэф. метода по числу уравнений
 SetLength(Coefs3,Num); // число 3-иx коэф. метода по числу уравнений
 SetLength(Coefs4,Num); // число 4-ыx коэф. метода по числу уравнений
 // Начальные значения переменных:
 Vars[0]:=First;
 For K:=0 to NumInit-1 do Vars[K+1]:=InitArray[K];
 For J:=0 to Num do Res[J,0]:=Vars[J]; // первая точка результата 
 For I:=0 to Steps-1 do // начало цикла иттераций
        begin
           For J:=0 to Num-1 do Coefs1[J]:=FunArray[J](Vars)*delt; // 1-й коэфф.
           // Находим значения переменных для второго коэф.
           Vars2[0]:=Vars[0]+delt/2;
           For K:=1 to Num do Vars2[K]:=Vars[K]+Coefs1[K-1]/2;
           For J:=0 to Num-1 do Coefs2[J]:=FunArray[J](Vars2)*delt; // 2-й коэф.
           // Находим значения переменных для третьго коэф.
           Vars3[0]:=Vars[0]+delt/2;
           For K:=1 to Num do Vars3[K]:=Vars[K]+Coefs2[K-1]/2;
           For J:=0 to Num-1 do Coefs3[J]:=FunArray[J](Vars3)*delt; // 3 коэфф.
           // Находим значения переменных для 4 коэф.
           Vars4[0]:=Vars[0]+delt;
           For K:=1 to Num do Vars4[K]:=Vars[K]+Coefs3[K-1];
           For J:=0 to Num-1 do Coefs4[J]:=FunArray[J](Vars4)*delt; // 4 коэфф.
           // Находим новые значения переменных включая независимую
           Vars[0]:=Vars[0]+delt;
           For K:=1 to Num do
           Vars[K]:=Vars[K]+
           (1/6)*(Coefs1[K-1]+2*(Coefs2[K-1]+Coefs3[K-1])+Coefs4[K-1]);
           // Результат  иттерации:
           For J:=0 to Num do Res[J,I+1]:=Vars[J];
        end; // конец итераций
 Result:=0; // код ошибки 0 - нет ошибок
end;

end.

2.4 Масштабируемость алгоритма и его реализации

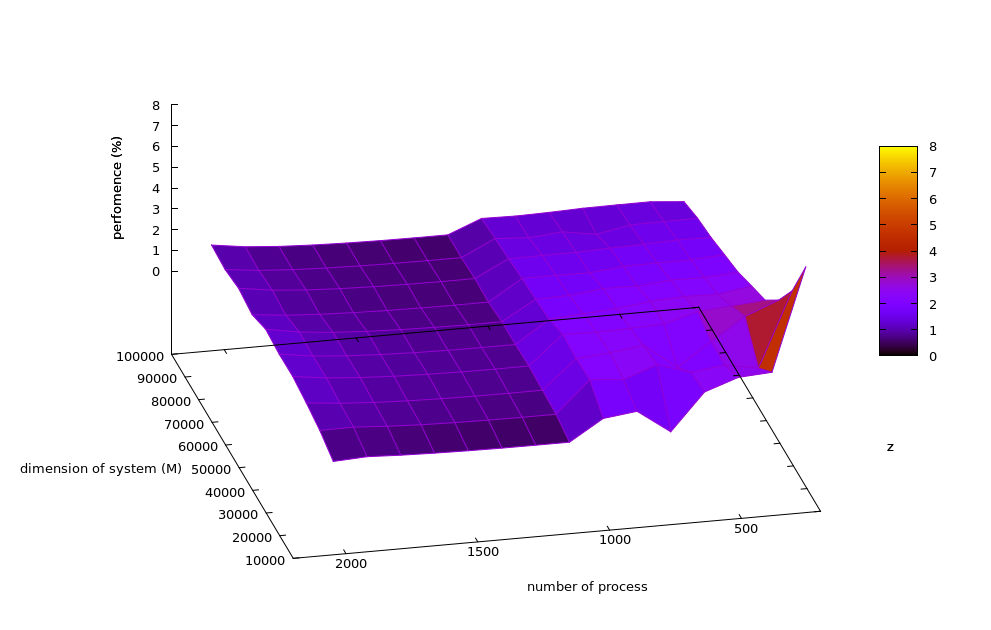
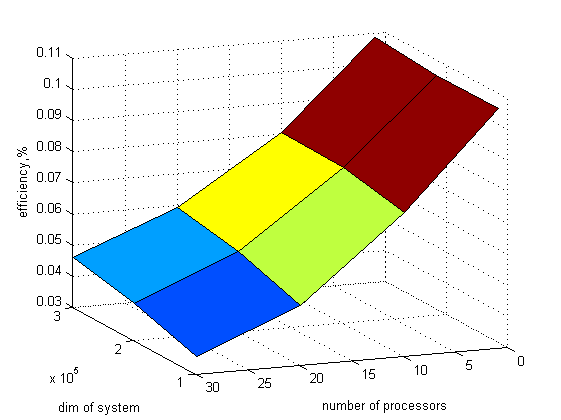
Запуск тестов производился на суперкомпьютере Ломоносов, на процессорах Intel Xeon X5670. Обсчет задачи производился на 1, 10, 20, 30 процессорах, размеры системы были 100000, 200000, 300000 уравнений. Использовался компилятор openmpi/1.8.4-gcc с опцией -fopenmp, библиотека OpenMPI версии 3.0.

На рисунке приведен график по производительности алгоритма и эффективности параллельной реализации

Рисунок 1

Рисунок 2

Исходя из графиков, можно сделать вывод, что производительность растет с увеличением числа процессоров, однако незначительно. Поэтому можно говорить о слабой масштабируемости. Максимальная эффективность достигается при использовании одного процессора - 0,1071%, минимальная при использовании 30 процессоров на матрице размера 100000 - 0,0355%. При увеличении размера задачи эффективность растет.

Использовалась реализация алгоритма, описанная в разделе 2.1.

2.7 Существующие реализации алгоритма

Алгоритм Рунге-Кутты 4-го порядка является одним из наиболее используемых для решения ОДУ и их систем, поэтому существует большое число его реализаций для разных языков программирования. Наиболее популярными являются следующие из них:

• библиотека RK4, которая существует в вариантах для C++, FORTRAN90, FORTRAN77, python и MATLAB;
• библиотека ode45 для MATLAB; Ссылка для скачивания https://www.mathworks.com/matlabcentral/fileexchange/41354-ordinary-differential-equation-toolbox--odebox-version-1-1#comments
• модуль scipy для PYTHON. Исходный код на github https://github.com/scipy/scipy

3 Литература

1. Н.С.Бахвалов, Н.П.Жидков, Г.М. Кобельков. Численные методы